有限元分析在船舶轴系设计中的应用
屠星星,徐勇杰
(上海船舶研究设计院,上海 201203)
有限元分析在船舶轴系设计中的应用
屠星星,徐勇杰
(上海船舶研究设计院,上海 201203)
使用 Abaqus 软件建立船舶轴系中间轴的模型,通过有限元方法计算轴法兰过渡处的应力集中系数,分析应力集中系数与轴系扭振计算结果之间的关系。相比于单圆弧过渡,三段式圆弧过渡将应力集中系数减小了20%,持续运转扭振许用应力提高了 38%,瞬时运转扭振许用应力提高了 17%。运用有限元分析方法检验校核了船舶轴系设计的合理性。
有限元分析;轴系设计;应力集中系数;扭振计算
0 引 言
船舶轴系是船舶动力装置的重要组成部分,承担着将主机发出的功率传递给螺旋桨以及将螺旋桨产生的推力传递给船体的重要任务。在对一型 37 000 DWT沥青船轴系的设计过程中,遇到了一个问题:其中间轴法兰过渡的原始设计是一个1/4圆弧,该情况下计算得到的扭振合成应力超过了瞬时运转的扭振许用应力,扭振计算无法获得通过。后采用三段式圆弧过渡形式,有效提高了扭振许用应力,扭振计算结果良好。鉴于轴系设计过程中,扭振合成应力超过许用限制的情况时有发生,且三段式圆弧过渡设计逐渐成为针对该问题的一种有效解决方法,有必要对法兰过渡形式与扭振计算结果之间的关系进行深入研究。
本文在轴系设计中引入有限元分析方法,以Abaqus 为工具,通过有限元方法计算中间轴法兰过渡处的应力集中系数,分析应力集中系数对扭振计算的影响,进一步阐述有限元方法之于轴系设计的意义。Abaqus 是一套功能强大的工程模拟的有限元软件,其解决问题的范围从相对简单的线性分析到许多复杂的非线性问题。 它前处理过程简便,适合用于中间轴之类简单模型的有限元分析[1]。
1 有限元分析计算
1.1简化模型
轴系包括从曲轴动力输出端法兰到螺旋桨间的轴及轴承,37 000 DWT 沥青船轴系如图1所示,中间轴位于主机和尾轴之间,将轴系以及螺旋桨和主机都进行建模是不现实的,有必要合理简化模型。理论应力集中系数主要受几何形状和加载方式等因素影响[2-3]与转速、振动的关系不大,所以本文在简化模型时去除了中间轴之外的部件[4]。同时因为理论应力集中系数受轴长度的影响很小,为了减小计算量,本文建模时将中间轴截断,只取一端进行建模分析[5]。
简化后的模型如图2所示。该三段式圆弧过渡的各参数公式为[6]:
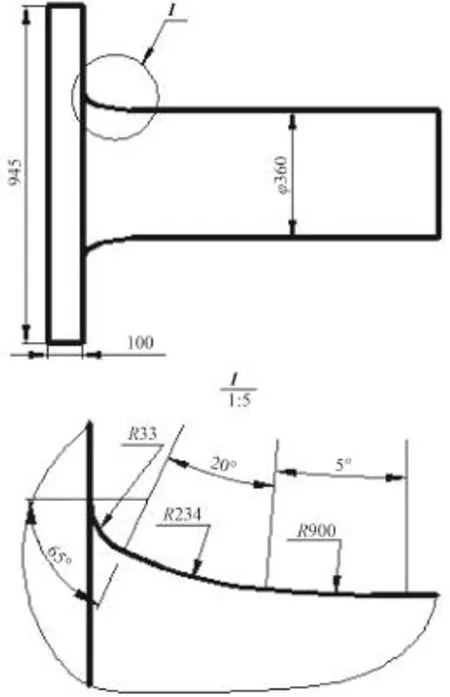
图2 中间轴模型Fig. 2 The intermediate shaft model

式中:D 为中间轴的直径;R1,R2和R3为三段圆弧的半径,θ1,θ2和θ3为三段圆弧对应的圆心角。
1.2生成三维模型,定义材料属性
图2是中间轴的二维平面模型,无法直接在Abaqus 中进行计算,需先转化成三维模型。首先将中间轴的 CAD 文件导入 Abaqus,通过旋转生成三维部件;其次创建一个新的材料,设置材料的属性(包括杨氏模量、泊松比、屈服应力等)。本船中间轴的材料为合金钢,在软件中将材料设置成各向同性,杨氏模量为206 GPa,泊松比为0.26,屈服应力为480 MPa。然后将该部件设置成均质实体,将材料属性赋予给该实体。
1.3定义边界,施加载荷
生成三维模型之后需定义模型左右两端的边界,将法兰左端完全固定,限制所有的平动和转动;对轴右端不设任何约束,使其完全自由。将扭矩施加于轴右端,理论应力集中系数与载荷大小无关,本文将扭矩设置成 1 000 Nm,方向是沿着 Y 轴。Abaqus 在施加扭矩时无法直接通过施加到一个点而传递到整个面。因此先将右端截面的圆心和整个面耦合起来,再将1 000 Nm 的扭矩施加到该圆心,使得圆心和整个截面的 6个自由度都运动一致[7]。
1.4划分网格,分析计算
采用四面体网格对中间轴模型进行划分,四面体网格能施加于任何几何体,且可以快速、自动生成。划分网格后的模型如图3所示。

图3 划分网格后的中间轴模型Fig. 3 The intermediate shaft model with finite element mesh
划分网格之后,即可建立作业进行计算。图4和图5分别是计算得到的单圆弧过渡和三段式圆弧过渡的切应力分布图。图6和图7分别是单圆弧过渡和三段式圆弧过渡的切应力分布剖面图。
计算结果表明,切应力是关于 Y 轴对称分布的。在同一个圆截面上,相同半径处的切应力大小相等,并且切应力随着半径的增大而增大,在轴的外沿切应力达到最大。在远离法兰的区域应力均匀分布;在过渡区域,出现了应力集中的现象,因此这个区域最容易被破坏。2种过渡形式应力集中导致的最大应力都出现在过渡弧与轴相切的位置附近,进一步的数据分析表明,最大应力出现在相切位置之前。
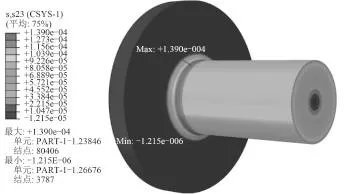
图4 单圆弧过渡的应力分布图Fig. 4 The stress distribution diagram of single radii transition
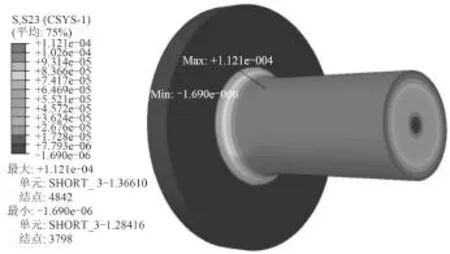
图5 三段式圆弧过渡的应力分布图Fig. 5 The stress distribution diagram of multi radii transition
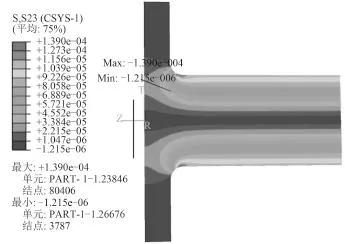
图6 单圆弧过渡的应力分布剖面图Fig. 6 The sectional view of stress distribution of single radii transition

图7 三段式圆弧过渡的应力分布剖面图Fig. 7 The sectional view of stress distribution of multi radii transition
三段式圆弧过渡设计产生的最大切应力为1.121 05 × 10-4GPa,单圆弧过渡设计产生的最大切应力为1.390 04 × 10-4GPa,三段式圆弧过渡设计明显降低了应力集中程度,有效减小了最大切应力。同时对于理论应力集中系数,它是最大局部应力与名义应力的比值,名义应力是未发生应力集中时的应力。
名义切应力的理论计算为:
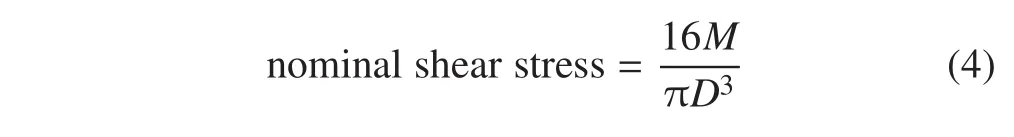
式中:施加的扭矩 M=1 000 Nm;中间轴轴径 D=360 mm,代入上式得到名义切应力 nomina shear stress=109 160 Pa。
应力集中系数 scf(stress concentration factor)计算如下:
三段式圆弧过渡
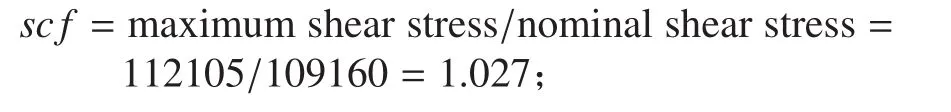
单圆弧过渡
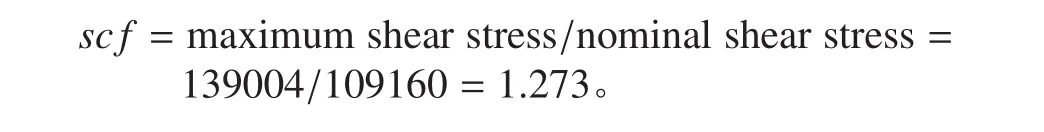
与单圆弧过渡相比,三段式圆弧过渡将应力集中系数减小了近 20%,把应力集中降低到了相当小的程度。进一步的建模研究表明,三段式圆弧过渡的应力集中系数大小主要取决于与轴相切的那段弧的半径,也就是取决于 R1的大小。在前 2 段弧过渡未出现明显突变的情况下,R1越大,应力集中系数越小。目前,R1=2.5 D 的设计已经足以获得理想的应力集中系数。对于单圆弧过渡形式,同样可以采取扩大过渡半径的方法来减小应力集中系数,但单圆弧的过渡半径受到法兰半径的限制,很难获得与三段式圆弧过渡那样好的效果。
2 扭振分析
中国船级社《钢质海船入级规范》中轴系振动与校中章节对中间轴的扭振许用应力做了如下规定:
持续运转(0 < r < 0.9):

CW为材料系数,
Rm为轴材料的抗拉强度,本船中间轴的 Rm=800 MPa;
CD为尺度系数;D 的单位是 mm;
根据规范规定,对于三段式圆弧过渡(理论应力集中系数为1.027,保守取值为1.05):
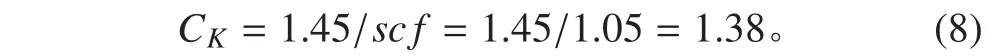
单圆弧过渡的 CK计算并不采用以上公式,而是为了安全起见,将CK默认为1.0[8]。
式(5)~式(7)表明,持续运转和瞬时运转的扭振许用应力随着转速的增大而减小。另外,持续运转和瞬时运转的扭振许用应力都随着 CK的增大而增大,而 CK随着 scf 的减小而增大,这就意味着扭振许用应力是随着应力集中系数的减小而增大的。因此,对于1 根已经成形的中间轴,其扭振许用应力只与转速相关;然而在设计阶段,可以在一定程度内通过改变法兰过渡的应力集中系数来控制扭振许用应力的大小。
图8为37 000 DWT 沥青船采用单圆弧过渡的中间轴扭振计算结果。图8表明,单圆弧过渡的情况下,在 48 r/min 转速附近,计算得到的扭振合成应力超过了瞬时运转扭振许用应力,这是不允许的。
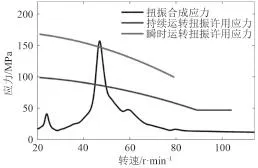
图8 单圆弧过渡的扭振计算结果Fig. 8 The torsional vibration calculation of single radii transition
图9为37 000 DWT 沥青船采用三段式圆弧过渡的中间轴扭振计算结果。图9表明,当采用三段式圆弧过渡之后,持续运转扭振许用应力提高了 38%,瞬时运转扭振许用应力提高了约 17%,2 条扭振许用应力曲线都往上移动了。因此,扭振合成应力的最大值被控制在瞬时运转扭振许用应力之内。转速为47.6 r/min时,扭振合成应力最大,且超过了持续运转扭振许用应力,这个转速的附近是转速禁区。转速禁区范围计算公式如下:

图9 三段式圆弧过渡的扭振计算结果Fig. 9 The torsional vibration calculation of multi radii transition
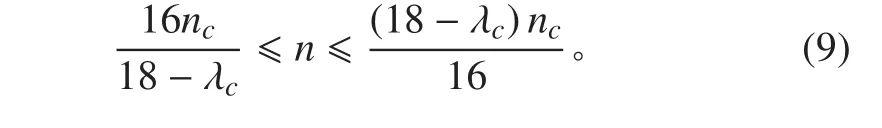
式中:nc为出现峰值应力时的转速,即 47.6 r/min;λc为nc的比值。
计算得到转速禁区在 43 r/min 与 52 r/min 之间,在转速禁区内应快速通过,不得持续运转。
综上所述,三段式圆弧过渡的设计通过降低应力集中系数提高了许用应力,有效地将扭振合成应力控制在许用范围之内,确保中间轴安全运转。三段式圆弧过渡设计避免了额外增设扭振减振器,降低了37 000 DWT 沥青船的成本。
3 结 语
本文将有限元分析方法应用于船舶轴系设计之中,计算了单圆弧过渡和三段式圆弧过渡的应力集中系数,详细分析了应力集中系数与扭振计算结果之间的关系。
有限元分析方法在船舶轴系设计中的应用,一方面便于直接检验校核轴系设计的合理性,另一方面有助于为复杂轴系设计提供解决方案。
[1]张玉峰, 朱以文, 丁宇明. 有限元分析系统Abaqus中的特征技术[J]. 工程图学学报, 2006, 27(5): 142-148. ZHANG Yu-feng, ZHU Yi-wen, DING Yu-ming. Feature technology of finite element analysis system Abaqus[J]. Journal ofEngineering Graphics, 2006, 27(5): 142-148.
[2]雷继军, 韩致信. 异形截面轴肩的应力集中特征[J]. 兰州理工大学学报, 2010, 36(4): 44-47. LEI Ji-jun, HAN Zhi-xin. Stress concentration character at shaft shoulder with abnormal cross-section[J]. Journal of Lanzhou University of Technology, 2010, 36(4): 44-47.
[3]陈科, 殷磊, 陈振华. 万向十字轴轴根过渡结构的优化设计和分析[J]. 中国机械工程, 2014, 25(23): 3155-3159. CHEN Ke, YIN Lei, CHEN Zhen-hua. Optimization and analysis of transition curves for roots of universal cross shaft[J]. China Mechanical Engineering, 2014, 25(23): 3155-3159.
[4]吴凤林, 任家骏. 轴肩过渡曲线形状设计研究[J]. 中国机械工程, 1998, 9(9): 15-16. WU Feng-lin, REN Jia-jun. Research on shape design of shoulder transition curve[J]. China Mechanical Engineering,1998, 9(9): 15-16.
[5]NISITANI H, NODA N A. Stress concentration of a cylindrical bar with a V-shaped circumferential groove under torsion, tension or bending[J]. Engineering Fracture Mechanics, 1984,20(5/6): 743-766.
[6]Det Norske Veritas AS. Calculation of shafts in marine applications[R]. Classification Notes No. 41.4. Norway: Norway Classification Society Press, 2013: 18-19.
[7]符芮三. ABAQUS与PERFORM-3D在弹塑性时程分析中的应用及对比研究[D]. 重庆: 重庆大学, 2014. FU Rui-san. The application and comparation of ABAQUS and PERFORM 3D in elastic-plastic time history analysis[D]. Chongqing: Chongqing University, 2014.
[8]中国船级社. 钢质海船入级规范[M]. 北京: 人民交通育出版社, 2014: 257-258. China Classification Society. Rules for classification of sea-going steel ships[M]. Beijing: China Communications Press, 2014:257-258.
Application of finite element analysis in marine shaft design
TU Xing-xing, XU Yong-jie
(Shanghai Merchant Ship Design and Research Institute, Shanghai 201203, China)
The intermediate shaft was modeled by ABAQUS and the stress concentration factor was calculated with method of finite element analysis. And it analyzed the relationship between the stress concentration factor and the torsional vibration calculation. Compared to single radii transition, Multi radii transition reduced the stress concentration factor by 20 percent. meanwhile, the torsional vibration allowable stress value in continuous operation mode was increased by 38 percent and that in instantaneous operation mode was increased by 17 percent. The finite element analysis checked the rationality of the marine shaft design.
finite element analysis;shaft design;stress concentration factor;torsional vibration calculation
U664.121
A
1672-7619(2016)09-0087-05
10.3404/j.issn.1672-7619.2016.09.017
2016-02-25;
2016-04-13
屠星星(1990-),男,硕士,助理工程师,从事轮机设计工作。

