船舶低频纯横荡及纯首摇运动数值仿真与分析

李冬琴，徐士友，刘存杰

（1. 江苏科技大学 船舶与海洋工程学院，江苏　镇江 212003；2. 江苏现代造船技术有限公司，江苏　镇江 212003）

船舶低频纯横荡及纯首摇运动数值仿真与分析

李冬琴1，2，徐士友1，刘存杰1

（1. 江苏科技大学 船舶与海洋工程学院，江苏镇江 212003；2. 江苏现代造船技术有限公司，江苏镇江 212003）

以船舶操纵水动力预报为研究背景，利用商用软件 Fine/Marine 对 DTMB5415 进行了低频纯横荡及纯首摇运动数值仿真研究。以纯横荡运动幅值为0.064 m 试验数据为基准，通过对比不同边界条件设置及其对计算结果的影响分析，得到随体坐标系下船模受到的侧向力及转首力矩，并将仿真计算结果与船模试验结果进行对比，获得较好的参数设置。以该设置参数及边界条件为依据进行后续的纯横荡运动及纯首摇运动数值仿真计算，得到船模所受侧向力及转首力矩。

纯横荡；纯首摇；网格划分

0　引　言

在传统的船舶设计中，操纵性相较于船舶快速性和耐波性是次要考虑因素，然而船舶操纵性是关系到航行安全的一个重要因素，随着 IMO（International Maritime Organization）对操纵性标准的提高，船舶操纵性受到越来越多的关注［1］。自航模或约束模试验是预报操纵性最可靠的方法，然而船模试验需要特定的实验设备，且船模试验存在实验周期较长、实验费用高昂及尺度效应无法消除的缺点。

基于计算流体动力学（Computational Fluid Dynamic， CFD）技术的数值模拟方法是近年来出现的最先进的船舶操纵预报方法，该方法通过离散求解非定常操纵运动方程，得到相关船舶运动参数和运动轨迹，从而实现用纯数值计算的方法对船舶操纵性进行理论预报。与船模试验相比，数值仿真计算具有计算费用少、计算周期短，而且能够获得局部流动状态信息的优点。随着计算机技术的发展，CFD 技术在操纵性领域从最初的定常运动仿真发展至现在用于非定常运动仿真［2-4］。本文以 DTMB5415 为仿真对象，以横荡幅值为0.064m 的试验数据为基准［5］，设置不同边界条件进行数值仿真计算，对计算结果进行分析得到最佳边界条件设置。然后基于小振幅假设对低频率纯横荡及纯首摇运动进行数值仿真计算，求解船舶操纵相关的粘性流动，得到满意流体水动力以及水动力矩。

1　运动数学模型

1）纯横荡运动

船模匀速前进的同时叠加一个横向正弦规律变化的位移［6-7］。

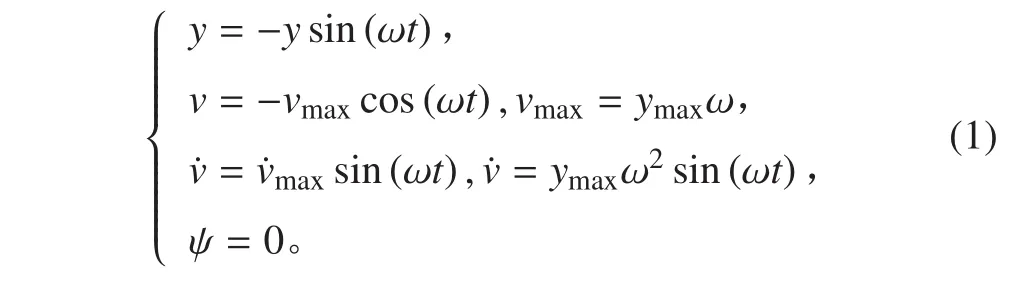
式中：ymax为横荡运动幅值；ω为横荡运动频率；ν为横荡运动速度；为横荡运动加速度。

由于本文研究的是小振幅横荡运动，线性假设下船模进行纯横荡运动时所受的水动力和水动力力矩可表示为：

将式（1）和式（2）合并有：

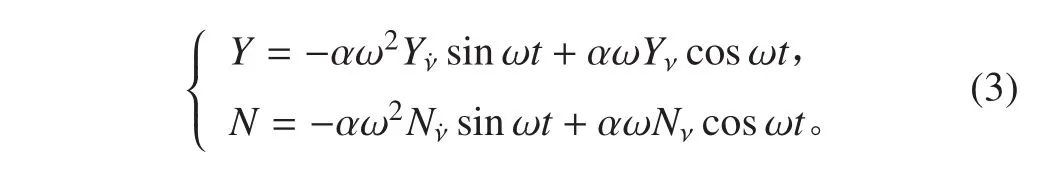
由式（3）可知，只要测得船舶横荡运动过程中所受的侧向力及转首力矩就可以获得四个水动力导数。

2）纯首摇运动

船模保持匀速前进的同时首向角进行正弦规律变化［6-7］。船模运动轨迹时刻与纵轴保持相切。运动规律为：

式中：ψmax为首向角幅值；ω 为首摇运动频率；r 为首摇运动角速度；为首摇运动角加速度。

由于本文研究的是小振幅首摇运动，线性假设下船模进行纯首摇运动时所受的水动力和水动力力矩可表示为：

合并式（4）和式（5）有：

由式（6）可知，只要测得船舶首摇运动过程中所受的侧向力及转首力矩就可以获得四个水动力导数。

2　数值仿真计算

1）网格划分

本文以 DTMB5415 为对象进行数值仿真计算［8］，缩尺比为1∶46.588。几何模型如图1所示。

图1　DTMB5415 几何模型Fig.1　The geometry of DTMB5415

在数值仿真计算过程中，计算域的划分对计算结果的精确度与计算时长都密切相关。计算域过大，会使得网格数目增多，造成计算资源浪费；计算域划分过小，会产生浅水效应和岸壁效应，使数值模拟与真实的运动状态不同［9］。文中计算域划分如图2所示。

图2　计算域划分Fig. 2　Division of computational domain

网格质量是影响数值仿真计算的可行性、收敛性和计算精度的主要因素。在进行网格划分时考虑到船体表面曲率变化较大，需进行局部加密，同时对自由液面进行加密，以便捕捉液面的变化。网格划分完成以后需对网格质量进行检查，所划分的网格不能包含负体积及凹体积，负体积是无效的计算单元，凹体积将影响计算稳定性，同时推荐网格正交性大于 5。

2）CFD 边界条件设置

对纯横荡运动进行 3种不同幅值的低频运动仿真；纯首摇运动进行 3种不同首向角的低频运动仿真。计算工况见表1。

图3中 Slip、Wall 代表数值仿真计算过程中甲板设置为滑移壁面条件和壁面函数条件，Exp 代表试验值。滑移壁面条件应用于壁面切向速度为0，壁面函数法主要适用于低雷诺数层流流动。图3为2种边界条件下的数值仿真计算结果与实验数据拟合图形。

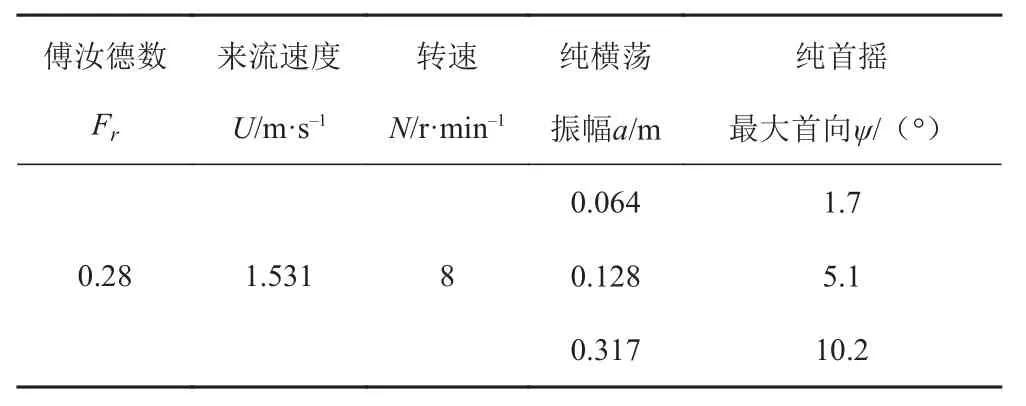
表1　计算工况Tab.1　The condition of the simulation

图3　纯横荡运动船模受到侧向力及转首力矩Fig. 3　Lateral force and moment of pure swaymotion

甲板边界设置为滑移壁面时，数值仿真结果与试验数据之间相对误差均值为0.25%，甲板采用壁面函数时，数值仿真结果与试验数据之间相对误差均值为0.45%。从计算结果来看，考虑空气粘性影响后，数值计算结果较之前计算值略有变大，增大幅度不超过0.5%。但考虑空气粘性影响后，网格需在滑移壁面网格基础上进行加密处理，从节省计算资源及提高效率的角度出发，本文后续仿真计算，忽略甲板空气粘性的影响，甲板的边界条件采用滑移边界条件。

图4中 bottom_pres 及 bottom_far 分别表示流域下壁面边界条件为指定压力边界（Prescribed Pressure）和远场边界（Far Field）条件，Exp 代表试验值。远场边界条件是通过速度分量的大小初始化边界上的速度，所给定的速度方向取决于具体的流动状态。指定压力边界条件属于 Dirichlet 条件，在计算初始化过程中指定边界压力。通过图4可以发现：底部壁面设置为指定压力时，数值仿真计算结果与试验值吻合度较好，二者之间的平均相对误差为8.75%；底部壁面设置为速度远场时的数值仿真计算结果已经无法用于实际工程。

图4　纯横荡运动船模受到侧向力及转首力矩Fig. 4　Lateral force and moment of pure swaymotion

综上，对不同边界条件设置得到的计算结果进行分析可知，空气密度较小，甲板设置为滑移壁面或壁面函数时，2种边界条件下的数值仿真计算结果与试验数据之间的相对误差均较小。为充分利用计算资源，本文进行后续数值仿真计算过程中甲板采用滑移壁面边界；流域底部壁面设置为远场边界条件时的数值仿真计算结果已无法用于实际工程，而流域底部壁面设置为指定压力时，数值仿真计算结果与试验数据之间相对误差较小。因此，在后续数值仿真计算过程中为了得到理想结果，甲板边界选择滑移壁面边界，流域底部壁面需选取指定压力边界条件。

3）纯横荡运动

纯横荡运动是通过船模恒定速度（U=1.531 m/s）前进，同时沿横向叠加正弦规律变化的位移实现。为了便于将数值仿真计算结果与试验数据进行对比，数值仿真计算过程中设置水温与试验水温保持一致，设置为13.5 ℃，流体特性参照 ITTC 推荐值进行设置，横荡运动幅值分别为0.064 m，0.128 m，0.317 m。

图5中 Sim 0.064 等分别代表不同横荡幅值下一个周期内数值仿真计算结果，Exp0.064 等分别代表不同横荡幅值下一个周期内试验值。船模试验与数值仿真计算最大、最小值及相对误差见表2。采用本文介绍的 CFD 设置及网格划分，计算出的最大误差为-20.9%，最小误差为-0.5%，本文计算结果相比于参考文献，纯横荡的侧向力及转首力矩的相对误差有一定的改善。考虑到船体形状和运动的复杂性，这样的误差在可以接受的范围内。而误差的来源可能是：数值仿真计算中忽略了运动过程中产生的兴波；实验过程中没有限制纵倾和升沉运动，然而数值仿真过程中没有考虑这 2种运动。

图5　纯横荡运动船模受到侧向力及转首力矩Fig. 5　Lateral force and moment of pure sway motion

表2　数值仿真计算结果与船模试验结果对比Tab. 2　Ship model numerical results with experimental results compare

4）纯首摇运动

纯首摇运动是通过船模以1.531 m/s 的速度匀速前进，同时船模绕铅直轴进行正弦规律变化的运动实现的。运动过程中船模合速度与船模的中纵剖面始终相切。为了便于将数值仿真计算结果与试验数据进行对比，设置水温为13.5 ℃，流体特性参照 ITTC 推荐值设置，首摇运动首向角幅值分别为1.7°，5.1°，10.2°

图6中 Sim1.7 等分别代表不同横荡幅值下一个周期内数值仿真计算结果，Exp1.7 等分别代表不同首向角下一个周期内试验数据。船模试验与数值仿真计算最大值、最小值及相对误差见表3。数值仿真计算结果与船模试验数据最大相对误差为27.5%，最小相对误差-0.88%。考虑到船体形状和运动的复杂性，这样的误差在可以接受的范围内。而误差的来源可能是：数值仿真计算中忽略了运动过程中产生的兴波；实验过程中没有限制纵倾和升沉运动，然而数值仿真过程中没有考虑这 2种运动。

图6　纯首摇运动船模受到侧向力及转首力矩Fig. 6　Lateral force and moment of pure yaw motion

3　结　语

本文利用商用软件 Fine/Marine 以 DTMB5415 为模型对纯横荡运动的一种工况试验数据为基准，采用不同边界条件进行数值仿真计算，分析边界条件对数值仿真计算结果的影响，从中找出适宜的边界条件进行纯横荡运动及纯首摇运动仿真。将纯横荡运动及纯首摇运动数值仿真计算结果与实验数值结果进行对比，数值仿真计算与船模试验结果曲线吻合较好。考虑船型的复杂及局部信息处理的不全面性以及数值仿真计算过程中忽略自由兴波的影响，计算结果在可接受范围内。本文数值仿真计算计算得到相对误差总体相对参考文献相对误差有一定改善，从而说明本文在网格划分及边界条件设定符合本文数值仿真计算要求。

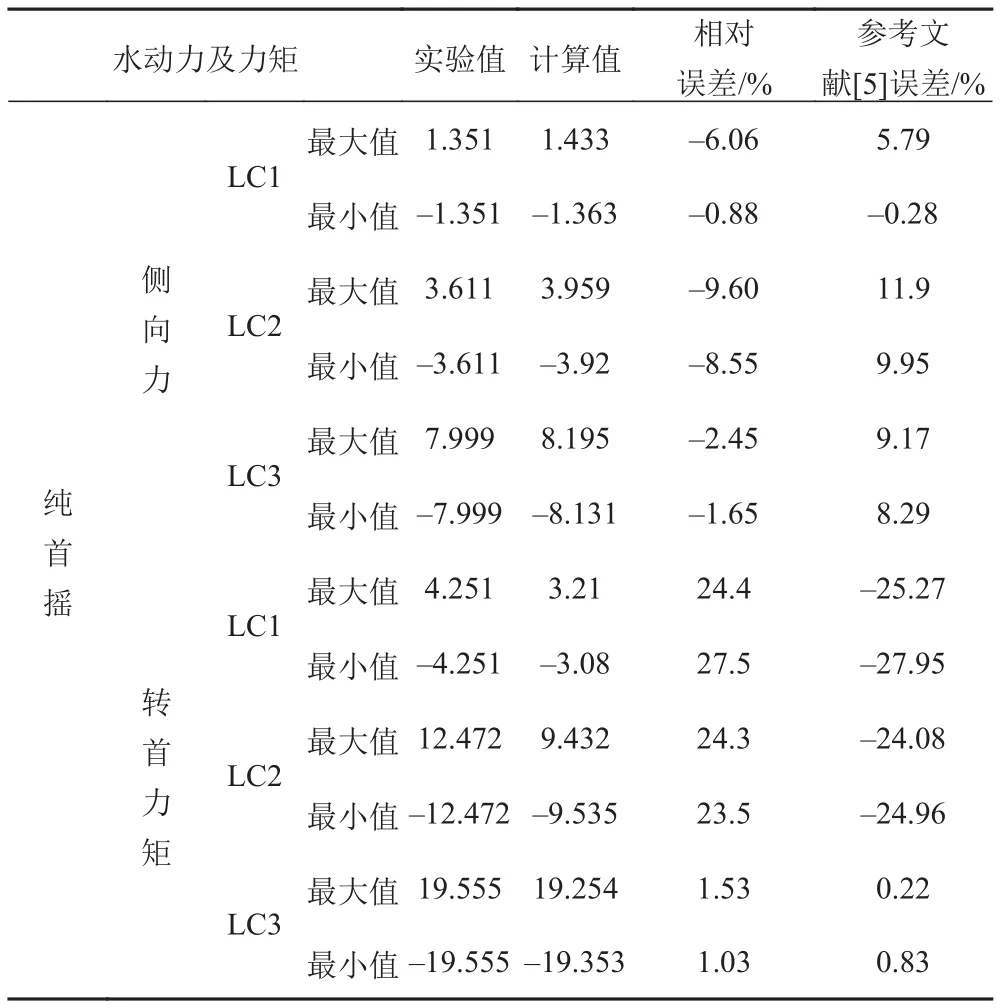
表3　数值仿真计算结果与船模试验结果对比Tab. 3　Ship model numerical results with experimental results compare

［1］YOON H， SIMONSEN C D， BENEDETTI L， et al. Benchmark CFD validation data for surface combatant 5415 in PMM maneuvers-part I： force/moment/motion measurements［J］. Ocean Engineering， 2015，109： 705-734.

［2］田喜民， 邹早建， 王化明. KVLCC2船模斜航运动粘性流场及水动力数值计算［J］. 船舶力学， 2010，14（8）： 834-840. TIAN Xi-min， ZOU Zao-jian， WANG Hua-ming. Computation of the viscous flow and hydrodynamic forces on a KVLCC2 model in oblique motion［J］. Journal of Ship Mechanics， 2010，14（8）： 834-840.

［3］SIMONSEN C D， STERN F， AGDRUP K. CFD with PMM test validation for manoeuvring VLCC2 tanker in deep and shallow water［C］//Proceedings of International Conference on Marine Simulation and Ship Maneuvering （MARSIM）. Terschelling， the Netherlands： MARSIM， 2006.

［4］LIU H， MA N， GU X. Maneuvering prediction of a VLCC model based on CFD simulation for PMM tests by using a circulating water channel［C］//ASME 201534th international conference on Ocean， Offshore and Arctic Engineering. St. John's，Newfoundland， Canada： The American Society of Mechanical Engineers， 2015.

［5］刘山. 基于CFD技术数值模拟平面运动机构试验［D］. 武汉： 武汉理工大学， 2012. LIU Shan. Numerical simulation of planar motion mechanism test based on CFD technology［D］. Wuhan： Wuhan University of Technology， 2012.

［6］吴秀恒， 刘祖源， 施生达， 等. 船舶操纵性［M］. 北京： 国防工业出版社， 2005. WU Xiu-heng， LIU Zu-yuan， SHI Sheng-da， et al. Ship maneuverability［M］. Beijing： National Defence Industry Press，2005.

［7］范尚雍. 船舶操纵性［M］. 北京： 国防工业出版社，1988. FAN Shang-yong. Ship Maneuverability［M］. Beijing： National Defence Industry Press，1988.

［8］http：//www.simman2008.dk

［9］郭然， 贾力平， 樊小莉， 等. NUMECA系列教程［M］. 北京： 机械工业出版社， 2013. GUO Ran， JIA Li-ping， FAN Xiao-li， et al. NUMECA series tutorial［M］. Beijing： Machinery Industry Press， 2013.

Ship low-frequency pure sway and pure yaw motion numerical simulation and analysis

LI Dong-qin1，2， XU Shi-you1， LIU Cun-jie1
（1. School of Naval Architecture and Ocean Engineering， Jiangsu University of Science and Technology， Zhenjiang 212003， China；2. Jiangsu Modern Shipbuilding Technology， Ltd.， Zhenjiang 212003， China）

In order to predict the shipmaneuverability in viscous flows， using commercial software Fine/Marine for DTMB5415 of low-frequency pure sway and pure yawmotion simulation， obtained the lateral force and yaw moment which fixed on the ship model.A condition test data of pure sway as a benchmark， by comparing different boundary conditions and their impact on the results， obtainthe lateral force and torque， the simulation results with the ship model test results were compared to obtain better parameter settings.In this setting the parameters and boundary conditions as a basis for subsequent pure swaying motion and pure yaw motion numerical simulation， get boats suffered a lateral force and torque under this setting.

pure sway；pure yaw；meshing

U662

A

1672-7619（2016）09-0009-05

10.3404/j.issn.1672-7619.2016.09.002

2015-12-07；

2016-05-31

国家自然科学基金资助项目（51509114）；江苏省科技成果转化专项资金资助项目（BA2015042）；江苏高校高技术船舶协同创新中心/江苏科技大学海洋装备研究院资助项目（HZ2016015）

李冬琴（1979-），女，博士，副教授，从事多学科设计优化方法及现代船舶设计方法研究。