一种基于LSA与FCM的文本聚类算法
王文霞
(运城学院计算机科学与技术系,山西运城044000)
一种基于LSA与FCM的文本聚类算法
王文霞
(运城学院计算机科学与技术系,山西运城044000)
在文本聚类中,基于向量空间模型(VSM)的文本特征空间存在高维度和稀疏空间、同义词与多义词干扰等问题;而K-means算法依赖于初始聚类中心,聚类结果随不同的初始输入而有所波动。针对这些问题,本文提出了一种基于潜在语义分析(LSA)与优化的模糊C均值(FCM)的文本聚类算法——LF。该算法首先采用一种新的词特征提取方法建立词-文本矩阵;然后对该词-文本矩阵进行奇异值分解在潜在语义空间进行降维;接着用优化的模糊C均值聚类算法实现对文本的聚类分析。最后通过实验,结果表明LF算法能更好地改善了文本聚类的结果,提高了文本的查全率和查准率。
文本聚类;FCM;LSA;遗传优化;k-means算法
近年来随着互联网的发展与普及,各种信息呈爆炸式的增长。在这海量的文本信息中如何快速、准确地挖掘出有价值的、用户感兴趣的信息,是当前计算机信息理论研究的重点和热点。其中,文本聚类作为数据挖掘的重要分支之一,不需要预先设定文本类别,也不需要训练过程,自动化处理能力较高且具有一定的灵活性,在信息检索、信息过滤、数字化图书馆、搜索引擎等很多领域都有着广阔的应用前景。
目前,对文本的聚类分析,通常是基于向量空间模型(VSM)的文本表示法和K-means聚类算法实现对文本的聚类分析。VSM的文本表示法将文本用词语向量表示出来,对应为空间中的点,并通过计算空间中两点间的距离获得文本之间的相似度,进而基于经典的K-means聚类方法实现对文本的聚类[1-2]。但是VSM存在着两大缺点:(1)当文本比较长时,词汇量就会变得很大,这往往会产生高维的文本向量,使得很多传统算法难以处理;(2)VSM中对于词语权重的计算主要是基于统计的,只考虑文本中关键词出现的次数,而不考虑关键词在上下文语境中的语义,忽略同义词与多义词的干扰,往往使得聚类结果不准确。K-means聚类算法是一种基于划分的聚类算法,其基本思想是不断迭代更新直至目标函数取得极小值,从而取得最优聚类效果。但是,该算法依赖于初始聚类中心的选定,分类的个数K也需事先确定,且种子选取的好坏都直接影响着文本聚类的效果,进而影响文本的检索质量。
因此,本文提出了一种LF:基于LSA和FCM的文本聚类算法。该算法首先采用LSA模型来代替传统的VSM,再用模糊C均值对文本进行聚类,最后用遗传算法优化聚类结果。该算法不仅可压缩问题规模,而且聚类结果又用遗传算法进行全局最优化处理,使得聚类分析在时间性能和质量上都能获得较好的效果。
1 LSA模型
1.1 LSA的基本思想
潜在语义分析(LSA)模型是1990年S T Dumais等人提出了一种新的信息检索代数模型。LSA的基本思想是首先构造一个包含m个文本和n个词的文本集的词汇-文本矩阵A,再基于数学中的奇异值分解(SVD)理论对矩阵A进行分解得到A=USVT。其中,U是一个m*m的正交矩阵,其列为矩阵A的左奇异值向量;V是一个n*n的正交矩阵。其列为A的右奇异值向量;S为对角矩阵,其元素称为A的奇异值[3]。假设A的秩为r,通过取U的前k(k<=r)列,V的前k行,以及S中的前k个奇异值可得Ak=UkSkVkT,这样就可以很好解决传统向量空间模型所存在的问题,实现:(1)通过奇异值分解大大降低向量空间的维数;(2)A k是原矩阵A在k维子空间上最小二乘意义上的最佳近似,应用于信息的分解和重构,可以提取有用信息,消除噪声,实现语义检索[4]。
为了实现文本的聚类,需要获得文本与文本间的相似度。LSA模型表示文本后,便可以求得词语与词语之间的相似度、文本与文本之间以及词语与文本之间的相似度。本文中采用向量间的余弦值来计算文本间相似的的方法,文本Di与Dj之间的相似度用如下公式求得:
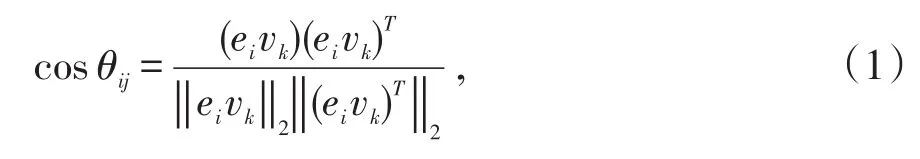
其中,表示k阶单位矩阵的第i列。
1.2 新的特征权重算法
在传统的特征权重计算方法TF-IDF中,只考虑了同一文本中词的出现频率和包括某次的文本数,并没考虑其他因素。而实际上由于不同词在文本中的作用不同,对文本的重要程度也不同。因此,在构造词-文本矩阵时往往要考虑该因素对不同的词赋予不同权重。本文对传统的TF-IDF特征选择算法进行了改进,增加了对词的熵权重这个因素的考虑。
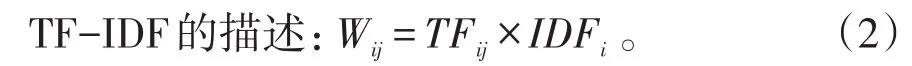
基于信息理论,提出的熵权重是一种最复杂的权重计算方法,其计算方法为:
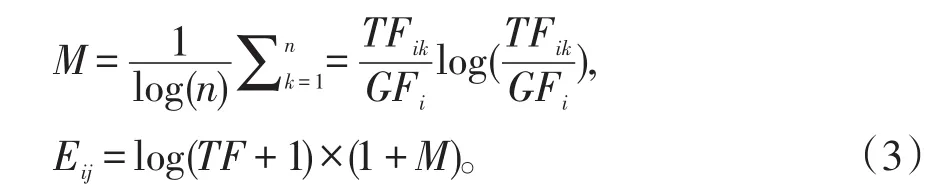
其中,M表示特征词i的平均熵。
本文中,将两者结合起来,给出了一种新的特征权重计算法,其计算公式为:

2 优化的FCM算法
2.1 FCM的基本思想
模糊C均值(FCM)算法[5]的基本思想是基于某种准则,把没有类别标记的样本集划分为若干子集,使相似的样本尽可能划分到一类,而把不相似的样本归于不同的类中。传统的K-means聚类分析是一种硬划分,把每个样本严格划分到某类中,但这与实际不符,因为现实中大多数待分类样本并没有严格分界限,在各种特征上都存有一定中介性。FCM就是用模糊的方法进行聚类分析,是对样本类别的不确定描述,从而更客观的反应世界;且该算法思想简单、收敛速度快,便于处理大规模数据且易于计算机实现,因而成为了聚类分析的主流算法[6]。
FCM实现的具体步骤如下:
Step 1:在[0,1]间取随机数来初始化隶属矩阵U(1),需满足一个数据集的隶属度的和总等于1,即初始化迭代截至误差a(a>0)。
Step 2:计算聚类中心Ci,i=1,…,c,
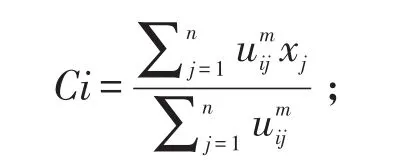
Step 3:计算价值函数。若计算结果小于某个给定的阀值,或相对改变量小于另一个给定的阀值,则聚类分析结束。

Step 4:计算新的U矩阵。返回步骤2,直到

但是,FCM算法性能依赖于初始聚类中心,其容易陷入局部极值点;且得到的结果是模糊的,仍需确定化。因此,本文基于遗传算法对FCM算法进行了优化,其基本思想是从文本集中随机抽样选取文本,应用FCM算法,获取模糊聚类结果;再以该结果作为遗传算法的初始群体,进行优化处理,从而输出最优聚类解[7]。
2.2 遗传算法进行聚类优化
FCM算法的计算过程是迭代的,一次迭代很容易陷入局部极值点,从而得不到最优解。本文基于遗传算法对FCM算法进行了优化,其基本思想是从文本集中随机抽样选取文本,应用FCM算法获取模糊聚类结果,再以该结果作为遗传算法的初始群体,进行优化处理,从而输出最优聚类解。
假设文本聚类结果C={c1,c2,…,ck}是通过模糊C均值聚类算法得到的,其中聚类的个数表示为k。用遗传算法进行聚类优化过程的详细步骤如下所示:
Step 1:染色体编码和初始群体的产生。本文采用二进制编码方式对染色体进行编码,其编码长度设定为聚类个数k;同时,随机会产生Psize个长度为k的二进制编码染色体作为初始群体(Psize为种群规模)。
Step 2:适应度评估。在该算法中对染色体适应度的评估分为两步:新聚类的创建和适应度的计算。
随机选择一个染色体S创建新聚类,其聚类过程为:
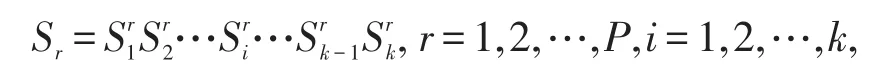
适应度的计算用于评估聚类的质量,本文采用了误差平方和准则函数JC来进行适应度评估,其定义为:
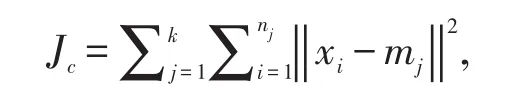
其中,xi代表文本集中的文本向量;nj代表第j个类中含有的文本数。Jc的值越小,说明类内相似度就越高,聚类质量越好;反之Jc的值越大,聚类质量越差。
Step 3:遗传操作主要包括选择、交叉和变异三个部分。
选择:选择是从当前群体中选取优良个体,适应度越大的个体被选取的概率就越高,使其有机会作为父代繁殖下代。本文采用了轮盘赌选择法(也就是适应度比例法)来进行个体的选择。假定第i个染色体的适应度值为fi,那么i被选中的概率可用下面公式计算可得:

交叉:交叉操作体现了信息交换的思想,将原来的优良基因遗传给下一代,生成更复杂基因结构的个体。一般采用的交叉方式有一点交叉、两点交叉、多点交叉、一致交叉等。这里,采用两点交叉并按照一定的交叉概率PC来产生新个体,取PC的值为0.80。
变异:变异操作可反映出群体的多样性。这里,对其变异值采取“非”操作,并取变异概率PM的值为0.010。
步骤4:算法终止。以满足最大迭代数或者保持种群中最优个体适应度持续30代不变作为算法的终止条件。
3 LF算法
LF算法是LSA文本表示模型与优化的FCM算法结合的文本聚类算法,首先采用一种新的特征权重计算建立词-文本矩阵,同时对该词-文本矩阵进行奇异值分解,并用文本语义向量的余弦来表示文本之间的相似度;然后用优化的模糊C均值(FCM)对上述计算文本相似度的结果进行聚类分析。
LF算法的步骤如下:
Step 1:输入原始文本集,语义空间的维数为K,模糊加权指数b;
Step 2:采用公式(3)构造词-文本矩阵A;
Step 3:基于LSA模型对矩阵A进行奇异值的分解,构建原始文本集的潜在语义空间为Ak;
Step 4:将文本向量映射成为语义空间Ak中语义向量,并计算文本之间的相似度;
Step 5:实现文本聚类,采用FCM算法计算出各类的聚类中心以及相应的隶属度值;
Step 6:去除模糊聚类结果的模糊化,把模糊聚类变为确定性分类;
Step 7:用遗传算法对上述的聚类结果进行优化。
4 实验结果及分析
本文实验的文本集来自某门户网站1100个页面,从中提取了1000个文本,这些文本被主题分为:经济、军事、政治、教育、科技和体育。定义了三个评估指标,查准率p(Precision)、查全率r(Recall)和F-Score[7]。查准率p代表了类别C中的文本在实际相符的文本中所占的比例;查全率r则代表专家判定属于类别C的文本中,聚类后被正确归类的文本所占的比例;F-Score方法代表综合评价聚类结果,F-Score定义如下:
本文采用LF算法和K-means算法进行聚类,并对它们的结果进行比较,如图1所示为其实验结果。从图1中可以看出,采用LF算法对文本进行聚类时,其查准率、查全率以及F-Score系数均高于k-means算法。故LF算法通过引入优化策略能够很好地改善文本聚类的效果,聚类结果的准确度比较高,同时能有效地克服向量空间模型存在的弊端。
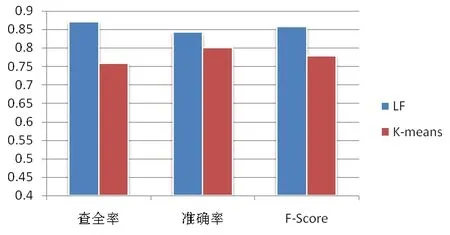
图1 LF算法与K-means算法聚类结果比较
图2和图3是LF算法在K和b分别取不同值时的文本聚类结果统计。由图可知,聚类的准确性受到语义空间维数K的影响,当选取的K值太小,文本集中留下来的语义信息将太少,从而导致区分文本的能力不足;反之,当选取的K值太大时,就失去了LSA模型的优势,接近于向量空间模型,失去其降维、降噪的能力。因此,文本聚类时要选取的K值要合适,这样使得文本聚类准确度达到最高。同时,模糊加权指数b对聚类准确度也有一定影响,如b取2时比b取1时的聚类结果要好。

图2 LF在不同语义空间维数K和b=1聚类结果
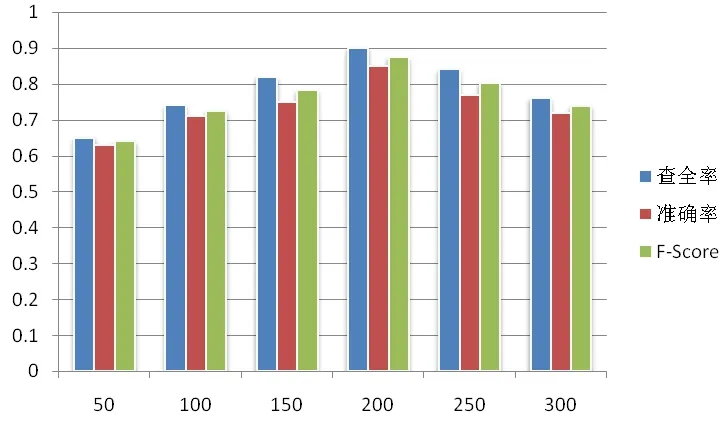
图3 LF在不同语义空间维数K和b=2的聚类结果
5 总结
针对传统向量空间模型在文本聚类过程中所存在的高维稀疏性,无法解决同义词、多义词问题,K-means算法需要预定聚类个数和依赖于初始聚类中心的弊端。本文提出的文本聚类算法,采用了潜在语义分析以及优化的模糊C均值,实现了高维文本向量的降维处理,降低了文本处理的复杂度;同时采用了模糊C均值算法对文本进行聚类,简单且收敛速度又快,并用遗传算法对聚类的结果进行优化。通过实验验证,LF算法能更好地改善了文本聚类的结果,提高了文本的查全率和查准率。LSA算法是基于统计的方法,尽管优化的LSA算法考虑了词的熵权重,它并没有词在文本中上下文环境,但是上下文环境对文本语义有着非同寻常的意义。在将来的工作中,把词在文本中上下文环境考虑进来,以将聚类的准确度进一步提高。
[1]任姚鹏,陈立潮,张英俊,等.结合语义的特征权重计算方法研究[J].计算机工程与设计,2010,31(10):2381-2383.
[2]胡永丽,龚沛曾.基于模糊C均值和改进的LSA的文档聚类研究[J].计算机技术与发展,2010,20(12):126-129.
[3]俞辉.基于改进LSA的文本聚类算法[J].小型微型计算机系统,2009,30(5):963-966.
[4]LANDAUER T K,FOLTZ P W,LAHAM D.Introduction to latent semantic analysis[J].Discourse Processes,1998,27(25):259-284.
[5]李雷,罗红旗,丁亚丽.一种改进的模糊C均值聚类算法[J].计算机技术与发展,2009,19(12):71-73.
[6]DUNN J C.Well-separated clusters and the optimal fuzzy partition[J].Journal of Cybernetic,1974(4):95-104.
[7]张英俊,任姚鹏,陈立潮,等.基于语义相似度与优化的构件聚类算法[J].计算机工程与设计,2010,31(11):2531-2535.
The Text Clustering Algorithm Based on LSA and FCM
WANG Wen-xia
(Department of Computer Science and Technology,Yuncheng University,Yuncheng Shanxi,044000)
The text clustering based on Vector Space Model has problems,such as high-dimensional and sparse,unable to solve synonym and polyseme etc.And meanwhile,k-means clustering algorithm has shortcomings,which depends on the initial clustering center and needs to fix the number of clusters in advance.Aiming at these problems,in this paper,a text clustering algorithm based on Latent Semantic Analysis and Improvded fuzzy C-means is proposed——LF.The algorithm first uses a new feature extraction method for establishing the word-text matrix;then the word-text by singular value decomposition of the matrix and the latent semantic space dimensionality reduction for text semantic vectors;then using fuzzy C means on the text of the similarity calculation results clustering,genetic algorithm is used to optimize clustering result.our algorithm is proved which can preferably improve the effect of text clustering,and upgrade the precision ratio and recall ration of text.
text clustering;FCM;LSA;genetic optimization;k-means clustering algorithm
TP311
A
1674-0874(2016)01-0008-04
2015-08-24
运城学院教学改革研究项目[JG201418]
王文霞(1979-),女,山西运城人,硕士,讲师,研究方向:数据挖掘及算法分析。
〔责任编辑 高海〕

