无指定相交圈的非负特征图的列表点荫度

张海辉

（淮阴师范学院数学科学学院，江苏淮安 223300）

无指定相交圈的非负特征图的列表点荫度

张海辉

（淮阴师范学院数学科学学院，江苏淮安 223300）

对于图的任一顶点集的划分，并使每个划分的导出子图均为无圈图的最小的划分基数称为图的顶点荫度.对于图G的每个顶点给定一个列表基数至少为k的颜色集合，对于图的任一染色，若每个顶点的颜色均选择与其关联的颜色集，使得每种颜色类的导出子图是一个无圈图的最小的基数k称为图的列表点荫度.证明了每个无6圈和相交i，j-圈（i，j∈｛3，4｝）的非负特征图的列表顶点荫度为2，即为4列表可选色.

非负特征图；荫度；选色

0　引言

文中所考虑的图都是有限、简单图.G=（V，E，F）表示一个图，V（G），E（G），F（G）分别为其顶点集，边集和面集.若uv∈E（G），则称u，v在G中相邻.若u是边e的一个端点，则称顶点u与这条边e相关联.若两个面至少有一条公共边，则这两个面称为是相邻的.一个面f边界记为b（f），任何面f与b（f）上所有顶点及边都相关联.v的邻集NG（v）（即G中与v相邻的顶点集）中元素的个数即为顶点v的度数.

称图G的使得每个顶点划分的导出子图均为无圈图的最小的划分基数称为图的顶点荫度，记为ρ（G）.用等价的图的顶点染色可以重述为：称图的一个无圈的k着色为从顶点到集合｛1，2，…，k｝的一个映射，使得满足每个颜色类的导出子图是一个无圈图.图的顶点荫度即为使得图有一个无圈k着色的最小的整数k.

1968年Chartrand等人提出图的荫度又称为图的点荫度［1］并证明了对于任何图G，有ρ（G）≤且当G为平面图时，有ρ（G）≤3；Chartrand等人［2］证明了如果G为外平面图时，有ρ（G）≤2.1975年Kronk和Mitchenm在文［3］中给了一个类似Brook定理形式的顶点荫度结论：如G为奇数个顶点的图，且即不是圈也不是完全图，则有

Raspaud等证明了每个不含3圈或4圈或5圈或6圈或不含距离小于2的三角形的平面图的点荫度为2［4］.2012年Huang等证明了不含7圈的平面图点荫度为2［5］.Chen等人证明了每个不含相交三角形的平面图的点荫度为2［6］.Choi等人证明了每个不含4圈的轮胎图是顶点2可荫度的［7］.

对G中所有顶点v∈V（G）的一个颜色安排，使得每个顶点能从其关联的色表中选色并且相邻的两个顶点选择不同的颜色称为G的一个L-着色.若对图G的每个满足L=｛L（v）‖L（v）|=k，v∈V（G）｝的着色安排，图G总存在L-着色，则称图G是k-可选色.定义使得图G是k-可选色的最小的自然数k为图G的选色数，记为ch（G）.列表染色的概念由Vizing和Erdos Erdos分别在文［8］和［9］中引出.在2000年Borodin等人将顶点荫度和列表染色的概念融合［10］，介绍了列表顶点荫度的概念.

对于图G的每个顶点给定一个列表基数至少为k的颜色集合，对于图的任一染色，若每个顶点的颜色均选择于其关联的颜色集，使得每种颜色类的导出子图是一个无圈图的最小的基数k称为图的列表点荫度.记为ρl（G）.Xue等人给出二部图的列表荫度可以任意大［11］.在2008年Borodin等证明每个三角形距离小于2的图是列表2可荫度的［12］.在2009年Borodin等人又证明了无4圈相邻3圈的平面图也是列表2可荫度的［13］.Zhen和Wu证明若一个图的顶点荫度足够接近于图的顶点数的一半［14］，则ρl（G）=ρ（G）.

若图G的任一子图均含有一个度至多为k的顶点，则称图G为k退化的.Raspaud和Wang证明对任何k退化图，有Xue和Wu证明此结论对于列表顶点荫度也成立，即文中研究了非负特征图的列表顶点荫度.对任何可2胞腔嵌入在曲面S的图G而言，曲面S的特征值等于|V（G）|+|F（G）|-|E（G）|.欧几里得平面，仿射平面，轮胎图，克莱茵瓶都是带有非负特征值的曲面.整篇文章中，我们称一个非负特征值的图为NC-图.

设＄表示无6圈和相交i，j-圈（i，j∈｛3，4｝）的NC-图.我们讨论了＄中图的列表点荫度.在第1部分，介绍了相关的一些概念定义.第2部分，我们给出了此类图的一个结构定理.作为引理1的一个推论，得到了定理1的证明.

引理1 设图G是一个非负特征图，若图G不含6圈和相交i，j-圈（i，j∈｛3，4｝），则有δ（G）≤3.

定理1 任何不含6圈和相交i，j-圈（i，j∈｛3，4｝）的非负特征值图G的列表点荫度小于等于2.

推论1 任何不含6圈和相交i，j-圈（i，j∈｛3，4｝）的非负特征值图G是4可选色的.

1　定义和概念

度数为k的顶点称为k-顶点.若r≤k或1≤k≤r，此时k-顶点分别称之为r+-或r--顶点.G中顶点的最大与最小度分别记为Δ（G），δ（G）.与f关联的边的数目（割边按2次算）记为面f的度数，记作dG（f）.若dG（f）=k，则f叫做k-面.若r≤k或3≤k≤r，则k-面f分别称之为r+-或r--面.有k个顶点的圈称为k-圈.G中所有k-圈的集记为Ck.若Ck=φ，则称图G是Ck-free的.G中最短圈的长度称为G的围长.f∈F（G），如u1，u2，u3，…，um按时针方向在面f的边界上，记f=［u1u2u3…un］.对一个n-面f，如果f=［u1u2u3…um］，且d（ui）=mi（i=1，2，…，n），则称为（m1，m2，m3，…，mn）-面.

若面的边界形成一个圈，一个面f称为是一个简单的面.显然，当最小度大于等于2时，且面的长度小于5时，或者对任一2连通的图，每一个面都是简单面.

若x∈V（G）∪F（G），用nk（x）表示和x相关联或邻接的度为k的顶点的集合，用mk（x）表示和x相关联或邻接的长度为k的面的集合.

2　引理1的证明

证 设G为＄中一个满足条件的阶最小的反例，有G不含6圈，且无相交3圈，相交的4圈，和相交的3圈和4圈，并且δ（G）≥4.

若某个顶点在一个面上出现2次，则称这个面f为节俭的.显然，由于不含6圈，＄中的任意图G所含的6面必定是节俭的.任何两个面如果只有一条边在其公共边界上，则称为正常相邻.否则称为非正常相邻，即两个面至少有3个公共的顶点.

首先给出证明引理1所需要的一些结构性的结论：

断言1 图G不含相邻的3面和5面.

证 设f为一个3面，且b（f）=［v1v2v3］.f1为一个5面，且b（f1）=［v1v2u1u2u3］.除非v3∈｛u1，u2，u3｝，否则v3v2u1u2u3v1v3将形成一个6圈，与题意不符.但是若v3=u1，则d（v2）=2，与最小度要求矛盾.若v3=u2，则出现相交的3圈.由对称性可知，v3≠u3，得证.

断言2 图G不存在6面.

证 若G含有6面，则必定为一个节俭的6面，否则与无6圈相矛盾此时出现了相交的三角形，矛盾.

断言3 对图G的任一顶点v，有m4-（v）≤1.

对于任一v∈V（G）给一个列表安排使得|L（v）|=4，由守恒定理，权值的总和是-4l.为了证明引理1，下面介给出一条简单的权电荷移动方案，根据方案，由于权电荷的移动始终在图的内部在相互转换，因此整个图的权值应是始终不变，即始终是小于等于0的.然而，一旦根据移动规则进行操作后，文中证明移动之后的权值w*不是小于等于零，而是大于0，则就与权值不变形成一个矛盾，这样，就能完成引理1的证明.

权的移动根据以下规则，对于任意的x∈V（G）∪F（G）

从每个5+-x到每个关联的4--面，

令v是图G的一个k-顶点：当k=4时，由（R）w*（v）=w（v）=0；当k≥5时，由断言3可知，

令f是图G的一个k-面.当k=3时，由断言1及断言2有f与3个7+-面相邻.从每个5+-x到每个关联的4--面，有w*（f）≥w（f）＞0.当k=4时.由图的属性及移电荷规则，f与4个5+-面相邻.从而有w*（f）≥w（f）·4＞0.当k≥5时，由断言3、断言4及规则（R）有

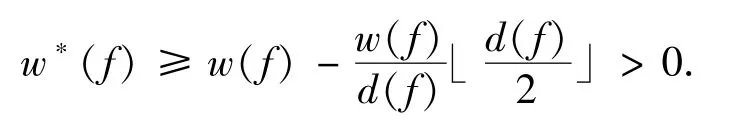
这样证得了对所有的x∈V（G）∪F（G），w*（x）≥0，有

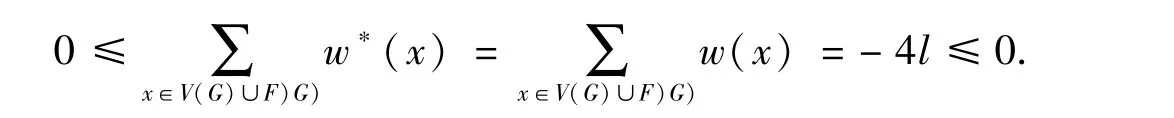
断言5 图G为空图.

证 由上述证明过程可知，对于图的所有的面，在运用电荷规则转移后，面权均大于零.故图不存在面，图为空图.

断言5的成立与图的最小度条件相矛盾，得证.

3　定理1的证明

证 由引理1可知，＄中的图类均为3退化的，由退化图的列表点荫度的结论可知，＄中的图G均有定理1得证.

［1］ Chartrand G，Kronk H V，Wall C E.The point-arboricity of a graph［J］.Israel J Math，1968，6（1）：169-175.

［2］ Chartrand G，Kronk H V.The point-arboricity of planar graphs［J］.J Lond Math Soc，1969，44（1）：612-616.

［3］ Kronk H V，Mitchem J.Critical point-arboritic graphs［J］.J Lond Math Soc，1975，9（2）：459-466.

［4］ Raspaud A，Wang W.On the vertex-arboricity of planar graphs［J］.European J Combin，2008，29（4）：1064-1075.

［5］ Huang D，Shi W C，Wang W.On the vertex-arboricity of planar graphs without 7-cycles［J］.Discrete Math，2012，312（15）：2304-2315.

［6］ Chen M，Raspaud A，Wang W.Vertex-arboricity of planar graphs without intersecting triangles［J］.European J Combin，2012，33（5）：905-923.

［7］ Choi I，Zhang H.Vertex arboricity of toroidal graphs with a forbidden cycle［J］.Discrete Math，2014，333（28）：101-105.

［8］ Vizing V G.Coloring the vertices of a graph in prescribed colors［J］.Metody Diskret Anal，1976，29（1）：3-10.

［9］ Erdos P，Rubin A L，Taylor H.Choosability in graphs［J］.Graph Theory Computing，Congr Numer，1980，26（1）：125-157.

［10］ Borodin O V，Kostochka A V，Toft B.Variable degeneracy：extension of Brook's and Gallai's theorems［J］.Discrete Math，2000，214（2）：101-112.

［11］ Xue N，Wu B.List point arboricity of graphs［J］.Discrete Math Algorithms Appl，2012，4（2）：1-10.

［12］ Borodin O V，Ivanova A O.List 2-arboricity of planar graphs with no triangles at distance less that two［J］.Siberian Electronic Math Reports，2008，5（2）：211-214.

［13］ Borodin O V，Ivanova A O.Planar graphs without 4-cycles adjacent to 3-cycles are list vertex 2-arborable［J］.J Graph Theory，2009，62（3）：234-240.

［14］ Zhen L，Wu B.List point arboricity of dense graphs［J］.Graphs Combin，2009，25（1）：123-128.

On list Vertex Arboricity of Graphs with Nonnegative Characteristic without Cycles of Specific Length

ZHANG Hai-hui
（Department of Mathematics，Huaiyin Normal University，Huaian Jiangsu 223300，China）

The vertex arboricity ρ（G）of a graph G is the minimum number of subsets into which vertex set V（G）can be partitioned so that each subset induces an acyclic graph.A graph G is called list vertex k-arborable if for any sets L（v）of cardinality at least k at each vertex v of G，one can choose a color for each v from its list L（v）so that the subgraph induced by every color class is a forest.The smallest k for a graph to be list vertex k-arborable is denoted by ρl（G）.We prove that any graph with nonnegative characteristic without cycles of intersecting cycles i，j-cycles for i，j∉｛3，4｝has ρl（G）≤2 and is 4-choosable.

graphs with nonnegative characteristic；arboricity；choosability

O157.5

A

1671-6876（2016）03-0189-04

［责任编辑：李春红］

2016-04-12

国家自然科学基金资助项目（11501235）；国家自然科学基金天元基金资助项目（11226285）；江苏省自然科学基金资助项目（BK20140451）；江苏省高校自然科学基金资助项目（15KJB110002）

张海辉（1979-），男，江苏泰兴人，副教授，博士，主要从事图论与组合数学研究.E-mail：hhzh@hytc.edu.cn