基于空气动力学N-S方程的正方体绕流问题研究

刘　璐

(西安航空学院 飞行器学院，陕西 西安 710077)



基于空气动力学N-S方程的正方体绕流问题研究

刘璐

(西安航空学院 飞行器学院，陕西 西安 710077)

绕流是一个经典的空气动力学问题，对于涡流的产生和形成一直是教学过程中的难点。通过对流体绕过正方体的研究，可以具体地展示出涡流随时间产生和发展，帮助理解涡流的形成过程和规律。首先对动量方程进行分析推导，得到压力泊松方程，使用交错网格投影法将N-S方程离散化，并得到离散化的压力泊松方程，通过使用SOR技术来求解。利用MATLAB建模，根据所得到的图像来具体分析流体绕过正方体的特征。结果显示流体从正方体的一角分离、卷起并在正方体后方立即形成一对反向旋涡，该反向漩涡随即分解，后形成几个分散的漩涡，形象地展示了涡流随时间变化的过程。

N-S方程；正方体绕流；数值仿真

正方体是一种典型的钝头柱体，关于正方体绕流问题的研究一直是空气动力学领域的热点问题之一，比如在大型建筑物、冷却塔、热交换器等等方面[1]。这是因为空气绕过固体表面物体产生和脱落的涡流会影响物体上被施加的载荷，如果分离频率接近于物体的自激震荡频率，可能会使物体损坏[2]。

绕流现象是一类现实生活广泛存在的空气动力学问题。由于流体流过结构时会产生分离现象，结构会受到持续力的作用，因而产生周期性震动，可能会使结构产生疲劳等现象。近年来，关于绕流现象的研究一直不断。得益于计算机速度的提高和计算方法的发展，数值模拟成为研究绕流问题的重要方法。王亚玲等利用不可压缩N-S方程，模拟了不可压缩流体的圆柱体绕流问题[3]。马金花等利用有限元方法求解雷诺平均N-S方程，对圆柱体绕流问题进行数值模拟[4]。但他们采用N-S方程的求解方法是流函数-涡量法，引入流函数，连续方程自动满足；然后让u动量方程和v动量方程分别对y和x求偏导，消掉压力项，并利用涡量-速度的关系式合并相关速度项，就能得到涡量方程；同样，再利用流函数-速度-涡量关系可得流函数的Poisson方程，这样，原方程就简化为了求流函数和涡量两个变量的方程。这种方法相对于SOR法较简单，不需要假设-迭代，但是边界条件的处理尤其关键，当边界条件简单的情况下，这种方法有效。但当绕流固体为正方体时，流函数-涡量法计算较慢，还可能会出现不收敛的情况。

本文应用MATLAB代码定义正方体与流体接触面，然后将边界条件应用于N-S方程，再使用交错网格投影法，经过迭代求解N-S方程，从而得到不同时间下的涡线图。

1　N-S方程及求解方法

N-S方程，即纳维-斯托克斯方程。本文中N-S方程是针对二维非定常不可压缩流体绕过正方体的研究，方程具体形式如下所示：

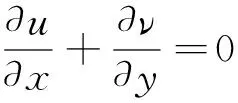
(1)

(2)

(3)

其中，u和v是速度在两个方向上的分量，p是压力，而Re是雷诺数[5]。

本文采用的N-S方程求解方法为压力泊松方程法。这种方法的核心还是迭代，先将u动量方程与v动量方程分别对x和y求偏导，然后相加，并利用连续方程合并相关项，这样就得到了压力泊松方程。先不需要考虑压力，而是从动量方程得到一个中间速度，然后把此速度代入泊松方程，用泊松方程代替连续方程，这样可以得到一个关于两个方程的迭代式[6]。

2　泊松方程的求解方法

在本文中，使用逐次超松弛法来解泊松方程。逐次超松弛法(successive over relaxation method)，简称SOR方法[7]，是解线性方程组的常用迭代法之一，它由高斯-赛德尔迭代法经线性加速处理而得到[8]。原理如下：

假设方程组Ax=b的系数矩阵AX=b

(4)

A是n×n的矩阵 元素从a11到ann

(5)

使用下面的迭代格式来建立解方程组Ax=b的逐次超松弛迭代法(SOR)。

(6)

这里引入ω，ω为松弛因子，其定义如下：

(7)

nx和ny是网格上x方向和y方向上格子的数目，这会比用传统的高斯-赛德尔迭代法求解线性方程时拥有更快的趋同速率[9]。

3　计算步骤

使用MATLAM软件进行求解：

(1)定义任意几何形状的图形：创建主体形态，在定义域内定义固体表面X、Y方向的数值，正方体的边长为2。

(2)参数的定义和初始化变量：确定雷诺数和时间步长，选取雷诺数为100，时间步长为0.1。

(3)找到主体的指数：将从可变形状中指定主体的位置转换到u,v和p的储存位置。

(4)检查稳定性标准：之前定义的时间步长将通过稳定性的标准来验证。

(5)设置域边界的速度边界条件。

(6)设置主体的速度边界条件：首先将主体内全部速度点设置为零，然后从先前定义过的参数信息中寻找所需要的边界条件的位置。

(7)求解表面上的u和v：使用循环计算表面上u和v的临时值。

(8)在n+1的时间阶上求解压力：用泊松算法求解离散泊松方程。

(9)求解u和v：在n+1的时间阶上的速度分量是使用循环来计算出的。循环包含了除主体内的所有速度点。

(10)设置压力边界条件：对计算域和主体边界施加针对压力的离散形式的诺依曼条件。

(11)更新t和呈现结果：时间自动跳过一个时间步长直到时间已经超过开始时设置的最大时间，然后绘制出涡线图。

4　计算结果及分析

设置正方体的边长为2，气流的雷诺数Re=100，在固体表面u=v=0，时间步长为0.1。然后采用MATLAB软件计算t分别在10，50，100s时的正方体绕流瞬时涡线，如图1～图3所示。

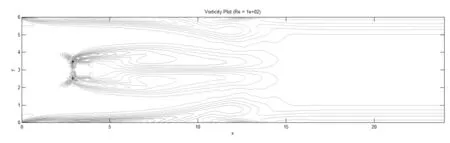
图1t=10s的瞬时涡线

图2　t=50s的瞬时涡线

图3　t=100s的瞬时涡线

图中显示了在t=10s，50s，100s时单位正方体绕流的瞬时涡线，这个正方体被放置在上下对称的区域范围内，距离入口L=0.5。在入口处，指定了一个简单均匀的速度，随后流量在到达主体之前得到充分发展。当雷诺数为100时，数值解可以由不均匀的细小网格求得。结果表明，下游流量是不稳定的；流量从主体脱离后，在主体后形成旋涡。在第一个10s，交叉流从主体的一角分离、卷起并在主体后立即形成一对反向旋涡，如图1所示。然后反向漩涡开始分解，随后形成几个分散的漩涡，如图2和图3所示。在t=100s后，形成非对称稳定涡旋。

气流在正方体前部发生分离，一部分是因为物体的阻碍作用，另一部分是因为气流与固体表面有粘性力作用，消耗了流体的动能，使得气流不能沿固体表面流动，从而发生了气流分离。而在正方体的后方形成了一定的低压区内，不稳定气流形成了涡旋，随着时间的增长，涡旋也不断地发展、分解，最后形成分散的非对称涡旋。

5　结语

本文应用投影网格交错法，求解了在二维定常流动下，雷诺数为100时，流体绕过正方体后，在t=10s，50s，100s时，涡流形成的情况，与实验结果较为吻合。今后可以将MATLAB应用于求解流体绕过任意形状物体的过程，以及任意气流条件下的绕流，可以更加深入了解涡流形成的过程，以减少涡流的形成和影响，可以发现更加方便计算和收敛N-S方程的数值方法。

[1] 刘宇，苏中地.不同雷诺数下方柱绕流的数值模拟[J].中国计量学院学报，2006，17(1)：40-49

[2] 谢志刚，徐春晓，崔桂香，等.方柱绕流大涡模拟[J].计算物理，2007,24(2)：171-180.

[3] 王亚玲，刘应中，缪国平.圆柱绕流的三维数值模拟[J].上海交通大学学报，2001，35(10)：1464-1469.

[4] 马金花，金生，贺德馨，等.圆柱体绕流的数值模拟[J].山东建筑工程学院学报，2001，16(2):45-47.

[5] 王建，金志浩，张玉娇.方柱绕流的数值模拟[J].沈阳化工学院学报，2007，21(2)：117-120.

[6] 景思睿，张鸣远.流体力学[M].西安：西安交通大学出版社，2001:210-211.

[7] Woodward P,Colella P.The Numerical Simulation of Two-dimensional Fluid Flow with Strong Shocks[J].Journal of Computational Physics,1984,54(1):115-173.

[8] Xu X P,Needleman A.Numerical Simulations of Fast Crack Growth in Brittle Solids[J].Journal of the Mechanics & Physics of Solids,1994,42(42):1397-1434.

[9] Kopera M A,Cantwell C,Kerr R M,et al.Direct Numerical Simulation of Turbulent Flow over A Backward-facing Step[C]//Meeting of the APS Division of Fluid Dynamics.2011,330(1):349-374.

[责任编辑、校对：李琳]Analysis of Fluid Flow around a Cube Based on Aerodynamic N-S Equations

LIULu

(School of Aircraft,Xi'an Aeronautical University,Xi'an 710077,China)

Flow around is a typical aerodynamic issue,and the generation and formation of vortexes is usually understood with difficulty.This paper aims to study the fluid flow around a cube to demonstrate the generation and evolution of a vortex.Based on the Poisson pressure equation,a discretized Poisson equation was proposed by discrete N-S equation using the collocated mesh projection method,and the results were obtained through SOR.The modeling of this flow was conducted with MATLAB numerical calculation and image processing.The characteristics of fluid flow around a square were analyzed according to the images generated.The results show that the fluid was separated from the tip of the cube,curled up afterward,and generated a reverse vortex,which was immediately decomposed into several discrete vortexes thereafter.Analyzing through such numerical model illustrates the detailed changing process of vortex.

Navier-Stokes equations;flow around cube;numerical simulation

2016-09-01

刘璐(1992-)，女，陕西延安人，博士，主要从事空气动力学以及计算流体力学研究。

O357.5

A

1008-9233(2016)05-0026-03