粗糙集理论在外聘教师教学质量评价中的应用

韩慧蓉

(西安航空学院 理学院，陕西 西安 710077)



粗糙集理论在外聘教师教学质量评价中的应用

韩慧蓉

(西安航空学院 理学院，陕西 西安 710077)

应用粗糙集理论对外聘教师的教学质量进行评价。利用粗糙集理论中的属性简约和重要度计算对评价指标进行约简，得到指标的客观权重，并与主观权重相结合，给出了教师评价的排序结果。

粗糙集理论；教学质量评价；属性约简；客观权重

0　引言

指标权重是决策分析中的重要数值，是评价和决策中的重要依据，确定权重的方法有很多，粗糙集理论[1-3]就是其中的一种。粗糙集理论[4]是由波兰华沙理工大学教授帕拉克(Z.Pawlak)在1982年研究不完整数据和不精确知识的表达运用中提出的。它建立在某种分类机制基础上，把研究对象进行等价划分，在保持分类基础不变的情况下，对属性进行约简，去掉冗余的属性，并可以计算出单个属性的重要度，从而确定各属性的客观权重。

1　粗糙集理论[1]

1.1不可辨识关系

对信息系统IS=(U,A,V,f)，则∀B⊆A，不可辨识关系

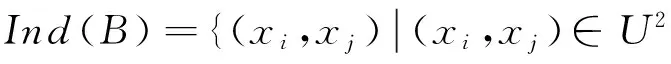
1.2下近似集与上近似集[1]

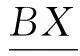
1.3正域、负域、边界

1.4冗余和独立

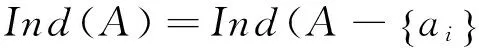
1.5约简和核[5]

约简是与信息系统的属性全集具有相同基本集的最小属性子集。令信息系统IS=(U,A,V,f)，设B⊆A，如果B是独立的，且Ind(B)=Ind(A)，则B是A的一个约简。属性的核是信息系统的属性集合A的所有必要属性构成的集合，记作core(A)。记red(A)为A的所有约简集合，那么存在关系core(A)=∩red(A)。

约简与核是粗糙集理论的两个基本概念。约简是一个信息系统的本质部分，与原系统有相同的辨识性，能识别出所有原信息系统可识别的对象。核是所有约简的共同部分。核和约简可以通过可辨识矩阵来计算。

1.6可辨识矩阵和可辨识函数

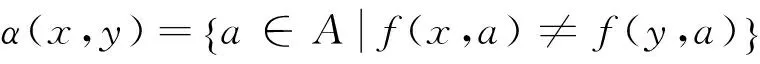
1.7指标的客观权重

2　粗糙集理论客观权重分析流程[6-10]

利用粗糙集理论综合分析客观权重，首先应建立一个信息系统，然后离散化数据指标，再进行信息系统的属性约简，最后确定指标的客观权重。

3　基于顾客满意度的指标权重

3.1建立信息系统

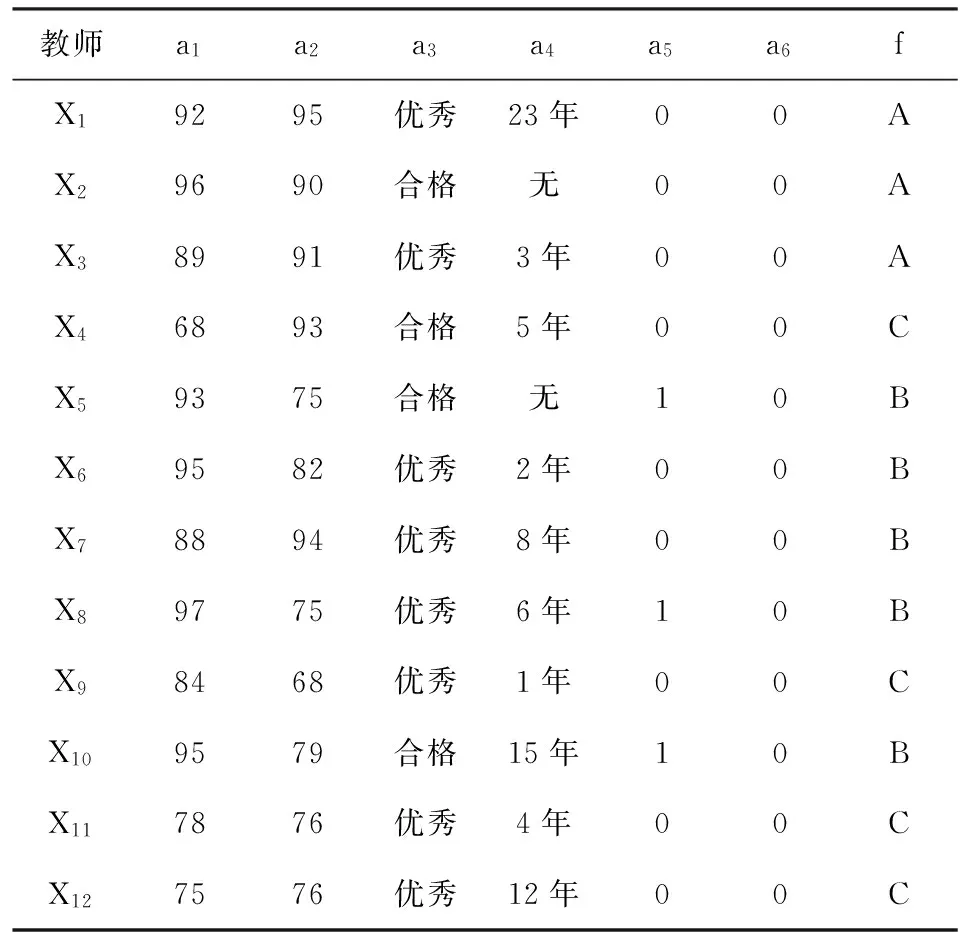
表1　某学校外聘教师各项指标数据信息表

3.2离散化数据

a1，a2：90-100记为1，80-89记为2，70-79记为3，60-69记为4，不及格记为5；a3：优秀记为1，合格记为2；a4：5年以上记为1，1-4年记为2，无教学经验记为3；a5，a6:“有”记为1，“无”记为0。评价结果f：A记为1，B记为2，C记为3。数据经过离散化处理后，得到表2，即为一个信息系统。

表2　某学校外聘教师各项指标离散化数据信息表

3.3信息系统属性约简

为了进行信息系统的属性约简，根据表2建立区分矩阵表3。其中每个对象自己和自己不区分。区分矩阵是一个12×12的矩阵，由于篇幅所限，表3只列出其中部分数据。

表3　顾客满意体验区分矩阵表

可识别函数

f(A)=(a3∨a4)(a1∨a4)(a1∨a3)…

(a2∨a3∨a5)(a1∨a2∨a4)(a1+a2)…

(a1∨a2)(a1∨a2∨a4)…a4

=a1a2a3a4

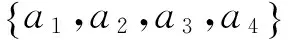
3.4各指标的权重[10]

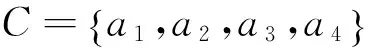
表4　指标约简外聘教师评价信息表

论域U对于决策属性D的划分是：

POSC(D)=U

由公式

=0.333，即a1的重要度是0.333；

同理可得

σCf(a2)=0.5

σCf(a3)=0

σCf(a5)=0.167

归一化后，得到评价指标中学生评分、学校检查评分、教学规范程度、教龄的客观权重分别是0.333,0.5,0,0.167，按照经验，学生评分、学校检查评分、教学规范程度(优秀按照90分计，合格按照80分计)、教龄，有无调停课、有无教学事故分别的主观权重分别是0.3,0.2,0.1,0，并按照主观权重和客观权重分别占30%，70%，对每位外聘教师赋分值，得到12位外聘教师x1,x2,x3,x4,x5,x6,x7,x8,x9,x10,x11,x12的分值分别74.0639,70.3176,69.1166,63.0853,63.1983,67.2483,70.608,65.4921,57.8373,67.238,59.5294,59.4953，排序结果是x1,x7,x2,x3,x6,x10,x8,x5,x4,x11,x12,x9。

4　结论

通过以上分析，原有的教师评价结果更依赖于主观判断，在教师人数较多时评价结果不够准确，也可能会出现偏差，例如教师X7，原评价结果是B，而计算排序结果是第二名。利用粗糙集给出评价指标的客观权重，并与主观权重相结合，既有效避免了主观偏差，又克服了客观权重在信息不明确的情况下出现的数据失真，所以更准确、更具有说服力。

[1] 张文修.粗糙集理论与方法[M].北京：科学出版社，2001:2-13.

[2] 苗夺谦，李道国.粗糙集理论、算法和应用[M].北京：清华大学出版社，2008:82-122.

[3] 王彪，段禅伦，吴昊，等.粗糙集与模糊集的研究及应用[M].北京：电子工业出版社，2008:2-30.

[4] Pawlak Z.Rough Set[J]Internationgnal Journal of Computer and Information Science,1982(11):341-356.

[5] 张文修.粗糙集属性简约的一般理论[J].中国科学(E辑 信息科学)，2005，35(12):1304-1313.

[6] 卢鹏，吴健乐.粗糙集层次分析法在学生综合评价中的应用[J].宜宾学院学报，2015，15(6):103-107.

[7] 韦良.粗糙集理及其应用于发展研究[J].电脑知识与技术，2008，4(1):172-174.

[8] 韩祯祥，张琦，文福拴.粗糙集理论及其应用综述[J]，控制理论与应用，1999，16(2)：153-155.

[9] 李永敏，朱善军，等.基于粗糙集理论的数据挖掘模型[J]，清华大学学报(自然科学版)，1999，39(1)，110-113.

[10] 孙斌，王立杰.基于粗糙集理论的权重确定方法研究[J]，计算机工程与应用，2006(29)：216-217.

[责任编辑、校对：周千]

Application of Rough Set Theory to the Teaching Quality Evaluation of Part-time Teachers

HANHui-rong

(Faculty of Science,Xi'an Aeronautical University,Xi'an 710077,China)

The rough set theory is applied to the teaching quality evaluation of part-time teachers.Attribute reduction and importance calculation in the theory are employed to reduce evaluation indexes.Their objective weights are obtained,and combined with subjective weights to produce the sorting result of part-time teachers.

rough set;teaching quality evaluation;attribute reduction;objective weight

2016-07-04

韩慧蓉(1971-)，女，山西盂县人，副教授，从事基础数学方面的研究。

O221.6

A

1008-9233(2016)05-0065-04