NOD随机变量阵列的q阶矩完全收敛性的充分条件

王 韦 霞

(安徽机电职业技术学院 基础教学部，安徽 芜湖 241003)



NOD随机变量阵列的q阶矩完全收敛性的充分条件

王 韦 霞

(安徽机电职业技术学院 基础教学部，安徽 芜湖 241003)

利用Rosenthal不等式及截尾法，给出了1≤q≤2和q>2两种情形下NOD(negativelyorthantdependent)随机变量阵列q阶矩完全收敛性的充分条件，推广了已有的结论。

NOD随机变量；q阶矩；完全收敛； 截尾法

Joag-Dev等[1- 2]引入了NOD(negatively orthant dependent)序列概念，并指出NOD是严格弱于NA(negatively association dependent)的，而NA在许多领域都有广泛的应用。由于完全收敛蕴含几乎处处收敛，矩完全收敛又蕴含完全收敛，因而研究NOD矩完全收敛受到统计研究者的重视。目前，关于完全收敛已有不少成果， Wu[3]讨论NOD阵列加权和完全收敛性的充要条件，Guo等[4]给出了NA阵列矩完全收敛性的充分条件，Liang等[5]建立了独立同分布NA阵列的q阶矩完全收敛性的充要条件。本文将文献[4-5]的结论推广到NOD阵列，建立了1≤q≤2和q>2两种情形下NOD阵列q阶矩完全收敛性的充分条件。

在给出本文结论之前，先介绍相关的定义及引理，其中，这些引理建立了NOD随机变量阵列的Rosenthal不等式。

定义1称随机变量X1,X2,…,Xn是NUOD(negativelyupperorthantdependent)的，如果对任意的实数x1,x2,…,xn，有

定义2称随机变量X1,X2,…,Xn是NLOD(negativelylowerorthantdependent)的，如果对任意的实数x1,x2,…,xn，有

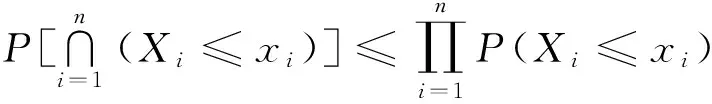
若随机变量{X1,X2,…,Xn}既是NUOD，又是NLOD的，则称该随机变量是NOD。

引理1设{X1,X2,…,Xn}是NOD随机变量阵列，EXi=0，E|Xi|s<∞(1≤i≤n,1≤s≤2)，则存在仅依赖于s的正常数C(与n无关)，有

引理2设{X1,X2,…,Xn}是NOD随机变量阵列，EXi=0，E|Xi|s<∞(1≤i≤n,s>2)，则存在仅依赖于s的正常数C(与n无关)，有

引理3设X是随机变量，β>0，γ>0，s≥0，则下列3个条件等价：

(i)E|X|γ+(α+1)/βlogs|X|<∞；

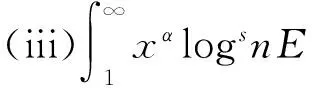
引理4设X是随机变量α<-1，β>0，γ>0，则下列3个条件等价：

(i)E|X|γ+(α+1)/βlogs|X|<∞；

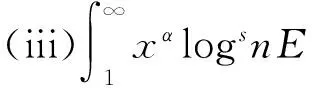
下面给出本文的主要结论及其证明。

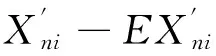
(2)E|X″ni-EX″ni|r≤CE|Xni|rI(|Xni|>1)

(3)

由条件(i)，(ii)可知定理1得证。

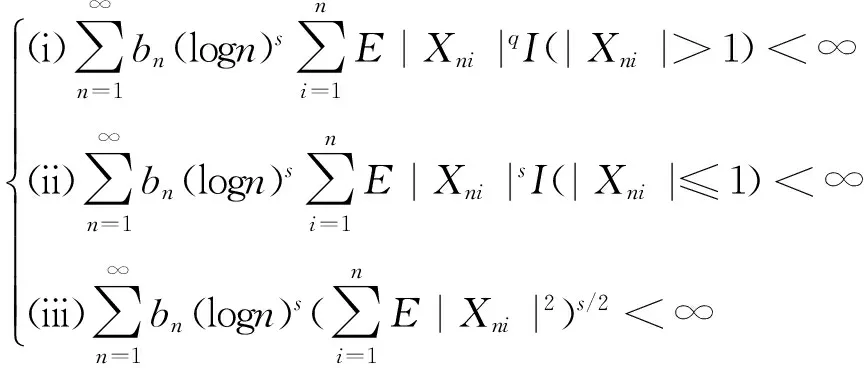
本次物探测区岩矿电性参数通过标本测定获取，标本主要采集于钻孔岩心、露头及坑道，共采集标本307块。利用加拿大产GDD-SCIP型电性参数仪测试，采用恒压模式，测试时记录标本长度，标本截面积等数据，将其输入仪器，测量视电阻率、视极化率参数。测试结果见表1。

证明运用定理1的截尾法和(1)-(3)式及引理2，有

结合已知条件，定理得证。

定理3设{X,Xn,n≥1}是同分布的行为NOD阵列，且EX=0，r≥1，p>1/2，q≥1，r/p≥1，若

(4)

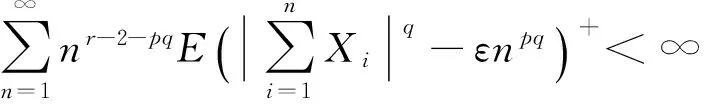
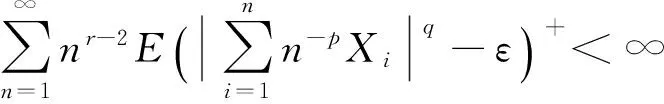
要证明结论成立，只要证明I1<∞，I2<∞，I3<∞。首先证I1<∞成立。

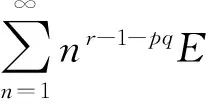
下面证明I2<∞成立，分2种情形讨论[8-10]。

情形1当max{q,r/p}≤2时，由(4)式蕴含E|X|r/p<∞，注意到r-1-2p<-1，由引理4及s>2，有

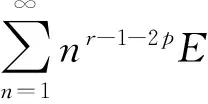
E|X|r/q<∞；

最后证明I3成立，由(4)式蕴含EX2<∞，取充分大的s>r/p，使得r-2+(1-2p)s/2<-1，从而有

[1] Joag-Dev K, Proschan F. Negative association of random variables with applications[J]. Annals of Statistics, 1983, 11(1): 286-295.

[2] Hsu P L, Robbins H. Complete convergence and the law of large numbers[J]. Proceedings of the National Academy of Sciences of the United States of America, 1947, 33(2): 25-31.

[3] Wu Q Y. Complete convergence for weighted sums of sequences of negatively dependent random variables[J]. Journal of Probability and Statistics, 2011, DOI：10.1155/2011/202015.

[4] Guo M L, Zhu D J. On complete moment convergence of weighted sums for arrays of rowwise negatively associated random variables[J]. Journal of Probability and Statistics, 2012, DOI:10.1155/2012/850608.

[5] Liang H Y, Li D L. Rosalsky A.Complete moment and integral convergence for sums of negatively associated random variables[J]. Acta Mathematica Sinica(English Series), 2010,26(3): 419-432.

[6] 郭明乐，张杨杨，祝东进. NOD随机变量序列加权和的矩完全收敛性[J]. 高校应用数学学报(A辑), 2013, 28(1):34-42.

[7] 邱德华. NOD随机变量阵列加权乘积和的完全收敛性[J]. 高校应用数学学报(A辑), 2011,26(1): 34-42.

[8] 管梅. NOD序列加权和的完全收敛性[J]. 佳木斯大学学报, 2014, 32(2): 318-320.

[9] 谭闯, 郭明乐, 祝东进, 等. 行为 ND 随机变量阵列加权和的矩完全收敛性[J]. 山东大学学报(理学版), 2015(6): 27-32.

[10] 夏凤熙, 邓新, 郑璐璐, 等. 矩条件下NA随机变量的强极限定理[J]. 中国科学技术大学学报, 2015, 45(6): 460-464.

Sufficient Conditions for Complete qthMoment Convergence of NOD Random Variables

WANG wei-xia

(Department of Basic Course,Anhui Technical College of Mechanical and Electrical Engineering, Wuhu, Anhui 241003, China)

By using Rosenthal inequality and truncated method, we establish the sufficient conditions of complete qthmoment convergence of negatively orthant random variables by two kinds of cases： 1≤q≤2 and q>2.The conclusions enrich the known results.

arrays of NOD; qthmoment; complete moment convergence; truncated method sufficient conditions

2016-01-08

安徽省教育厅自然科学基金(KJ2015A418，KJ2015A441)。

王韦霞，女，广西崇左人，硕士，安徽机电职业技术学院基础教学部讲师，研究方向为随机极限理论。E-mail: ahjdwwx@126.com

时间：2016-8-17 11:31

http://www.cnki.net/kcms/detail/34.1150.N.20160817.1131.008.html

O211.4

A

1007-4260(2016)03-0025-03

10.13757/j.cnki.cn34-1150/n.2016.03.008