Adams谱序列的一些注记

杜　瑞，王玉玉

（天津师范大学数学科学学院，天津300387）

Adams谱序列的一些注记

杜瑞，王玉玉

（天津师范大学数学科学学院，天津300387）

利用May谱序列证明了，当n＞3时，乘积元素是非平凡的，并且和h0gn在Adams谱序列中不是dr（r≥2）边缘，其中：p≥5，q=2（p-1）.

May谱序列；Ext群；Adams谱序列；dr微分；非平凡性

设p≥5为任意奇素数，A为模p的Steenrod代数，S为球谱.研究球面稳定同伦群的一个重要也很有效的工具是Adams谱序列［1］：其中是A的上同调.如果中的一族生成元xi在Adams谱序列中是永久循环且非平凡地收敛到π*S中的一个同伦元素fi，则fi在Adams谱序列中有滤子s，并由表示.证明一个元素在Adams谱序列中永久循环且收敛到π*S中的一个非零元，一般需要做3项工作∶①证明该元素非平凡；②证明其不是dr（r≥2）边缘；③研究由Adams谱序列向π*S扩张的问题.文献［2］在证明乘积元素的收敛性时，即做了以上3项工作.然而，到目前为止，对包含第四希腊字母类元素的乘积元素进行考查时，后2方面问题并没有结论.如文献［3］仅证明了乘积元素的非平凡性.本研究考查乘积元素对其做前2项工作，为进一步发掘球面稳定同伦群的新元素做准备，而做这2项工作的有力工具是May谱序列.

1　Ext群和May谱序列的一些预备知识

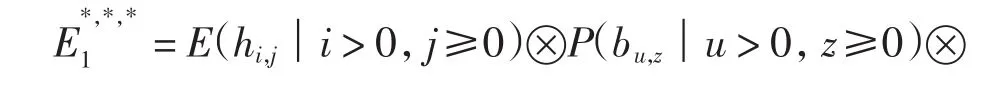
引理令t=q（cnpn+cn-1pn-1+…+c1p+c0）+e为正整数，0≤ci＜p（0≤i＜n），0＜cn＜p，0≤e＜q.设s为任意正整数，0＜s＜p，如果e＞s，那么在May谱序列中有

2　主要结果

定理1当p≥5，n＞3时，有

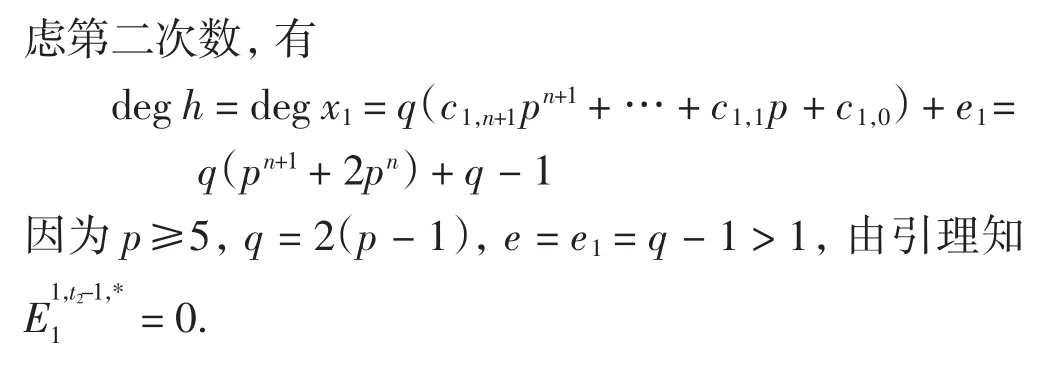
注由本节定理，可以进一步考虑本研究所考查的2个元素与希腊字母类元素α（n）s（n=1，2，3，4）复合后的乘积元素的收敛性，从而发掘出更多的球面稳定同伦群中的非平凡元素.

［1］ADAMS J F.Stable Homotopy and Generalised Homology［M］.Chicago∶Univeristy of Chicago Press，1974.

［2］LIU X G.A nontrivial product of filtration s+5 in the stable homotopy of spheres［J］.Acta Mathematica Sinica，2007，23（3）：385-392.

［3］ZHONG L N，LIU X G.Non-triviality of the productin the Adams spectral sequence［J］.Acta Mathematica Scientia，2014，34（2）∶274-282.

［4］LIULEVICIUS A.The factorizations of cyclic reduced powers by secondary cohomology operations［J］.Mem Amer Math Soc，1962，42：1-112.

［5］AIKAWA T.3-dimensional cohomology of the mod p Steenrod algebra［J］.Mathematica Scandinavica，1980，47：91-115.

［6］RAVENEL D C.Complex Cobordism and Stable Homotopy Groups of Spheres［M］.Orlando∶Academic Press，1986.

（责任编校马新光）

Some notes on Adams spectral sequence

DU Rui，WANG Yuyu
（College of Mathematical Science，Tianjin Normal University，Tianjin 300387，China）

By using the May spectral sequence，it is proved that the two productsare nontrivial，and both of them are not the dr-boundary in the Adams spectral sequence，where n＞3，p≥5，q=2（p-1）.

May spectral sequence；Ext group；Adams spectral sequence；dr-differential；nontriviality

O189.23

A

1671-1114（2016）02-0006-04

2015-07-16

国家自然科学基金资助项目（11301386）；天津市青年骨干教师资助计划项目（ZX110QN044）；天津师范大学博士基金资助项目（52XB1011）.

杜瑞（1991—），女，硕士研究生.

王玉玉（1979—），女，教授，主要从事球面稳定同伦群方面的研究.