基于最小推理机的模糊系统一阶逼近性

索春凤，王贵君

（天津师范大学数学科学学院，天津 300387）

基于最小推理机的模糊系统一阶逼近性

索春凤，王贵君

（天津师范大学数学科学学院，天津 300387）

推理机在模糊系统的前件模糊集运算中起着关键性作用.通过引入最小推理机（最小算子），重新建立一种模糊系统，利用多元函数微分中值定理和最小运算的性质证明了该模糊系统对连续可微函数具有一阶逼近性.

最小推理机；模糊系统；微分中值定理；最大模；一阶逼近性

自日本学者Takagi-Sugeno［1］首次提出T-S模糊系统以来，人们对该模糊系统的研究兴趣与日俱增.文献［2-3］利用基函数和分层思想讨论了模糊系统的泛逼近性，得到了一些有益的结果.文献［4］提出了分片线性函数的概念，并以此为桥梁讨论了广义T-S模糊系统对P-可积函数的逼近性.文献［5］借助分片线性函数研究了广义Mamdani模糊系统在K-积分模下的逼近性.然而，文献［4-5］虽然借助分片线性函数从理论上证明了一些模糊系统的逼近性能，但并没有给出分片线性函数的具体解析式.文献［6］利用超平面思想构造了一个分片线性函数的具体解析表达式，从而为继续探究模糊系统的逼近性提供了一个方便工具.本研究基于最小推理机（最小算子）、单点模糊化和中心平均解模糊化构造了一般模糊系统模型，并利用多元函数微分中值定理证明了该系统对连续可微函数具有一阶逼近性.

1　系统的构造

本节首先给出一致完备标准前件模糊集的定义；其次，基于最小推理机、单点模糊化和中心平均解模糊化重新构造一种模糊系统.

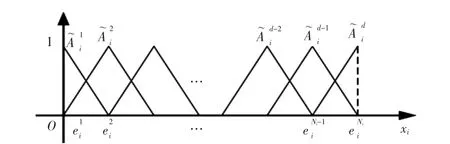
图1　xi轴上一组一致完备标准的模糊集Fig.1　A set of uniform complete fuzzy sets on xiaxis

事实上，该模糊系统共有M=N1×N2×…×Nd条IF-THEN模糊规则，每条规则形式为

其中：i1=1，2，…，N1；i2=1，2，…，N2；…；id=1，2，…，Nd；而为第i1i2…id条规则输出模糊集，不妨用表示模糊集的中心.

下面，根据式（1）中N1×N2×…×Nd条规则，采用最小推理机、单点模糊化和中心平均解模糊化构造一般模糊系统f（x）如下：

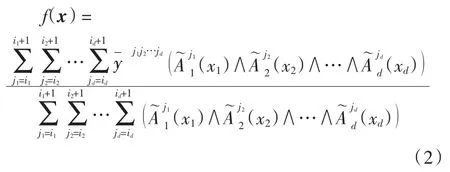
其中x=（x1，x2，…，xd）∈U⊆Rd，且按定义的完备性知式（2）分母部分恒不为0.

2　系统的逼近性

下面针对式（2）所确定的数学模型，利用多元微分中值定理证明一般模糊系统f（x）在最大模意义下对连续可微函数具有一阶逼近性.

引理设多元函数f（x1，x2，…，xd）在凸区域D⊂Rd内的点上均可微，则对区域D内任意2点P（a1，a2，…，ad）、Q（a1+h1，a2+h2，…，ad+hd），必存在θ∈（0，1），使得

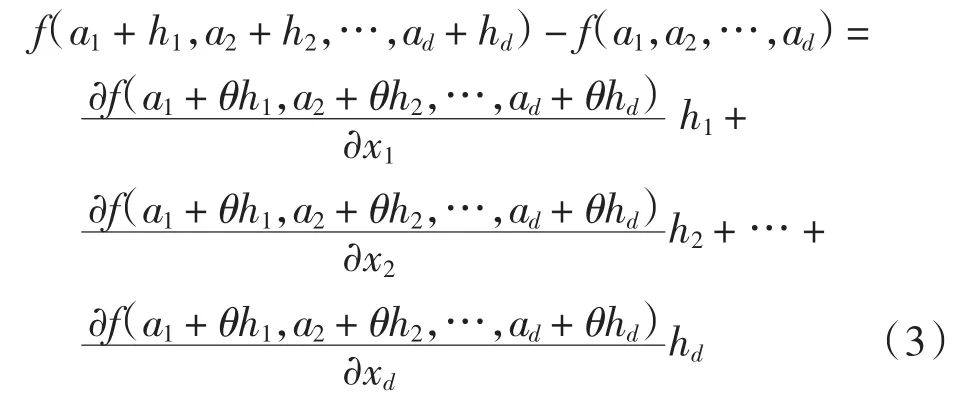
［1］TAKAGI T，SUGENO M.Fuzzy identification of system and its applications to modeling and control［J］.IEEE Transactions on Systems，Man，Cybern，1985，15（1）：116-132.

［2］WANG L X，MENDEL J.Fuzzy basis functions，universal approximation，and orthogonal least-squares learning［J］.IEEE Transanctions Neural Networks，1992，3（5）：807-814.

［3］WANG L X.Universal approximation by hierarchical fuzzy systems［J］.Fuzzy Set and Systems，1998，93（1）：223-230.

［4］刘普寅，李洪兴.广义模糊系统对于可积函数的逼近性［J］.中国科学：E辑，2000，30（5）：413-423.LIU P Y，LI H X.Approximation of a generalized fuzzy system to integrable functions［J］.Science in China：Series E，2000，30（5）：413-423（in Chinese）.

［5］王贵君，李晓萍，隋晓琳.广义Mamdani模糊系统依K-积分模的泛逼近性及其实现过程［J］.自动化学报，2014，40（1）：143-148.WANG G J，LI X P，SUI X L.Universal approximation and its realization of generalized Mamdani fuzzy system based on K-integral norms［J］.Acta Automatica Sinica，2014，40（1）：143-148（in Chinese）.

［6］彭维玲.基于剖分模糊系统输入空间的多维分片线性函数的构造及逼近［J］.系统科学与数学，2014，34（3）：340-351.PENG W L.Structure and approximation of a multi-dimensional piecewise linear function based on the input space of subdivision fuzzy systems［J］.Journal of Systems Science and Mathematical Sciences，2014，34（3）：340-351（in Chinese）.

［7］王立新.模糊系统与模糊控制教程［M］.北京：清华大学出版社，2003.WANG L X.Courses of Fuzzy System and Fuzzy Control［M］.Beijing：Tsinghua University Press，2003（in Chinese）.

（责任编校马新光）

First-order approximation of fuzzy system based on minimum inference engine

SUO Chunfeng，WANG Guijun
（College of Mathematical Science，Tianjin Normal University，Tianjin 300387，China）

Inference engine plays a key role in the antecedent fuzzy sets of fuzzy system.A new fuzzy system is established by introducing minimum inference engine（minimum operator），and through the differential mean value theorem for multivariate function and some properties of the minimum operation，the first-order approximation of the fuzzy system to a continuous differentiable function is proved

minimum inference engine；fuzzy system；differential mean value theorem；maximum norm；the first-order approximation

O159；TP183

A

1671-1114（2016）02-0010-03

2015-06-20

国家自然科学基金资助项目（61374009）.

索春凤（1990—），女，硕士研究生.

王贵君（1962—），男，教授，主要从事模糊神经网络、模糊系统、模糊测度与积分方面的研究.