一种刚性杆-弹簧摆模型的混沌动力学行为研究

赵　聪，于洪洁

(上海交通大学工程力学系，上海 200240)



一种刚性杆-弹簧摆模型的混沌动力学行为研究

赵聪，于洪洁

(上海交通大学工程力学系，上海 200240)

针对具有大范围运动慢变量和小幅度振荡快变量的强非线性刚-柔耦合多体系统，建立一种刚性杆-弹簧摆模型。给出了该双时间尺度变量系统的无量纲动力学方程，以频率比、摆长比作为控制参数，对系统在不同初始条件下的非线性动力学行为进行了数值模拟和分析。由于快、慢变量之间的相互耦合，动力学方程表现出强非线性的特点，对数值方法提出了更高要求。采用一种高精度的三次Lagrange插值精细积分法进行数值求解，并给出了系统不同的运动状态对应的参数范围。数值分析结果表明，系统变量在不同的控制参数和初始条件下，呈现出了复杂的混沌动力学行为，快变量显示了经由准周期环面破裂分岔通往混沌的途径。

刚-柔耦合系统；双时间尺度；弹簧摆；插值精细积分法；混沌

刚-柔耦合多体系统是目前常见的力学模型，在工程中有着非常广泛的应用，例如直升机旋翼、柔性机械臂、涡轮机叶片等等。该类系统的大范围刚体运动与弹性小变形运动的耦合使得系统的动力学性态十分复杂，其动力学方程具有强非线性，随之带来的动力刚化现象、数值求解的困难等是建立该类模型时需要重点考虑和解决的问题。

平面双摆刚体系统是混沌动力学中的经典模型，Stachowiak T等[1]和Nikitina N V[2]对平面双摆系统的混沌运动等动力学行为作了相关研究。弹簧摆系统也是比较典型的非线性运动模型之一，在不考虑弹簧的扭振和扭转变形，只考虑弹簧纵向伸长时，弹簧摆是一个简单的二自由度系统。近年来，国内外学者对弹簧摆作了许多方面的研究，例如弹簧摆的内共振现象[3-5]、混沌运动[6-7]等。文献[8]研究了弹簧摆系统在频率比以及初值条件变化时的混沌、拟周期运动等复杂动力学行为。对于将平面双摆刚体系统与弹簧摆系统结合起来构成的更复杂的刚性杆—弹簧摆系统的研究目前还鲜有发表。

钟万勰[9-10]针对线性定常结构动力系统提出了一种精细时程积分法，这种方法具有高精确度、高效、稳定的特点，它的解在积分点处数值上逼近于精确解。张洵安[11]等指出非线性精细积分算法可有效地计算多自由度系统的混沌运动。精细积分法经众学者的改进，已经得到了长足发展和广泛应用，例如更新精细积分方法[12]、增维精细积分法[13-15]，三次Lagrange插值精细积分法[16]等等。其中，本文作者提出的三次Lagrange插值精细积分法[16]是一种单步显式、预估-校正的具有四阶精度的算法，具有自起步、精度高及计算量小的特点，适用于求解强非线性动力学方程。

本文结合了平面双摆系统和弹簧摆系统的特点，构造了更为复杂的刚性杆-弹簧摆模型，该模型是三自由度双时间尺度变量系统。其中，两个慢变量分别为刚性杆和弹簧的摆角，对应刚-柔耦合系统的大范围运动；快变量为弹簧伸长率，对应刚-柔耦合系统的弹性小变形。以参数频率比描述快、慢变量之间的时间尺度差异。由于变量之间的耦合，系统动力学方程具有强非线性的特点，采用本文作者提出的一种三次Lagrange插值精细积分法[16]对无量纲化的动力学方程进行数值求解。结合Poincaré映射和最大Lyapunov指数等数值手段，对系统的非线性动力学行为进行分析。

1　模型的建立及动力学方程推导

如图1所示，建立刚性杆-弹簧摆平面运动模型。质量分布均匀的刚性细杆在x-y平面内绕支点O摆动，弹簧摆与刚性杆的下端铰接。假设弹簧不发生扭转变形和扭振，并且不计质量，小球可视为质点。系统受y方向的重力作用作平面运动，不计一切摩擦力。其中：刚性杆的质量为m1，长度为l1，相对于竖直方向的摆动角度为θ1；弹簧的刚度为k，原长为l0，动态摆长为r，相对于竖直方向的摆角为θ2，小球质量为m2。

设系统静平衡时弹簧的长度为l，由受力分析得到：l=l0+m2g/k。根据第二类Lagrange方程建立系统的动力学方程：

(1)

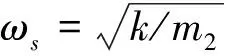
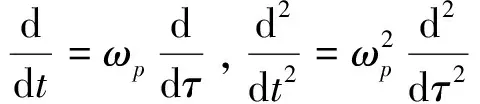
(2)

方程(2)描述了一个三自由度双时间尺度变量刚—柔耦合系统，其中刚性杆的摆角θ1和弹簧摆的摆角θ2是慢变量，弹簧伸长率x是快变量，它们之间相互耦合；该方程为无量纲方程，具有强非线性，含有两个控制参数：频率比γ1、摆长比γ2。

2 三次Lagrange插值精细积分法

动力学系统微分方程的一般形式为

(3)

其中,x是n维向量，n是自由度数；r(t)是时变的载荷向量；α和β是已知的初始条件。

由于精细积分法易于处理一阶方程，因而将式(3)化成下列一阶常微分方程

(4)

其中，v是2n维向量，H是2n×2n阶的满秩常矩阵，f(t)是由r(t)构成的已知列向量。

vk=v(kτ)=exp(Hkτ)v0=exp(Hτ)vk-1=Tvk-1

(5)

其中，矩阵T可由文献[1]给出的方法精确计算出来，进而计算出解向量，得到各离散时刻的解vk。

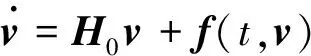
(6)

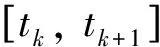
P3(t,v(t))=r0+r1(t-tk)+r2(t-tk)2+r3(t-tk)3

(7)

插值基点取

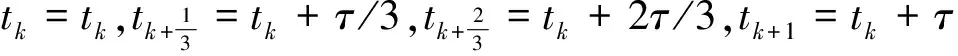
r0=f(tk,v(tk))≡fk

(8)

用Euler公式取vk+1的预测值[16]，将式(8)代入式(7)求出P3(t,v)，将其代入式(6)，令t=tk+1，积分得

(9)

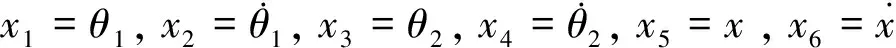
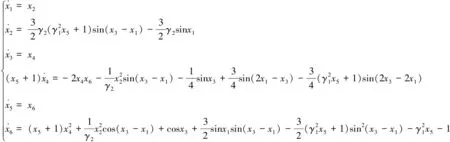
(10)

式(10)是具有强非线性的无量纲一阶微分方程组。由式(4)，构造出非线性函数f(t,v)、H0分别为

3　刚性杆-弹簧摆系统非线性动力学行为分析

本节主要研究刚性杆-弹簧摆系统在不同的初始条件下随着控制参数的变化而表现出的不同动力学行为。刚-柔耦合多体系统具有快、慢变量及多参数的特点。考虑到工程实际，参数频率比γ1的取值不宜过大或过小。根据频率比的定义，γ1值的大小一定程度上反映了系统快、慢变量之间时间尺度相差程度的大小。若频率比值取得过大，系统表现出很强的刚性，难以和多刚体系统区分开来；反之，则表现出很强的柔性。因此，首先设定一组固定参数：频率比参数为定值γ1=50，摆长比参数γ2=1，刚性杆初始摆角θ10=45°，弹簧摆初始时刻为竖直状态，即θ20=0°，弹簧初始伸长率x0=0.001。通过数值计算，观察系统变量的时程曲线、相轨迹图，并结合Poincaré映射和最大Lyapunov指数等数值手段对系统变量的运动状态进行分析。

图2a、b、c分别为系统慢变量刚性杆摆角θ1、弹簧摆摆角θ2和快变量弹簧伸长率x在θ10=45°时的Poincaré映射图。图2a显示刚性杆摆角θ1的Poincaré映射点组成带状的环面；图2b、2c显示弹簧摆摆角θ2和弹簧伸长率x的Poincaré映射点为模糊一片的密集点集，表现出混沌运动的特征；从图中还可看出，弹簧摆摆角θ2的最大值小于0.15 rad (8.6°)，尽管刚性杆的初始摆角达到45°，弹簧摆的摆动仍处于小角度范围内。经计算得出，此时系统最大Lyapunov指数λ1=0.909 014 7，可判定出现混沌运动。

下面考虑刚性杆初始摆角θ10的值在5°～50°大范围内变化，其他参数条件不变。图3a～d分别显示当θ10=5°,20°,40°,50°时，系统快变量弹簧伸长率x的Poincaré映射图。从图中可以看出，当θ10=5°时，快变量x的Poincaré映射点近似于准周期运动对应的一条封闭曲线，随着θ10值的增大，Poincaré映射环面逐渐破裂，最终形成一大片模糊点集。图3a～d四种情况下对应的系统最大Lyapunov指数λ1分别为1.828 782×10-5、2.036 442×10-5、0.087 738 55、0.946 333 2。由此可推测快变量弹簧伸长率x可能经由准周期环面破裂分岔这一途径通往混沌。

随后，设定频率比参数为定值γ1=20，考虑摆长比参数γ2的变化对系统状态变量动力学行为的影响。仍然取弹簧初始伸长率x0=0.001，弹簧摆初始时刻竖直，即θ20=0°，令γ2在0.25～4范围内变化，刚性杆初始摆角θ10在5°～50°大范围内变化，观察参数组合条件下的系统变量Poincaré映射图，并计算相应的系统最大Lyapunov指数。表1给出在部分γ2值下系统最大Lyapunov指数的变化情况，图4是相应的变化曲线。

由表1可以看出，在所研究的参数范围内，计算得到的系统最大Lyapunov指数均为正数。随着刚性杆初始摆角θ10的增大，系统最大Lyapunov指数有增大的趋势。摆长比γ2越小，系统最大Lyapunov指数增大到10-1量级时对应的θ10临界值越小，结合图4，即摆长比γ2越小，系统最大Lyapunov指数随刚性杆初始摆角θ10增长的越快。

4　结论

构建了一种三自由度双时间尺度变量刚—柔耦合系统——刚性杆—弹簧摆模型，体现了刚—柔耦合多体系统中大范围运动慢变量与弹性小变形快变量耦合的特点。对于此类容易产生刚性问题的强非线性动力学方程，采用一种三次Lagrange插值精细积分法进行数值求解，该方法具有单步显式、预估—校正、自起步、四阶精度等特点。将频率比、摆长比以及刚性杆初始摆角作为控制参数，研究了慢变量、快变量不同的动力学行为。发现了慢变量的混沌行为和快变量经由准周期环面破裂通往混沌的途径。工程实际中包含很多类似的刚—柔耦合多体系统，例如柔性机器人手臂等，研究本文模型大范围运动和自身形变在合理参数范围内的耦合非线性动力学行为，对工程中针对此类模型进行设计和控制具有相当的参考价值。

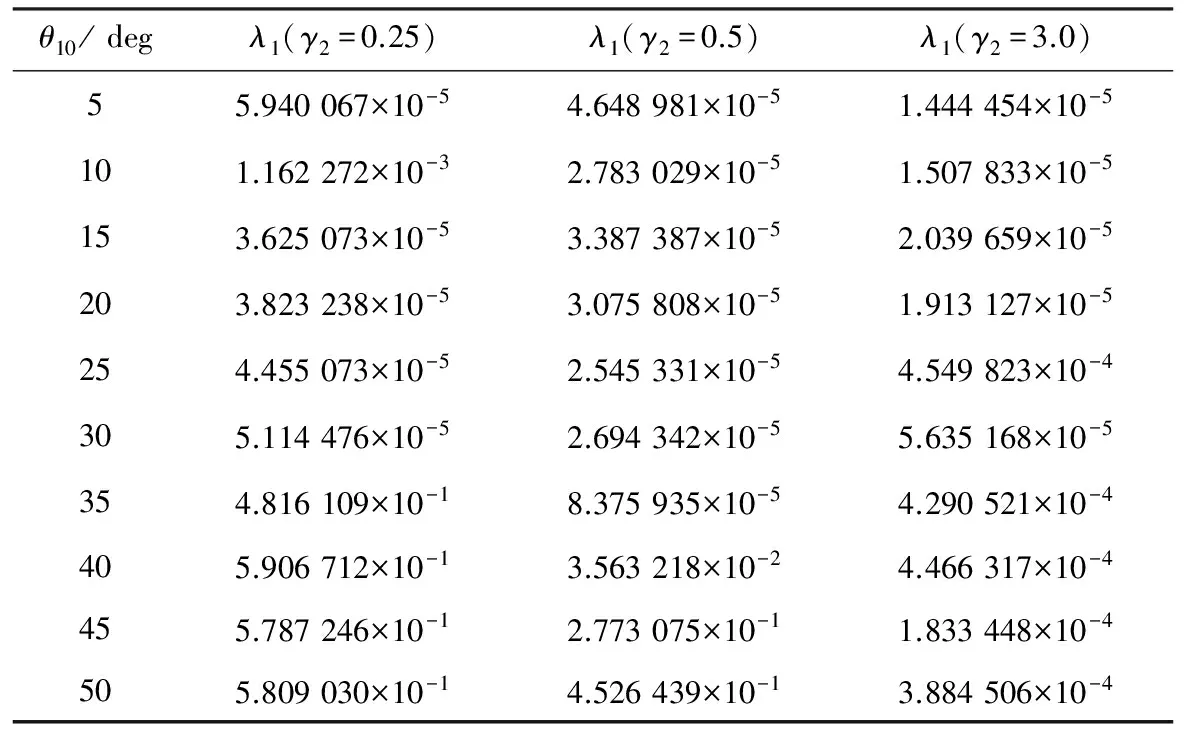
表1　系统最大Lyapunov指数λ1随控制参数变化的情况

[1]Stachowiak T, Okada T. A numerical analysis of chaos in the double pendulum[J]. Chaos, Solitons & Fractals, 2006, 29(2): 417-422.

[2]Nikitina N V. Ultimate energy of a double pendulum undergoing quasiperiodic oscillations[J]. International Applied Mechanics, 2007, 43(9): 1035-1042.

[3]司丽荣, 张竞夫. 弹簧摆内共振现象的实验研究[J]. 物理实验, 2002, 22(3): 9-12.

Si Lirong, Zhang Jingfu. Study on the experiment of the autoparametric resonance of a spring fendulum[J]. Physics Experimentation, 2002, 22(3): 9-12.

[4]Lee W K, Park H D. Chaotic dynamics of a harmonically excited springpendulum system with internal resonance[J]. Nonlinear Dynamics, 1997, 14(3): 211-229.

[5]Zheng J L, Yu X W. Analysis of the autoparametric resonance of a spring pendulum[J]. Physics and Engineering, 2010, 20(2): 13-16.

[6]Van der Weele J P, De Kleine E. The Order-chaos-order sequence in the spring pendulum[J]. Physica A: Statistical Mechanics and its Applications, 1996, 228(1-4): 245-272.

[7]Li Y S, Shu X F. Internal resonance and chaotic motion of a spring pendulum[J]. Journal of Taiyuan University of Technology, 1998, 29(6): 555-559.

[8]于洪洁, 张靖姝, 洪嘉振. 刚柔耦合弹簧摆的复杂动力学行为[J]. 科技导报, 2013, 31(18): 32-38.

Yu Hongjie, Zhang Jingshu, Hong Jiazhen. Complex dynamical behavior of rigid-flexible coupling spring pendulum[J]. Science and Technology Review, 2013, 31(18): 32-38.

[9]钟万勰. 结构动力方程的精细时程积分法[J]. 大连理工大学学报, 1994, 34(2): 131-136.Zhong Wanxie. On precise time-integration method for structural dynamics[J]. Journal of Dalian University of Technology, 1994, 34(2): 131-136.

[10] Zhong W X, Williams F W. A precise time step integration method[J]. Journal of Mechanical Engineering Science, 1994, 208: 427-430.

[11] 张洵安, 杨人风. 结构混沌运动的非线性精细积分计算方法[J]. 西安公路交通大学学报, 2000, 20(2): 99-101.

Zhang Xunan, Yang Renfeng. The method of nonlinear precise integration for chaotic motion of structure[J]. Journal of Xi’an Highway University, 2000, 20(2): 99-101.

[12] Wang M F, Zhou X Y. Renewal frecise time step integration method of structural dynamic analysis[J]. Acta Mechanica Sinica, 2004, 36(2): 191-195.

[13] Gu Y X, Chen B S, Zhang H W. Precise time-integration with dimension expanding method[J]. Acta Mechanica Sinica, 2000, 32(4): 447-456.

[14] Zhang S Y, Deng Z C. Increment-dimensional precise integration method for nonlinear dynamic equation[J]. Chinese Journal of Computational Mechanics, 2003, 20(4): 423-426.

[15] Ge G, Wang H L, Tan G. Improved increment-dimensional precise integration method for the nonlinear dynamic equation with multi-degree-of-freedom[J]. Journal of Tianjin University, 2009, 42(2): 114-117.

[16] 吕和祥, 于洪洁, 裘春航. 精细积分的非线性动力学积分方程及其解法[J]. 固体力学学报, 2001, 22(3): 303-308.

Lv Hexiang, Yu Hongjie, Qiu Chunhang. A integral equation of non-linear dynamics and Its solution method[J]. Acta Mechanica Solida Sinaca, 2001, 22(3): 303-308.

(责任编辑耿金花)

On the Chaotic Dynamic Behaviour of the Rigid Rod-Spring Pendulum Model

ZHAO Cong，YU Hongjie

(Department of Engineering Mechanics, Shanghai Jiaotong University, Shanghai 200240, China)

A planar rigid rod-spring pendulum model was constructed and dimensionless dynamic equation was given. We numerically simulated and analyzed the dynamical behavior of the two-time-scale system while the frequency ratio and length ratio and initial conditions vary. The dynamic equation is strongly nonlinear as the fast and slow variables couple each other. A cubic interpolation precise integration method was applied to solve nonlinear dynamic equation. We also employ the Poincaré maps and the maximum Lyapunov exponent methods. Numerical simulation results demonstrate that the system presents complex chaotic motion in different parameters conditions. It is also found that the fast variable may transform to chaos via the quasi-periodic torus breakdown.

rigid-flexible coupling system; two-time-scale; spring pendulum; interpolation precise integration method; chaos

1672-3813(2016)03-0097-06；DOI:10.13306/j.1672-3813.2016.03.013

2014-09-16；

2015-01-04

国家自然科学基金重点项目(11132007)

赵聪(1990-)，男，辽宁鞍山人，硕士研究生，主要研究方向为非线性动力学。

于洪洁(1968-)，女，辽宁大连人，副教授，博士研究生，主要研究方向为复杂系统非线性动力学，混沌同步与控制。

O313， O322

A