附加失败率检验的长距离参考站网模糊度固定

张　明， 刘　晖， 冯彦同， 周　鹏， 李　伟

(1.武汉大学卫星导航定位技术研究中心，武汉 430079； 2.山东省国土测绘院，济南 250102；3. 广西壮族自治区遥感信息测绘院，南宁 530023)



附加失败率检验的长距离参考站网模糊度固定

张明1， 刘晖1， 冯彦同2， 周鹏1， 李伟3

(1.武汉大学卫星导航定位技术研究中心，武汉 430079； 2.山东省国土测绘院，济南 250102；3. 广西壮族自治区遥感信息测绘院，南宁 530023)

对于长距离参考站网模糊度固定而言，Ratio检验和三角形模糊度闭合差(Triangle Ambiguities Closure Error，TACE)检验是最常用的两种模糊度检验手段，一般认为通过这两种检验后即可将模糊度固定。但事实上，在此情况下，模糊度被错误固定的情况经常出现。为此，本文提出了一种网解失败率(Network Failure Probability，NFP)检验方法，使用该方法可以计算出通过Ratio检验和TACE检验前提下参考站网模糊度固定的失败率。实验表明，当参考站数量小于等于8时，附加NFP检验后模糊度固定的正确率最高提高了25.4%，平均提高了8.1%，初始化成功率平均提高了4.3%。

失败率；长距离；参考站网；模糊度固定；模糊度检验

0　引言

为了避免模糊度被错误固定，得到模糊度整数解后，必须进行模糊度检验。对于长距离参考站网模糊度固定而言，Ratio检验[1]和三角形模糊度闭合差(triangle ambiguities closure error, TACE)检验是最常用的两种模糊度检验手段，Ratio检验属于显著性检验，Ratio值等于模糊度残差二次型次最小值与最小值的比值。Ratio阈值的设置是决定模糊度检验效果的关键，常用的经验阈值有1.5、2.0和3.0[2]。此外，参考站网通常由Delaunay[3]三角形组成，由于任意三角形的双差模糊度闭合差一定为零，因此，TACE检验是一种十分重要的模糊度检验手段。

一般认为通过了Ratio检验和TACE检验后，即可将模糊度固定。但事实上，在此情况下，模糊度被错误固定的情况经常出现。原因有3点：1)是Ratio检验假设模糊度浮点解服从正态分布，但事实上，由于观测模型误差、随机模型误差和其他未模型化误差的影响，导致模糊度浮点解及其方差—协方差阵均是有偏的；2)是常用的Ratio阈值设置方法均为经验值法，缺乏严密的理论基础；3)是TACE为零只是模糊度整数解正确的必要不充分条件。

为此，本文提出了一种NFP检验方法，在参考站网内所有基线均通过Ratio检验和TACE检验的前提下，根据模糊度整数解与真值偏差的分布特性，计算出参考站网模糊度固定的失败率。通过设置合理的失败率阈值，即可提高模糊度固定的正确率。

1　附加失败率检验的参考站网模糊度固定

本文使用非组合观测模型[4]，双差电离层延迟采用参数估计。对流层干延迟采用模型改正，天顶方向湿延迟采用分段常数估计[5]，对流层投影函数使用GMF[6]。此外，本文使用高度角定权策略[7]。

1.1参考站网的失败率

所谓参考站网的失败率，就是参考站网中部分或全部模糊度整数解被错误固定的概率。由于任意非独立基线向量均可由一组独立基线向量表示，在参考站网内所有TACE为零的前提下，如果独立基线全部正确固定，那么非独立基线一定正确，反之部分或全部非独立基线一定错误。因此，可以认为参考站网模糊度固定的失败率等于独立基线组模糊度固定的失败率。由于独立基线间不具有相关性，因此可以分别计算出每条独立基线的成功率和失败率，最终得到的独立基线组的失败率即参考站网的失败率。

1.1.1单基线一维模糊度固定的失败率

(1)

同样，可以得到模糊度错误固定为任意非0整数的概率：

(2)

所有错误情况概率之和，即为模糊度固定的失败率：

(3)

(4)

其中，Ps、Pf分别为模糊度固定的成功率和失败率，上标中第1和第2个数字分别代表基线的维数和模糊度的维数；d为模糊度整数解与真值的偏差；D为模糊度偏差的集合，该集合是非零整数集合的子集。

1.1.2单基线多维模糊度固定的失败率

Dong和Bock[8]，Tuniessen[9]给出了多维模糊度的成功率计算公式，主要思想就是根据bootstrap原理，依次对模糊度取整固定，逐步更新方差—协方差阵，得到各维模糊度的条件方差，然后计算各维模糊度固定的成功率，最后将所有模糊度的成功率相乘，即可得到多维模糊度固定的成功率：

(5)

借鉴该方法，可以计算多维模糊度固定的失败率。首先分别计算第i维模糊度固定的成功率和失败率：

(6)

(7)

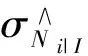
因为每维模糊度固定的状态只有两种：成功或者失败，排除所有模糊度均正确固定的情况，则模糊度固定失败的组合有2n-1种。计算所有失败组合的概率并求和，即可得到单基线多维模糊度固定的失败率。

1.1.3独立基线组模糊度固定的失败率

对于独立基线而言，每条基线固定的状态只有两种：成功或者失败。若参考站数量为m，独立基线的数量为m-1，那么模糊度固定失败的组合有2m-1-1种。分别计算每条独立基线固定的失败率和成功率，计算每种失败组合的概率并求和即可得到独立基线组的失败率，也就是参考站网的失败率。

1.1.4模糊度整数解与真值的偏差

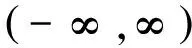
因此，L1模糊度的偏差集合可以表示为

(8)

WL模糊度的偏差集合可以表示为

(9)

1.2参考站网模糊度固定策略

一般不同模糊度的精度不同，要想一次固定所有模糊度需要较长时间。为了加快初始化速度，本文中一次固定所有可能固定的模糊度。由于模糊度整数解必须通过TACE检验，通过该检验的模糊度被正确固定的可能性更高，因此可以优先固定这类模糊度。本文采用的模糊度固定策略如图1所示：

模糊度搜索使用LAMBDA方法[10]，由于WL模糊度波长更长，也更容易固定，因此固定WL模糊度固定以后，再固定对应卫星的L1模糊度。此外，模糊度浮点解小数部分越小，模糊度被正确固定的可能性更高，因此当搜索的模糊度为1维时，本文还使用了模糊度浮点解小数检验法。

2　实验与分析

2.1实验数据与实验方案

为了验证本文提出的方法，共进行了18 720次初始化实验。使用了16个测站共3天的数据，观测时间为2010年的第85、86、87天，采样间隔为30s，截止高度角设为10度。数据来源于SDCORS，测站分布如图2所示。

参考站平均间距为136.6 km，从16个参考站中，随机选择3～15个组成13组参考站网，每组包括10个测站数量相同的参考站网。参考站选取的标准是构成Delaunay三角网后，参考站网中任意基线长度不超过200 km。

在每个整小时处开始初始化，每个参考站网均进行72次初始化解算。分别采用2种方案进行模糊度解算，方案1：使用Ratio检验和TACE检验；方案2，在方案1的基础上增加NFP检验。Ratio阈值设为3.0，Fraction阈值设为0.25周，NFP阈值设为0.001。

如果6颗以上或全部卫星被固定，即认为初始化成功。此外，若某时段不能在240个历元内完成初始化，则认为初始化失败，其结果也不参与模糊度固定正确率的统计。模糊度真值由PANDA[11]软件解算得到，将模糊度整数解与真值进行对比，得到模糊度整数解的偏差及固定的正确率。此外，还分别统计了两种方案的初始化成功率。

2.2模糊度整数解与真值偏差

采用方案1得到的模糊度整数解中，分别有12 063个L1模糊度和7 504个WL模糊度固定错误。说明即使通过了Ratio检验和TACE检验，模糊度被错误固定的情况依然十分严重。模糊度偏差分布情况如图3所示。

从图3可以发现，95%以上的L1模糊度偏差在5周以内，对于WL模糊度而言，偏差为1周的情况占96%以上，验证了本文对模糊度整数解偏差范围的判断。

这也说明错误固定的宽巷模糊度不仅更少，而且与真值的偏差也更小，原因在于宽巷模糊度的波长更长，被正确固定的概率更高，即使被错误固定，其偏离真值的程度也更低。

2.3正确率

模糊度固定正确率的计算公式为

(10)

其中，Rc为模糊度固定的正确率，Ncf为正确固定的模糊度数量，Nf为固定的模糊度总数。

每组参考站网模糊度固定的平均正确率如图4所示。

从图4中可以发现，对于方案1，当参考站数量为3时，模糊度固定的正确率低于73%，这说明仅使用Ratio检验和TACE检验不能保证模糊度固定的正确性。随着参考站网规模的增大，参考站模糊度固定的正确率逐渐上升，当参考站数量达到8时，模糊度固定的正确率接近100%。这是由于随着参考站网规模的增大，基线和三角形的数量逐渐增加，对于同一颗卫星而言，模糊度固定的条件越来越苛刻，因此错误固定的可能性逐渐降低。

当参考站数量为3时，使用NFP检验后模糊度固定的正确率提高了25.4%。随着参考站网规模的增大，由于方案1本身正确率的提高，NFP检验的作用逐步降低，当参考站数量大于8时，方案2相对于方案1没有明显改善。

2.4初始化成功率

初始化成功率的计算公式为

(11)

其中，RS为初始化成功率，Is为成功初始化次数，I为初始化总次数，每组参考站网共初始化720次。

从图5可以看出，参考站网的规模对于初始化成功率没有明显影响，在不使用NFP检验的情况下，初始化成功率均低于95%。未能成功初始化的原因很复杂，其中一个可能的原因是部分被优先固定的模糊度整数解是错误的，其影响相当于在观测值中引入了粗差，导致剩余的模糊度难以固定，这也反映了质量控制的重要性。

灰色曲线反映了方案2初始化成功率相对于方案1的提升，当参考站数量小于等于8时，附加NFP检验后明显提高了初始化成功率，最高提高了6.3%。但随着参考站网规模的增大，NFP检验对于初始化成功率的负面影响越来越严重。原因在于，当参考站数量较少时，使用NFP检验后，提高了模糊度固定的正确率，从而减少了因部分模糊度被错误固定导致无法完成初始化的情况。随着参考站规模的增大，模糊度固定的正确率接近100%，附加NFP检验后，不必要地增加了模糊度固定的难度，因此导致无法在一定时间内完成初始化。

3　结论

Ratio检验和TACE检验不足以保证参考站网模糊度整数解的正确性，为了提高模糊度固定的正确性，本文提出进一步增加NFP检验。在通过Ratio检验和TACE检验的前提下，窄巷模糊度整数解与真值偏差一般不超过5周，宽巷模糊度偏差一般不超过1周。根据该性质，可以计算出参考站网的失败率。

附加NFP检验以后，当参考站数量小于8时，可以明显改善模糊度固定的正确率，当参考站数量为3时提高了25.4%，平均提高了8.1%。由于NFP检验提高了模糊度固定的正确率，因此也将初始化成功率提高了4.3%。当参考站数量大于8时，模糊度固定的正确率接近100%。此时附加NFP检验，无法进一步提高正确率，反而会不必要地增加模糊度固定的难度，因此会降低初始化的成功率。

[1]Euler H J, Schaffrin B. On a measure for the discernibility between different ambiguity solutions in the static-kinematic GPS-mode[C]. International Association of Geodesy Symposia, 1991, 107: 285-295.

[2]Teunissen P J G, Verhagen S. The GNSS ambiguity ratio-test revisited: a better way of using it[J]. Survey Review, 2009, 41(312):138-151.

[3]武晓波，王世新，肖春生. Delaunay三角网的生成算法研究[J].测绘学报，1999，28(1)：28-35.

Wu XiaoBo, Wang ShiXin, Xiao ChunSheng. A new study of Delaunay triangulation creation[J]. Acta Geodaetica et Cartographic Sinica, 1999, 28(1): 28-35.

[4]张明，刘晖，候祥祥，等. 一种用于长距离网络RTK基准站模糊度固定的非组合方法[J]. 测绘科学技术学报，2015，32(1)：32-41.

Zhang Ming, Liu Hui, Hou XiangXiang, et al. Base stations’ ambiguity resolution of long-range network RTK based on uncombined method[J]. Journal of Geomatics Science and Technology, 2015, 32(1): 32-41.

[5]魏子卿，葛茂荣. GPS相对定位的数学模型[M]. 北京：测绘出版社，1998：56-85.

[6]Boehm J, Niell A, Tregoning P, et al. Global mapping function (GMF): a new empirical mapping function based on data from numerical weather model data[J]. Geophysical Research Letters, 2006, 33:L07304.

[7]Ge M, Gendt G, Rothacher M, et al. Resolution of GPS carrier-phase ambiguities in precise point positioning (PPP) with daily observations[J]. Journal of Geodesy, 2008, 82:389-399.

[8]Dong D, Bock Y. Global positioning system network analysis with phase ambiguity resolution applied to crustal deformation studies in California[J]. Journal of Geophysical Research, 1989, 94(B4):3949-3966.

[9]Teunissen P J G. Success probability of integer GPS ambiguity rounding and bootstrapping[J]. Journal of Geodesy, 1998, 72(10):606-612.

[10] Teunissen P J G. The least-squares ambiguity decorrelation adjustment: a method for fast GPS integer ambiguity estimation[J]. Journal of Geodesy, 1995, 70(1):65-82.

[11] Liu J N, Ge M R. PANDA Software and its preliminary result of positioning and orbit determination[J]. Wuhan University Journal of Natural Sciences, 2003, 8(2):603-609.

(责任编辑耿金花)

esolution for Long-Range

tation Network with Additional Failure Probability Test

ZHANG Ming1, LIU Hui1, FENG Yantong2, ZHOU Peng1， LI Wei3

(1. GNSS Research Center, Wuhan University, Wuhan 430079, China；2. Shandong Provincial Institute of Land Surveying and Mapping, Jinan 250102, China；3. Guangxi Zhuang Autonomous Region Remote Sensing Surveying and Mapping Institute, Nanning 530023, China)

Ratio and triangle ambiguities closure error (TACE) tests are two primary validation methods used in ambiguity resolution for long-range reference station network. once they are passed, it is considered the ambiguities could be fixed to integers with a high confidence. However, it is usually found that the ambiguities were wrongly fixed even both the two tests above are passed. To improve the correct rate of ambiguity solutions, we proposed a network failure probability (NFP) test, the failure probability of the reference station network is calculated under the conditions of that the Ratio test and TACE test have been passed. The experiment result shows that, with additional NFP test, the average correct rate of integer ambiguity solutions is raised up by 8.1% with a peak at 23.5%, the average initialization speed is increased by 5.6% as well when the number of the reference stations is smaller than 8.

failure probability; long-range; reference station network; ambiguity resolution; ambiguity test

1672-3813(2016)03-0103-05；DOI:10.13306/j.1672-3813.2016.03.014

2014-05-20；

2015-05-20

国科发高资助项目([2012]38)；国家高技术研究发展计划(863计划)资助项目(2012AA12A209)；国家高技术研究发展计划(863计划)资助项目(2007AA12Z309)

张明(1989-)，男，湖北仙桃人，博士研究生，主要研究方向为长距离网络RTK理论与方法。

刘晖(1968-)，男，北京人，教授，博士，主要研究方向为连续运行参考站(CORS)理论与技术、高精度实时定位、复杂网络和服务科学。

N94

A