异质阈值决策规则下的复杂网络扩散

肖　宇，韩景倜

(1.上海对外经贸大学商务信息学院，上海 201620；2.上海财经大学 a.信息管理与工程学院，b.实验中心，上海 200433)



异质阈值决策规则下的复杂网络扩散

肖宇1，韩景倜2

(1.上海对外经贸大学商务信息学院，上海 201620；2.上海财经大学 a.信息管理与工程学院，b.实验中心，上海 200433)

基于异质阈值模型和平均场理论刻画了社会网络扩散，分析了邻居效应、阈值分布和网络度分布对扩散的影响。结果表明：邻居效应或阈值分布均值的减小将加速扩散及增大均衡状态值，阈值分布方差的减小将减缓初始扩散，且满足一定条件下，将加速扩散收尾过程；邻居效应较弱时，度分布异质性的增加将加速初始扩散，反之亦然；邻居效应和阈值分布满足一定条件时，扩散初始速度将呈现出超指数增长；邻居效应、阈值分布或度分布的变化均可使扩散均衡状态值发生跳跃式增长。

创新扩散；社会网络；邻居效应；社会影响；扩散影响率

0　引言

网络结构特征对创新扩散有着重要影响[1-3]，已有大量文献对此进行了研究。如，文献[4]对比了不同网络结构对于反协调决策扩散的影响，发现度分布对全局涌现具有重要影响。文献[5]研究了具有无标度特性的消费者网络中的新产品扩散问题，文献[6]对比了随机网络、小世界网络和无标度网络对具有网络外部性的新产品的扩散问题，文献[7]研究了初始目标群体的选择、小世界效应和聚簇结构对创新扩散的影响，文献[8]研究了两类信息扩散模型中入度与出度相关性对信息扩散率的影响。文献[9]构建了基于SIS模型的平均场扩散过程，利用随机占优理论分析了网络平均度，度分布异质性和“邻居效应”对扩散“相变”的影响，但该文并未分析这些因素对扩散初始速率的影响，也未分析节点异质阈值下的情形。

除网络结构因素外，节点采纳倾向的异质性也影响着扩散。阈值模型是刻画这种异质性的有力模型之一，大量学者基于该模型研究了社会网络中的扩散现象。如，Valente区别了社会网络中的群体阈值模型和局域阈值模型，认为一些行为(如暴力行为)的扩散适用于群体阈值模型，而另一些行为(如避孕措施)的扩散适用于局域阈值模型[10]。文献[11]比较了社会传染，社会影响和社会学习规则下的扩散速率，但该文忽略了网络度分布的调节影响。文献[12]基于平均场过程分析了具有异质阈值的“种子”在不同网络平均度下对最终扩散均衡值的影响。但他们并没有研究具有相同平均值，不同异质性的网络度分布对扩散均衡值的影响，也没有研究度分布和“邻居效应”对扩散初始速度的影响。

针对以上研究的不足，本文综合考虑了邻居效应和异质阈值等因素，基于异质阈值决策模型，利用平均场理论构建了社会网络创新扩散过程。重点回答了以下两方面问题：1)邻居效应、阈值分布和网络度分布如何影响动态均衡；2)邻居效应、阈值分布和网络度分布如何影响扩散过程。

1　假设与模型

1.1社会影响网络

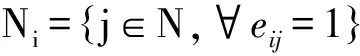
文献[1]和[9]研究了无向网络中的扩散问题，无向意味着节点之间存在着对称关系，但现实生活这种关系往往是不成立的，如Twitter、新浪微博等在线社交网络同时设置了关注与粉丝，允许关注群体与粉丝群体的不一致，因此用不对称关系刻画群体中个体的关系更加合理。

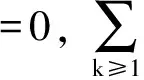
1.2异质阈值模型

阈值模型是解释公共意见形成的重要模型之一，广泛应用于社会网络扩散研究。群体中，低阈值个体更早加入特定行为，高阈值个体则在大部分邻居加入后才决定加入[10]。本质上讲，阈值模型刻画了一类依赖于已加入特定行为的邻居比例进行决策的行为扩散现象，合适的群体异质阈值分布可解释个体层行为到集体层行为(如抢劫、出席会议和吸烟等)的形成[13-15]。

假设节点i有不变的采纳阈值ci，t时刻节点i采纳创新的效用函数为

πi(t)=f(ki,ai(t))-ci

其中：f(ki,ai)表示邻居影响规则，ki为节点i在其局域环境中能受到的最大影响量，ai为目前的已存在的影响量，且有f(ki,0)=0；ci为节点i采纳创新的阈值，不失一般性，假设ci服从截尾的正态分布：

如果πi(t)≥0，那么节点i将考虑采纳创新，即进入决策的下一个阶段，反之则保持未采纳状态。考虑行为惯性和决策变更时间约束等因素的影响，每周期节点依据一定规则进行决策，以λ表示状态的修正概率。因此，在该决策阶段，πi(t)≥0的节点将以概率λ采纳创新。此外将ci=0的节点视为创新者，即邻居中尚无采纳者时，这部分节点可能选择采纳创新。

由以上过程可知，网络中节点采纳状态空间的转变过程与时间无关，只受局域环境f(ki,ai(t))影响。

1.3扩散过程

假设社会群体N足够大，可利用平均场近似方法将局部影响加总，形成影响网络全局的平均场。平均场近似方法作为统计物理中经典近似方法之一，已被复杂网络扩散文献广泛使用[4,9,16-19]。假设度分布和节点邻居数量不变，每周期节点从网络中随机选取一定数目的个体作为邻居，观察他们的采纳行为，决定是否采纳创新。

令ρk(t)表示t时刻度为k的亚群体扩散率，ρ(t)为t时刻群体总扩散率，则：

(1)

其中,0≤ρk(t)≤1，0≤ρ(t)≤1。

(2)

其中,N·〈k〉为网络中的总边数，代表了网络中可能达到的最大扩散影响量，此外，θ(t)∈[0,1)。在该网络中，扩散影响率是由网络度分布和亚群体扩散率构成的综合指标，度分布确定的条件下，扩散影响率和亚群体扩散率呈正比关系，即亚群体扩散率越大，扩散影响率也越大。在本文构建的社会网络中，θ(t)等价于节点任意一条边指向采纳者节点的概率，由此可以得出t时刻度为k的节点所受期望扩散影响量：

进而，可以得到t时刻度为k的亚群体对θ(t)的下一时刻的期望扩散率(下文将之称为θ(t)的“亚扩散率响应函数”)：

(3)

在此基础上，也可得下一时刻的期望扩散影响率(下文将之称为θ(t)的“扩散影响率响应函数”)和总扩散率响应函数：

(4)

t时刻入度为k的亚群体由未采纳状态转变采纳状态的瞬时速率可表示为

(5)

再结合式(2)、(3)和(5)可得扩散影响率和扩散率的瞬时变化率：

(6)

从微观视角出发，节点的状态依邻居规则转变，因此在该动态过程存在着节点状态的逆向转变。

由以上过程可知，给定度分布p(k)和邻居影响规则，若不考虑时间约束，随着扩散影响率θ(t)趋于稳定，扩散最终将以渐进方式达到某个均衡点[11,19]。如果邻居的采纳行为对节点采纳创新具有积极影响，则为趋同选择扩散，反之则为差异化选择扩散[4,20]。本文聚焦于分析趋同选择下的扩散，即邻居影响规则满足：f(k,a+1)-f(k,a)≥0,∀k，并假定邻居影响规则为f(k,a)=a·k-β，1≤β<2，β表示邻居效应。下文将综合利用理论和数值分析结合的方法揭示该社会网络扩散动态过程。

2　理论分析

2.1邻居效应

创新扩散异于病毒扩散的一个重要特性在于节点采纳之前对邻居行为的主动观察，邻居效应刻画了邻居结构对节点创新采纳行为的阻碍作用，在本文中邻居影响规则为f(k,a)=a·k-β，其中β代表了邻居效应，随着它的增大，节点越倾向于对采纳创新持观望态度，进而影响创新的扩散过程和所能达到的均衡状态。

定理1对于度分布p(k)的网络，群体阈值分布均值为μ，方差为σ，邻居影响规则f(k,a)=a·k-β，0≤β≤2，则以下命题成立：

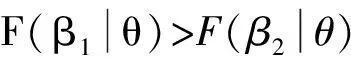
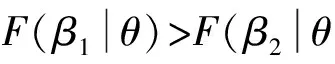
由定理1可知，邻居效应的增强会减少扩散达到的均衡扩散影响率，该结论符合现实，邻居效应等价于群体规范的阻碍效应，对于一个具有前瞻性、创新性的群体，群体规范的阻碍效应相对较弱，因此该群体中创新事物的扩散过程接近于病毒扩散过程；而对于一个因循守旧的群体，旧的群体规范将束缚创新事物在群体中的扩散过程，创新事物也难以达到大规模的扩散。

定理2如果群体阈值分布均值为μ，方差为σ，邻居影响规则f(k,a)=a·k-β，扩新过程为平均场近似过程，当β=1时，对于任意的pa(k)和pb(k)，存在：F1(θ)=F2(θ)

证明：将β=1代入F(θ)可得：

即F(θ)与p(k)无关，因此命题得证。

由定理2可知，由于邻居效应的调节作用，在特定情况下，即使存在着入度很大的节点，网络结构也并不对创新的扩散过程产生影响。这种情况下，入度更大的节点也需要有更多已采纳邻居才会选择采纳创新，因此各亚群体的采纳过程是一直的，从而全局的采纳过程并不会受到度分布的影响。

2.2异质阈值

对于不同的创新或者产品，因其给个体带来的效用或者成本的差异，其群体阈值分布也存在着差异。如一种产品具有相对较低的价格，则阈值分布均值也相应较低，若一种产品具有相对较高的风险，则阈值分布均值相应较高，由于这种变化并不是线性的，因此也可能造成阈值分布方差的变化。下文将分析这两个参数对扩散的影响。

定理3对于度分布为p(k)的网络，阈值分布均值为μ，方差为σ，邻居影响规则f(k,a)=a·k-β，0≤β≤2，则以下命题成立：

(7)

由定理3可知，群体的阈值分布特征对创新扩散过程存在着影响。对于一种创新，其它条件不变的情况下，如果群体1的阈值分布均值大于群体2,，那么创新在群体1中将扩散得更快；类似地，如果群体1的阈值分布方差大于群体2，那么创新在群体2的扩散初始阶段的速度更快，在一定条件下，创新在群体1的扩散完成阶段的速度更快。

2.3网络结构

网络结构决定了节点的局域环境，因此影响着节点的创新采纳决策，本文引入度分布以描述网络结构，并引入随机占优理论中的二阶随机占优、分析度分布异质性对扩散的影响。随机占优理论作为一种不确定性条件下的群体决策方法在经济中被广泛使用，借鉴其原理，文献[4]，[9]和[16]将其引入比较不同度分布下决策函数的期望。下文引入假设：pa(k)是pb(k)的MPS，且平均度为〈k〉。

定理4对于度分布为pa(k)和pb(k)的网络，假如pa(k)是pb(k)的MPS，群体阈值分布均值为μ，方差为σ，邻居影响规则为f(k,a)=a·k-β，kmin≤k≤kmax，0≤β<2，则以下命题成立：

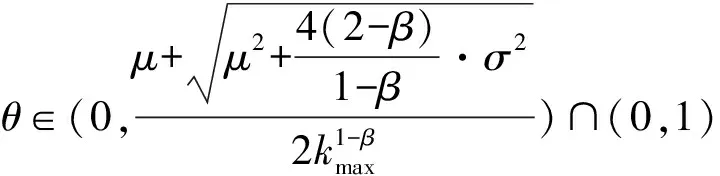
2)若β=1，则对于所有的θ∈(0,1)，Fa(θ)=Fb(θ)；

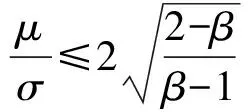
证明：首先对F(θ)求θ的一阶导和二阶导：

令：

不妨假设UF(k;θ)为k的连续函数，对UF(k;θ)求k的二阶导：

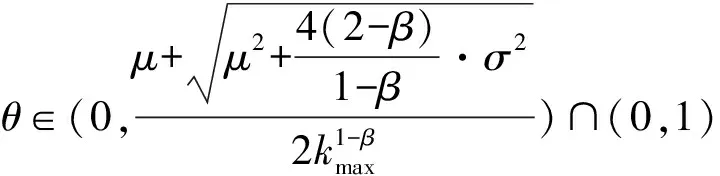
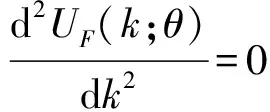
由定理4可知，满意一定条件时，可比较不同网络中的扩散影响率响应值。当0<β<1，在初始阶段的某段时间内，必有Fa(θ)≥Fb(θ)，而在后期可能出现Fa(θ)≤Fb(θ)的情形。当β=1时，度分布异质性并不会对扩散过程产生任何影响。当1<β<2时，如果阈值分布函数和β满足一定关系，在整个过程中将有Fa(θ)≤Fb(θ)，即度分布异质性的提高抑制了扩散过程。由以上分析可知，当0<β<1且满足一定条件时，Fa(θ)与Fb(θ)将相交于一点，原因为：θ较小时，大部分亚群体满足k1-βθ-μ≤0，此时UF(k;θ)满足凸性条件，因此度分布异质性越高，扩散影响率响应值越大；随着θ的增大，UF(k;θ)的凸性被破坏并将出现拐点，但此阶段并不意味着Fa(θ)≥Fb(θ)一定成立；当θ继续增大到特定值时，大部分亚群体将满足k1-βθ-μ>0，此时UF(k;θ)满足凹性条件，因此有Fa(θ)≥Fb(θ)。根据以上分析，度分布异质性影响着扩散影响率加速，因此在给定条件下，可得到利于扩散影响率加速的最优度分布。

推论1对于平均度为〈k〉的网络族，若群体阈值分布均值为μ，方差为σ，邻居影响规则f(k,a)=a·k-β，kmin≤k≤kmax，0≤β<2，则以下命题成立：

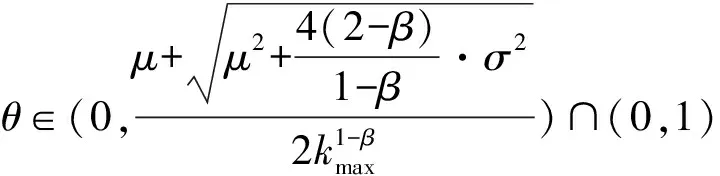
2)若β=1，则对于所有的θ∈(0,1)，网络度分布异质性对扩散影响率增长无影响；

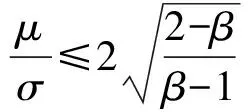
证明：由定理1可反推出本结论。

由推论可知，根据条件，最优网络度分布有两种，第1种为所有节点为最小度或者最大度，第2种为所有节点的度都在平均度附近。第1种度分布代表了度分布最大异质性，即链接在节点之间的不均衡分配；第2种度分布代表了度分布最小异质性，即链接在节点之间的相对均匀分配。

网络度分布异质性影响了扩散影响率趋向的均衡值，而扩散影响率是随时间演进的，因此该影响必然体现于扩散过程中。扩散过程可由扩散影响率、扩散影响率增长速度和加速度描述，因此以下分析将围绕度分布异质性对扩散影响率的影响展开。

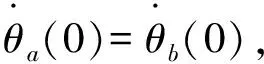
在扩散的初始时刻：

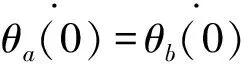
由定理5可知，度分布异质性与邻居效应共同决定了初始扩散影响率加速度。如果邻居效应较弱(0≤β<1)，且创新只能在群体很小范围内扩散，随着度分布异质性的增大，创新越容易在群体中扩散，反之则可能只在群体较小范围内使用。因此，如果创新在规则网络中只能达到很低的扩散影响率，随着度分布异质性的增大，可能产生二阶相变现象，即扩散影响率在经过初始阶段的低速增长后，迅速增至较大的值，其它条件不变的情况下，二阶相变的度分布异质性临界值应满足：

其中,ϑ(t)为扩散影响率的相对加速度，再求其t的一阶导：

则ϑ(t)为原点附近的严格减函数，若μ≤0，则对于任意度分布异质性的网络，扩散初始阶段的扩散影响率呈现亚指数增长。

定理6给定网络度分布p(k)与平均度〈k〉，阈值分布均值μ>0，方差为σ，邻居影响f(k,a)=a·k-β,0≤β<1，则以下陈述成立：

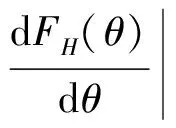
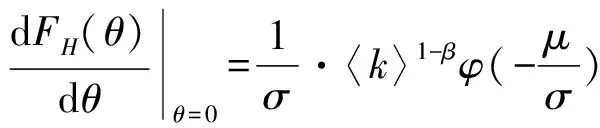
定理6表明，在邻居影响规则f(k,a)=a·k-β,0≤β<1下的初始阶段影响率增长可能出现的两种特性：减速增长或超指数增长，且度分布异质性对减速增长有削弱效果，对超指数增长则有放大效果。对于具有相同平均度的无标度网络、指数网络和规则网络，初始阶段无标度网络中扩散可能呈现出超指数增长，而其它网络却无显著扩散。其原因在于异质网络中初始阶段有更大比例的大入度节点采纳创新，因此扩散影响率增长速度更大。

3　数值分析

不同邻居效应、阈值分布和度分布的社会网络扩散具有不同的特性，其中扩散所能达到的均衡状态是学者们关注的重要方面之一。为此，本小节着眼于回答如下问题：在一定的邻居效应和异质阈值分布下，度分布对创新扩散均衡状态有何影响？已有文献利用一阶和二阶随机风险占优理论回答了类似问题[4，19]，但其前提条件过于苛刻，如，在定义域内风险函数的凹性和凸性，度分布密度函数之间的风险占优关系等等。此外，均值或方差只是刻画密度分布函数的关键指标之一。然而，社会网络扩散内在复杂性难以保证这些前提条件，因此也难以对邻居效应、阈值分布、度分布与扩散均衡状态之间的关系下定论。为了弥补这个不足，本小节在前文建立的动态扩散过程基础上，结合实际确定了合适的参数范围，进行了大量的数值模拟，以更直观地呈现它们之间的关系。值得注意的是，以下分析聚焦于讨论最小均衡点，即无外部驱动力作用下，创新在群体中的潜在扩散范围。

根据创新扩散理论，在创新进入群体的初始阶段，少量创新者无需参照他人的行为进行采纳决策，并认为创新者占群体的比例为2.5%。另外，根据文献[7]，对于技术创新产品，存在一定比例的“发烧友”，这部分人的采纳决策也无需参照他人的行为，且该文将“发烧友”的比例设定为群体的2.5%。由于本文的目的在于呈现度分布对于均衡状态的影响，本文将初始采纳率适当进行放大，设置为21.2%。

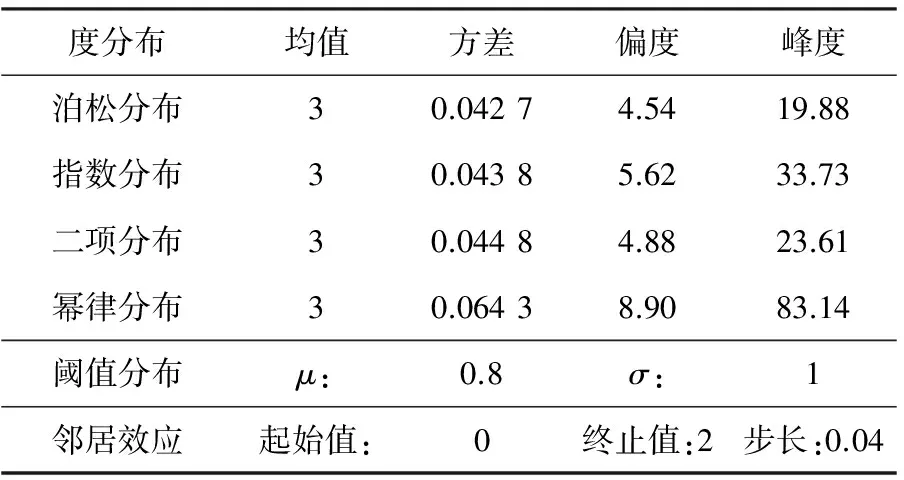
表1　参数设置

此外，分别取范围为1≤k≤99的度分布密度函数为(或近似为)：泊松分布、指数分布、二项分布和幂律分布。从0至2间隔0.04对β分别取值，最终计算出阈值分布和度分布密度函数下，邻居效应值对应的均衡ρ*，具体参数参照表1。此外，本文基于平均场近似方法得出扩散过程，而平均场近似中的网络结构是动态变化的。然而，大部分现实世界网络在一定时期内都是固定不变了。因此，其它条件保持的情况下，本节构建仿真程序探索了固定网络中的扩散均衡。其中，固定网络基于配置网络生成算法产生，对应为平均场过程的度分布。这些分布函数的自变量均为从1到99的整数，因此它们为对应分布函数的近似，该方法参照文献[9]。此外，均衡值为对应10次仿真的平均。图1a，2a和3a为平均场过程下的均衡值，图1b,2b,3b为仿真过程的均衡状态。

本文数值分析的目的在于揭示参数对各分布下均衡状态的影响，由于它们之间的影响关系较为复杂，难以直接从静态的数值关系中得出结论，因此本文选用关键的图形以更加直观地呈现这种关系。图1为阈值分布为μ=0.8,σ=1的情形，从中可观察到度分布、邻居效应和均衡状态之间有以下关系：1)各度分布下的均衡状态值ρ*均随β增大而减小，这与定理1一致；2)当β在0附近时，各度分布下的均衡值由大到小依次为：二项分布、泊松分布、指数分布和幂律分布。但随着β增大至1，这种关系将向相反方向转变。3)虽然不同的度分布之间满足二阶风险占优关系，但并不能据此得到0≤β<2下的均衡状态大小关系的一般规律，如指数分布是泊松分布的MPS，二项分布是指数分布的MPS，但指数分布的均衡值并不介于泊松分布和二项分布之间。此外，通过计算各度分布的峰度和偏度可知，各度分布在大部分β下的均衡值大小关系和偏度、峰度的排序一致。4)对比平均场和仿真情况可以发现，两者在不同β下的均衡值大致相等，且大部分β下各度分布的均衡值的关系基本保持一致。

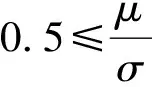
3.1阈值分布均值的影响

固定σ=1，μ从0.5至2之间均匀取值，步长为0.025，然后计算各组(μ,σ)下不同度分布对于β的均衡状态，可观察到上述3个结论在0.5≤μ≤1.25时仍然成立。但是，随着μ的增大，部分结论将不再成立。

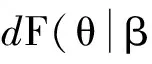
此外，从图2可以发现，当所有分布下的均衡值在β=0均下降至较小值，且β在0附近时，各度分布下的均衡值由大到小依次为：幂律分布、指数分布、泊松分布和二项分布。同样的，这些关系与仿真过程结论一致，即存在着均衡值的突然增加。不过，在β=0附近，这种关系被破坏，可能原因在于柏松和二项分布。

3.2阈值分布方差的影响

固定μ=0.8，σ从0.2至1.6之间均匀取值，步长为0.05，然后计算各组(μ,σ)下不同度分布对于β的均衡状态。总体而言，σ的调节影响与β恰好相反，即在一定范围内，以上4个结论均成立，但是，随着σ的减小，部分结论不再成立，如图3，σ的减少同样导致了均衡值的跳跃性变化，而且这种跳跃性变化也将改变各分布下均衡值的大小关系。

通过以上分析发现，调节邻居效应、阈值分布和度分布，可使扩散发生二阶相变，即创新在群体小范围中经历缓慢增长之后，突然扩散至群体较大范围。该结论可解释为何一些创新可在群体中扩散至较大范围，而另一些却扩散失败。因此，根据以上分析，在考虑群体影响特性的基础上，可通过改变群体阈值，如降低成本或增强创新的非外部性功能，使创新的均衡状态值跳跃至一个较大比例。

4　结论

本文建立了包含网络度分布和异质阈值的创新扩散模型，基于此分析了度分布异质性与邻居效应对扩散均衡和初始阶段扩散的影响，结果表明：1)当邻居效应较小时(0≤β<1)，度分布异质性越大，创新越容易在群体内较大范围扩散，且随着度分布异质性的提高，可能引发扩散中的“二阶相变”现象；初始增长可能呈现两种方式：减速增长与超指数增长，度分布异质性的提高会抑制减速增长现象，度分布异质性满足一定条件下初始阶段影响率呈现指数或超指数增长，而度分布异质性的增大同样会促进影响率的超指数增长；2)当β=1时，度分布异质性对扩散过程不产生任何影响；3)当邻居效应较大时(1<β<2)，度分布异质性的提高反而会抑制扩散风险率的增长，且会降低初始阶段的扩散风险率增长速度。此外，通过数值模拟发现均衡扩散率受邻居效应、阈值分布和度分布的共同影响，且三者均可使扩散发生二阶相变现象。最后，通过复杂网络仿真实验验证了解析结论。

本研究结论可为企业的营销活动提供参考，邻居效应在扩散中起着重要影响，但应视其强度制定具有针对性的营销策略。

[1]Boccaletti S, Latora V, Moreno Y, et al. Complex networks: structure and dynamics[J]. Physics Reports, 2006, 424 (4/5): 175-308.

[2]Newman M E J. The structure and function of complex networks[J]. SIAM Review, 2003, 45(2): 167-256.

[3]Centola D.The spread of Behavior in an online social network experiment[J]. Science, 2010, 329: 1194-1197.

[4]赵正龙, 陈忠, 孙武军, 等. 具有差异化选择特征的复杂社会网络扩散研究[J]. 管理科学学报, 2010, 13 (3): 38-48.

Zhao ZhengLong, Chen Zhong, Sun WuJun, et al. Diffusion with property of differential choice in complex social network[J]. Journal of Management Sciences in China, 2010, 13(3):38-48.

[5]Duan W, Chen Z, Liu Z. Efficient target strategies for contagion in scale-free networks[J]. Physical Review E, 2005, 72(2): 26-133.

[6]段文奇, 陈忠. 网络效应新产品成功的关键: 产品质量还是安装基础? [J]. 系统工程理论与实践, 2007, 23(7): 144-148.

Duan WenQi, Chen Zhong. Key factor to drive success of new product with network effects: product quality or installed base? [J]. System Engineering Theory&Practice, 2007, 23(7): 144-148.

[7] Choi H, Kim S H, Lee J. Role of network structure and network effects in diffusion of innovations[J]. Industrial Marketing Management, 2010, 39(1): 170-177.

[8]Ohara K, Kazumi S, Masahiro K, et al. Effect of in/out degree correlation on influence degree of two contrasting in formation diffusion models[C]. SBP 2012, LNCS 7227: 131-138.

[9]Lopez-Pintado D. Diffusion in complex social networks[J]. Games and Economics Behavior, 2008, 62(2): 573-590.

[10] Valente T W. Social network thresholds in the diffusion of innovations[J]. Social Networks, 1996, 18: 69-89.

[11] Young H P. Innovation diffusion in heterogeneous populations:contagion,social influence,and social learning[J]. American Economic Review, 2009, 99(5): 1898-1924.

[12] Gleeson J P, Cahalane D J. Seed size strongly affects cascades on random networks[J]. Physical review E, 2007, 75, 056103.

[13] Granovetter M. Threshold models of collective behavior[J]. American Journal of Sociology, 1978, 83: 1420-1443.

[14] Granovetter M, Song R. Threshold models of interpersonal effects in consumer demand[J]. Journal of Economic Behavior and Organization, 1986, 7: 83-89.

[15] Macy M W. Chains of cooperation:threshold effects in collective action[J]. American Sociology Review, 1991, 56: 730-737.

[16] Lopez-Pintado D. Influence networks[J]. Games and Economics Behavior, 2012, 75: 776-787.

[17] Pastor-Satorras R,Vespignani A. Epidemic dynamics and endemic states in complex networks[J]. Physical Review Letters, 2000, 86(24): 3200-3203.

[18] Dodds P S, Watts D J. Universal behavior in a generalized model of contagion[J]. Pyhsical Review Letters, 2004, 92(21), 218701.

[19] Jackson M O,Yariv L. Diffusion of behavior and equilibrium properties in network games[J]. American Economic Review, 2007, 97(2): 92-98.

[20] Yann B. Anti-coordination and social interactions[J]. Games and Economic Behavior, 2007, 58: 30-49.

(责任编辑李进)

Modeling Heterogenous Threshold Rule Based Innovation Diffusion

XIAO Yu1, HAN Jingti2

(1.School of Business Information, Shanghai University of International Business and Economics, Shanghai 201620, China;2.a.School of Information Management and Engeneering， b.Experimental Center, Shanghai University of Finance and Economics, Shanghai 200433, China)

Based on heterogenous threshold model and mean-field theory, we analyse the impact of neighbor effect, threshold distribution and degree distribution on the diffusion process and equilibrium. The result shows that the decrease in neighbor effect or the mean of threshold distribution would speed up the diffusion process and increase the equilibrium value. Besides, the decrease in the variance of threshold distribution would slow down the initial diffusion process, and would also speed up the end-stage diffusion when some conditions are given; if the neighbor effect is low, the increase in the heterogeneity of degree distribution would speed up the initial diffusion stage; the initial diffusion would experience a super-exponential increase stage when a certain relationship between the neighbor effect and the threshold distribution is met; the change in neighbor effect, threshold distribution or degree distribution may lead to a jump increase of the equilibrium value.

innovation diffusion; social network; neighbor effect; social influence; diffusion-Influence rate

1672-3813(2016)03-0047-11;DOI:10.13306/j.1672-3813.2016.03.007

2014-11-17；

2015-12-18

国家自然科学基金(71271126)；教育部博士点专项科研基金(20120078110002)；上海财经大学第六批研究生科研创新基金(CXJJ-2012-427)；教育部人文社会科学研究规划基金(15YJCZH201)；上海市教育委员会科研创新项目(14YZ134)

肖宇(1986-)，男，江西宁都人，博士，讲师，主要研究方向为创新扩散和社会网络。

韩景倜(1959-)，男，陕西西安人，博士，教授，主要研究方向为复杂系统理论、应急管理。

F244

A