用柱状成层各向异性介质的并矢Green函数模拟多分量感应测井仪器的响应

魏宝君,王成园,党　峰,常欣莉,曹景强

(1.中国石油大学理学院,山东青岛 266580; 2.中国石油大学山东省高校新能源物理与材料科学重点实验室,山东青岛 266580; 3.中国石油集团测井有限公司,陕西西安 710077)



用柱状成层各向异性介质的并矢Green函数模拟多分量感应测井仪器的响应

魏宝君1,2,王成园1,党峰3,常欣莉1,曹景强1

(1.中国石油大学理学院,山东青岛 266580; 2.中国石油大学山东省高校新能源物理与材料科学重点实验室,山东青岛 266580; 3.中国石油集团测井有限公司,陕西西安 710077)

采用递推方法得到柱状成层各向异性介质(横向各向同性)中并矢Green函数的解析表达式。该表达式可用于模拟柱状成层各向异性地层中任意点源(包括电流源和磁流源)的响应,地层数目可以任意,源点和场点的位置可以在任意地层中。利用上述表达式模拟含金属心轴和绝缘保护层多分量感应测井仪器在有井眼和侵入带各向异性地层中的响应。为提高模拟精度,考虑各分量线圈系的具体形状。将金属心轴作为一层介质处理,既可以考虑其电导率有限，也可以考虑其电导率为无穷大的情况。数值模拟结果表明,共面线圈系具有与共轴线圈系完全不同的响应特性。共面线圈系的响应特性更为复杂,对钻井液电导率、侵入带电导率、地层电导率、地层各向异性的变化更为敏感,且在很多情况下其响应会随这些参数的变化出现符号改变。此外,由于共面线圈系的同一响应可对应各向同性地层或各向异性地层的不同电导率,从而使得对测量数据的解释处理变得复杂。

多分量感应测井; 并矢Green函数; 柱状成层各向异性介质; 金属心轴; 侵入带

引用格式:魏宝君,王成园,党峰,等.用柱状成层各向异性介质的并矢Green函数模拟多分量感应测井仪器的响应[J].中国石油大学学报(自然科学版),2016,40(2):59-69.

WEI Baojun,WANG Chengyuan,DANG Feng,et al.Simulating responses of multi-component induction logging tools by dyadic Greens functions in cylindrically stratified anisotropic media[J].Journal of China University of Petroleum(Edition of Natural Science),2016,40(2):59-69.

感应测井是一种重要的井中电阻率测量技术。传统的感应测井仪器一般采用一组或多组共轴发射-接收线圈阵列,只能提供井眼周围的横向电导率信息。然而,一些实际地层如砂-泥岩薄交互层的宏观电参数是各向异性的,即横向电导率和垂向电导率不同,从而形成横向各向同性(TI)地层[1]。传统感应测井仪器所获得的测量数据并不能反映井眼周围这类地层的真实特性,给地层的精确评价带来误差。多分量感应测井仪器由一组或多组沿3个方向彼此垂直的发射-接收线圈阵列组成,可同时测量感应电动势的9个分量,从而能探测到各向异性地层的横向电导率和垂向电导率信息,对复杂地层的高精度对比评价具有重要意义[2-3]。井眼、侵入、地层各向异性、仪器结构等因素对多分量感应测井响应均产生影响[1-3],系统地分析这些因素的影响规律对测量数据的解释处理具有重要价值。由于有限差分和有限元等数值模拟方法在分析此类问题时效率低、速度慢[4],因而选取合适的、能存在解析解的模型并采用高效的解析方法进行模拟是最佳选择。事实上,在分析井眼中各类电磁测井仪器的响应特性、分析仪器在柱状成层或水平成层地层中的响应特性、模拟仪器的刻度时多采用解析方法[4-14]。笔者基于圆柱坐标系下均匀各向异性介质中并矢Green函数的矢量本征函数展开式,采用递推方法[6]得到柱状成层各向异性介质中并矢Green函数的解析表达式,在推导过程中将金属心轴作为一层介质处理,既可以考虑其电导率有限，也可以考虑其电导率为无穷大的情况。利用上述表达式模拟分析钻井液电导率、侵入带电导率、地层电导率、地层各向异性等因素对含金属心轴和绝缘保护层多分量感应测井仪器响应的影响规律,为提高模拟精度考虑各分量线圈系的具体形状。

1　基本理论

1.1均匀各向异性介质中谱域电磁场纵向量与横向量之间的关系

采用圆柱坐标系并假设发射源随时间的变化关系为exp(-iωt),其中ω为角频率。在圆柱坐标系中,,其中,并令E=Es+ezEz、H=Hs+ezHz,则在无源区域中由Maxwell方程组得

(1)

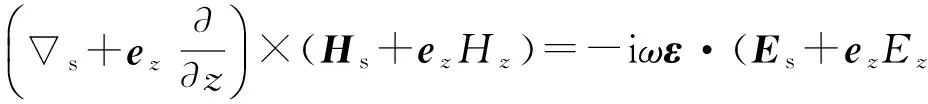
(2)

其中

ε=diag(εh,εh,εv).

式中,ε为横向各向同性(TI)地层介电常数张量，εh和εv分别为其水平和垂直分量。将式(1)和(2)展开并考虑到等式两侧场的纵向分量和横向分量分别相等,经推导可将电磁场的横向分量用纵向分量表示为

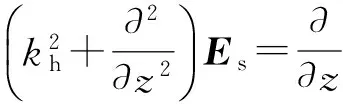
(3)

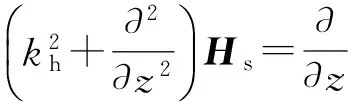
(4)

其中

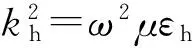
考虑到频率域电磁场均可表示为谱域电磁场积分的形式[15],即

(5)

(6)

(7)

即均匀各向异性介质中谱域内电磁场的横向分量可用纵向分量表示。

1.2均匀各向异性介质中谱域磁流源并矢Green函数

假设ρ>ρ′,对比均匀各向同性介质中谱域磁流源并矢Green函数的矢量本征函数展开式的各分量[16],考虑到沿z方向单位磁偶极子源只产生TE波,其z分量为

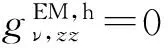
(8)

(9)

沿ρ方向单位磁偶极子源既产生TE波，又产生TM波,其z分量为

(10)

(11)

其中

式中,K为各向异性系数。

沿φ方向单位磁偶极子源既产生TE波，又产生TM波,其z分量为

(12)

(13)

考虑到式(6)、(7),定义如下矩阵:

(14)

(15)

(16)

则在ρ>ρ′时,均匀各向异性介质中谱域磁流源并矢Green函数的所有分量可表示为

(17)

(18)

(19)

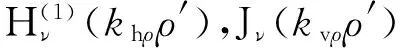
1.3均匀各向异性介质中谱域电流源并矢Green函数

当ρ>ρ′时,对比均匀各向同性介质中谱域电流源并矢Green函数的矢量本征函数展开式的各分量[16],考虑到沿z方向的单位电偶极子源只产生TM波,其z分量为

(20)

(21)

沿ρ方向单位电偶极子源既产生TE波，又产生TM波,其z分量为

(22)

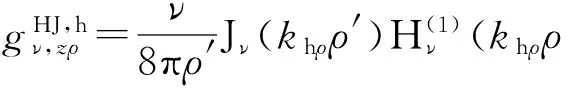
(23)

沿φ方向单位电偶极子源既产生TE波，又产生TM波,其z分量为

(24)

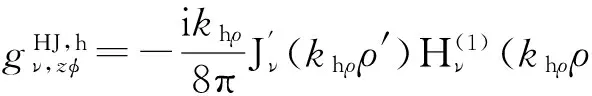
(25)

考虑到式(6)、(7),则在ρ>ρ′时,均匀各向异性介质中谱域电流源并矢Green函数的所有分量可表示为

(26)

(27)

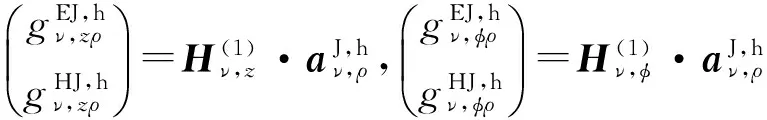
(28)

在谱域内无论是电流源还是磁流源,其沿不同方向的单位源在所有3个正交方向产生的电磁场(即并矢Green函数)的表达式可以统一表示为如下形式:

(29)

(30)

(31)

结合式(5),频率域内不同类型和尺寸的源产生的电磁场可表示为

(32)

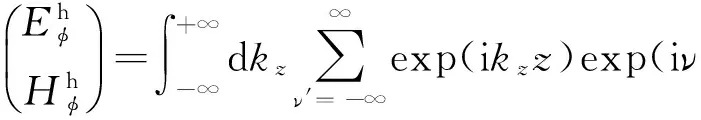
(33)

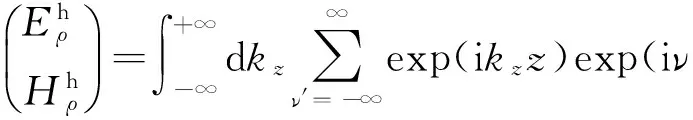
(34)

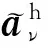
1.4柱状成层各向异性介质中谱域并矢Green函数

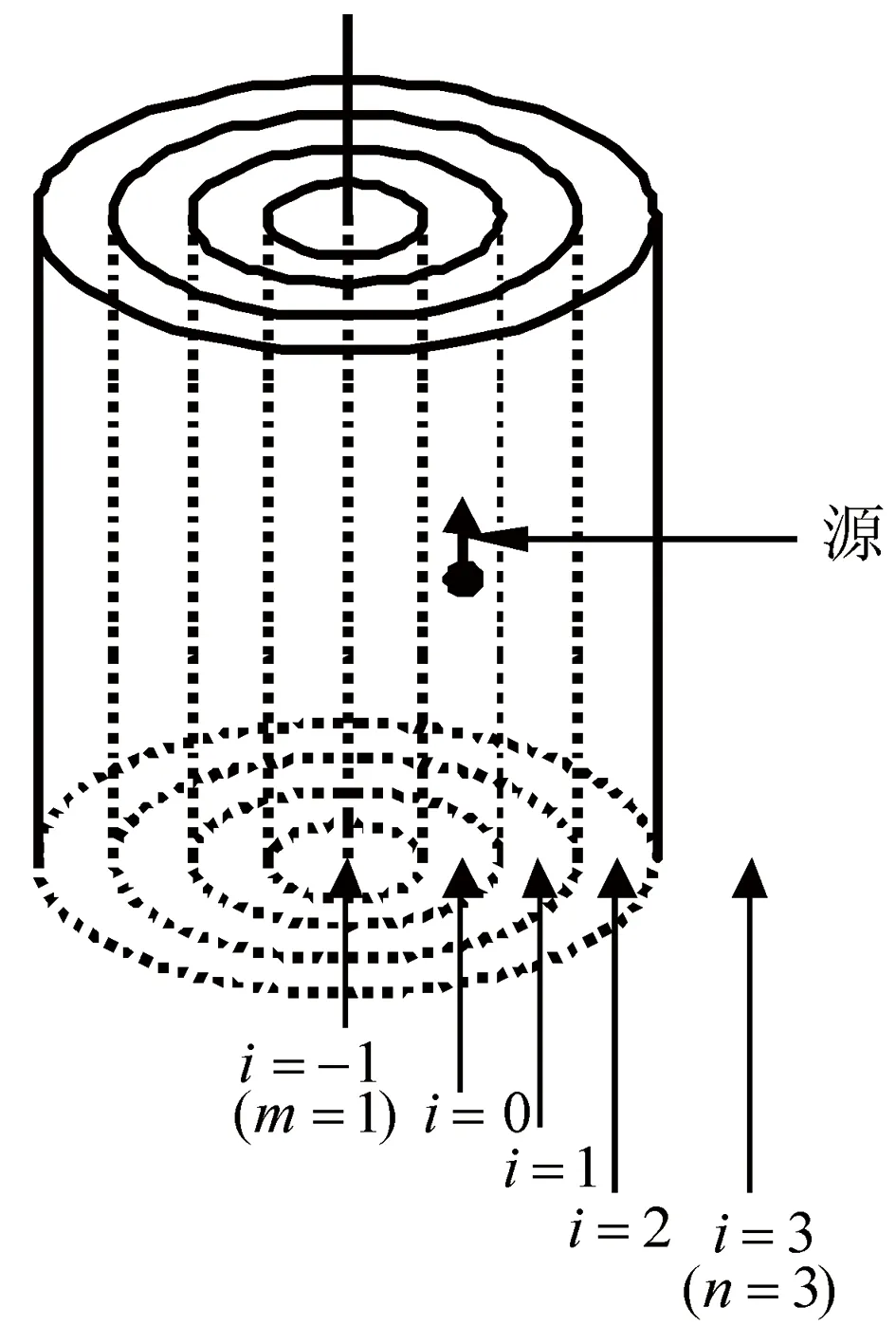
图1　柱状成层各向异性介质模型Fig.1　Model of cylindrically stratified anisotropic media

对于沿ρ方向柱状成多层介质(图1),设介质从里向外编号为-m,-m+1,…,0,1,…,n,半径分别为ρ-m,ρ-m+1,…,ρ0,ρ1,…,ρn-1,源在第0层,类比式(29)～(31)可写出任意第i层介质中谱域并矢Green函数的z分量、φ分量和ρ分量,

(35)

(36)

(37)

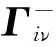
假设有一幅度为aν的电磁波从第i+1层介质向里入射到界面ρi上,该波在ρi处被反射和透射。根据电磁场z分量和φ分量的连续性条件,有

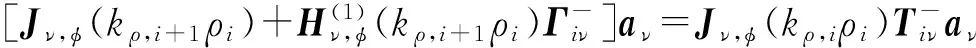
(38)

其中

(39)

(40)

其中

Jν,φ(kρ,iρi).

(41)

再假设有一幅度为aν的电磁波从第i层介质向外入射到界面ρi上,该波在ρi处被反射和透射。根据电磁场z分量和φ分量的连续性条件,有

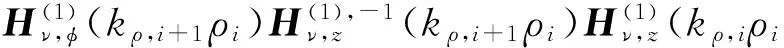
(42)

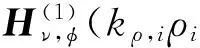
(43)

利用下列递推公式可得到源内侧i≤0所有层的Miν[6]:

(44)

利用式(44)从M-m,ν=0开始递推,一直到M0,ν。

特别地,若最内层介质为理想导体,为满足在ρ=ρ-m处电场z分量和φ分量为0,由式(35)、(36)得

M-m+1,ν=Γν=

(45)

递推时从M-m+1,ν开始,一直到M0,ν。

利用下列递推公式可得到源外侧i>0所有层的Niν[6]:

(46)

利用式(46)从Nnν=0开始递推,一直到N0ν。

尚有列向量aiν、biν需要确定。在第0层,根据式(35)有

(47)

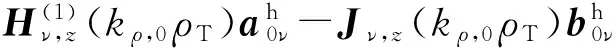
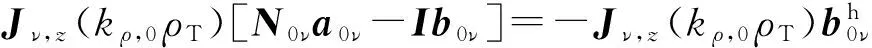
即

(48)

利用式(48)可确定列向量a0ν、b0ν,若利用φ分量或ρ分量所满足的场的阶跃变化条件可得到与式(48)完全相同的形式。确定列向量ai+1,ν、biν可由下式递推[6]:

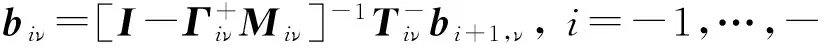
(49)

(50)

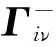
由式(35)～(37)并结合式(5),任意第i层介质中频率域内不同类型和尺寸的源产生的电磁场可表示为

(51)

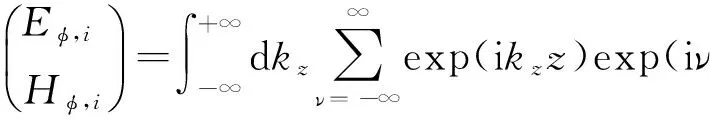
(52)

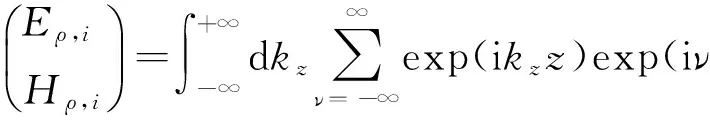
(53)

2　多分量感应测井仪器的响应

2.1z向发射线圈的响应

设z向发射线圈中心点轴向坐标为zT、线圈半径为ρT,发射线圈沿轴向均匀排列在宽度为ΔzT的圆柱面上。z向接收线圈中心点轴向坐标为zR、线圈半径为ρR,接收线圈沿轴向均匀排列在宽度为ΔzR的圆柱面上。扇面形x或y方向接收线圈中心点坐标为(ρR,φR,zR)、轴向宽度为ΔzR、张角为ΔφR。考虑到发射线圈电流源只沿eφ方向,对发射电流源所在的圆柱面形空间进行积分,得

(54)

z向接收线圈处的感应电动势为

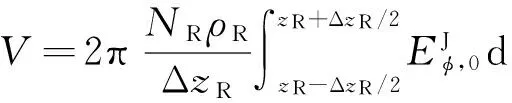
(55)

x或y方向接收线圈处的感应电动势为

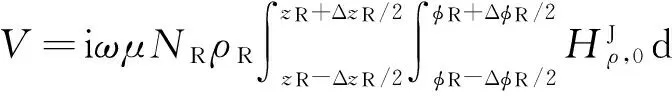
(56)

2.2x或y向发射线圈的响应

设扇面形x或y方向发射线圈中心点坐标为(ρT,φT,zT)、轴向宽度为ΔzT、张角为ΔφT,该类型发射线圈产生的电磁场可以看作是许多沿eρ方向磁偶极子单元产生的电磁场的叠加。对发射源所在的扇面形空间进行积分,得

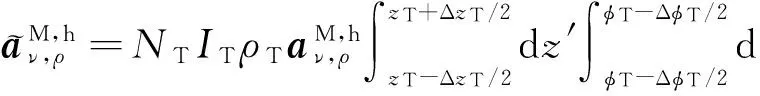
exp(-ikzz′)exp(-iνφ′).

(57)

由于发射线圈和接收线圈均在第0层介质中,电磁场包含背景项,式(51)～(53)的无穷限积分收敛速度较慢。为加快其收敛速度,可根据式(32)～(34)在式(51)～(53)的展开形式中扣除掉背景项,从而得到电磁场及接收线圈处感应电动势的散射项,而背景项部分可单独由发射线圈在各向异性均匀介质中产生的电磁场的辐射积分形式得到。

3　数值算例及讨论

模拟含金属心轴和绝缘保护层的多分量感应测井仪器在有井眼和侵入带各向异性地层中的响应。模拟时采用柱状成5层介质模型,第-1层为金属心轴,第0层为绝缘层,第1层为井眼,第2层为侵入带,第3层为均质各向异性地层。假设发射线圈电流IT=1 A,金属心轴电导率σ-1=2.9×107S/m,半径ρ-1=0.015 m,绝缘保护层半径ρ0=0.045 m,井眼半径ρ1=0.1 m。主要模拟共面线圈系产生的xx分量和共轴线圈系产生的zz分量这两个主分量的感应电动势,每个分量均包含多个具有不同线圈距的子阵列。

3.1多分量感应测井响应与钻井液电导率的关系

忽略侵入带的存在,均质各向异性地层的水平电导率为σht=0.2 S/m,垂直电导率分别取σvt=0.02 S/m和σvt=0.05 S/m两种数值。井眼内钻井液电导率σm从0.001 S/m连续增加到20 S/m。图2给出了4组zz分量线圈系、两组xx分量线圈系的响应随钻井液电导率σm的变化关系,由于zz分量的响应与地层垂直电导率σvt的取值无关,两种情况下的结果完全相同,故图2(a)、图2(b)只给出了一种情况下的结果。对于zz分量,亦用文献[13]的方法进行了模拟,计算结果完全一样,说明了本文推导结果的正确性。

由图2(a)、 (b)可见,当σm较小时,4组zz分量线圈系实、虚部感应电动势的绝对值均随σm的增大而变化缓慢,受地层电导率的影响相对较大,受σm的影响相对较小。随着σm的继续增加,线圈距最短的第一组线圈系由于受井眼影响最大,其响应增加明显,而线圈距越长的线圈系由于受井眼影响越小,其响应改变越不明显。由图2(c)和图2(d)可见,xx分量线圈系的实、虚部响应随σm的变化较zz分量线圈系复杂。当σm处于数值较小的范围时,xx分量线圈系的感应电动势受各向异性地层电导率的影响相对较大,受σm的影响相对较小,故随σm变化的速度较缓慢。当然,σm的具体范围因不同的线圈系、同一线圈系的实部或虚部响应、不同的地层电导率而不同。随着σm的继续增加,xx分量线圈系的实、虚部响应出现快速变化,甚至出现符号的改变。由于随着σm的增加，井眼的影响逐渐增大,各向异性地层电导率的影响逐渐变弱,同一线圈系在不同电导率各向异性地层中的响应趋于一致。对比图2(c)和图2(d)可以发现,实部响应较虚部响应更快地趋于一致。

3.2多分量感应测井响应与地层电导率的关系

仍忽略侵入带的存在,取井眼内钻井液电导率σm=1 S/m,保持均质各向异性地层水平电导率与垂直电导率的比值σht/σvt=5不变,水平电导率σht从0.001 S/m连续增加到20 S/m。图3给出了4组zz分量线圈系、两组xx分量线圈系的响应随地层水平电导率σht的变化关系。为了进行对比,图3(c)、图3(d)同时给出了两组xx分量线圈系在均质各向同性地层中的响应。由于zz分量的响应与地层垂直电导率σvt的取值无关,两种情况下的结果完全相同,故图3(a)、图3(b)只给出了一种情况下的结果。

由图3(a)和图3(b),zz分量线圈系的线圈距越短,其实、虚部响应受井眼影响越大,在地层电导率较小时随σht变化得越缓慢。其后随着σht的继续增加,所有线圈系的响应均增加。由图3(c)和图3(d),无论是在各向同性地层还是在各向异性地层中,xx分量线圈系的实、虚部响应均随σht呈现复杂的变化关系。当σht较小时,xx分量线圈系的感应电动势受井眼电导率的影响相对较大,随σht变化得较缓慢,且同一组线圈系在各向同性地层和各向异性地层中的响应相同。随着σht的继续增加,地层电导率的影响逐渐增大,同一组线圈系在各向同性地层和各向异性地层中的响应出现明显差异。由图3(c),随着σht的增加,第一组短线圈距线圈系实部响应(为正值)出现先减小后增加的现象,甚至在均质各向同性地层中减小到负值,而第二组长线圈距线圈系实部响应(为正值)出现先减小后增加再减小的复杂变化。由图3(d),随着σht的增加,两组线圈系虚部响应出现从正值减小到负值后沿反方向增加再减小的复杂现象。尽管xx分量线圈系的实、虚部响应随σht的变化关系复杂,但同一组线圈系在各向同性地层和各向异性地层中响应的变化规律一致。xx分量线圈系的响应与σht之间的这种复杂关系为该分量的数据解释带来困难,因为同一响应可对应不同的地层电导率。

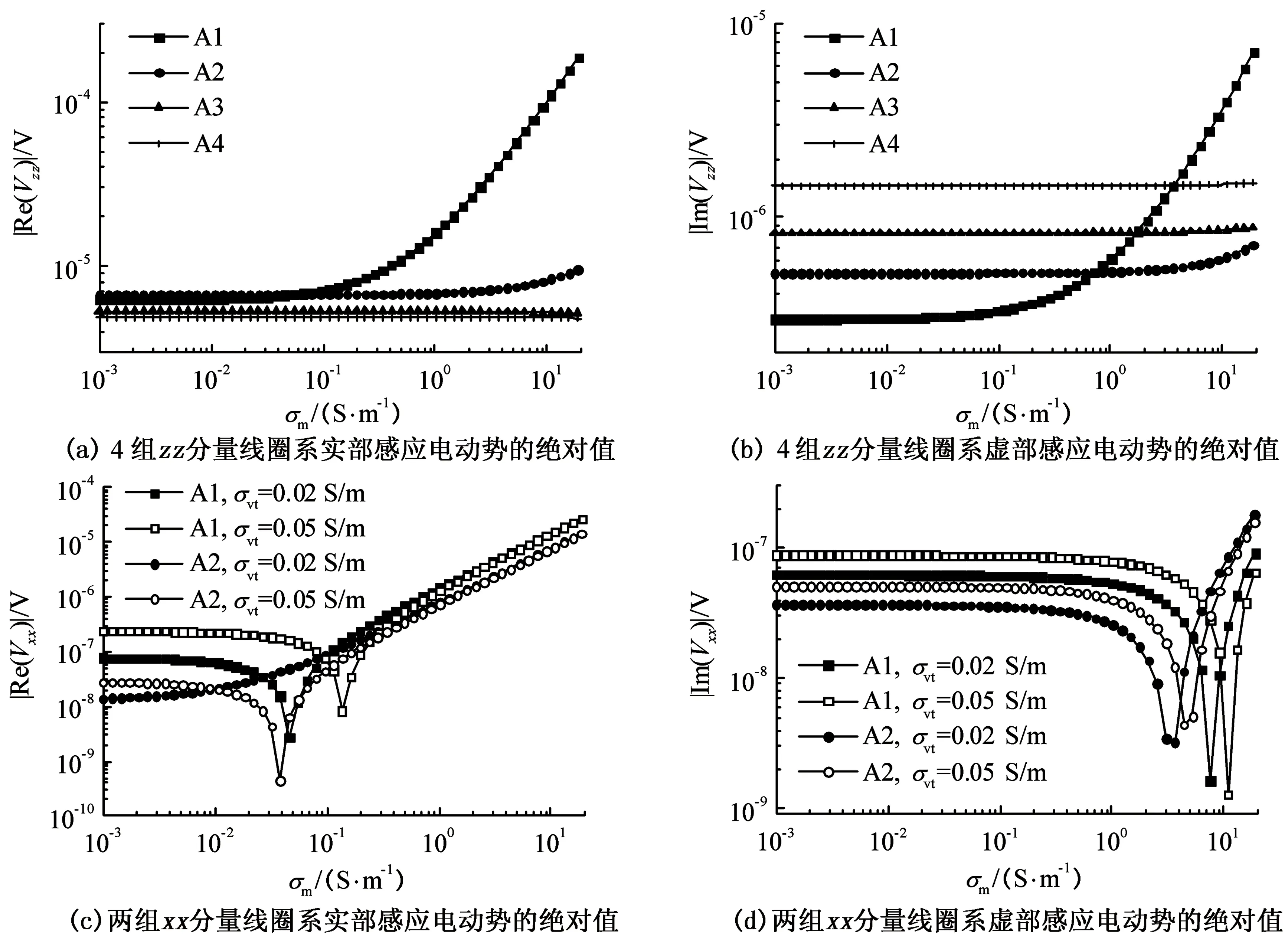
图2　钻井液电导率连续变化时的响应Fig.2　Responses with drilling liquid conductivity continuously varying

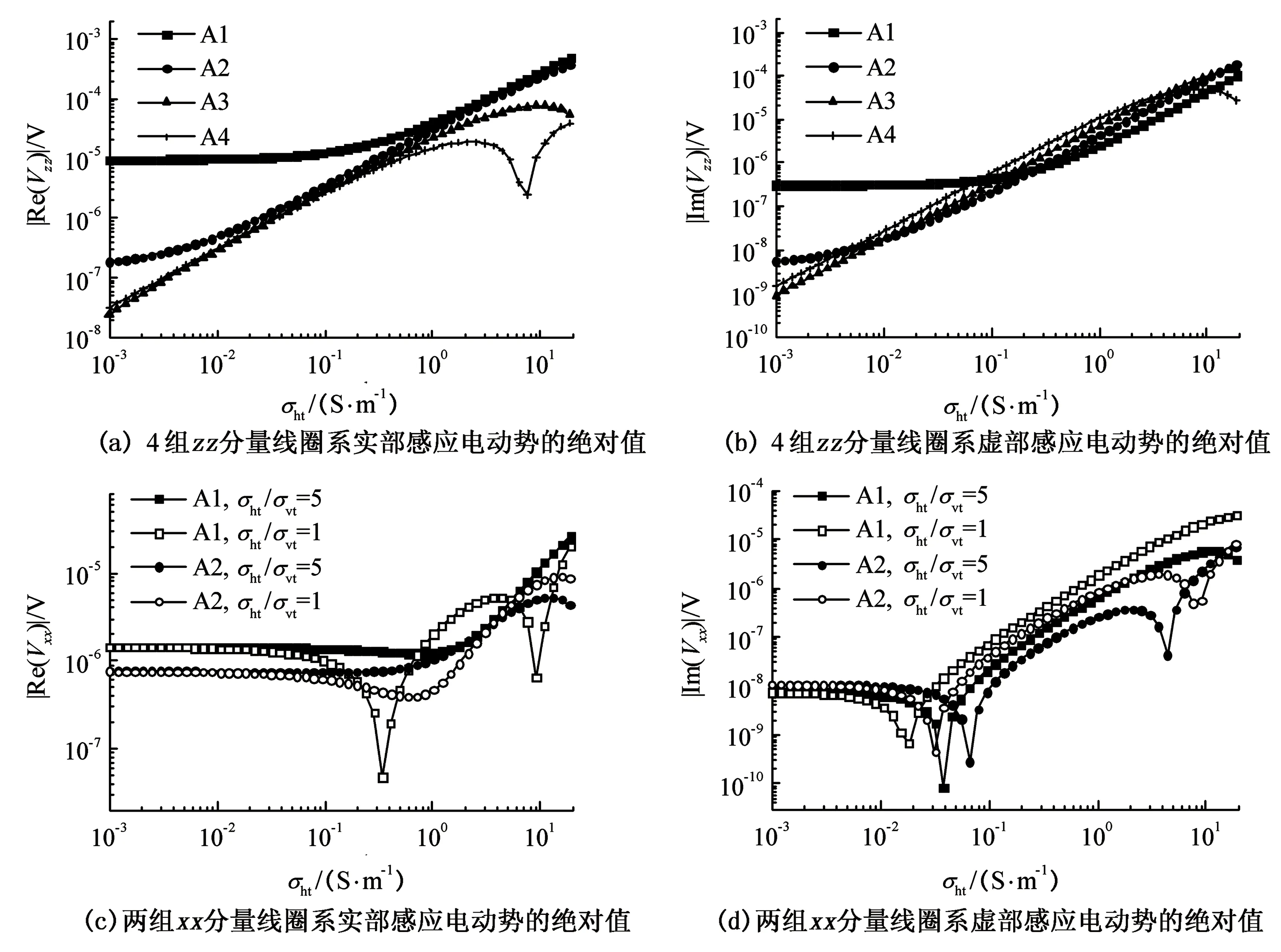
图3　地层电导率连续变化时的响应Fig.3　Responses with formation conductivity continuously varying

3.3多分量感应测井响应与侵入带电导率的关系

假设侵入带半径ρ2=0.5 m,取井眼内钻井液电导率σm=1 S/m,均质各向异性地层的水平电导率为σht=0.2 S/m,垂直电导率分别取σvt=0.02 S/m和σvt=0.05 S/m两种数值。保持侵入带水平电导率与垂直电导率的比值σh,xo/σv,xo=5不变,水平电导率σh,xo从0.001 S/m连续增加到20 S/m。图4给出了4组zz分量线圈系、两组xx分量线圈系的响应随侵入带水平电导率σh,xo的变化关系,由于zz分量的响应与地层垂直电导率σvt的取值无关,故图4(a)、图4(b)只给出了一种情况下的结果。

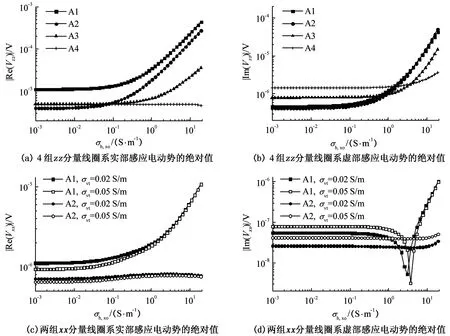
图4　侵入带电导率连续变化时的响应Fig.4　Responses with conductivity of invasion zone continuously varying

由图4(a)和图4(b)可知,当σh,xo较小时,4组zz分量线圈系实、虚部感应电动势的绝对值均变化缓慢,受井眼和地层电导率的影响相对较大,受σh,xo的影响相对较小。由图4(a),随着σh,xo的继续增大,前三组线圈距较短的线圈系实部感应电动势的绝对值均增加,而第四组线圈系的实部感应电动势仍无明显变化。而由图4(b),当σh,xo增大到某一数值后,第四组线圈系虚部感应电动势的绝对值亦随着σh,xo的继续增加而增加。由图4(c)和图4(d),当σh,xo处于数值较小的范围时,两组xx分量线圈系的感应电动势受井眼和各向异性地层电导率的影响相对较大,受侵入带电导率的影响相对较小,随σh,xo变化得较缓慢。由于在σh,xo较小时各向异性地层电导率的影响相对较大,地层垂直电导率σvt的不同导致同一组线圈系感应电动势数值也不同。由图4(c),随着σh,xo的继续增大,第一组短线圈距线圈系的实部响应快速增加,而第二组长线圈距线圈系的响应则在缓慢增加到极大值后缓慢减小。由于随着σh,xo的继续增大，侵入带电导率的影响逐渐增加,不同的σvt对应的同一组线圈系的实部感应电动势趋于一致。由图4(d),随着σh,xo的继续增大,第一组短线圈距线圈系的虚部感应电动势的绝对值快速减小,并在σh,xo增加到某一数值后(该数值针对不同σvt而不同)虚部感应电动势改变符号，并随σh,xo增加而快速增加,且由于侵入带电导率的影响逐渐增大,不同的σvt对应的虚部感应电动势趋于一致。第二组长线圈距线圈系的虚部感应电动势则没有出现符号改变情况,并且直到σh,xo增加到更大数值后其绝对值才有较明显的增加,并且也直到σh,xo增加到更大数值后不同的σvt对应的虚部感应电动势才趋于一致。

3.4多分量感应测井响应与地层各向异性系数的关系

忽略侵入带的存在,取井眼内钻井液电导率σm=1 S/m,保持均质各向异性地层水平电导率σht=0.1 S/m不变,水平电导率与垂直电导率的比值σht/σvt从0.1连续增加到100。图5给出了两组xx分量线圈系实部和虚部感应电动势的绝对值随σht/σvt的变化关系,由于zz分量感应电动势与地层各向异性系数无关,故未给出。

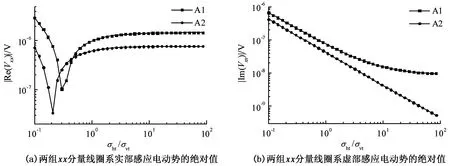
图5　地层各向异性系数连续变化时的响应Fig.5　Responses with anisotropic coefficients of formation continuously varying

由图5(a)可知,当σht/σvt较小时,随着σht/σvt的增加,两组xx分量线圈系实部感应电动势的绝对值快速减小(其感应电动势均为负值),当σht/σvt增加到某一数值后(该数值针对不同线圈距而不同),实部感应电动势变为正值，并随σht/σvt增加而增加,但增加速度越来越缓慢,最终趋于某一稳定值(该稳定值亦针对不同线圈距而不同)。由图5(b),两组xx分量线圈系虚部感应电动势的绝对值均随σht/σvt的增加而减小(其感应电动势均为负值),随着σht/σvt的继续增加,短线圈距线圈系虚部感应电动势的变化逐步趋缓并趋于某一稳定值,而长线圈距线圈系则需要σht/σvt增加到更大数值才趋于稳定。

4　结　论

(1) 利用由递推方法得到的柱状成层各向异性介质中并矢Green函数的解析式可高效模拟柱状成层各向异性地层中多分量感应测井仪器的响应。

(2) 共面线圈系的响应特性与共轴线圈系的响应特性完全不同。共面线圈系的响应特性更为复杂,对钻井液电导率、侵入带电导率、地层电导率、地层各向异性的变化更为敏感,且在很多情况下其响应会随这些参数的变化出现符号改变。

(3) 由于共面线圈系的同一响应可对应各向同性地层或各向异性地层的不同电导率,这给测量数据的解释处理带来了困难,须综合利用多种测量信息开发出更为先进的数据处理技术实现对多分量感应测井响应的精确解释。

参考文献:

[1]MORAN J H,GIANZERO S.Effects of formation anisotropy on resistivity-logging measurements [J].Geophysics,1979,44(7):1266-1286.

[2]KRIEGSHAUSER B,FANINI O,FORGANG S,et al.A new multi-component induction logging tool to resolve anisotropic formations [C/CD].SPWLA 41th Annual Logging Symposium,2000,paper D.

[3]MALLAN R K,TORRES-VERDIN C.Effects of petrophysical,environmental,and geometrical parameters on multi-component induction measurements acquired in high-angle wells [C/CD].SPWLA 47th Annual Logging Symposium,2006,paper PPP.

[4]WANG H N,SO P,YANG S W,et al.Numerical modeling of multicomponent induction well-logging tools in the cylindrically stratified anisotropic media [J].IEEE Trans Geosci Remote Sens,2008,46(4):1134-1147.

[5]GIANZERO S.Effect of sonde eccentricity on responses of conventional induction-logging tools [J].IEEE Trans on Geoscience Electronics,1978,16(4):332-339.

[6]LOVELL J R,CHEW W C.Response of a point source in multicylindrically layered medium [J].IEEE Trans Geosci Remote Sens,1987,25(6):850-858.

[7]LOVELL J R,CHEW W C.Effect of tool eccentricity on some electrical well-logging tools [J].IEEE Trans Geosci Remote Sens,1990,28(1):127-136.

[8]HAGIWARA T,BANNING E J,OSTERMEIER R M,et al.Effects of mandrel,borehole,and invasion for tilt-coil antennas [R].SPE 84254,2003.

[9]HUE Y K,TEIXEIRA F L.Analysis of tilted-coil eccentric borehole antennas in cylindrical multilayered formations for well-logging applications [J].IEEE Trans Antennas Propag,2006,54(4):1058-1064.

[10]魏宝君.一种新型随钻电阻率测井仪器的响应和刻度[J].地球物理学报,2007,50(2):632-641.

WEI Baojun.Response and calibration of a new logging-while-drilling resistivity tool [J].Chinese Journal of Geophysics,2007,50(2):632-641.

[11]汪宏年,陶宏根,姚敬金,等.用模式匹配算法研究层状各向异性倾斜地层中多分量感应测井响应[J].地球物理学报,2008,51(5):1591-1599.

WANG Hongnian,TAO Honggen,YAO Jingjin,et al.Study on the response of a multicomponent induction logging tool in deviated and layered anisotropic formations by using numerical mode matching method[J].Chinese Journal of Geophysics,2008,51(5):1591-1599.

[12]魏宝君,王甜甜,王颖.用磁流源并矢Green函数的递推矩阵方法计算层状各向异性地层中多分量感应测井响应[J].地球物理学报,2009,52(11):2920-2928.

WEI Baojun,WANG Tiantian,WANG Ying.Computing the response of multi-component induction logging in layered anisotropic formation by the recursive matrix method for magnetic-current-source dyadic Greens function [J].Chinese Journal of Geophysics,2009,52(11):2920-2928.

[13]俞燕明,肖加奇,魏宝君,等.用并矢Green函数的矢量本征函数展开式评价金属心轴对多分量感应测井响应的影响[J].中国石油大学学报(自然科学版),2014,38(4):57-64.

YU Yanming,XIAO Jiaqi,WEI Baojun,et al.Evaluating influence of metal mandrel on response of multi-component induction logging by vector eigenfunction expansion formulae for dyadic Greens functions[J].Journal of China University of Petroleum (Edition of Natural Science),2014,38(4):57-64.

[14]魏宝君,王成园,俞燕明,等.用并矢Green函数的矢量本征函数展开式模拟多分量感应测井仪器的刻度[J].中国石油大学学报(自然科学版),2015,39(2):39-47.

WEI Baojun,WANG Chengyuan,YU Yanming,et al.Simulating multi-component induction logging tools calibration by vector eigenfunction expansion formulae for dyadic Greens functions[J].Journal of China University of Petroleum (Edition of Natural Science),2015,39(2):39-47.

[15]CHEW W C.Waves and fields in inhomogeneous media [M].New York:Van Nostrand Reinhold,1990.

[16]戴振铎,鲁述.电磁理论中的并矢格林函数[M].武汉:武汉大学出版社,1996.

(编辑修荣荣)

Simulating responses of multi-component induction logging tools by dyadic Greens functions in cylindrically stratified anisotropic media

WEI Baojun1,2,WANG Chengyuan1,DANG Feng3,CHANG Xinli1,CAO Jingqiang1

(1.College of Science in China University of Petroleum,Qingdao 266580,China;2.Key Laboratory of New Energy Physics & Material Science in Universities of Shandong,China University of Petroleum, Qingdao 266580,China;3.China Petroleum Logging Company Limited,Xian 710077,China)

An analytical expression of dyadic Greens functions in cylindrically stratified anisotropic media (transversely isotropic media) was obtained using a recursive method.The expression can be used to simulate the response of an arbitrary point source (including electric source and magnetic source) in cylindrically stratified anisotropic formations.The expression can be applied to any number of formation layers,and with the source location and field location in any of the layers.Using the method,the responses of multi-component induction logging tools with a metal mandrel and an insulating protection layer were simulated in anisotropic formations with a borehole and an invasion zone.The shape of each components coils was taken into account in order to increase the simulating precision,and the metal mandrel was taken as a layer whose conductivity can be both finite and infinite.The simulation results show that the response of coplanar coil system has entirely different characteristics from that of coaxial coil system:the response of coplanar coil system is often more complex and more sensitive to the change in drilling liquid conductivity,invasion zones conductivity,formation conductivity,and formation anisotropy.These parameters may even cause sign flip in the response under many conditions.Furthermore,since the same response of coplanar coil system may be produced by entirely different formation conductivities in isotropic or anisotropic formations,it will become much complicated to interpret or process the measured data.

multi-component induction logging； dyadic Greens functions； cylindrically stratified anisotropic media； metal mandrel； invasion zone

2015-05-20

国家科技重大专项(2016ZX05019007);中央高校基本科研业务费专项资金(15CX05047A);中国石油天然气集团公司科学研究与技术开发项目(2014D-4018)

魏宝君(1969-)，男，教授，博士，教育部“新世纪优秀人才支持计划”入选者，研究方向为电磁测井理论及应用。E-mail:weibj@upc.edu.cn。

1673-5005(2016)02-0059-11doi:10.3969/j.issn.1673-5005.2016.02.007

P 631.9

A