时滞环境下广义马尔可夫跳变系统的H∞滤波

颜秋林 苏晓杰 龚骏

过去的几十年中,对动态系统滤波问题进行了广泛的研究.不同于传统的卡尔曼滤波,对于输入中包含未知干扰噪声的系统,H∞滤波应用广泛,例如在文献[1−6]中.一方面,马尔可夫跳变系统已经成功地被用来模拟遇到突发环境干扰、器件故障或修复以及实际操作中突然发生变化的系统.与此相关的研究成果能够在相关文献中查阅.文献[7]中主要探讨二阶马尔可夫跳变系统的广义H2故障检测;输出反馈控制马尔可夫跳变重复标量非线性系统的输出反馈控制在文献[8]中被关注.文献[9]研究了带有时滞的马尔可夫跳变系统的滤波.另一方面,广义系统相较于常规系统能更好地描述物理系统动态特性,因而它在电子电路、电力系统、经济和其他领域中有着广泛的应用,过去的几十年中对广义系统已经引起相当的关注[10−11].此外模糊广义系统的非脆弱保成本控制问题在文献[2]被研究,更多关于广义系统的研究成果请参考文献.此外一些基本但重要的广义马尔可夫跳变系统成果被提出来在文献[13−16].然而很少有结果旨在解决带有时滞的广义离散马尔可夫跳变系统.

本文目标是考虑带有时滞的广义离散马尔可夫跳变系统的H∞滤波问题.目的是设计一个滤波器以致滤波误差系统是带有H∞性能指标的随机可容许.首先用严格的线性矩阵不等式提出此问题的可解性条件,然后基于此条件,当转移矩阵率全部已知的情况下,时滞依赖结果被提出.最后通过一个数值例子来证明此方法的有效性.

1 问题描述

考虑如下这类离散广义常时滞马尔可夫跳变系统:

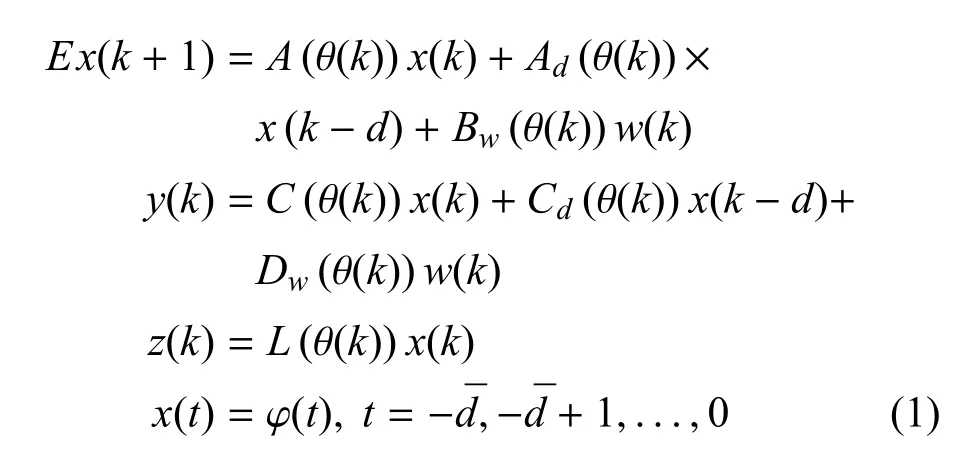
其中,x(k)∈Rn是状态,y(k)∈Rs是测量输出信号,z(k)∈Rq是被估计的信号,w(k)∈Rp是扰动输入并且满足是未知的但满足0≤的正整数常时滞,φ(k)是状态的初始值函数,{θ(k),k∈Z+}是一个离散的马尔可夫链,它的取值是一个有限状态集合S={1,2,...,N},首先假定系统整个转移概率矩阵都是已知的,并用Π=[πij]i,j∈S来表示,πij=pr(θ(k+1)=j|θ(k)=i)≥ 0,∀i,j∈S,k∈Z+,表示从k时刻所处模态i转移至k+1时刻所处模态j的概率,另外对任何i∈S的情况还满足特性,矩阵E的秩是满足rank(E)=r≤n的广义矩阵,为书写方便,矩阵A(θ(k)),Ad(θ(k)),Bw(θ(k)),C(θ(k)),Cd(θ(k)),Dw(θ(k)) 和L(θ(k)) 用A(k),Ad(k),Bw(k),C(k),Cd(k),Dw(k)和L(k)来表示,此外它们是已知的并具有合适维度的系统矩阵.

论文目的是为系统式(1)设计线性滤波器,其形式如下:

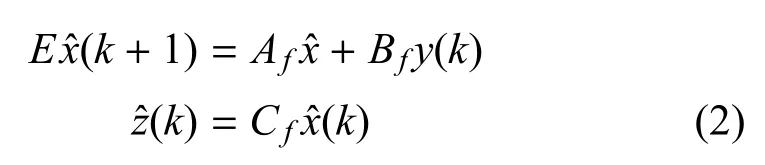
首先做如下定义:

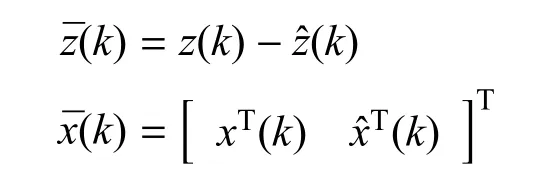
根据定义可容易得到如下滤波误差系统:

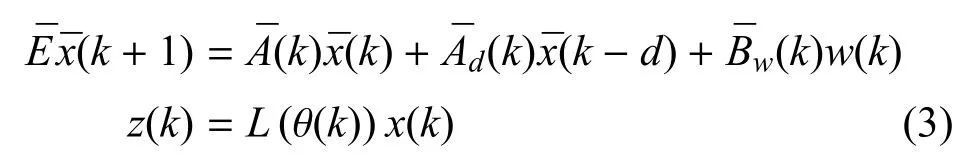
其中:

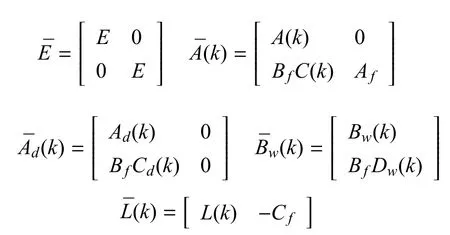
在此先引入论文后续会用的定义和概念.

定义1.给定标量>0,对于离散广义常时滞马尔可夫跳变系统如下所示:

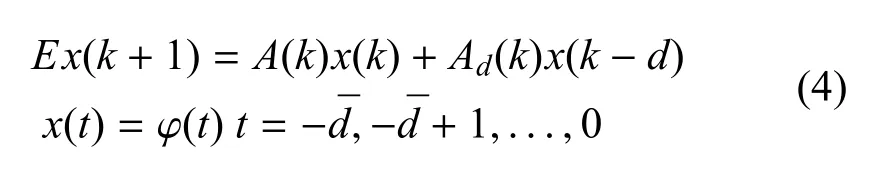
①如果矩阵对(E,A(k)),(E,A(k)+Ad(k))对任意θ(k)∈S的情况,它们都是正则性和因果性的,那么系统式(4)在任何常时滞d满足于0≤d≤d的条件下,都是正则性和因果性的;

②如果存在一个标量 Γ(θ(0),ϕ(·))以致满足

③如果系统在任何θ(k)∈S的前提下,它既是正则性、因果性,同时又是随机稳定的,那么离散广义常时滞马尔可夫跳变系统式(4)是随机可容许.

定义2.给定一个标量γ>0,对于离散广义常时滞马尔可夫跳变系统,如果系统在w(k)≡0的情况下是随机可容许,并且在零初始条件下对于任何非零的情况下都满足那么系统是具有H∞性能γ随机可容许.

文章要处理的H∞滤波问题简单表述为:对于给定一个标量γ>0和离散广义时滞马尔可夫跳变系统式(1),设计一个如式(2)的线性滤波器以致使滤波误差系统式(3)是带有H∞性能γ随机可容许.

为书写简单,后续的推导过程中,对于每一个可能的θ(k)=i,i∈S的取值,矩阵A(θ(k))用Ai来表示,其他情况参照.

引理1.对标量d>0和任意对称正定矩阵M∈Rn×n,下面不等式总是成立的.

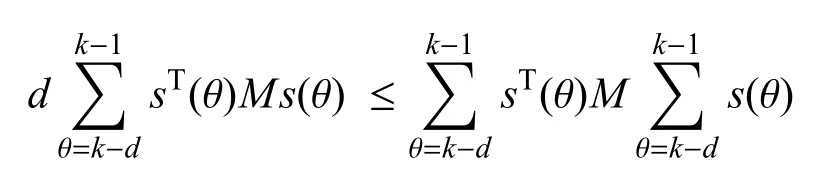
相关文献中给出了离散广义马尔可夫跳变系统随机可容许的充要条件,它的系统模型如下:

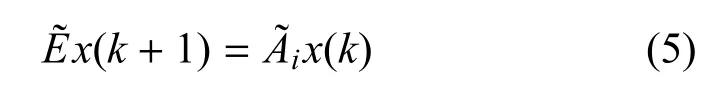
引理2.如果存在对称正定矩阵Pi和矩阵Si满足下式

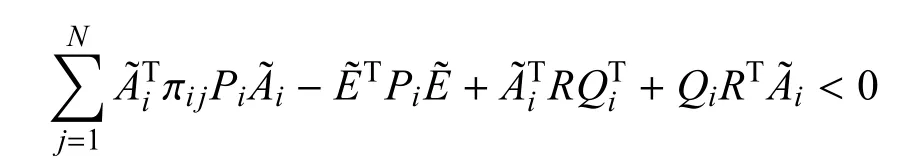
其中R∈Rn×(n−r)是任意列满秩矩阵并满足ETR=0,那么系统式(5)是随机可容许.

2 主要结果

在这一节中,离散广义常时滞马尔可夫跳变系统H∞滤波问题将通过LMI工具来进行研究,首先为系统提出下面时滞有界实引理,它在后面主要结果推导中将会扮演重要角色.

下面给出关于系统带有H∞性能指标γ随机可容许的线性矩阵不等式形式的充分条件.为表达方便,先给出一些必要说明:和

定理1.给定标量>0和γ>0,如果存在对称正定矩阵Pi>0,Q1i>0,Z>0,M>0和矩阵Qi,在任意i∈S的情况下,都满足线性矩阵不等式(6)和式(7),那么对于离散广义常时滞马尔可夫跳变系统式(1)在任何常时滞d满足0≤d≤的情况下是带有H∞性能指标 γ随机容许的.此外R∈ R(n−r)×(n−r)是任意列满秩矩阵并且满足ETR=0.

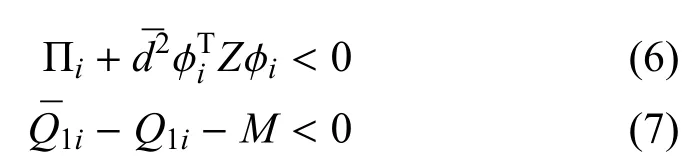
其中:

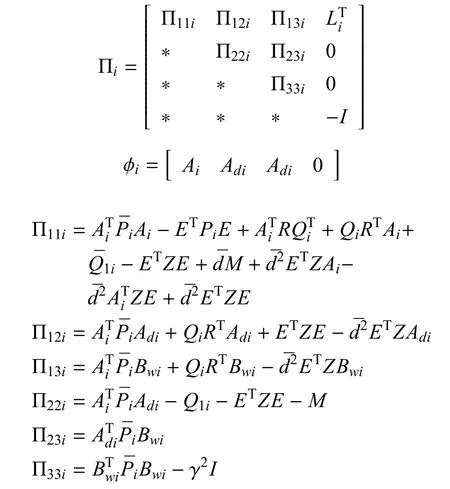
证明.首先根据定义1,第1步要证明离散广义时滞马尔可夫跳变系统的正则性和因果性.因为rank(E)=r≤n,所以这里必然存在非奇异矩阵M和N满足下面的式子:

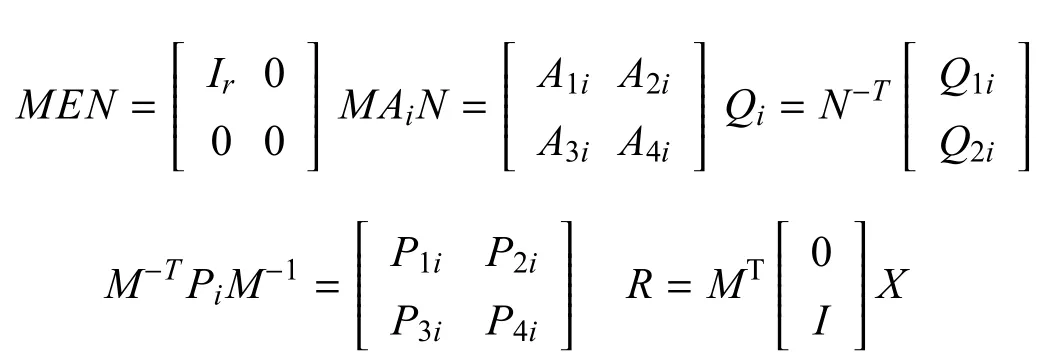
其中X∈ R(n−r)×(n−r)是任意非奇异矩阵,对 Π11i<0分别前乘NT和后乘N,可得意味着A4i在i∈S情况下都是非奇异的,故矩阵对(E,Ai)是正则性和因果性的,根据Shcur补引理从可以得到由此得Π11i+Π12i+ΠT12i+Π22i<0,从而能够得到式子:

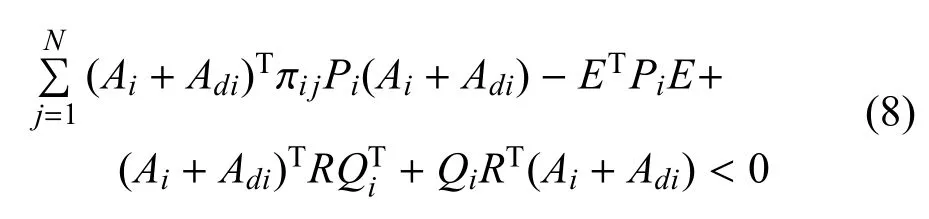
根据引理2,式(8)证明了矩阵对(E,Ai+Adi)对任意i∈S是正则性和因果性的.从而根据定义1,系统在任意常时延d并满足于0≤d≤情况下都是正则性和因果性的.

接着证明系统随机稳定性,证明前,先给出必要的定义,s(k)=x(k+1)−x(k),现在为系统式(1)选取如下随机李雅普诺夫函数:

其中:

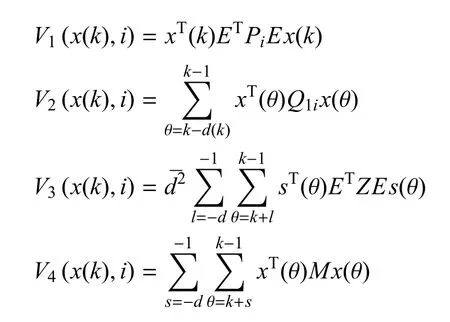
对李雅普诺夫函数V(x(k),i)取差分,可以得到如下结果:

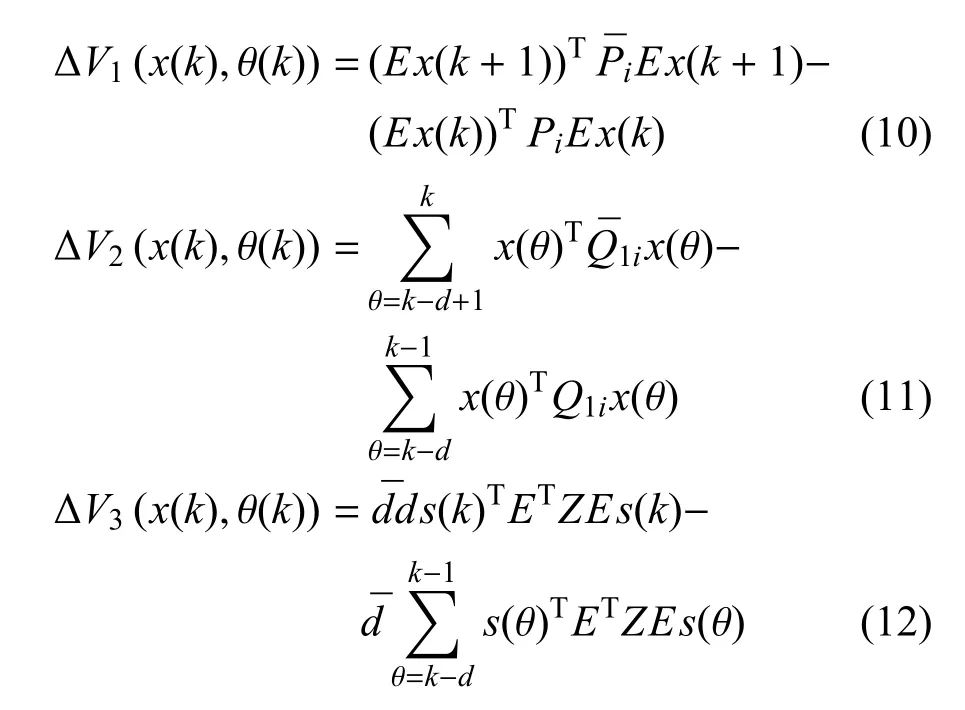
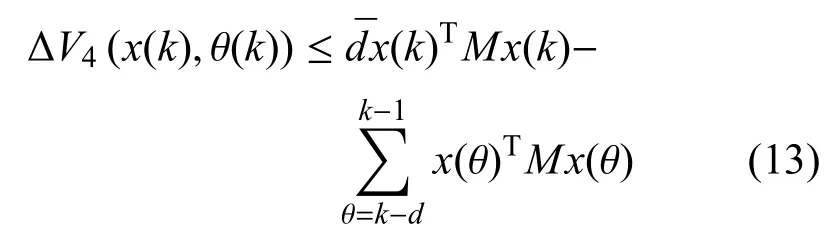
通过引理1,可以得到

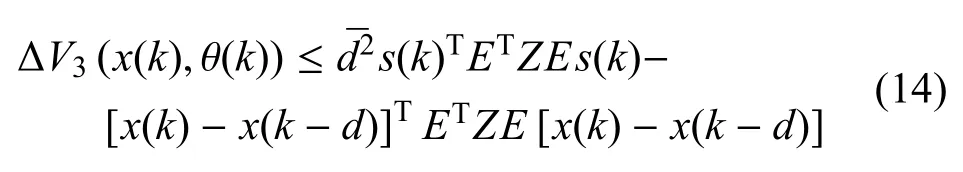
注意:

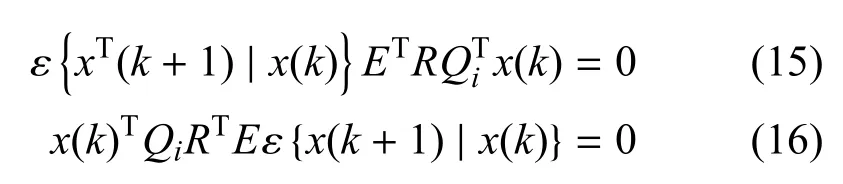
然后从式(10)∼式(16)可以得到

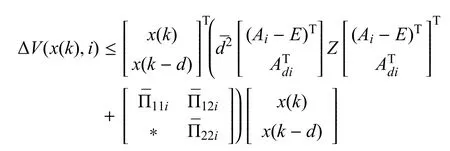
其中:

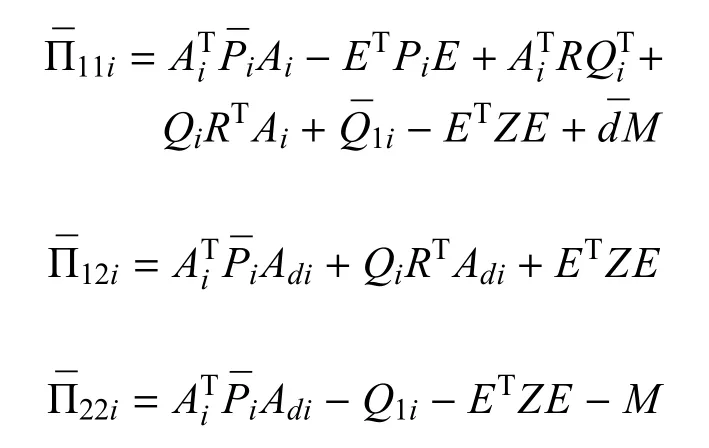
利用线性矩阵不等式(6)和式(7),能够容易得到∆V(x(k),i)≤0,因此,存在一个标量γ>0对任意i∈S都有∆V(x(k),θ(k))≤γkx(k)k2,因而通过Dynkin公式,能得到对于任何k≥0都有ε{V(x(k),i)}−进而通过对其变形可以容易地得到下式考虑定义 1,系统式 (1)在w(k) ≡ 0的情况下对任意常时滞d满足于0≤d≤都是随机稳定的.

接下来将为系统式(1)建立起H∞性能指标γ,为了完成这一目的,再次思考上面所选的随机李雅普诺夫函数式(9)以及如下性能指标

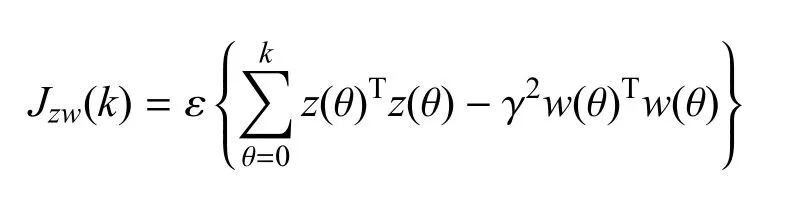
在零初始条件下,可以容易得到

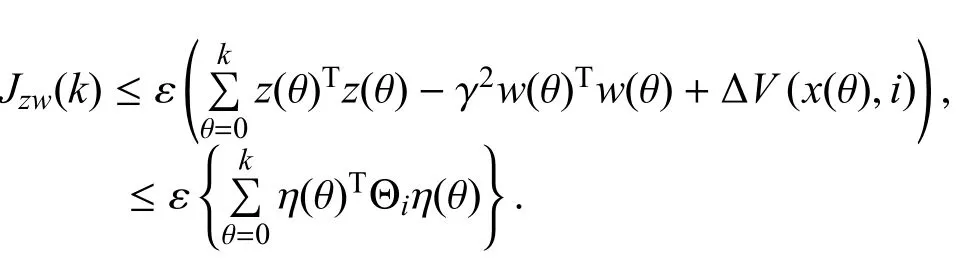
其中:

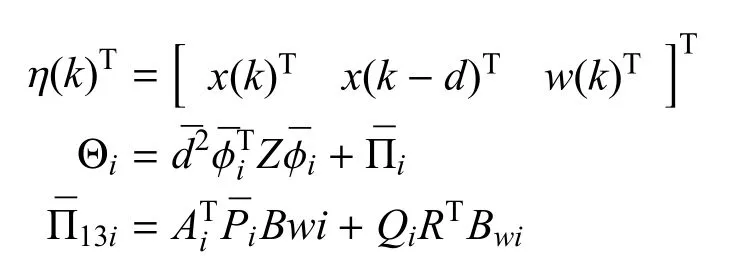
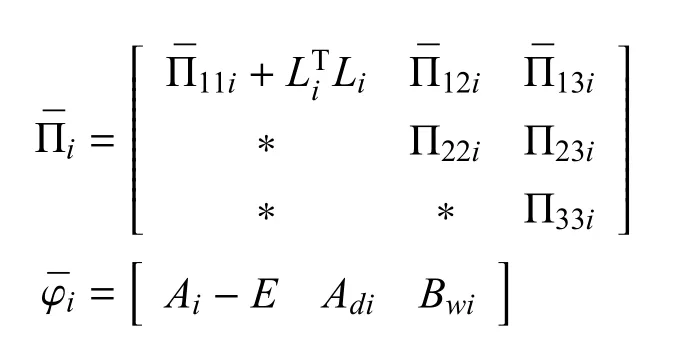
因此,通过Schur补引理,从式(6)和式(7)可以得到对所有的k≥0,Jzw(k)≤0是成立的.因此,证明完成.

到现在为止已经处理离散广义常时滞马尔可夫跳变系统H∞滤波问题,接下来应用定理1到滤波误差系统中,可以得到如果存在对称正定矩阵Pi,Q1i,Z,M和矩阵Qi对任意i∈S都满足线性矩阵不等式(17)和式(18),那么滤波误差系统对于任意满足0≤d≤的常时滞d都是带有H∞性能指标γ的随机可容许.另外任意列满秩矩阵R∈R2n×2(n−r)并满足R=0.

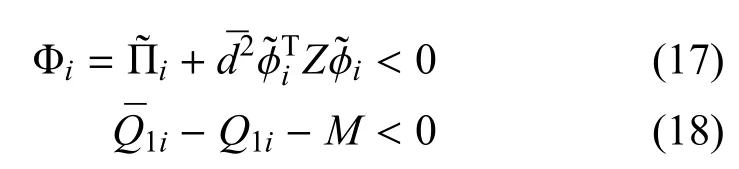
其中:

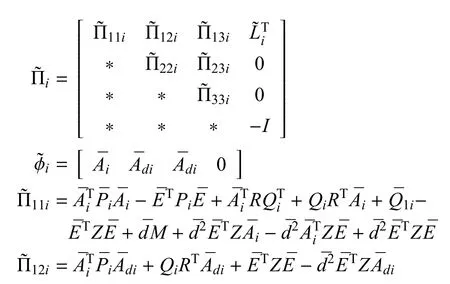
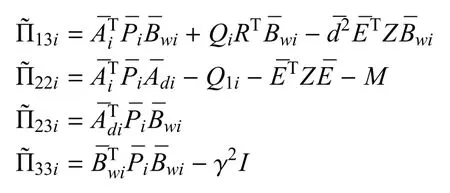
很容易地可以发现对于任意i∈S

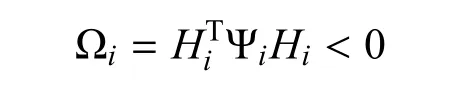
其中:

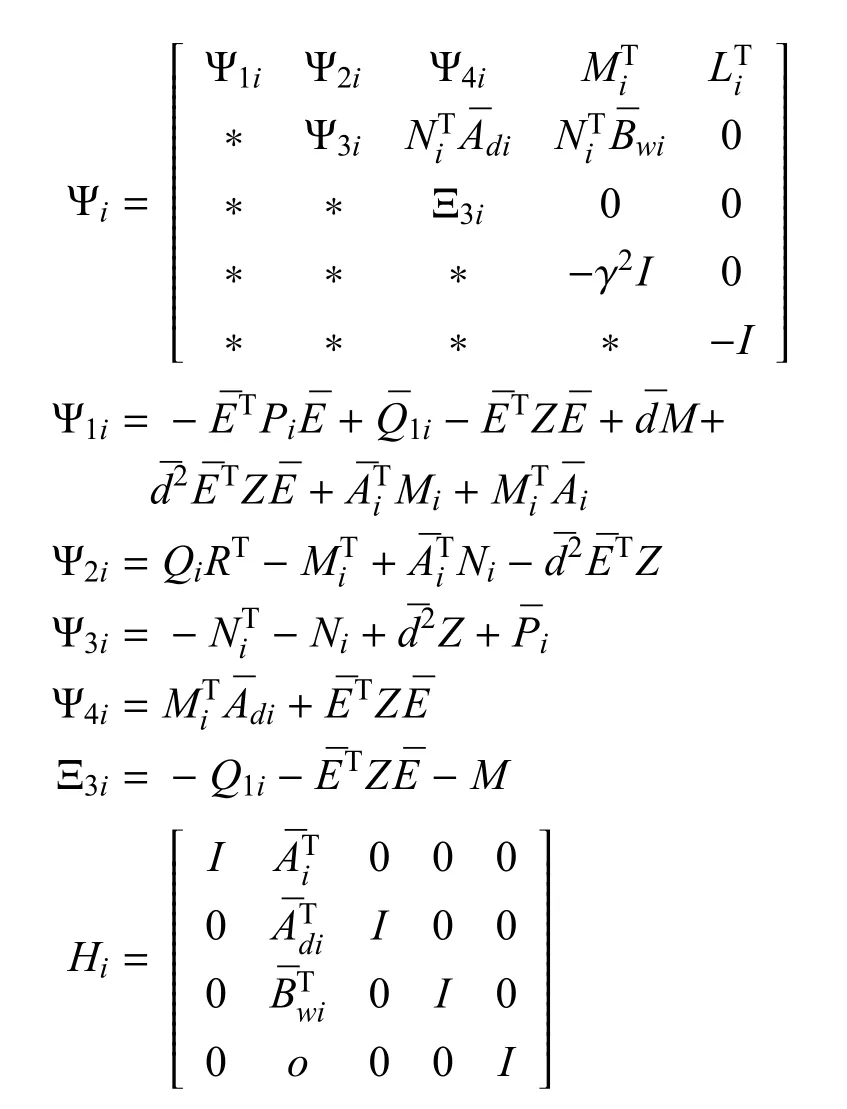
式中,Ωi<0意味着Ψi<0.取Ψi和线性矩阵不等式(18)中的矩阵如下:

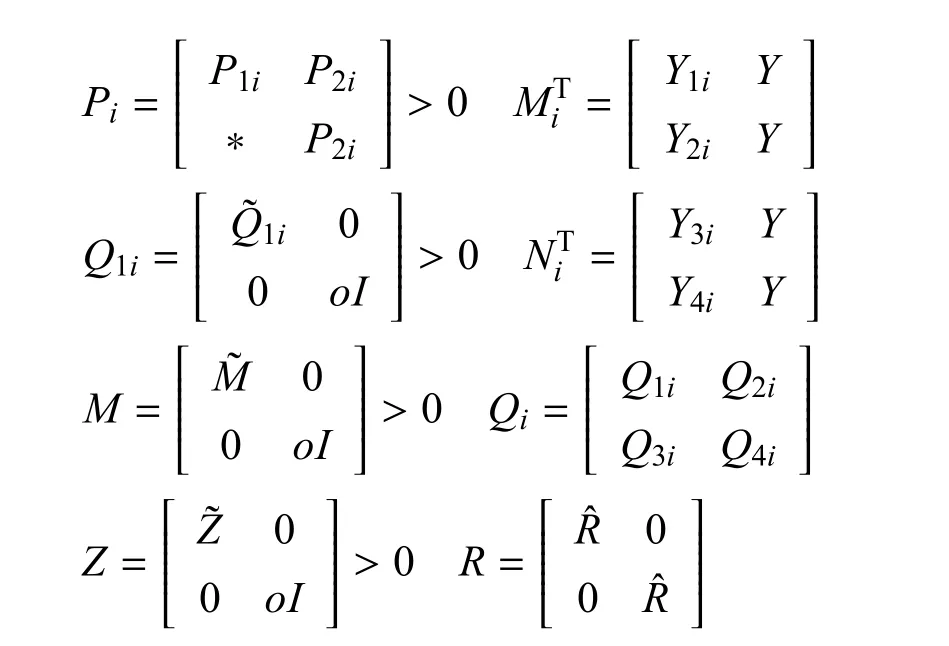
现在,假定o→0,同时定义A=YAf,B=YBf和C=Cf.进而可以很容易地得到系统时滞依赖的带有H∞性能指标γ随机可容许条件.

定理2.对于给定标量和γ,如果存在对称正定矩阵和矩阵Q1i,Q2i,Q3i,Q4i,Y1i,Y2i,对于任何i∈S都满足线性矩阵不等式(19)和式(20),那么离散广义常时滞马尔可夫跳变系统式(3)在满足0≤d≤d的任意常时滞情况下都是带有H∞性能指标γ随机可容许.另外任意列满秩矩阵并满足

此时所期望的滤波器参数为:

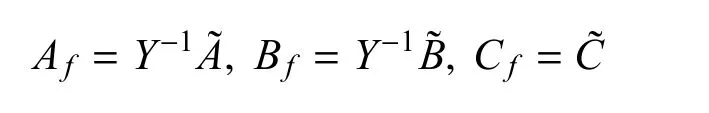
到此为止,期望的线性滤波器理论推导已经完成,下面通过数值例子来仿真,进一步验证所得到结论的正确性.

3 仿真结果

在这部分中,通过选取一个数据例子用来验证上一小节中所提出的结论.现在考虑带有两个模态的离散广义常时滞马尔可夫跳变系统,即S={1,2},系统矩阵参数可以描述为如下:

模态之间转移概率矩阵π和系统广义矩阵E分别取值为

应用定理2,能够获得期望滤波器参数为:

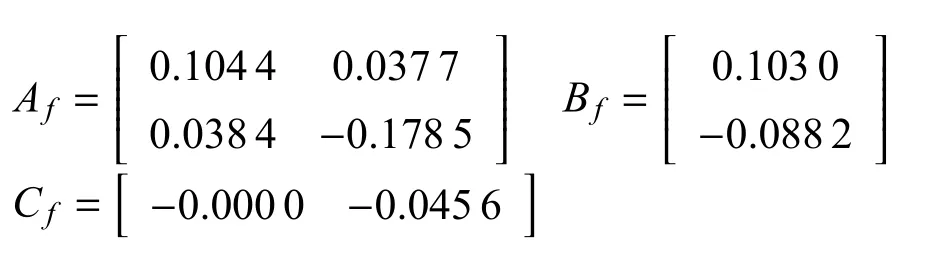
关于期望滤波器为一种可能的马尔可夫跳变模态在图1中所示,其中初始模态假设为θ(0)=1和时滞d=1.图2是扰动输入为w(k)=sin(k)e−0.1k以及初始状态为的情况下所期望的滤波器状态曲线,误差估计信号在图3中所示.

4 结论

论文主要研究离散广义常时滞马尔可夫跳变系统H∞滤波问题,使用线性矩阵不等式方法,所得条件用严格线性矩阵不等式组形式表达,这样便于利用标准工具软件进行求解,所期望的线性滤波器的求解条件是时滞依赖的.最后通过选取一个数值例子进行仿真,进一步验证所得结果的正确性.

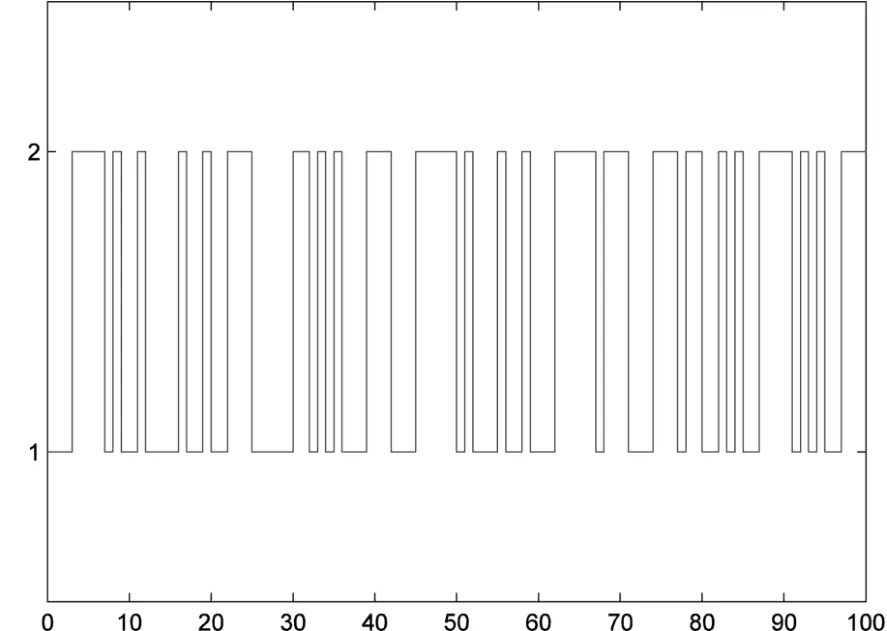
图1 系统模态

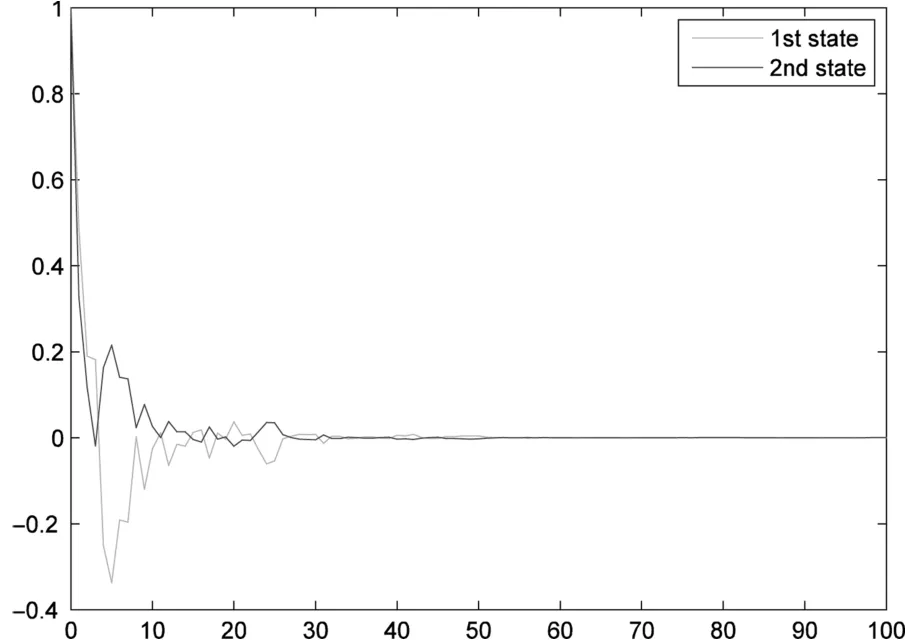
图2 滤波器状态

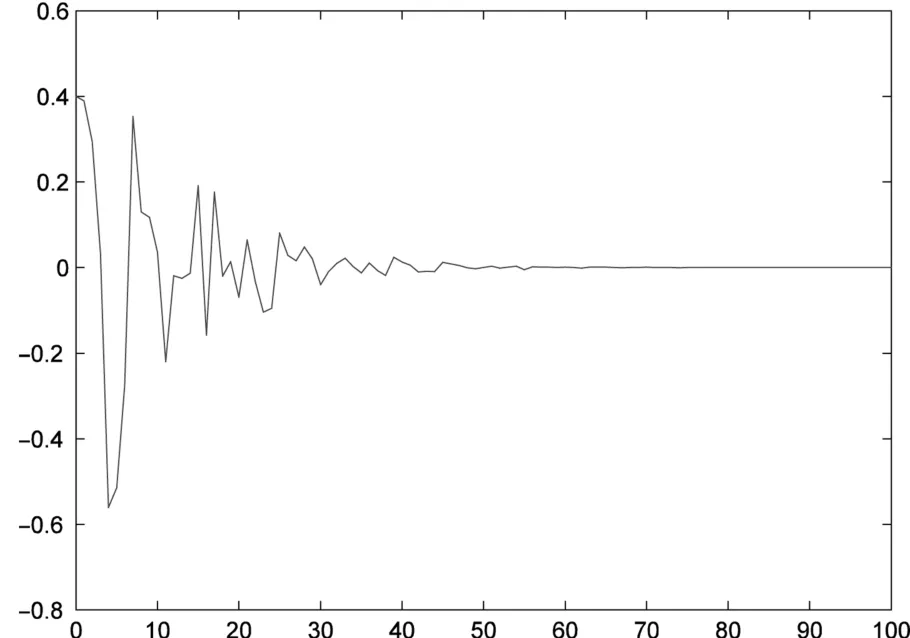
图3 估计误差