与单目标打击方案和发射地域相关的快速大规模火力任务分配
黄红兵 李贤玉 张连伟 邹辉
火力任务分配是作战任务规划的一项重要内容.因面临的问题不同,实际作战任务规划中的火力任务分配问题有很大的差别(如诸多工作所展示的[1−7]).实际工作中存在这样一类问题:给定一大批打击目标,每个目标都有若干单目标打击方案,每个单目标打击方案涉及的武器可能分属不同作战单位,而每个作战单位只能在有限的几个作战区域进行发射活动;在此前提下,需要在给定的武器、兵力、发射地域等诸多约束条件下,针对若干优化目标,给出单目标打击方案选择及发射地域分配.特别是在指挥决策层次上,需要考虑错综复杂的约束关系和决策因素,大大加大了这类大规模火力任务分配的难度.
针对这一类问题,本文将诸多决策因素作为约束条件或优化目标引入问题,给出了详细的问题模型,设计了问题求解的遗传算法,并通过实验验证了大规模火力分配算法的快速性.
1 问题描述
设需要打击的目标有n个,分别为T1、T2、···、Tn;对每个目标Ti有ui个不同的单目标打击方案Pi1、Pi2、···、Piui;每个单目标打击方案包括使用的武器类型和需要的数量,如表1所示.
设共有m个可用发射地域Z1、Z2、···、Zm,分属o个作战单位Dw1、Dw2、···、Dwo,发射地域与作战单位对应关系矩阵如表2所示,其中dij为0或1,表示发射地域Zj不属于或属于作战单位Dwj;对于发射地域Zi有vi个可用阵地ZDi1、ZDi2、···、ZDivi称vi为该发射地域的容量.
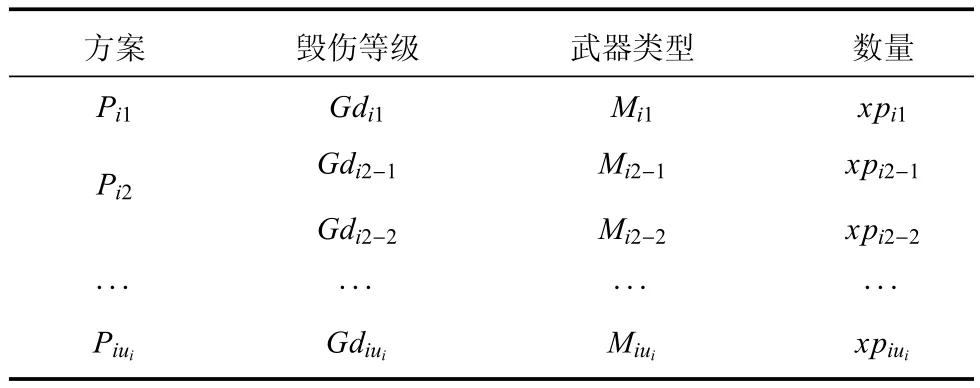
表1 单目标打击方案
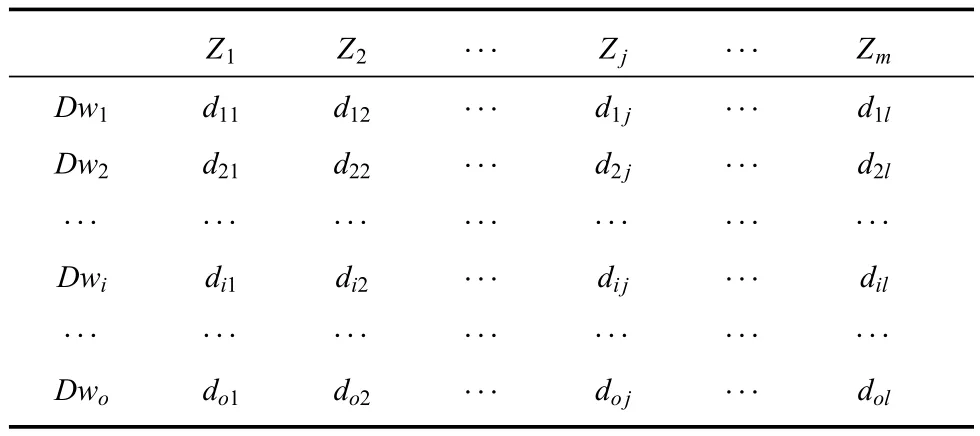
表2 发射地域与作战单位对应关系矩阵
设共有l种武器M1、M2、···、Ml,数量分别为xd1、xd2、···、xdl;对于作战单位Dwi,设其各类武器的保有量为xdi1、xdi2、···、xdil.
整个火力任务分配问题就是,按照给定的约束条件和优化目标(具体见第2节),为每个打击目标选择单目标打击方案,并分配到具体的发射地域,如表3所示.其中,biuij为0或1,1表示对于Ti方案Piui被选中,并且分配到发射地域Zj.只要给出这一分配矩阵,就可以通过相关条件,统计得到各作战单位的任务分配,因而表3中的biuij可以作为火力分配规划问题的决策变量.
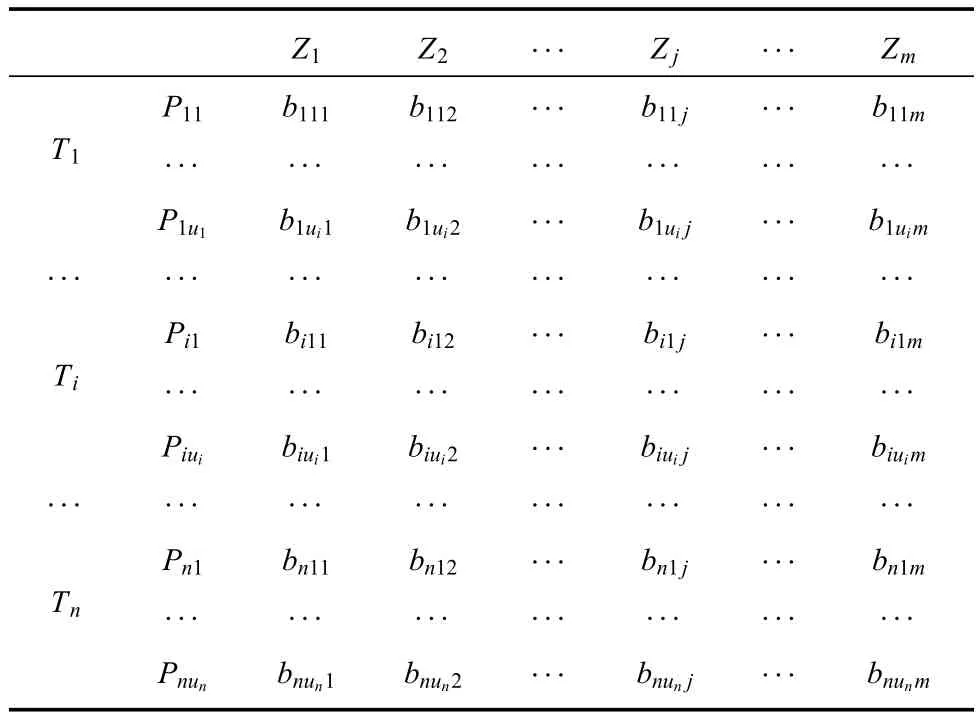
表3 火力任务分配及其决策变量
2 数学模型
针对以上问题,将复杂的相关关系和决策因素作为约束条件或优化目标引入问题,建立数学模型.
2.1 约束条件
根据问题和实际情况,这些约束如下.
1)单目标打击方案被选唯一性及发射区域分配唯一性约束
这一约束下,对于每个目标Ti,表3中对应的火力任务分配决策变量biuij只有一个取1,即:
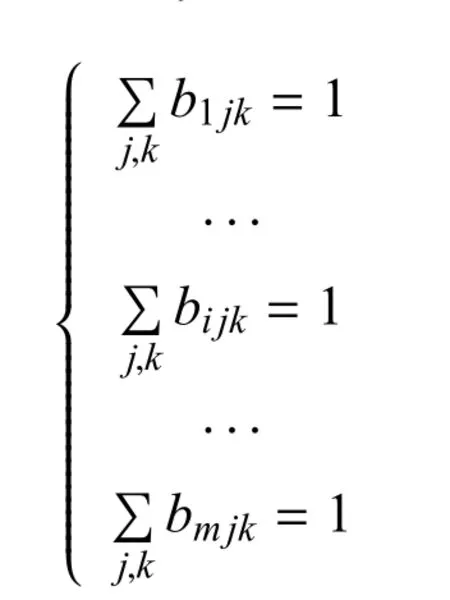
2)武器数量总量约束
指的是根据实际武器保有量或指挥员决策要求,对分配规划中武器类型使用的总量进行约束.
以矩阵的形式表示确定毁伤等级的单目标打击方案的武器使用,如表4所示.
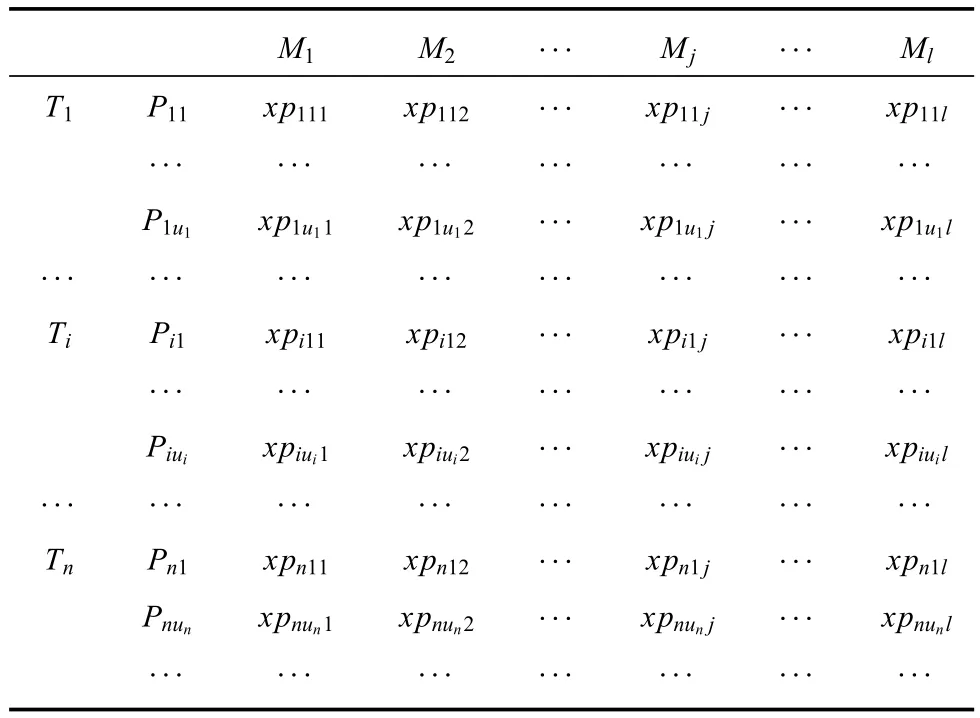
表4 单目标打击方案武器使用数量矩阵
那么,这一约束可以表示为:
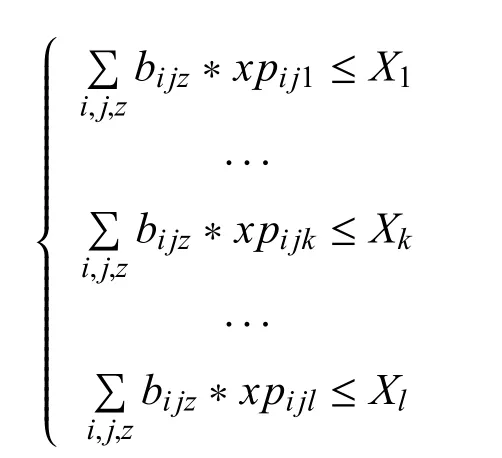
3)作战单位武器数量约束
指的是根据实际各作战单位保有的武器数量或指挥员决策要求,对分配规划中各作战单位武器使用的数量进行约束.
以矩阵的形式表示各作战单位拥有或允许使用的武器数量,如表5所示.
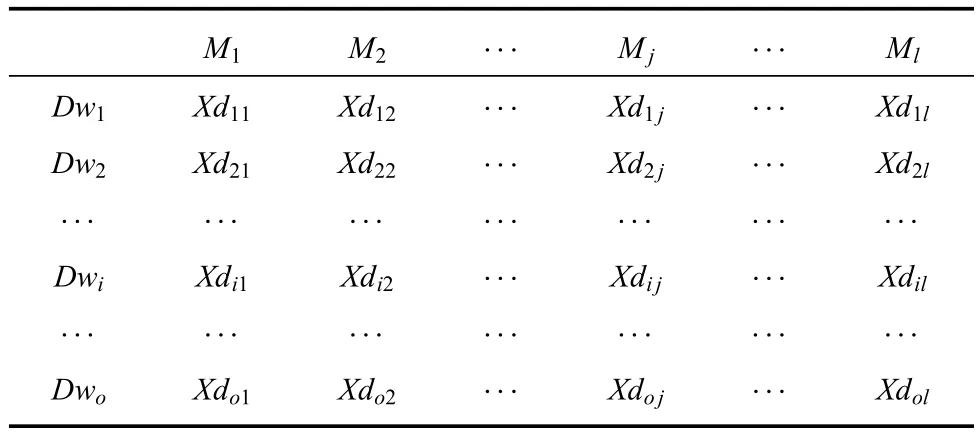
表5 各作战单位拥有或允许使用的武器数量矩阵
那么,这一约束可以表示为:
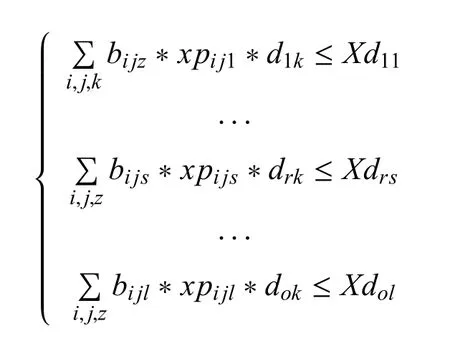
4)武器射程约束
设武器Mk的射程为Sck,发射地域Zj与目标Ti之间的距离为Lij.如果火力分配决策矩阵中(表3)的biuij为1,并且假设单目标打击方案武器使用数量矩阵中(表4),方案Piui对应的数量不为0的武器为Mk,那么,武器射程约束可表示为:
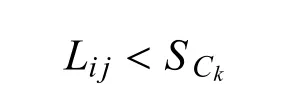
5)发射地域容量约束
实际作战中,每个发射地域安排发射的武器数量小于等于发射地域的容量v.结合表3、表4,这一约束可以表示为:
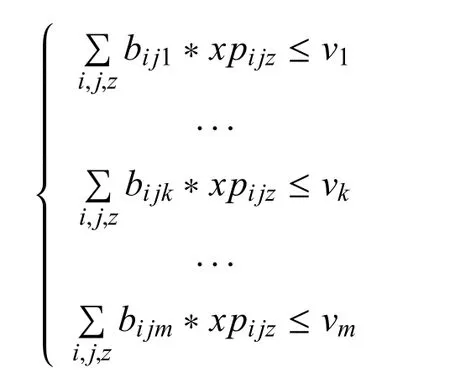
6)作战单位作战单元数量约束
实际作战中,每个作战单位发射的弹量,应小于作战单位作战单元数量乘以发射波次.设波次数为c,每个作战单位Dwi的作战单元数为Gi,结合表2、表3和表4,这一约束可以表示为:
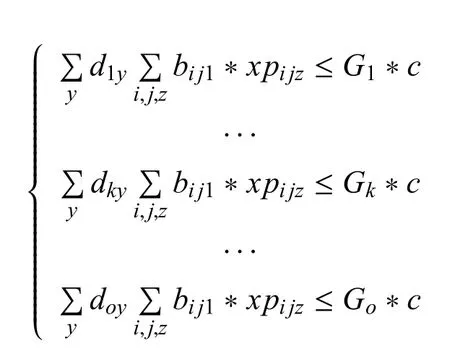
2.2 优化目标
根据实际情况和指挥员的意图,这类问题的大规模火力任务分配可能有多个目标.
1)最小弹量
在满足相关约束的条件下,使用的弹量最少.将决策变量集{biuij}记为B,则目标函数可以表示为
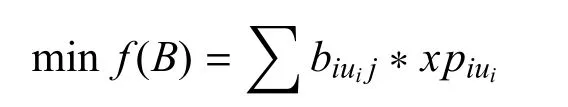
2)最少(或最多)建制单位
在满足相关约束的条件下,使用的建制单位最少(或最多).将表3中火力分配(决策变量)矩阵的行向量记为Bi,将表2中发射地域与作战单位对应关系矩阵记为Rz,则最少(或最多)建制单位目标函数可以表示为
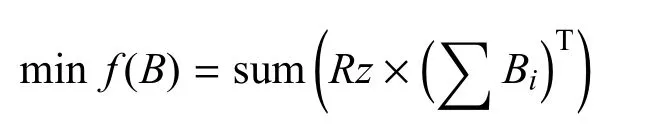
或
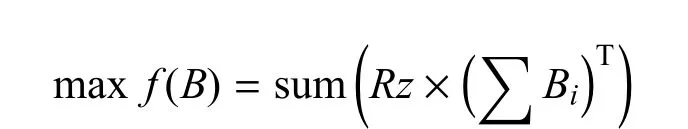
3)弹道平面交叉最少
假设目标Ti与发射地域Zj的平面弹道为Sij,弹道之间的交叉关系用如表6所示的矩阵表示,其中表示Sij和Sxy是否交叉(值的计算可以按照诸如文献[8]的给出方法进行).
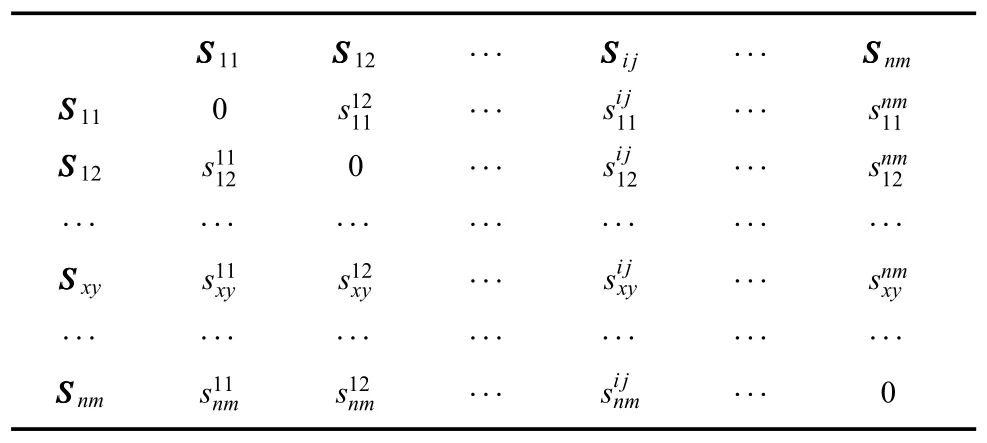
表6 弹道之间的交叉关系矩阵
则弹道平面交叉最少的优化目标函数可以表示为
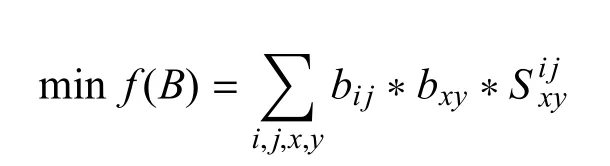
4)值班发射地域优先使用
假设有值班发射地域Zi1、Zi2、···、Zir,则值班发射地域优先使用的优化目标函数可以表达为
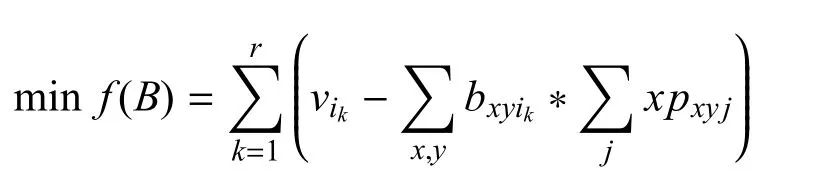
5)值班武器优先使用
假设作战单位Dwi的值班武器Mj的数量为Zdij.将表4中火力分配(决策变量)矩阵记为B,将表2中发射地域与作战单位对应关系矩阵记为Rz,将表4中单目标打击方案武器使用数量矩阵记为X,列向量记为Xj,定义函数
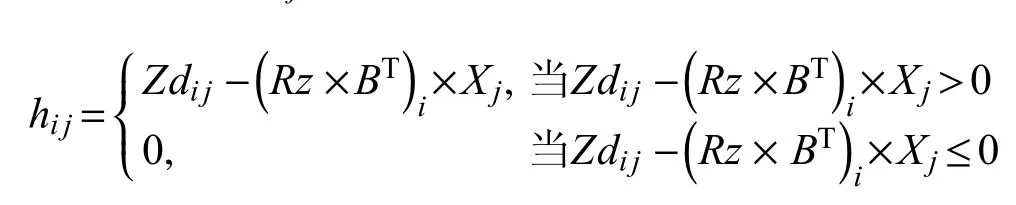
则值班武器优先使用的优化目标函数可以表达为
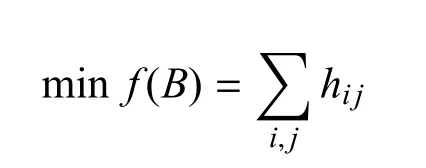
3 分配算法
从算法设计理论上看,任务分配最优化是NP难问题,实际工作中一般是通过近似算法,给出次优解.本节根据上述火力任务分配多目标优化模型和相关研究[9−10],给出火力任务快速分配的遗传算法.
3.1 算法描述
火力任务快速分配遗传算法的总体过程如图1所示.

图1 火力任务快速分配遗传算法的总体过程
具体问题处理如下:
1)个体编码
火力任务快速分配遗传算法中的每个个体,都设计成一个任务分配方案,即表3所示的矩阵,在这个矩阵中包括了单目标打击方案的选取和目标打击发射地域的分配.因此,对个体适应度的计算也就是对一个任务分配方案的评价(适应度的计算,具体见后文).
2)初始化种群
考虑到个体编码中的每个基因也是一个决策变量,为保证种群的多样性,初始化种群时,种群规模选取为.

并且,种群个体产生时遵守“单目标被选打击方案唯一性及发射地域分配唯一性约束”,以保证每个个体的有效性.
3)交叉变异规则
在种群交叉过程中,父亲个体的选取根据个体的适应度进行,适应度大的个体被选取的概率大,同时为避免种群收敛过快,保证每个个体都有可能被选取,每个个体选为父亲的概率为
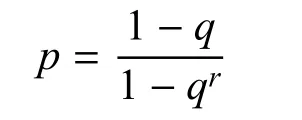
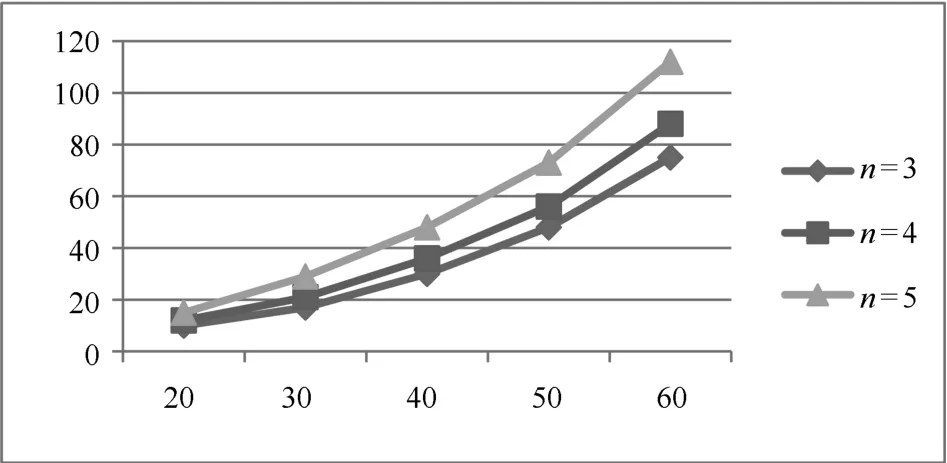
其中,0 在种群交叉过程中母亲个体的选取,则随机进行,每个个体的选取概率为 种群个体变异过程设计成两种:a)发射地域分配方案变异;b)单目标打击方案选择变异.发射地域分配方案变异,只是改变分配方案(个体)中被选择打击目标的发射地域;单目标打击方案选择变异,则对被选变异目标的单目标打击方案选取和发射地域分配,都作出改变. 和初始化种群一样,为保证每个个体的有效性,在种群交叉变异过程中,遵守“单目标被选打击方案唯一性及发射地域分配唯一性约束”.也就是说,在交叉过程中,父亲个体和母亲个体交换的是关于某个打击目标的整个方案,包括其单目标打击方案选取和发射地域分配;变异也是针对某个目标的单目标选取和发射区域分配的整个方案. 4)适应度计算 算法设计中,将个体适应度分为两个大的部分:a)对约束条件的适应度;b)对优化目标的适应度. 由于火力任务分配首先要满足约束条件,所以,对于有不满足约束条件的分配方案(即个体),计算时赋予它极小的适应度. 优化目标适应度的计算按照2.1给出的目标函数进行.对多个优化目标的满足可以采取两种策略:a)为优化目标排序,按顺序满足,即在上一目标优化的前提下,优化下一目标;b)为优化目标赋予权值,化作单目标进行优化. 5)代际更新与算法终止规则 种群交叉和个体变异后产生新一代的种群,为保证算法能够终止,给更新代数设定一个最大值. 同时,为保证算法效率,当种群适应度达到一定的要求时,终止算法.这一要求为 其中,δ为一个极小值. 以Matlab实现算法,在表7所示的运行环境下,进行算法效率的实验,结果如图2. 表7 实验运行环境 实验主要参数:发射地域数目为20,每个目标的单目标打击方案平均个数分别为n=3、4、5,目标个数分别为20、30、40、50、60. 实验所得数据:如图2,其中纵轴数据单位为“秒(s)”. 图2 火力任务快速分配算法效率 本文针对这样的现实问题进行单目标打击方案选择及发射地域分配:给定大批打击目标,每个目标都有若干单目标打击方案,每个单目标打击方案涉及的武器分属不同作战单位,而每个作战单位只能在有限的几个作战区域进行发射活动.在详细描述问题的基础上,将诸多决策因素作为约束条件或优化目标引入问题,给出了问题的数学模型,并基于问题的特征设计了问题求解的遗传算法,实验显示针对此类多约束、多目标大规模火力分配问题,能够很快得出分配方案,针对实际碰到的问题,能在1min内给出结果,大大提高作战任务规划效率.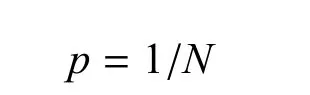

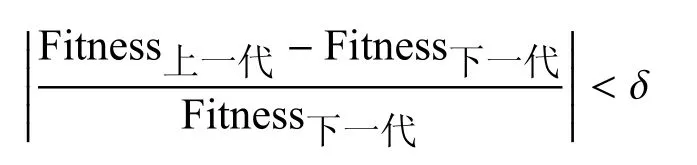
3.2 算法效率

4 结论

