神经网络的非脆弱状态估计

杨帆 董宏丽 李佳慧 安杏杏 邵晓光

几十年来,由于其自适应学习和逼近非线性函数的能力,递归神经网络(RNNs)已经成为研究焦点.到目前为止,各种递归神经网络的结构以及学习方案已经被用于分类、模式识别、回归和优化问题及许多实际应用领域,如系统的识别和控制,轨迹预测,决策和医疗诊断[1−2].另一方面,由于电子神经网络中放大器的有限开关速度和其他原因,通常使信号传输时产生时滞是不可避免的.如果没有适当的考虑,时滞将会引起系统振荡甚至不稳定.在过去的十年里,对于各种神经网络和其他网络时滞现象在动力学分析问题中得到了大量的研究关注[3−9].

对于神经网络的成功应用,往往是先了解可用于优化或控制的神经元状态的实际信息.然而,由于资源物理上可利用的限制,通常只有部分神经元状态信息可通过网络输出,尤其是大规模神经网络.因此,当务之急是通过可用的网络输出尽可能准确地估计神经元状态[10],由此产生的神经网络状态估计问题在过去的几十年中已经引起了广泛兴趣,已经有大量文章发表[11−16].例如文献[17]中设计的状态估计器是针对带有马尔可夫跳参数和时变时滞的离散神经网络.

在控制器/估计器应用过程中,通常情况下由于各种原因,例如数值舍入误差、计算机的有限字长和模数转换精度,实际执行的参数与期望的会略有不同.众所周知,即使是估计器的漂移、滤波器/控制器参数微小的变化都可能会导致整体动态系统发生巨大变化(如性能下降,甚至最终不稳定)[18−19],这种现象被称为是脆弱的.在过去的几年中,对于控制器/估计器在可接受的执行误差范围内,非脆弱性在保证所需系统性能方面已经成为一个越来越重要的性能指标[20−22].例如,文献[22]对于一类同时带有随机发生增益变化(ROGVs)和信道衰落的离散T-S模糊系统,设计了一个非脆弱H∞滤波器.

在神经网络非脆弱状态估计的背景下,一些初步的结果已经出现在文献中.例如,文献[23]对于带有混合时变时滞和马尔可夫跳参数的神经网络,设计了一个非脆弱观测器.很明显在文献[23–24]中设计的估计器/观测器的结构已经被假定类似于基础神经网络,以便随后的动力学分析.然而这样的假设意味着,为了估计器/观测器的应用具有实际意义,时变时滞和激励函数必须是完全已知的.遗憾的是,利用这种复杂的估计器/观测器是相当不方便的,因为在参数识别和工程实现时的限制很多.因此,我们通常的想法是在保证估计性能的前提下,设计一个结构简单、适用于实际应用的状态估计器,这也是本文研究的主要目的.

1 问题描述

考虑如下时滞神经网络系统:

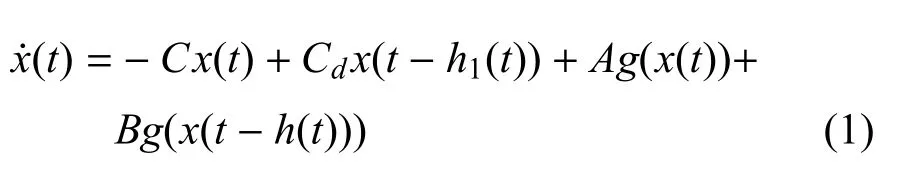
其中,x(·)=[x1(·),x2(·),···,xn(·)]T∈Rn是神经元状态向量,g(x(·))=?g1(x1(·)),g2(x2(·)),···,gn(xn(·))?T∈Rn是初始条件为g(0)=0的非线性激励函数,C=diag{c1,c2,...,cn}是正定对角矩阵,A,B,Cd分别是连接权矩阵、时滞连接权矩阵和常数实矩阵.h(t)和h1(t)分别是时变时滞和状态时滞.它们满足

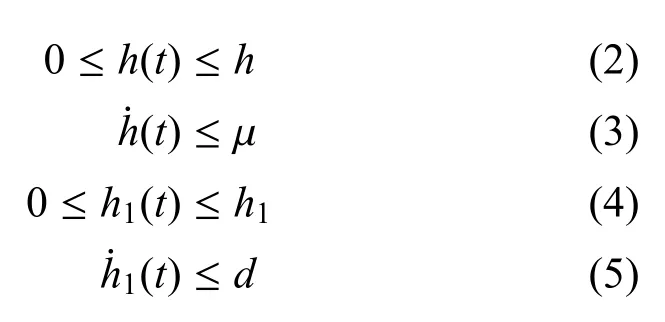
其中,h,h1,µ,d是常数.

假设1.对于任意的 α1,α2∈R,α1, α2,激励函数g(·)满足:

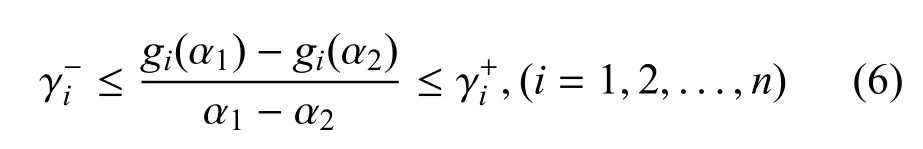
神经网络的测量输出表示为如下形式:

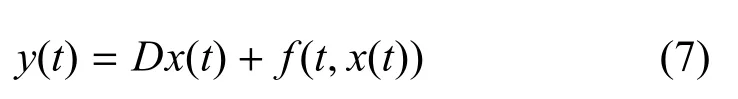
其中,y(t)∈Rm是测量输出,D∈Rm×n是已知常数矩阵.f(t,x(t))是作用在网络输出的初始条件为f(0,0)=0的神经元状态依赖非线性扰动.f(t,x(t))满足如下的Lipschitz条件:

其中,F=diag{f1,f2,...,fn}是已知的常数矩阵.

全阶非脆弱状态估计器的形式如下:

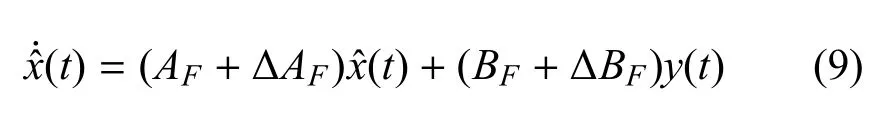
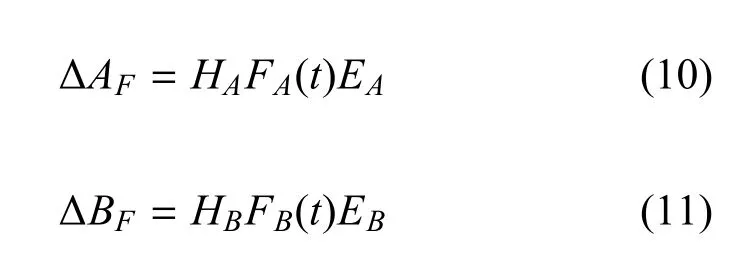
其中,HA,HB,EA和EB是已知适当维数矩阵,FA(t)和FB(t)是未知矩阵满足和

为了便于分析,定义如下:

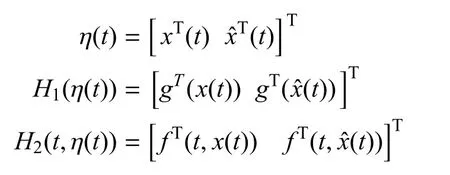
结合式(1)∼式(7)式及式(9),可以得到如下增广系统:

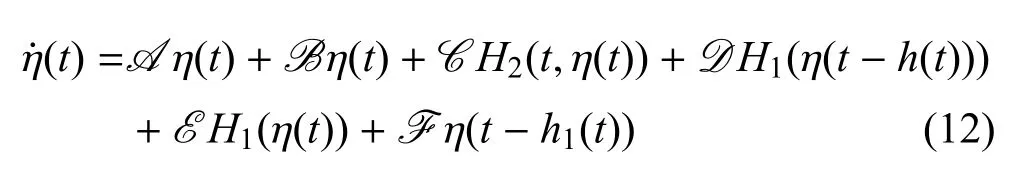
其中

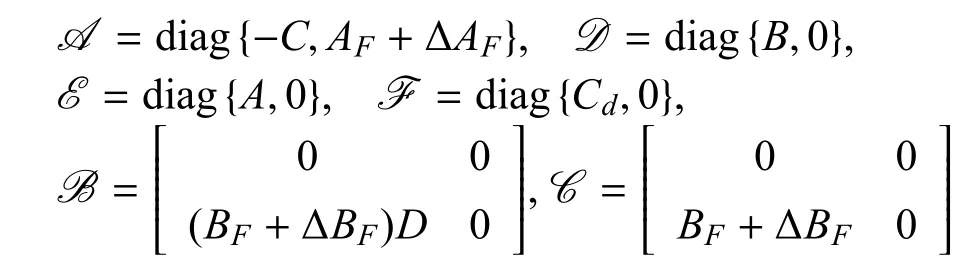
从式(6)和式(8)可以得到

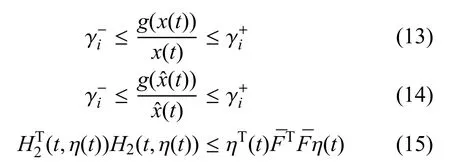
定义1.如果满足下列式子,则增广系统式(12)渐近稳定:

本文的目的是为连续神经网络式(1)设计一个非脆弱估计器,使增广系统式(12)渐近稳定.

2 主要结果

引理1[26].令M=MT,U和V是适当维数实矩阵,并且V满足VTV≤I,只要存在一个正定标量ε使M+εUUT+ε−1WTW<0或

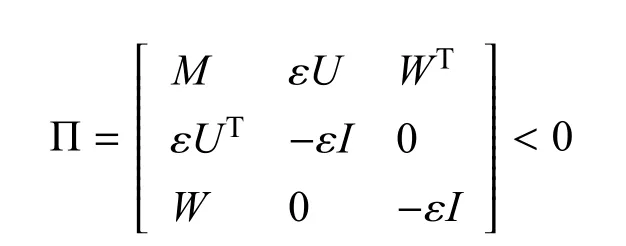
成立,则M+UVW+WTVTUT<0成立.

引理 2[2]. 假设Z= diag{β1,β2,...,βn} 是半正定对角矩阵,令x=[x1,x2,···,xn]T∈Rn,O(x)=[o1(x1),o2(x2),···,on(xn)]T是连续非线性函数且满足

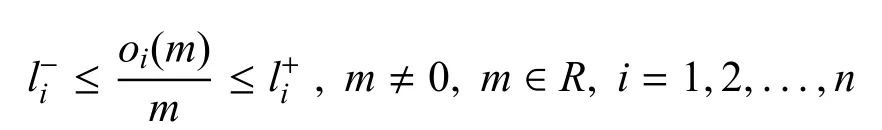
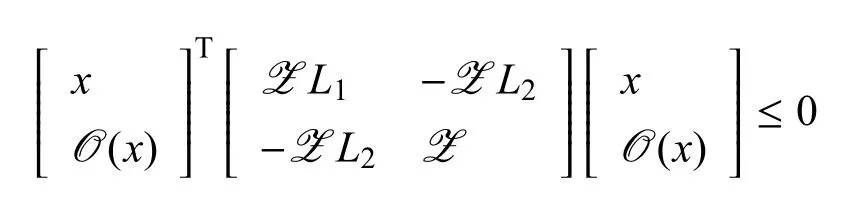
或者xTZL1x−2xTZL2O(x)+OT(x)Z O(x)≤0,其中

引理3[27].对于任意的正定矩阵R>0,常数h>0,如果存在向量函数x(t):[0,h]→Rn,使得积分有定义,则下面的不等式成立

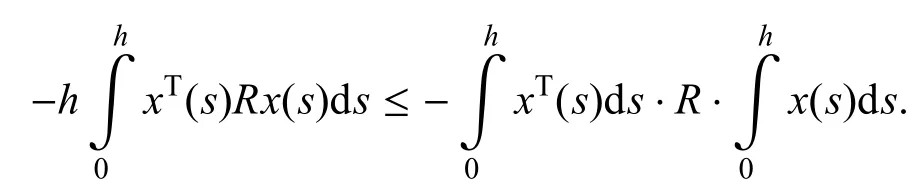
现在开始进行增广系统式(12)的稳定性分析.

定理1.考虑连续神经网络式(1)∼式(7),其包含时变时滞,非线性扰动和增益变量.估计器参数AF和BF已知.如果存在正定矩阵P>0,K>0,矩阵正标量ε1和4个对角矩阵L>0,H>0,J>0,Y>0,满足下列线性矩阵不等式(LMI):

则增广系统式(12)渐近稳定,其中

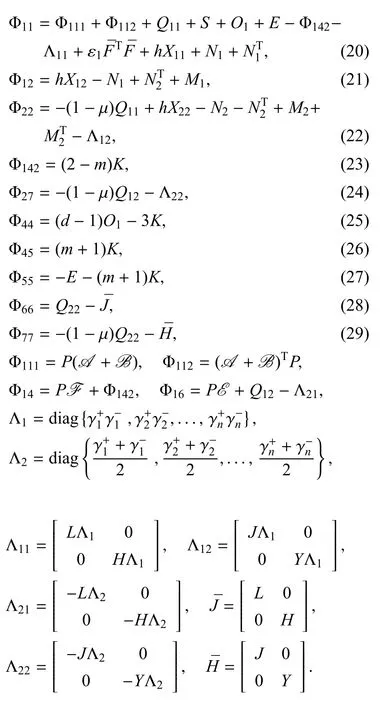
证明:构建如下Lyapunov函数:

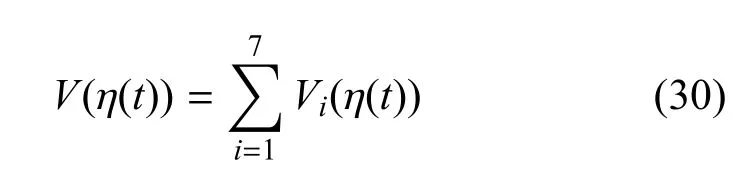
其中,V1(η(t))= ηT(t)Pη(t)

沿式 (12)的轨迹计算式 (30)中Vi(η(t))(i=1,2,...,7)的导数得(η(t))=2ηT(t)P(t)

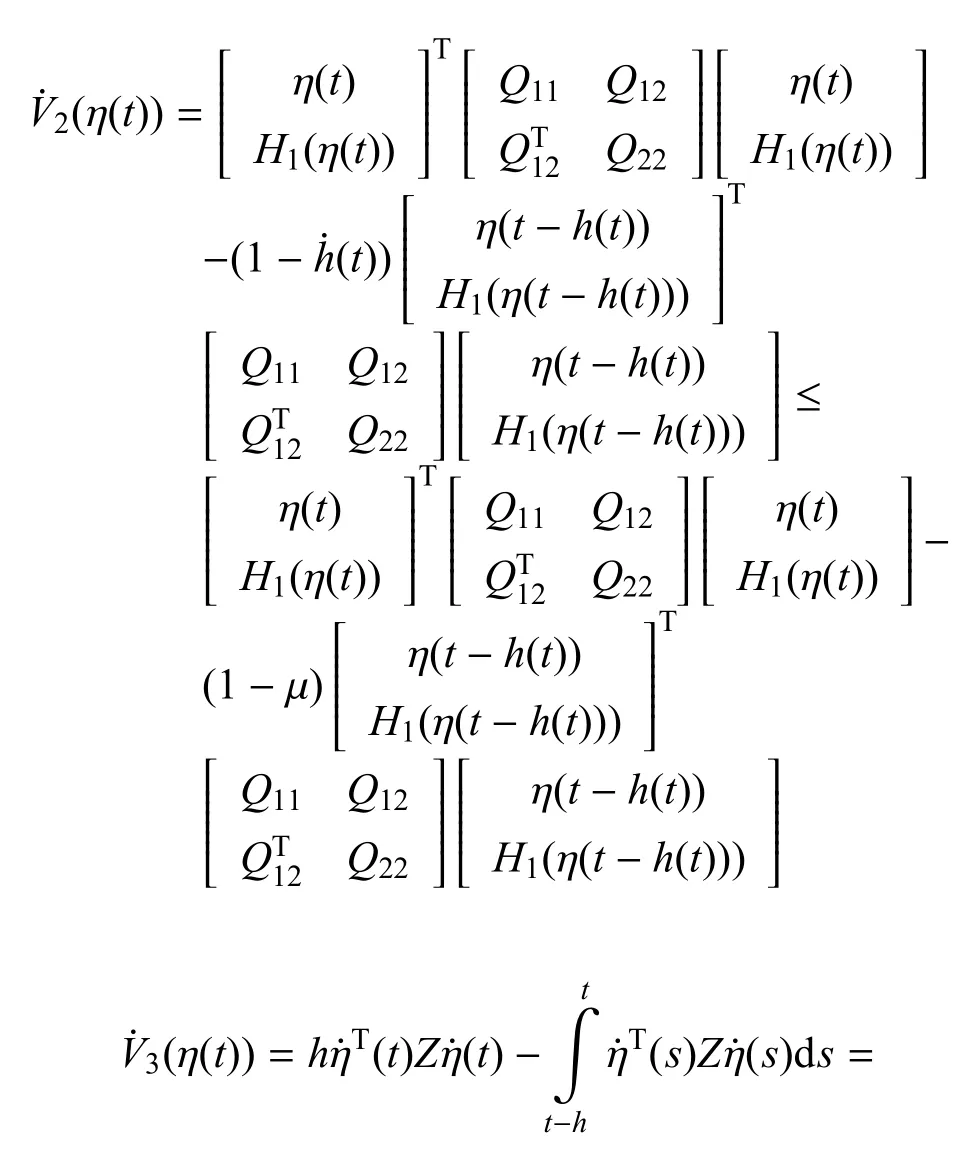
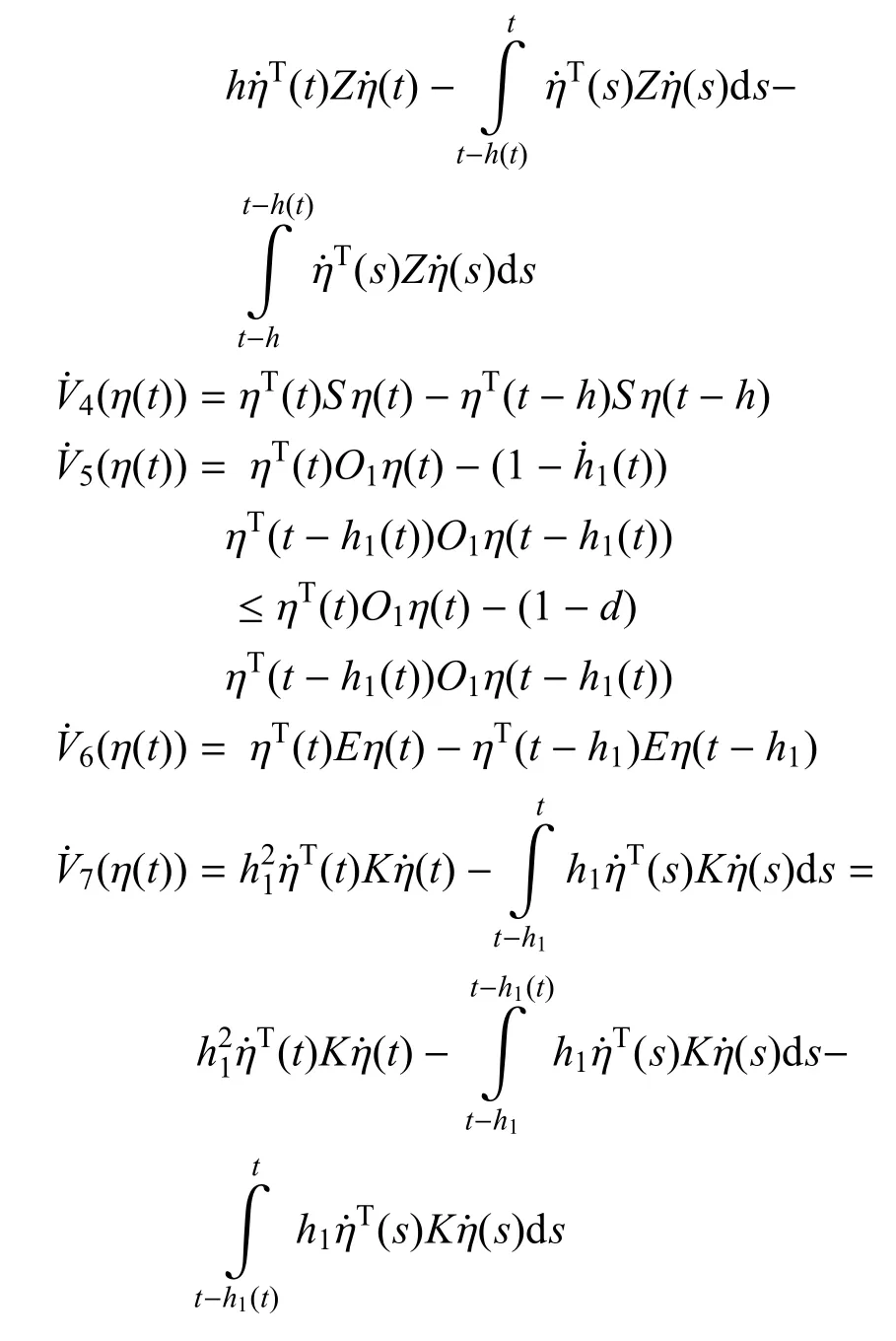
令m=h1(t)/h1,可以得到

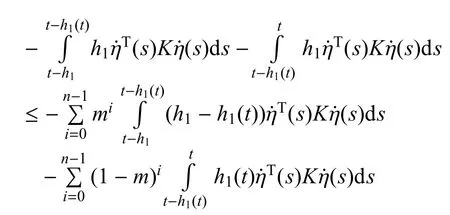
令上述不等式中n=2,同时利用引理3可以得到

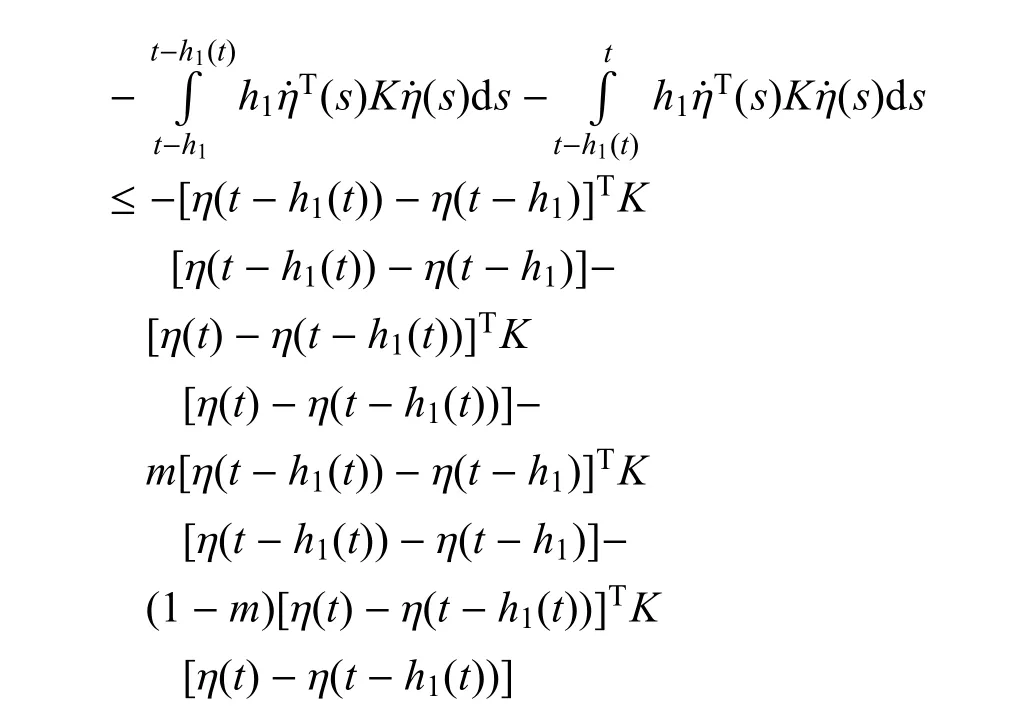
对适当维数的矩阵M和N利用Leibniz-Newton公式,可以得到如下等式:

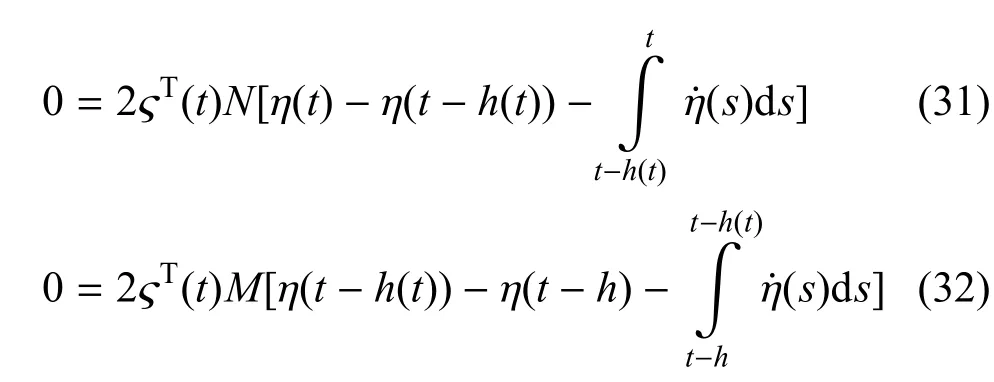
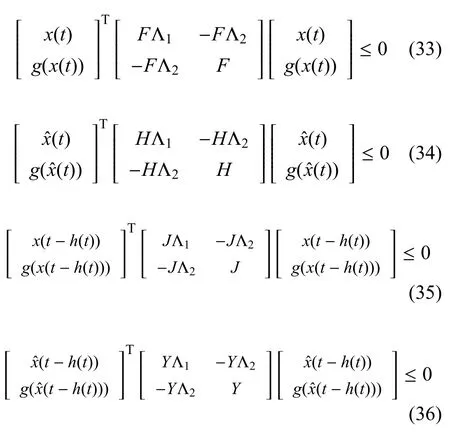
然后由假设1和引理2得到由式(33)∼式(36)进一步得到

此外,根据条件式(15),对于正标量ε1推断出

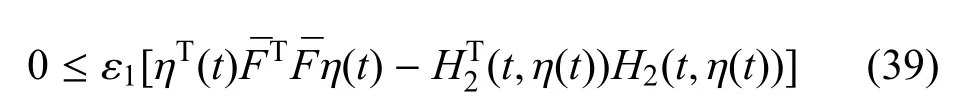
对任意适当维数的矩阵X=XT可以得到

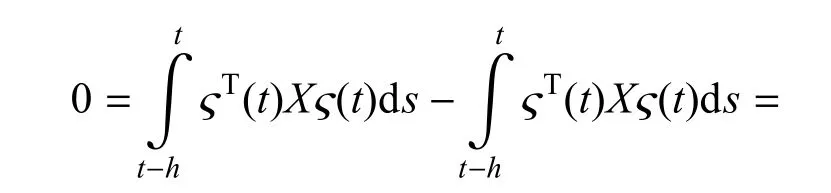
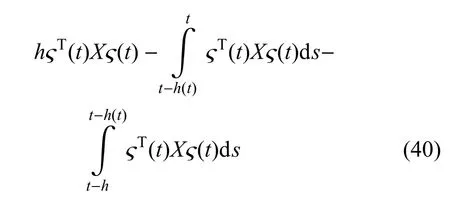
将式(31)∼式(32)、式(37)∼式(40)的右侧加到Vi(η(t))(i=1,2,...,7)的导数中,得到

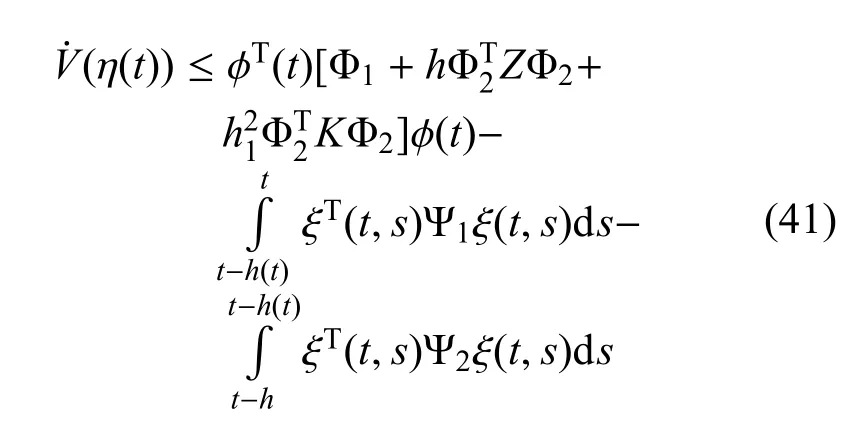
其中

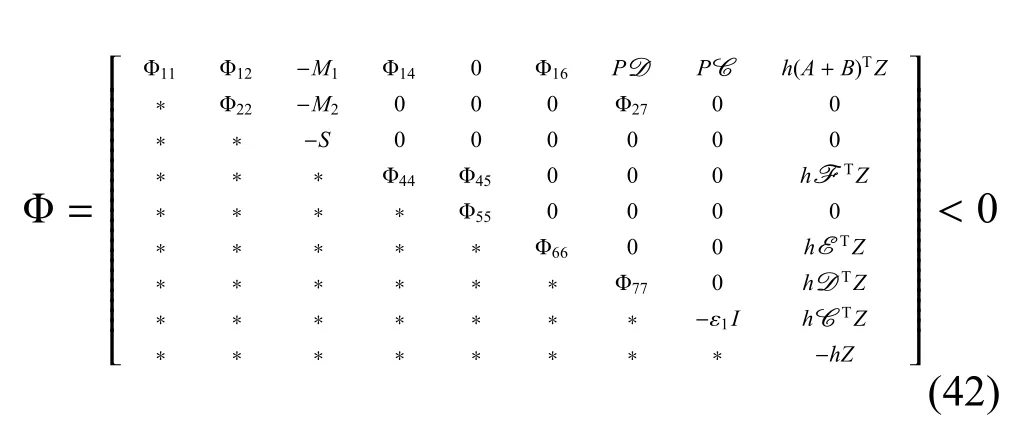
观察到(P−Z)TZ−1(P−Z)=PZ−1P−2P+Z>0,推出PZ−1P≥2P−Z.然后由(17)式得到(43)式成立.令然后得到α0<0并且满足下式

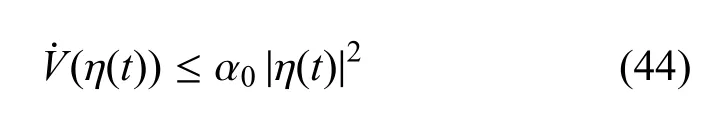
两边取0到T(T>0)积分,得到

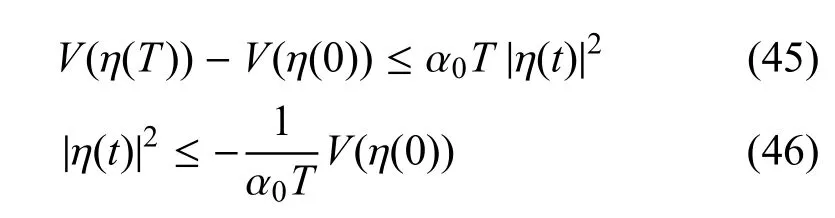
因为|η(t)|2是收敛的,从而得出结论

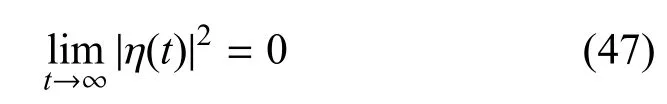
根据定理1的研究结果,下面设计时滞神经网络系统式(1)的状态估计器.

定理2.考虑连续神经网络式(1)和估计器增益变量式(9).如果存在正标量ε1>0和ε>0,正定矩阵Z>0,S>0,O1>0,E>0,K>0,矩阵N=4个对角矩阵L>0,H>0,J>0,Y>0,ZA和ZB同时满足式(18),式(19)和下面不等式:

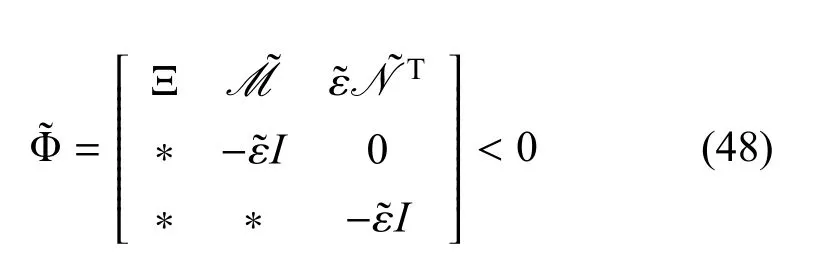
则增广系统式(12)渐近稳定,其中

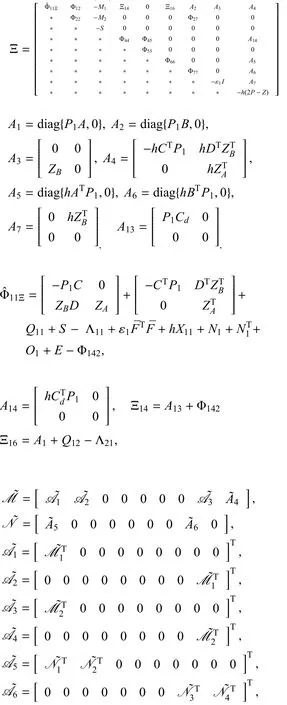
并且 Φ12,Φ22,Φ142,Φ27,Φ44,Φ45,Φ55,Φ66和Φ77分别在式(21)∼式(29)式中已定义.形如式(9)的估计器增益可以通过求出.

证明:根据定理1,为了证明系统式(12)的渐近稳定性,式(48)足以代替式(17).所以用式(12)中定义的A,B,C,D,E和F代替式(17)中的ˆΦ,从而得到

其中

另一方面令ZA=P2AF和ZB=P2BF.然后,∆Ξ可被拆分成:

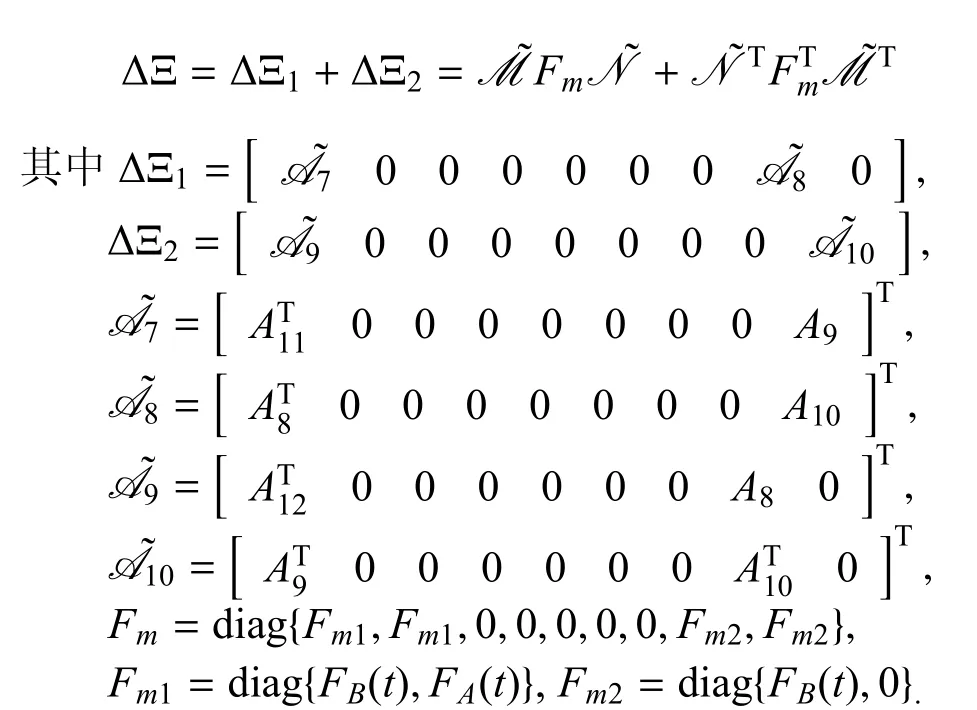
到目前为止,可以将式(17)重新写成如下形式:

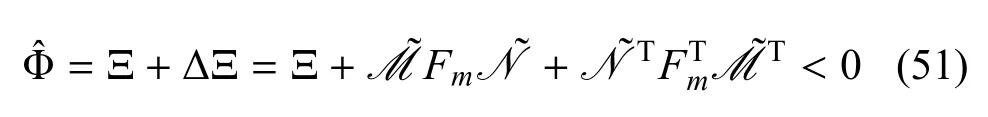
根据引理1如果存在一个正标量ε使

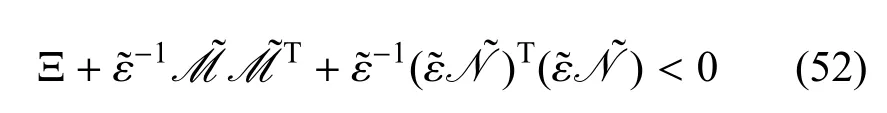
成立,则式(17)成立.根据Schur Complement引理,当且仅当式(48)成立时,式(52)成立.最后,可以得出这样的结论:由式(48)可以得到式(17)成立,根据定理1可以得出系统式(12)渐近稳定.此外,估计器增益可以从ZA=P2AF和ZB=P2BF中求得.

注释:定理2的研究结果中包含系统中的全部物理参数,如时滞边界、刻画增益不确定的矩阵等.通过求解不等式(18)、式(19)和式(48)的可行解,可以计算出期望估计器的增益.

3 数值仿真

给定时滞神经网络系统式(1)的参数如下:

h(t)=4,h1(t)=0.5,G=0.5I.

网络测量输出式(7)中参数为D=I,F=0.4I,估计器增益变量中的参数为:

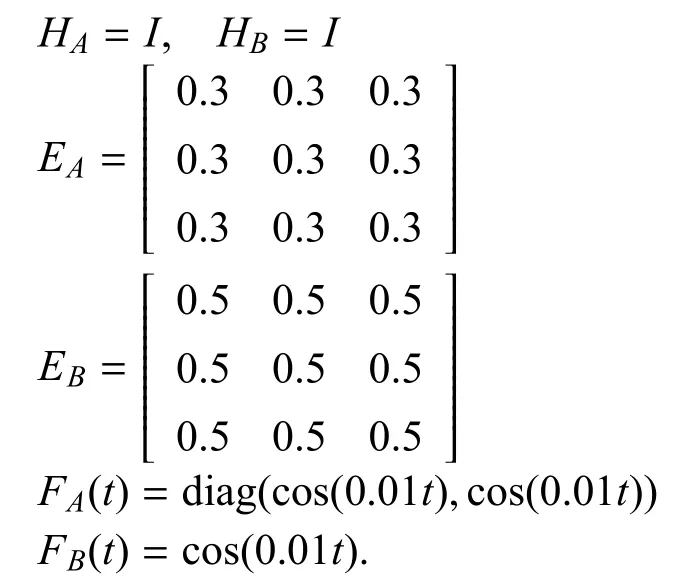
选取的激励函数为:g1(x1(t))=−tanh(0.4x1(t))

g2(x2(t))=0.2tanh(x2(t))

g3(x3(t))=tanh(0.6x3(t))

与神经元状态相关的非线性扰动为f(t,x(t))=0.0004cos(x(t)).

利用MATLAB软件,经过运算,求解出估计器增益矩阵如下:

仿真结果如图1∼图4.图1∼图3分别描述的是神经网络的状态向量x1(t),x2(t),x3(t)和它们的估计向量x1(t),x2(t),x3(t).图4描述的是状态向量与估计向量之间的误差.通过仿真结果验证了增广系统的渐近稳定性.

图1 状态向量x1(t)和它的估计x1(t)

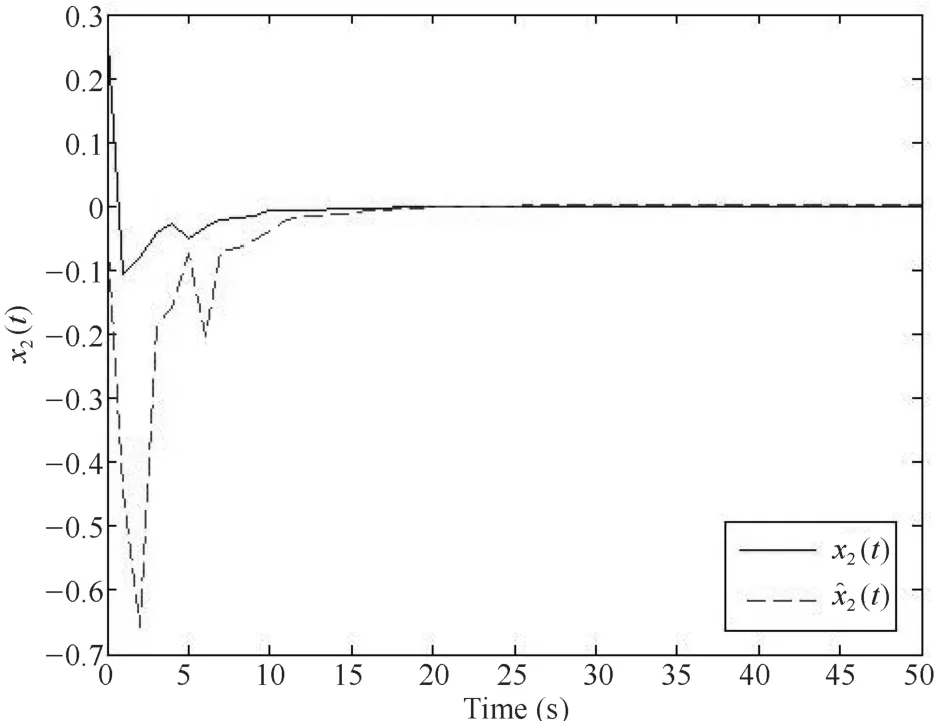
图2 状态向量x2(t)和它的估计x2(t)

4 结论

本文研究了带时变时滞和非线性扰动的神经网络的状态估计问题.通过李雅普诺夫稳定性理论和求解几个LMI得到估计器增益矩阵,进而得出保证增广系统渐近稳定的充分条件.最后通过数值仿真证明了该方法的有效性.值得期待的是我们的主要结论可以推广到更普遍或实际的系统中,例如Itˆo型随机系统[28],非线性马尔可夫跳系统[29−30],航天器姿态控制系统[31],不确定随机系统[32],采样数据系统[33],有限时域非线性系统[34−35],并且在不久的将来会出现与其相应的结果.此外,这里的方法可以进一步处理故障检测问题[36],以及更复杂的神经网络非脆弱状态估计问题,如具有测量衰减[37−39]和不完全测量[40−41]的神经网络.

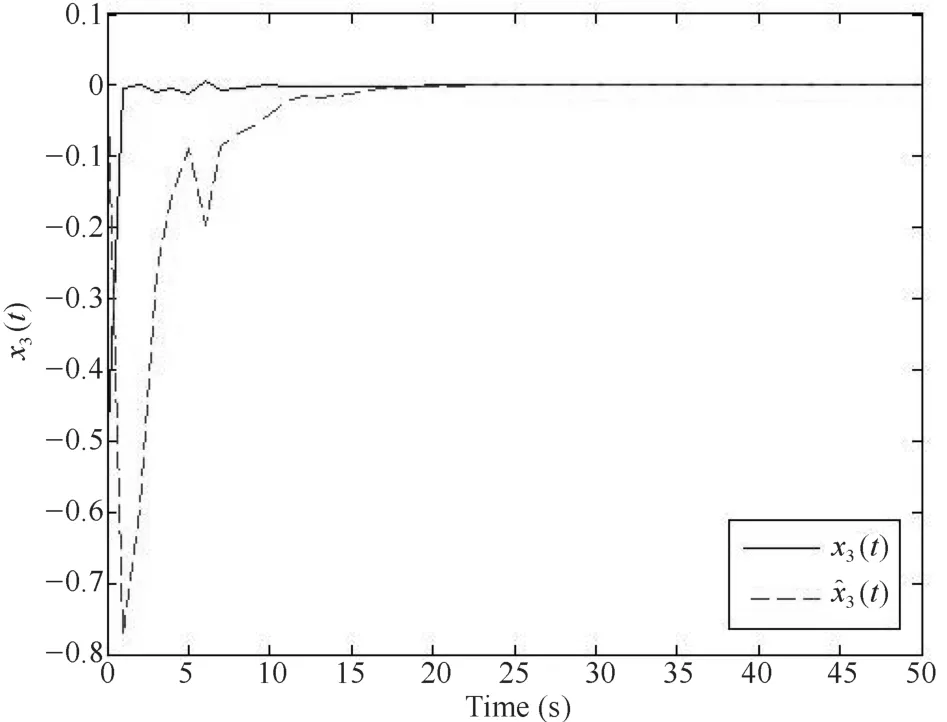
图3 状态向量x3(t)和它的估计x3(t)

图4 状态向量和它的估计之间的误差