具有随机干扰的单种群间歇扩散模型∗
年巧玲,张龙,李宝雄
(新疆大学数学与系统科学学院,新疆乌鲁木齐830046)
0 引言
在自然界中,斑块环境下种群的扩散现象是非常流行的[1].由于环境的改变和人类的活动,为了选择更适宜的生存环境,种群将扩散或迁移到其它斑块.通过建立数学模型,种群的扩散问题能够被很好的解决,因此,扩散模型被许多专家和学者广泛研究.起初,人们认为扩散现象时时刻刻发生,继而专家们[2,3]建立了连续扩散模型,使得世人对扩散现象有了初步的了解.后来,人们发现连续扩散模型不能很好地描述一些种群特定生物现象,基于对上述讨论的改进以及脉冲微分方程的发展,专家们[4,5]研究了脉冲扩散模型.
众所周知,上述模型都是确定的,他们的缺陷是没有考虑外部因素对种群性质的影响,基于环境噪音,出生率,环境容纳量,竞争系数以及其它参数,专家们[6,7]研究了随机扩散模型.当前,对确定模型的内禀增长率和密度制约系数进行白噪声扰动的文章已经很多,但对种群扩散率进行扰动的文章却几乎不见,再考虑到真正生态环境中种群扩散现象的间隙性(即不是连续的,也不是瞬间完成的),对人们来说,建立具有白噪声扰动的间歇性扩散模型是合理的.
基于上述讨论,在本文,对扩散率进行随机扰动,即Dij(t)能够被代替
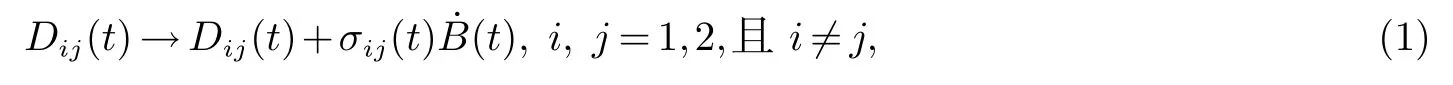
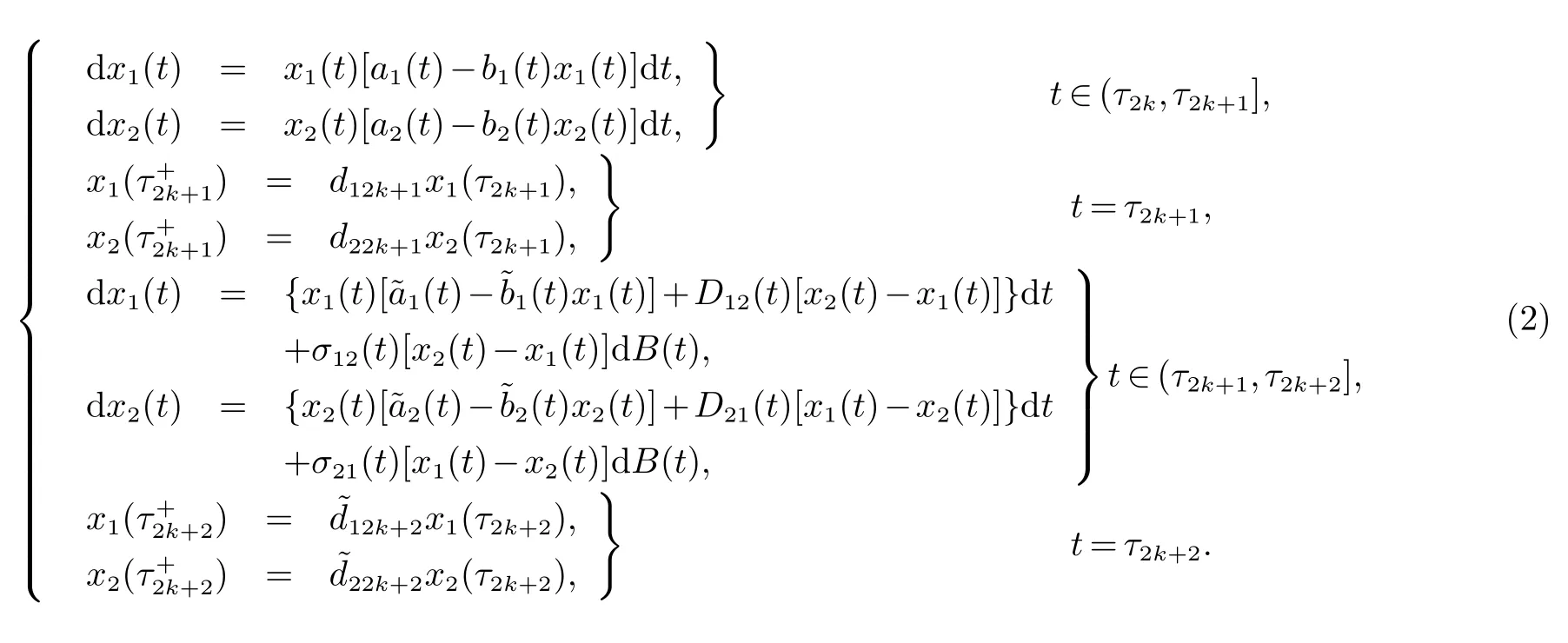
这里xi(t)代表种群在第i个斑块密度,ai(t)和(t)分别代表在t∈(τ2k,τ2k+1]和t∈(τ2k+1,τ2k+2]时种群x在第i个斑块的内禀增长率,bi(t)和(t)分别代表在t∈(τ2k,τ2k+1]和t∈(τ2k+1,τ2k+2]时种群x在第i个斑块的密度制约系数,Dij(t)代表种群x从第j个斑块到第i个斑块的扩散系数,dik+1和分别代表在时刻τ2k+1和τ2k+2时种群x的剩余率,τk为一个满足
1 预备知识
贯穿全文,如果v(t)是t∈R+上连续函数,定义
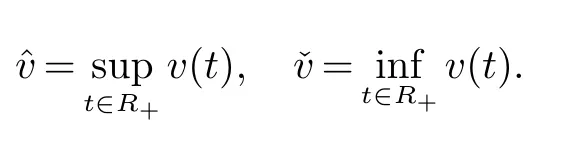
x2维列向量.
(a,b)T向量(a,b)的转置.
二维正半平面,
a∧ba与b的最小值.
∞正无穷.
∅空集.
R+正实数空间.
R 实数空间.
设(Ω,F,{Ft}t≥0,P)为一个完备的概率空间,并且相应的滤子满足通常条件(它是右连续且F0包含所有的P零集),B(t)为此概率空间上的标准布朗运动.定义x(t)=(x1(t),x2(t))T,并且
定义1[8]如果对任何的ε∈(0,1),存在一个常数H=H†,使得系统(2)具有初值的任何正解x(t)=(x1(t),x2(t))T满足

那么,称系统(2)随机最终有界.
为了讨论方便,系统(2)能够被写为如下形式:
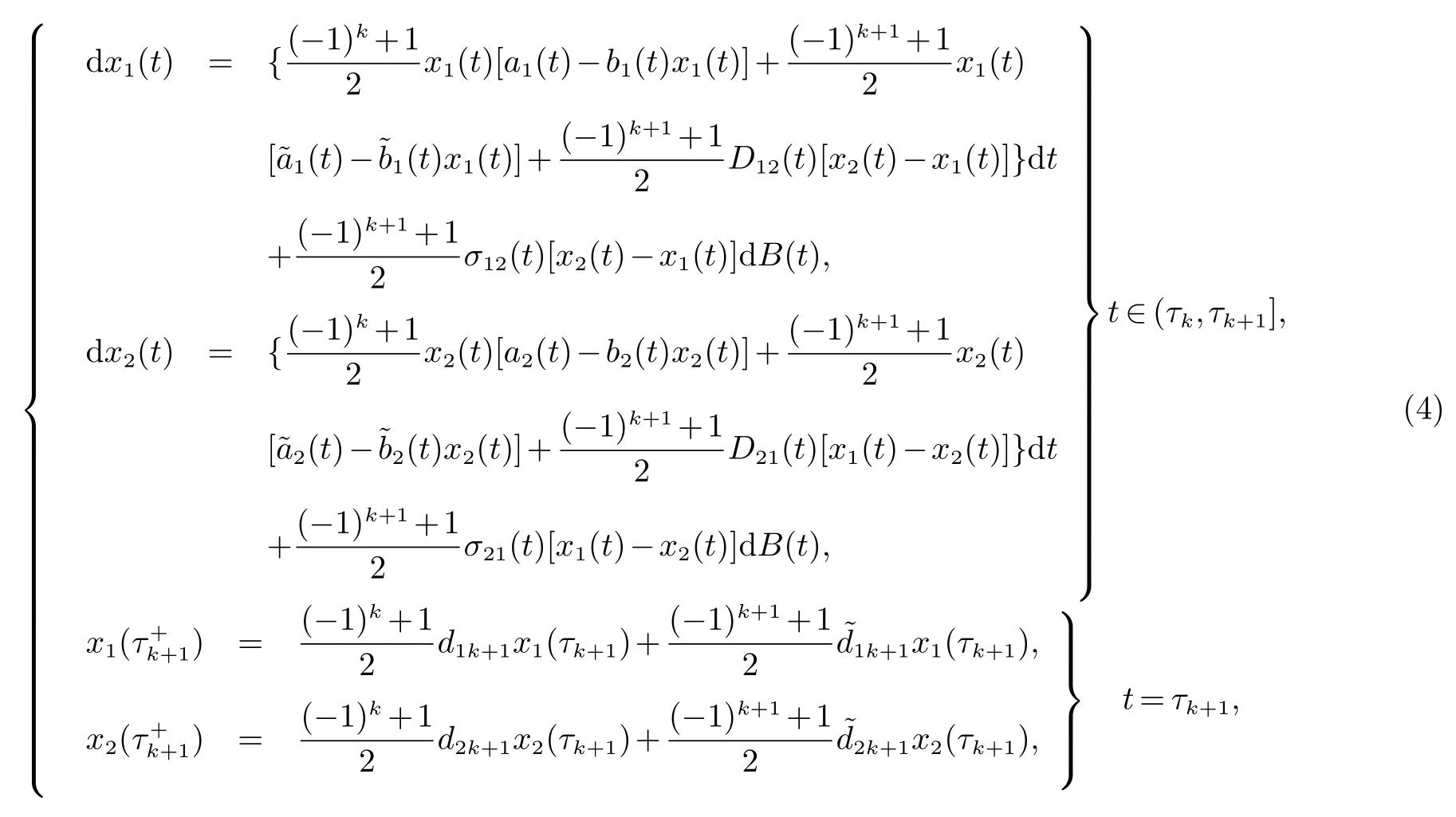
在这篇文章中,对系统(4),可以做如下假设:
(H1)上为连续有界函数.
(H2)
(H3)系统(4)的剩余率dik+1,(i=1,2,…)满足
(ii)αk+1=
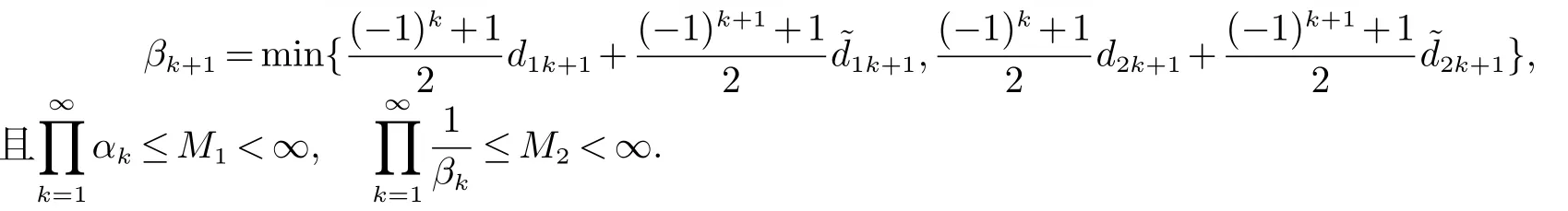
2 主要结果
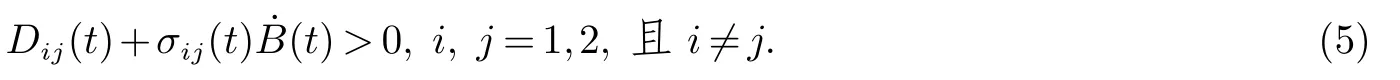
证明因为系统(4)的系数满足局部Lipschitz条件,所以对任意给定的初始条件存在唯一的最大局部解x(t) 定义在t∈[)上,其中ρe为爆炸时刻.当t∈(τ0,τ1],系统(4)的解xi(t)>0,(i=1,2).当t∈(τ1,τ2],其初值xi()=di1xi(τ1)>0,如果xi(t)>0(i=1,2),满足系统(4)的解为正值.若出现xi(t)=0,那么对j=i
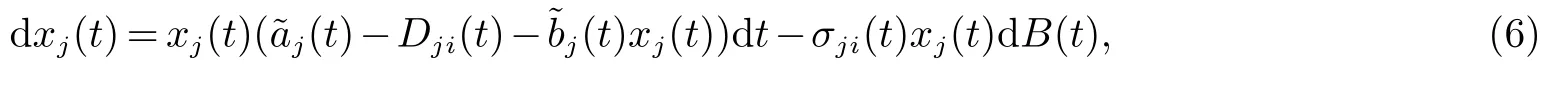
方程(6)的解xj(t)>0,故很容易可以得到
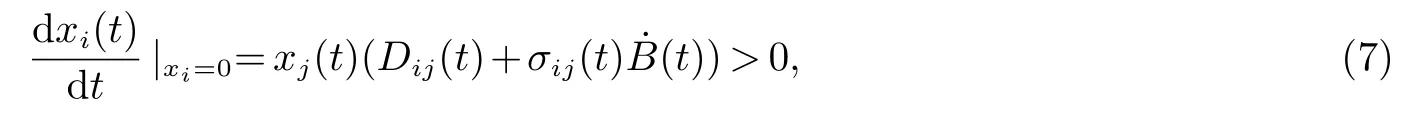
故系统(4)的解在t∈(τk,τk+1]上为正值.由归纳法得系统(4)的解在t∈[)上为正值.为了证明此解的全局性,只需证明ρe=∞a.s即可.为此,令k0>0充分大,使得所有意整数k≥k0,定义停时
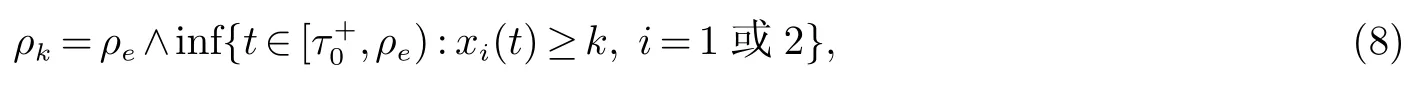
总是约定infφ=∞,显然ρk关于k是单调增加的,现在只需证明ρ∞=∞.若此结论不真,则存在T>0和ε∈(0,1)使得

于是存在整数k1≥k0满足

定义函数V:R2+→R+如下
《普通高中生物学课程标准(2017版)》(以下简称新课标)的基本理念是:以“生命观念、科学思维、科学探究和社会责任”学科核心素养为宗旨,内容聚焦大概念,教学过程重实践,关注学生主动参与,关注学生实践,动手结合动脑。教师围绕着生物学大概念来组织并开展教学活动,通过设置合理的教学情境,基于学生动手活动或对资料的分析及探究,将有助于学生对知识的深入理解和迁移应用,有利于促进学生对生物学概念的建立、和应用理解。

对任何k≥k1,存在一个ik使得由公式,
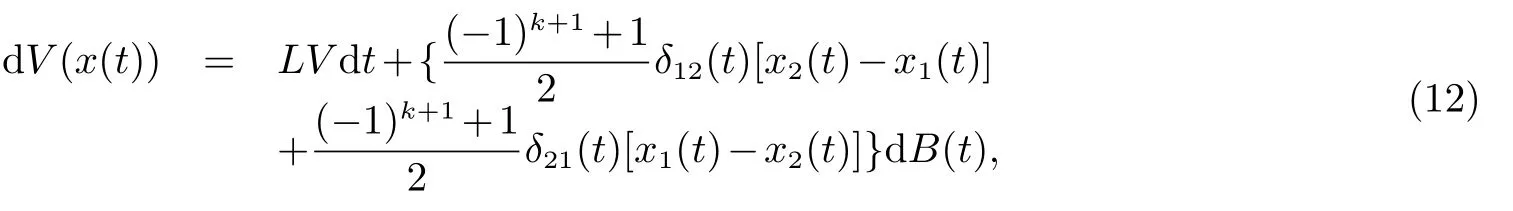
这里LV是一个的算子,被定义为
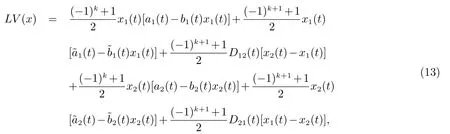
由假设(H1),(H2),能够得到

将(14)带入(12)得
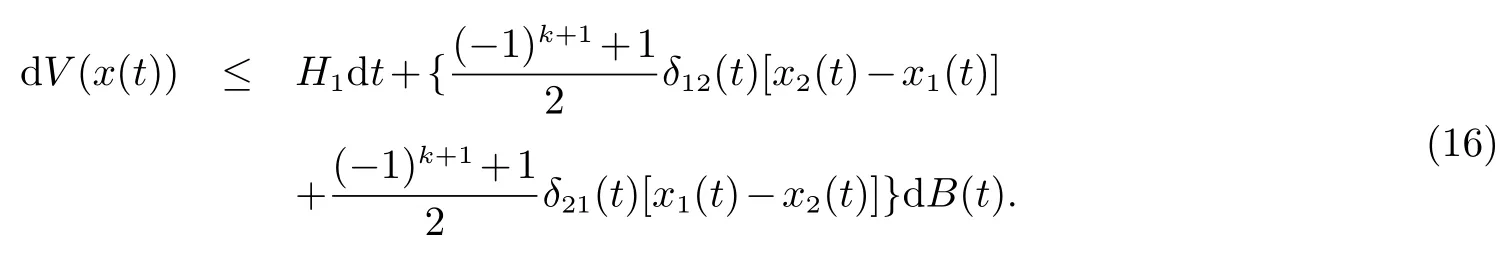
对任何T>0,对上式两边从积分取期望
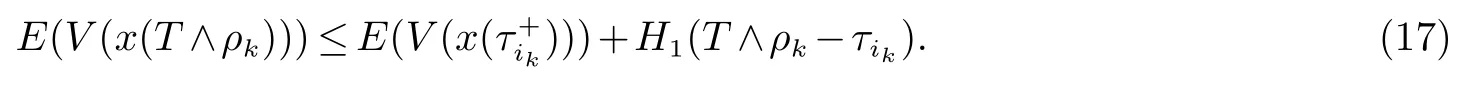
由假设(H3)
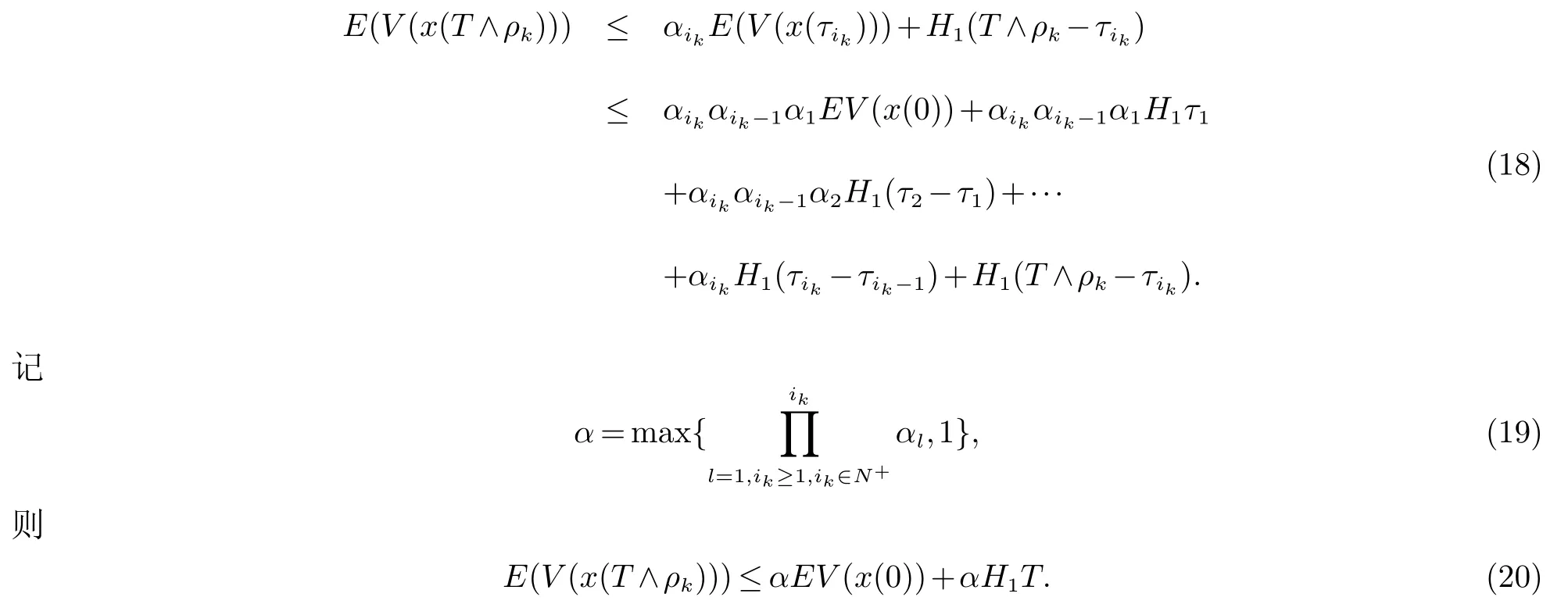
令Ωk={ρk≤T},则由(10)推出P(Ωk)≥†,注意到对任意ω∈Ωk,xi(ρk,ω)≥k.因此
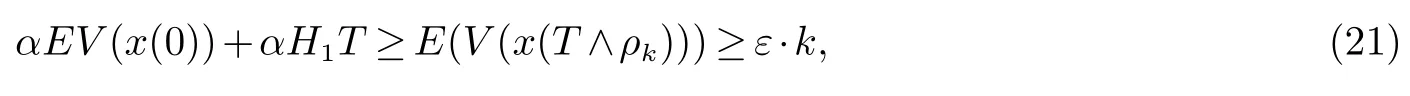
令k→∞,导出矛盾

定理2基于假设(H1),(H2),(H3),存在常数K,使得对任何初值系统(4)的解x(t)=(x1(t),x2(t))T满足

证明由定理1,系统(4)的任何解x(t)=(x1(t),x2(t))T在t∈R+上仍为正值.定义一个函数V:+

对任何t∈R+,存在一个正整数k∈z+使得t∈(τk,τk+1],由公式
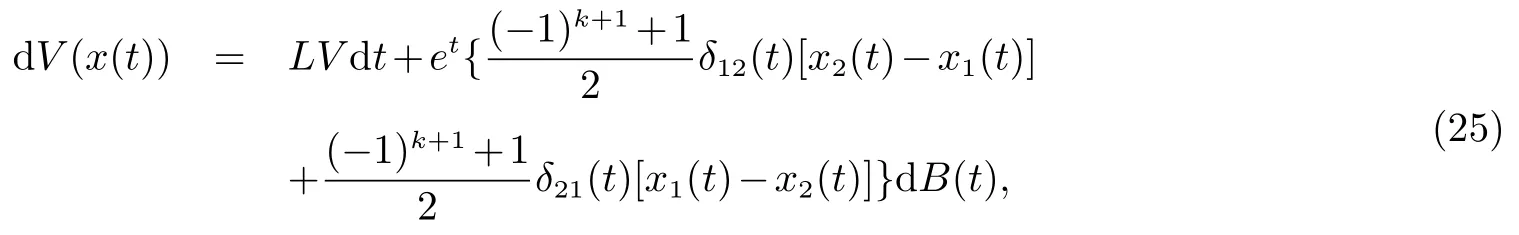
这里LV是一个的算子,被定义为
由假设(H1),(H2)

其中
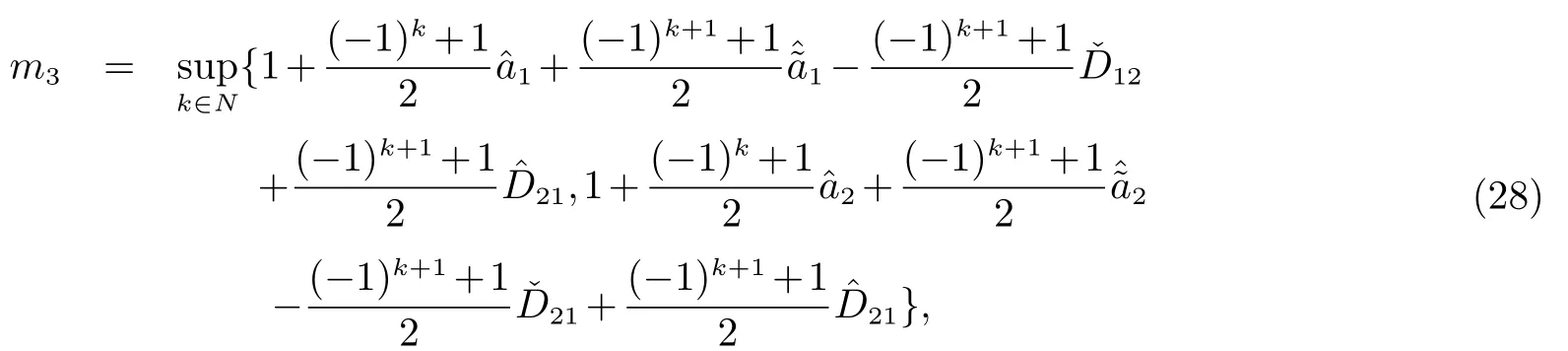
因此,将(27)带入(25)得
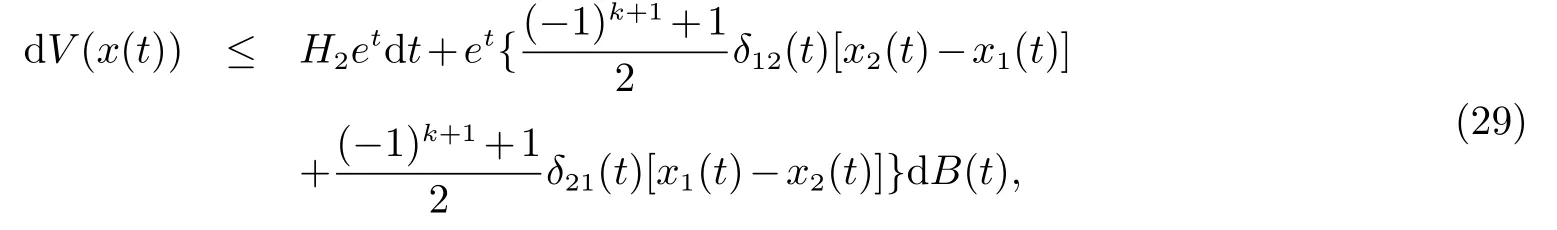
对上式两边从积分取期望
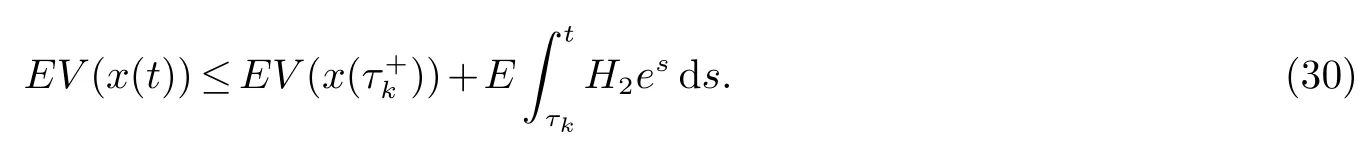
由假设(H3)
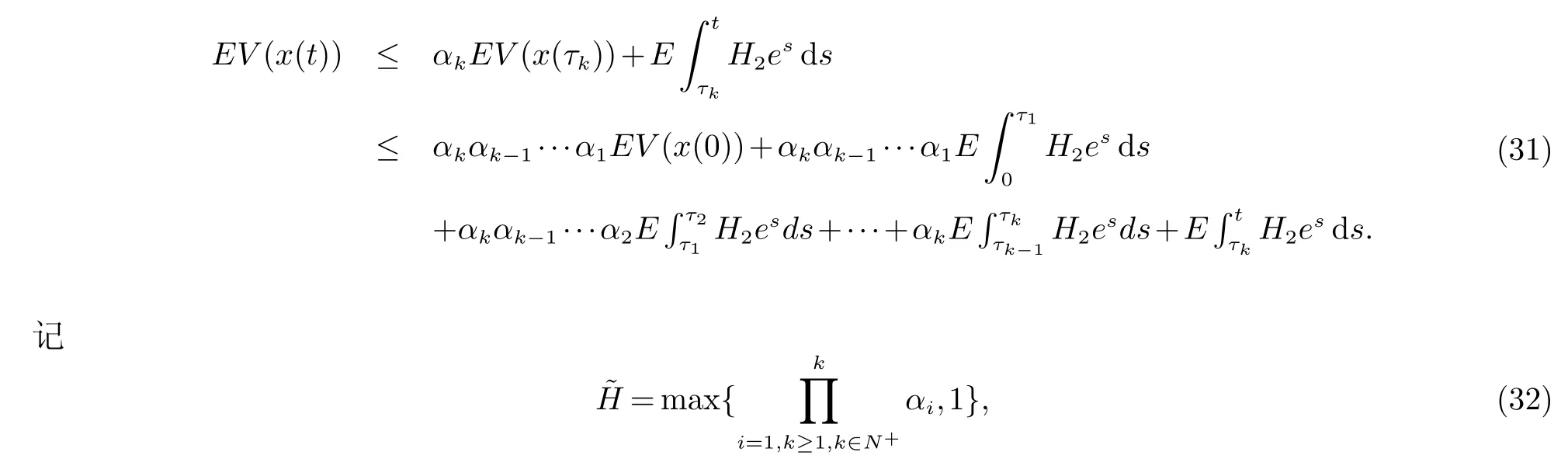
将(32)带入(31)得
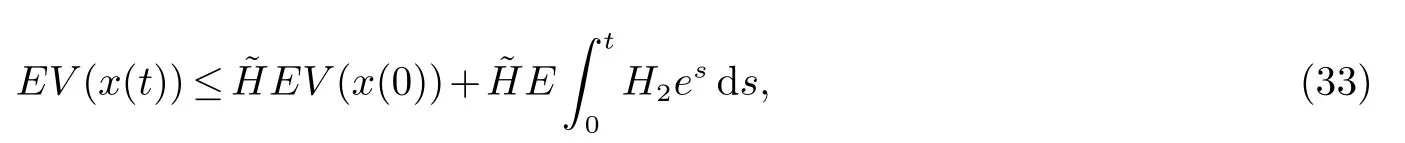
由不等式
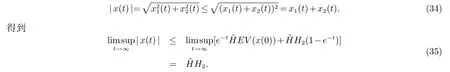


上式两边取上极限

因此

- 新疆大学学报(自然科学版)(中英文)的其它文章
- On the Page Number of Lexicographic Product of Paths and Cycles in Books∗
- Community Diversity and its Seasonal Dynamics of Soil Mites in Oasis of the Sangong River Watershed of Xinjiang,China∗
- 新疆伊犁铁列克特金矿床流体包裹体特征分析∗
- 工业企业规模、分布与区域经济增长∗
- Hartman-Wintner Theorem on the Noncommutative Hardy Spaces∗
- Laplacian Spectral Characterization of Graphs with Exactly Two Laplacian Eigenvalues Greater than Two∗

