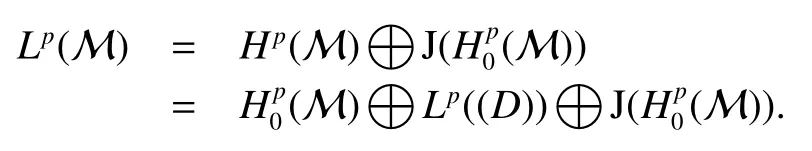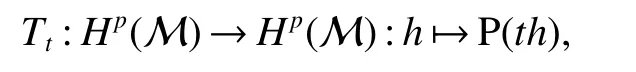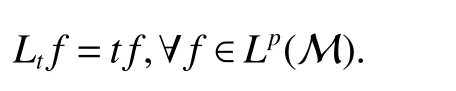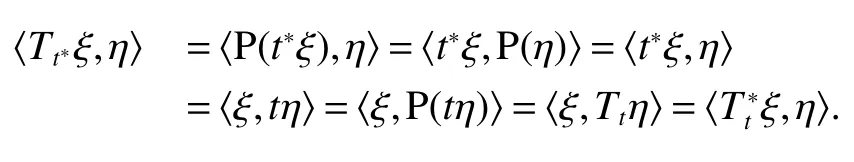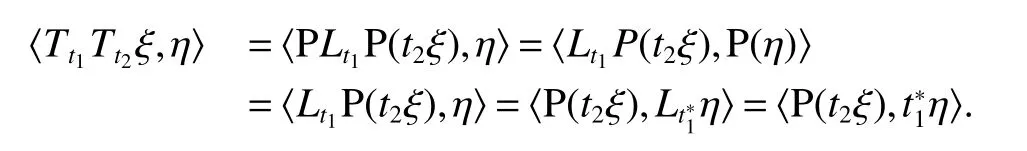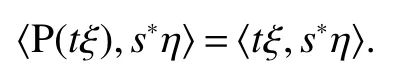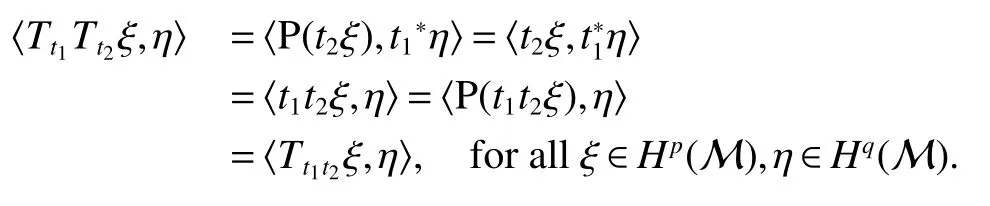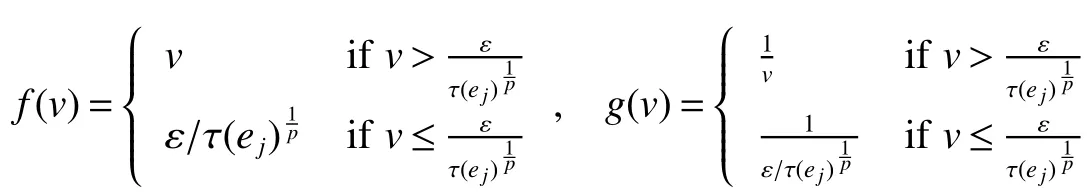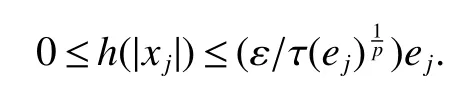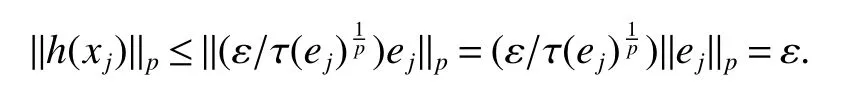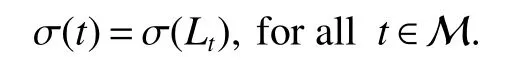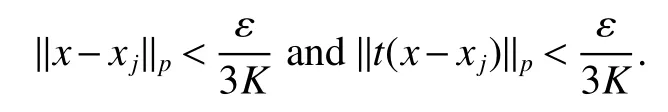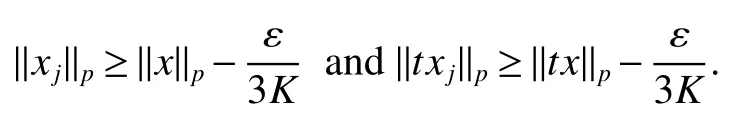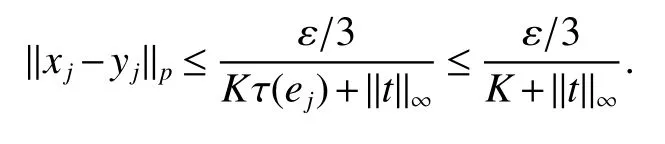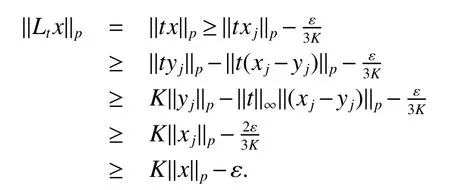Hartman-Wintner Theorem on the Noncommutative Hardy Spaces∗
YAN Cheng,Turdebek N Bekjan
(College of Mathematics and System Sciences,Xinjiang University,Urumqi Xinjiang 830046,China)
Abstract: Let M be a semi finite von Neumann algebra and Hp(M)be a noncommutative Hardy space associated with M.We prove that Hartman-Wintner spectral inclusion properties of Toeplitz operators is valid on Hp(M).
Key words:Semi finite von Neumann algebra;Noncommutative Hardy space;Toeplitz operator;spectrum
0 Introduction
In 1967,Arveson[1]introduced the notion of maximal subdiagonal algebras A of M,as noncommutative analogues of weak-∗Dirichlet algebras.This concept uni fies the analysis of several classes of nonselfadjoint operator algebras.Subsequently,Arveson’s pioneering work was extended to different cases by several authors.
In 1997,Marsalli and West[2]de fined noncommutative Hardy spaces for finite von Neumann algebras and obtained a series of results including the Riesz factorization theorem,the duality ofHp(M)andHq(M)and so on.In particular,Marsalli and West[3]de fined Toeplitz operators onH2(M)and obtained the Hartman-Wintner spectral inclusion theorem for those Toeplitz operators.L.E.Labuschagne and Q.Xu[4]establish the Helson-Szegtheorem for subdiagonal subalgebras and apply it to characterise the symbols of invertible Toeplitz operators.In[5],C.Yan and T.N.Bekjan discuss some properties of Hypenormal Toeplitz operators associated with semi finite von Neumann algebras.This paper is devoted to the study of Toeplitz operators on noncommutativeHp(M)associated with a semi finite von Neumann algebra M.
The organization of the paper is as follows.Section 1 contains several preliminary de finitions.In section 2,we get the Hartman-Wintner spectral inclusion properties.
1 Preliminaries
Throughout this paper,M denotes a semi finite von Neumann algebra with a normal semi finite faithful trace τ.Letx=u|x|be the polar decomposition ofx.Letr(x)=u∗uand ‘(x)=uu∗.We callr(x)and ‘(x)the left and right supports ofx,respectively.Ifxis selfadjoint,then‘(x)=r(x).This common projection is then called the support ofxand denoted bys(x).Let S+(M)={x∈M+:τ(s(x))<∞}and S(M)be the linear span of S+(M).A projectioneis said to be of finite trace if τ(e)< ∞.The elements of S(M)are said to be supported by projection of finite trace(see[6]).We will often denote S(M)simply as S.We de fine kxkp=(τ(|x|p))1/p,x∈ S.LetLp(M)be the closure of S with thep-norm,where 0 • A+J(A)is σ-weakly dense in M; • E(xy)=E(x)E(y),for allx,y∈A; • τ◦E=τ. A is said to be a maximal subdiagonal algebra in M with respect to E in the case that A is not properly contained in any other subalgebra of M which is subdiagonal with respect to E.Ji proves that a semi finite subdiagonal algebra A is automatically maximal in[8].This maximality yields the following useful representation of A: In this section we present our noncommutative Hartman-Wintner spectral inclusion theorem.Supposex∈Lp(M)and 1 For all 1 Let 1 •P2=P; •Ker(P)=J(M)); • τ(P(x)y)=τ(xP(y)),for allx∈Lp(M),y∈Lq(M),i.e.P∗=P. De finition 1Let 1 where P is the Riesz projection fromLp(M)ontoHp(M). The(left)multiplication operatorLtis de fined as ThenTt(h)=(P◦Lt)(h),∀h∈Hp(M).So Proposition 1Let 1 (1)(Tt)∗=Tt∗,for allt∈ M; (2)Tt1Tt2=Tt1t2,wheret2∈A ort1∈A∗. Proof(1)Let ξ∈Hp(M),η∈Hq(M).Then (2)Let ξ∈Hp(M),η ∈Hq(M).We have Ift2∈A,thent2ξ∈Hp(M).Thus Ift1∈A∗,then∈Hq(M),and so Therefore, That isTt1Tt2=Tt1t2. Since D is a semi finite von Neumann subalgebra,we can choose an increasing family of{ej}j∈Λof τ finite projection in D such thatej→1 under the strong operator topology,where 1 is identity of M(see[9]).The reduced von Neumann algebrasejMejandejAejare denoted by Mjand Aj,respectively.Then Ajis a maximal subdiagonal subalgebra of Mj.Indeed,de fine Ej(·)=ejE(·)ej,then Ejis a faithful normal expectation from Mjonto the diagonal von Neumann algebra Dj=Aj∩ J(Aj).Also,Aj+J(Aj)is σ-weakly dense in Mj;Ej(ejxejyej)=Ej(ejxej)Ej(ejyej),for allx,y∈ A;and τj◦Ej= τj(see[4,9]).Considering the elementxin reduced von Neumann algebra Mj,if there existsyin Mjandxy=ej=yx,then we callxis invertible in Mj,and denoteybyx−1.Throughout this paper,the{ej}j∈Λand{Mj}j∈Λwill be used to indicate these net. Lemma 1wherej∈Λ and 1≤p<∞. ProofIt is well known thatLp(Mj)is the closure of Mjunder thepnorm,for 1≤p<∞.It is only needed to show thatis dense in Mjwith theLp(Mj)norm. Givenxj∈ Mjand ε>0.Let and Letxj=u|xj|be the polar decomposition ofxj,whereuis a partial isometry that can be extended to unitary in finite von Neumann algebra.Putyj=uf(|xj|).ThenUsing the continuous function calculation we can easily verify the above equation. Thus Let σ(x)be the spectral set ofx.Using the method in[3],we are finally ready to prove our Hartman Wintner spectral inclusion properties. Theorem 1Let M be a semi finite von Neumann algebra and 1 ProofIt is well known that the map L:M→B(Lp(M)):t7→Ltis isometric.So we have Since σ(Lt)⊂ σ(Tt)is equivalent to ρ(Tt)⊂ ρ(Lt),we only need to show that ifTtis bounded below then so isLt.Suppose that there exists someK>0,such that Let ε>0,0,x∈Lp(M),then there existsxj=ejxej∈Lp(Mj),such that In particular, By factorization theorem in[10],we know there exist a unitaryu∈Mjandhj∈Aj⊂Hp(M),such thatyj=hju.Then This implies that Letting ε →0,we obtain kLtxkp≥Kkxkp,i.e.Ltis bounded below.This implies that ifTtis invertible thenLtis invertible.Hence Corrollary 1Lett∈M.Thenr(t)=r(Lt)≤r(Tt).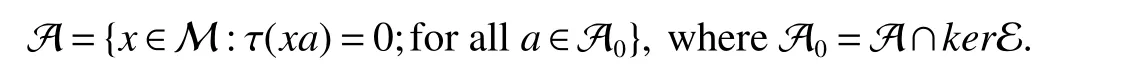
2 Hartman-Wintner spectral inclusion theorem