基于ROC的三元再编码研究

雷 蕾 王晓丹 罗 玺



基于ROC的三元再编码研究

雷 蕾①王晓丹*①罗 玺②

①(空军工程大学防空反导学院 西安 710051 )②(空军工程大学信息与导航学院 西安 710077)

针对三元编码矩阵中基分类器不包含被忽略样本类别先验知识的问题，该文提出一种基于接收机工作特性(ROC)曲线的矩阵再编码方法。首先基于ROC曲线寻找构造拒绝域的阈值对，从而获得最优分类器；然后利用最优分类器对训练样本中被忽略的类别进行分类，将经典的二值输出变为三值输出，从而对初始编码矩阵的码元“0”进行重新编码。在解码阶段，采用经典的汉明距离解码方法对未知样本进行决策。该方法能够避免基分类器的二次训练，适用于任意的三元纠错输出编码，具有良好的普适性和实用性。基于人工和UCI公共数据集的实验结果表明该方法简单高效，在不增加训练时间的基础上，能够提高解码的速度和精度，促进分类效果的提升。

三元纠错输出编码；二次编码；最优分类器；拒绝域；接收机工作特性

1 引言

纠错输出编码(Error-Correcting Output Codes, ECOC)[1]，作为一种分而治之的多类与二类分类问题的连接桥梁，已成功应用到生物学数据识别[2]、疾病诊断[3]和计算机视觉识别[4]等诸多领域。而三元纠错输出编码(ternary ECOC)[5]作为一种更为通用的ECOC类型，几乎能统一现有的所有多类分类框架。矩阵中“0”符号的引入增加了二类划分的多样性和基分类器之间的差异性，使ECOC在多类分类问题领域的性能得以提升，并已受到众多学者的关注。文献[6]讨论了一种新的编码设计准则最大化三符号编码距离准则(ternary distance)，通过该准则作者提出了一种新的稀疏编码矩阵，实验结果表明基于该准则获得的ECOC分类效果有显著提高，且与解码方法的选取相关性较小。2008年，文献[7]针对样本集线性不可分问题，提出对基类子集再分割的Subclass ECOC编码方法(SECOC)。文献[8]利用数据分布的先验知识，基于混淆矩阵和Fisher准则得到最优的子类划分，对子类采用“一对多”划分方法；在单个子类内部每次只选择两种类别作为正负类，而子类的其他类别将被忽略，即在矩阵中编码为“0”，从而弥补了单个基分类器识别的误差。文献[9]认为利用编码矩阵中二类划分的先验原始类结构信息可以提高ECOC分类性能，并给出了在流形假设和聚类假设的情况下将先验结构信息融入基分类器决策函数的方法。文献[10]针对经典的“一对一”三符号编码矩阵中码元“0”会引入分类偏差的问题，提出了避免二次训练的码元“0”再编码方法，并将该分类结果作为权值融入基于损失函数的解码过程中。文献[11]利用遗传算法来优化编码矩阵的构造，将初始ECOC编码矩阵看作遗传个体，经过交叉和变异形成新的编码矩阵。相关的研究还有文献[12-14]等，这些成果都有力地促进了三元 ECOC多类分类的发展。

在三元编码矩阵中，码元“0”所对应的类别不参与训练，因此构造得到的基分类器将不包含此类样本的先验信息。故当该基分类器作用于测试样本时，就有可能因为信息缺失而输出片面的结果，导致分类错误。本文针对此分类偏差问题，提出了一种基于ROC的再编码方法(re-coding error-correcting output codes based on ROC)。该方法能够在不进行二次训练的基础上，通过基于ROC构造的最优基分类器对码元“0”进行重新编码，使得矩阵尽可能包含所有类别样本的结构信息；同时拒绝域的构造实现了三元 ECOC对样本的选择性分类，矩阵中的“0”也在解码过程中变得更为具体，从而减小解码误差。决策时，将输出向量与新的类别编码进行Hamming距离解码。该方法采用的初始编码矩阵可以为任意的三元纠错输出编码矩阵，具有很好的普适性。

论文结构安排如下：第2节首先简要介绍基于ROC的三元再编码思想；第3节提出基于ROC再编码思想的步骤和方法，并对该方法存在的问题进行一一阐述；第4节给出实验结果和分析；最后给出总结说明。

2 再编码思想

ECOC框架中基分类器不能对样本进行选择性分类，而对于未参与基分类器训练的样本而言，直接对其分类将引入误差。

问题1 假设有符合高斯混合分布的5类数据(ecoli数据集1))，如图1所示。当采用“一对一”方法对其进行编码时，由和作为训练样本产生的基分类器的决策面也能在一定程度上对类别,和进行正确的划分。这样，基分类器就能在测试时对其做出正确的硬判决输出。针对此问题，文献[10]提出了一种不需要重新训练的再编码方法，通过已训练的基分类器对码元“0”所对应的类别进行分类，通过设定分类正确率的阈值，将其重新编码为{1, -1}。但对于编码矩阵中遗留的码元“0”仍采用传统的损失函数进行解码。

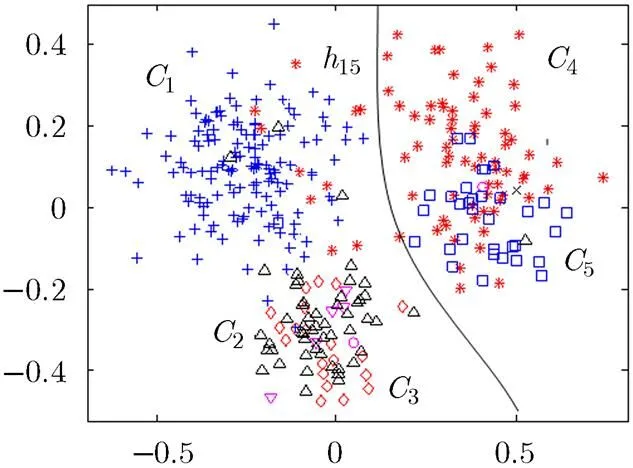
图1 5类数据集分布

从图2中可以看出，根据Hamming距离解码和欧式距离解码，未知样本被判定为。但事实上属于第2类。因为只有当类在基分类器训练中没有被忽略时，其类别属性与类一致；当类被忽略时基分类器的决策面不能对样本进行正确识别。出现这样的情况是由于编码矩阵中码元“0”的干扰，使训练得到的分类器不包含对应类别的分布信息，在解码过程中引入了偏差，从而不能做出正确的判决。本文结合问题1和问题2，将“拒绝域”引入每一个基分类器，对样本输出值落入拒绝域中的样本予以拒绝，不对其进行分类识别，使基分类器的输出由二元值扩展到三元值，从而减少基分类器对“0”标识的类别样本直接分类带来的误差。具体来讲：就是用训练好的基分类器对码元‘0’所对应的样本进行分类，根据一定的拒绝域准则，将“0”重新编码为“1”或“-1”；如果码元“0”所对应样本的输出落入拒绝域，此时选择性拒判就产生了，此类别在新的编码矩阵中码元依旧为“0”，这样就从本质上减小了利用Hamming距离解码时带来的误差，从而克服了问题2。

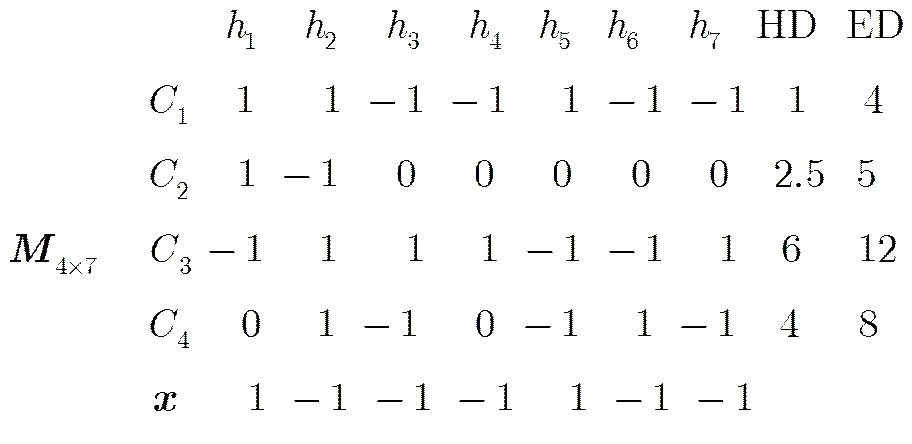
图2 编码矩阵

要实现选择性拒判，关键是构造拒绝域。作为分类器性能评估的有效手段，ROC曲线判决直观、概念清楚，对样本数据的先验分布知识和错分代价矩阵都不敏感，为解决前面提到的拒绝判决问题提供了强大的工具。为此本文引入ROC来设计拒绝域，构造最优分类器进行再编码设计。根据以上分析，图3给出了基于ROC的三元再编码的多类分类结构框图。其中和分别代表训练样本的训练子集和验证子集。值得注意的是，再编码过程仍然在样本训练阶段进行，这样就避免了二次训练，减少了训练时间。

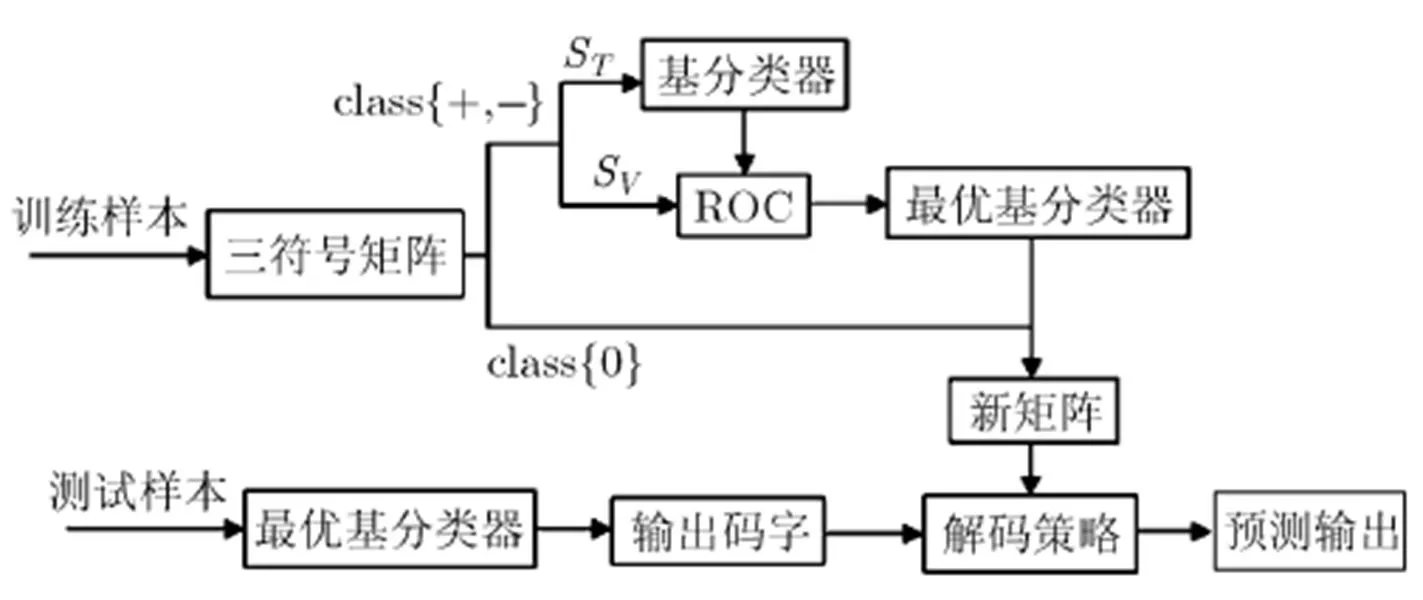
图 3 基于ROC的三元再编码多类分类结构框图

3 基于ROC的三元再编码研究方法

本节利用ROC构造阈值对，进而得到带拒绝域的最优分类器，通过其对训练阶段所忽略的类别样本进行分类再编码，最终得到新的编码矩阵。

3.1基于ROC的最优分类器

为了说明ROC的生成及相关特性，首先简要介绍两类样本混淆矩阵的相关概念。混淆矩阵描绘了样本数据的真实类别属性与识别结果之间的关系，是评价分类器性能的一种常用的有效方法。假定一个二分器的分类结果为一个的混淆矩阵，如表1所示，其中行元素代表样本的真实属性，列元素代表分类器的分类结果。矩阵中：TP为正确分类的正类样本数；FP为被错误分类的负类样本数；FN为被错误分类的正类样本数；TN为正确分类的负类样本数。定义代价矩阵，其中TP和TN的分类代价为0。为代价矩阵的费效比(cost ratio)。由此定义该分类器的分类损失代价为

表1混淆矩阵和代价矩阵

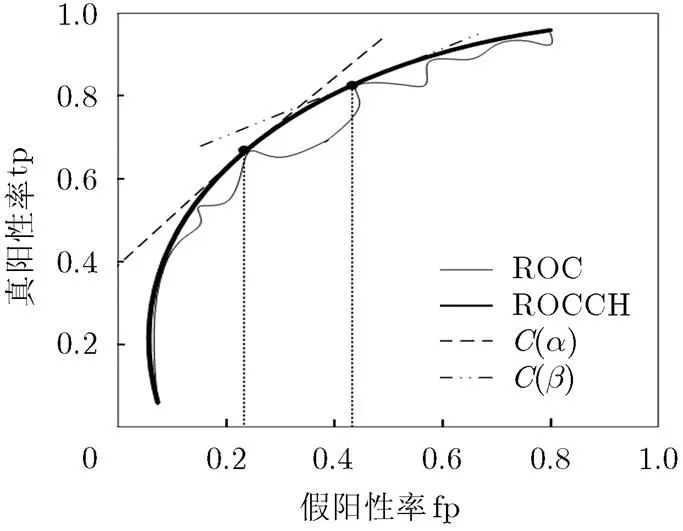
图4 ROC曲线特性

令式(4)等于0得到最终结果为

由式(5)就可获得ROC曲线上满足要求的两点，以此作为该基分类器产生拒绝域的阈值对。由前面的假设可知,。由于ROC的凸包是递增和凸的，所以它的一阶导数是非负和非增的，也就是。所以代价矩阵需要满足以下条件：

3.2新编码矩阵的生成

上一节通过ROC曲线构造出带拒绝域的基分类器并获得阈值对。其再编码过程为

表2基于ROC三元再编码的多类分类方法

下面将重点通过实验验证该方法所得的编码矩阵在分类中的应用效果。

4 实验

本节采用人工数据集和UCI数据集来验证本文方法的分类效果。

4.1实验数据

实验中所用的第1类数据集为5类2维正态分布人工数据集[16]，各类别数据的先验概率相同且样本个数为400，其类别分布参数如表3所示。

表3 5类人工数据集各类别分布参数

第2类数据集为UCI数据集，其各类数据描述如表4所示，针对部分UCI数据集，本文对其进行了归一化处理，并删除了一些样本数很小的类，同时为了提高分类速度，实验中对高维数据使用主成分分析法(PCA)进行了降维处理。

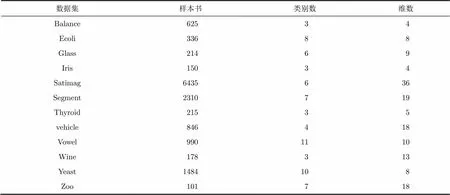
表4 UCI数据集及数据描述

4.2实验设计

实验比较了原始“一对一”编码、稀疏随机编码和基于两者的再编码矩阵的分类效果。在选择随机编码方法时，我们将分别从已产生的2000个稀疏随机编码阵集(对应各码元,,)中随机选择所需要的编码阵。基分类器采用了线性逻辑分类器(LOGLC)和多项式核函数支持向量机()。采用Hamming距离进行解码，输出最后分类决策。

在估计分类错误率时为保证估计的准确性，样本数据个数大于500时我们采用10重交叉验证，小于500时采用5重交叉验证，双边估计t检验法见文献[17]。

ROC曲线的绘制采用算法2实现[18]，如图5所示，其中,分别为正负样本个数。根据3.1节的方法求出该基分类器对应的阈值对和最优分类器，用于下一步测试样本的分类。

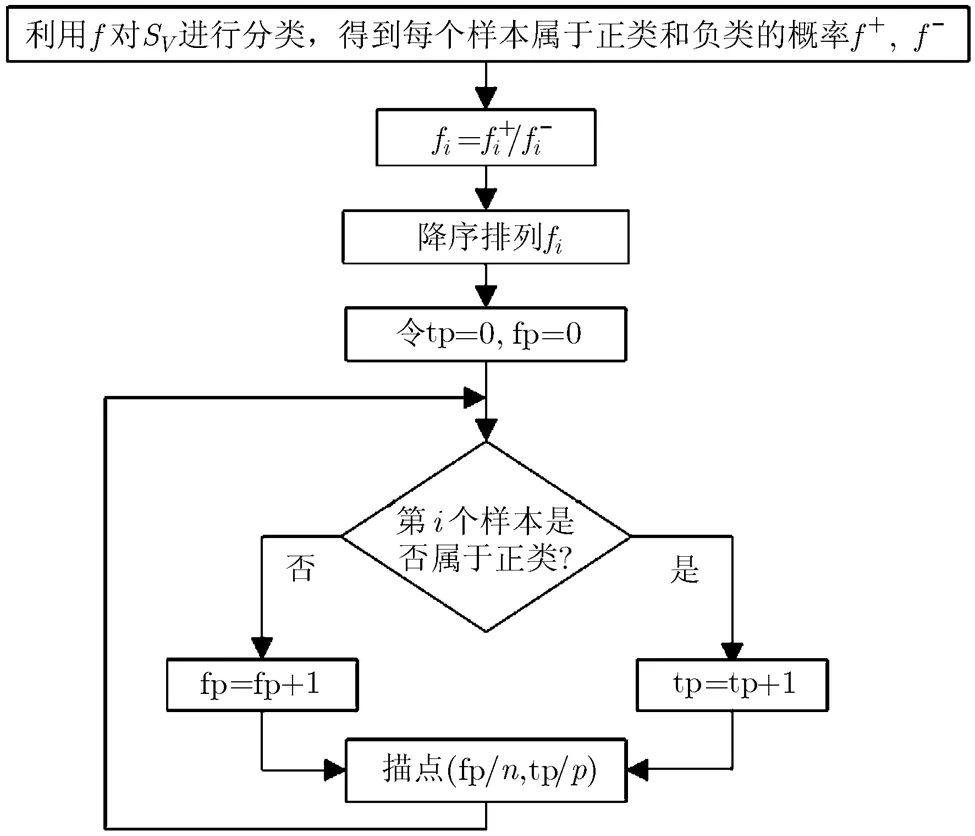
图5 ROC曲线的实现

4.3 实验结果及分析

4.3.1人工数据集 图6展示了基于一对一编码矩阵的线性逻辑基分类器所绘制的ROC曲线。从图6中可以看出，将所有的点根据不同的决策阈值进行分类，得到一条从点(0,0)向点(1,1)方向延伸的ROC曲线，并最终趋于稳定。而对于有限数据集合而言，生成的ROC曲线是阶梯形状的，只有当样本数据趋近无穷时，才能得到理论上的真实ROC曲线。

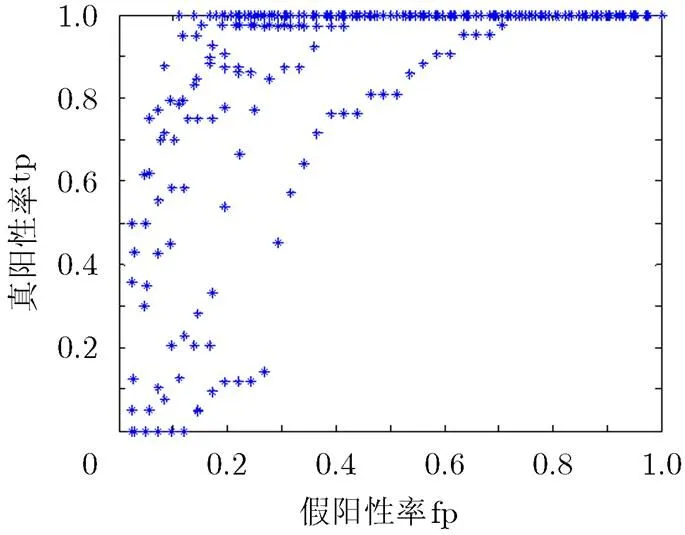
图6 ROC实验曲线

对于人工数据集而言，正负类样本比例大致为1 : 1，所以得到的最优分类器的阈值为，表5为验证集的分类正确率。其中为基分类器，为类别。

表5基于验证集的分类正确率

得到新的编码矩阵如表6所示。

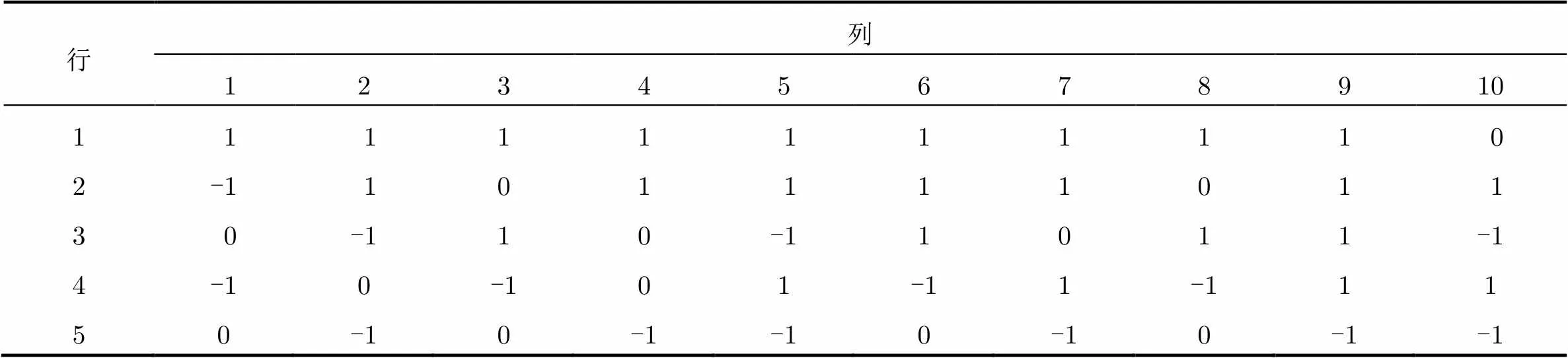
表6新编码矩阵行列

表7所示结果为各编码类型在人工数据集下的分类正确率及其置信区间。ROC+编码方法为对应的基于ROC的再编码多类分类方法。

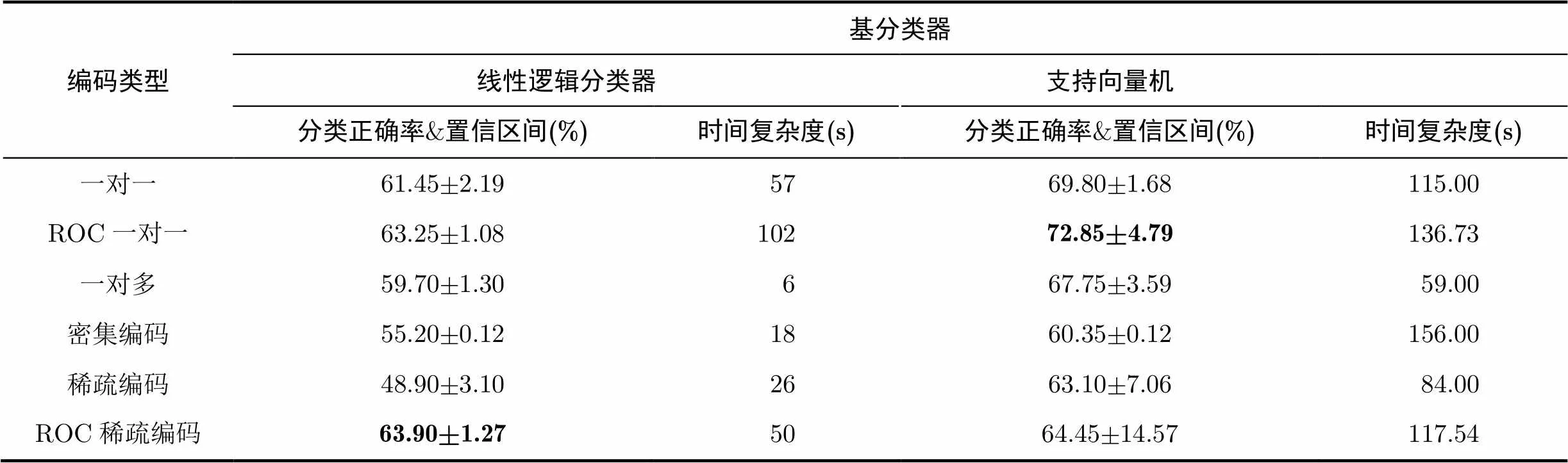
表7人工数据集分类正确率及置信水平为0.95的置信区间(%)

从表7可以看出，基于ROC的再编码方法是有效的，其分类得到的结果要优于原始编码方法，而基于一对一编码方法分类精度的提高要高于随机编码，这是因为在一对一编码中，码元“0”所占的比例高，对其进行再编码，能明显地减少“0”的数量，缩小测试样本输出向量与真实类码字的距离，从而提高分类正确率。同时再编码的复杂度也没有明显的增加，所需时间消耗在可接受范围内。

4.3.2 UCI数据集 表8和表9列出了分别以SVM和LOGLC作为基分类器的不同编码方法的分类结果比较。其中Re-为文献[10]所采用的再编码方法。在每张表中加粗的数据为最大分类正确率。

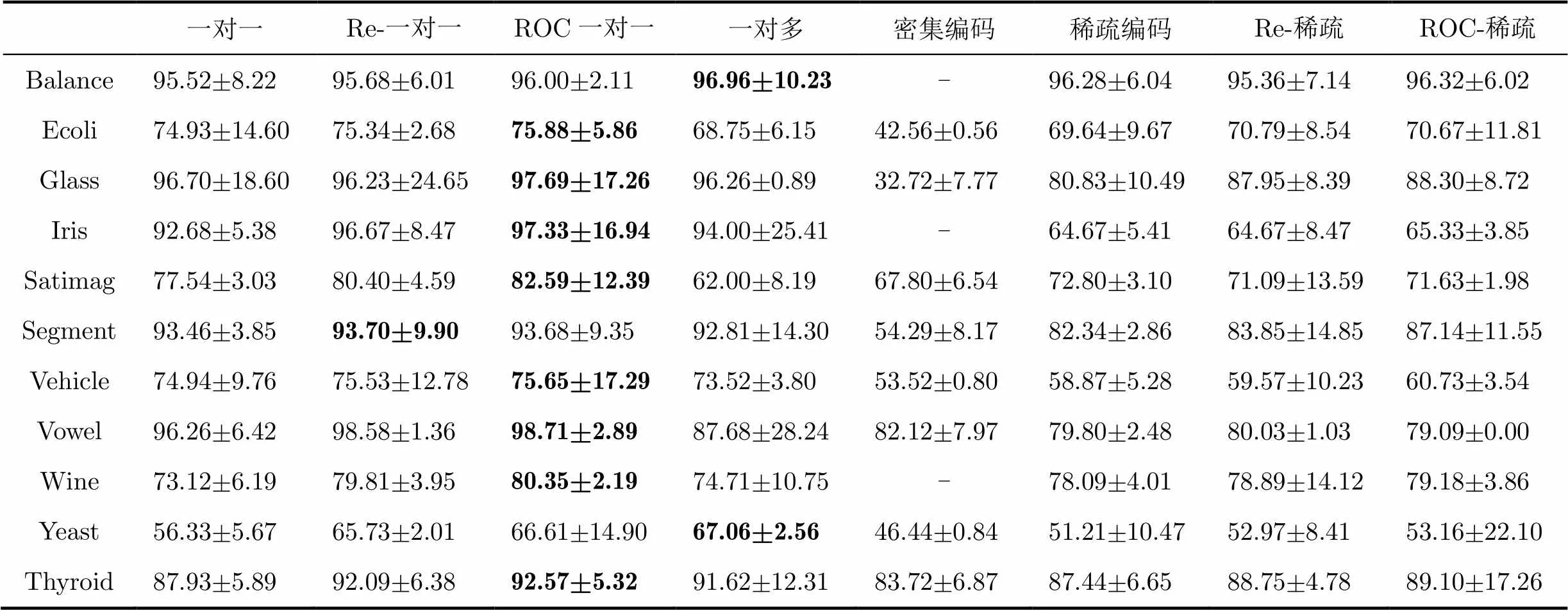
表8基于SVM和Hamming距离解码的各数据集分类正确率及置信水平为0.95的置信区间(%)

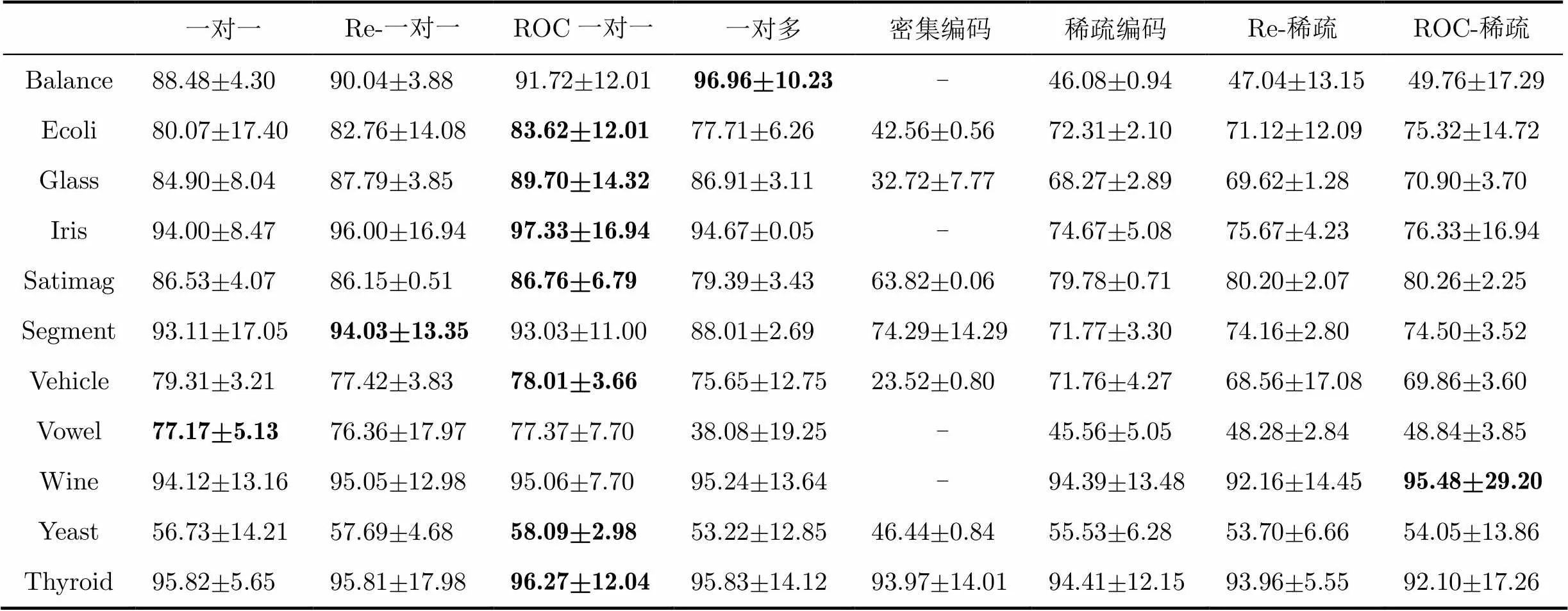
表9基于LOGLC和Hamming距离解码的各数据集分类正确率及置信水平为0.95的置信区间(%)

从实验结果可以看出，基于ROC的再编码方法在大部分数据集上能获得较好的分类效果。尽管Re-ECOC有时能取得更好的分类效果，但它不能实现基分类器的选择性分类，对一些错分代价较大的样本有一定的局限性。同时基于“一对一”编码矩阵的ECOC多类分类方法在大部分数据集上的分类性能提升优于基于随机编码的ECOC分类。而对于Glass数据集而言，基于稀疏随机编码提高的幅度较大，这是因为此时稀疏编码矩阵为

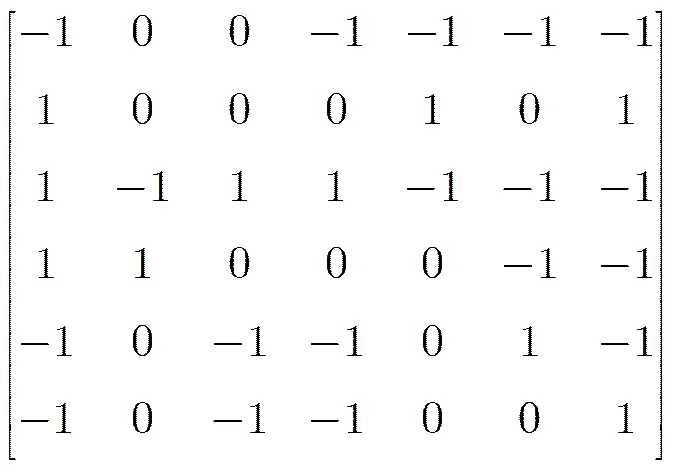
可以看出，此时的编码矩阵中“0”的数量较多，对其采取再编码策略能够明显地提高分类性能。

为了更直观地体现再编码对码元“0”的影响，本文引入拒分率来对编码前后的分类性能进行比较。

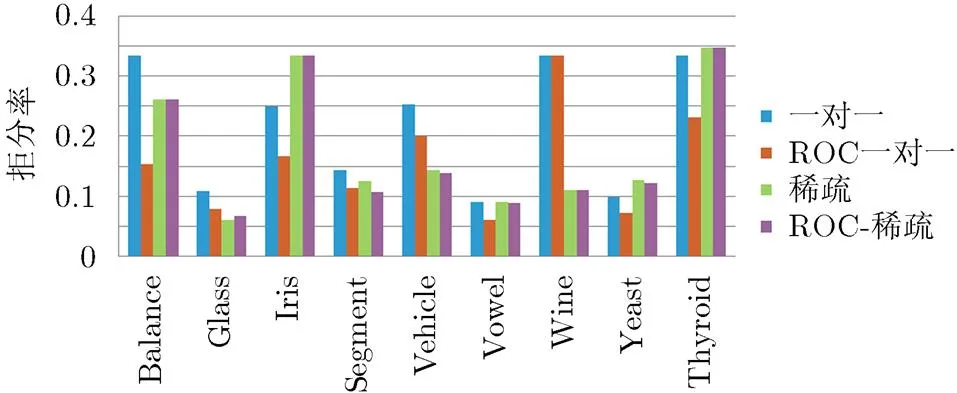
图7 拒分率比较

5 结束语

在三符号ECOC多类分类中，码元“0”对应的类别样本将不参与此列基分类器的训练，因此利用该基分类器对未参与训练的类别样本进行分类可能会带来误差。本文提出的再编码 ECOC方法在不进行二次训练的前提下，通过引入“拒绝域”来实现选择性分类，将基分类器的二值输出扩展为三值输出，从而实现编码矩阵中的码元“0”再编码，缩小预测输出与类别码字的距离，提高分类正确率。在为基分类器构造拒绝域时，一种基于ROC曲线的拒绝域构造方法被应用到再编码过程中。最后实验验证了本文方法的有效性。本文为实现多类别的选择性分类提供了新思路。如何从降低误判风险出发，研究有效的带拒绝域的ECOC多类分类方法是下一步的工作重点。

参考文献

[1] DIETTERICH T G and BAKIRI G. Solving multi-class learning problems via error-correcting output codes[J]., 1995, 34(2): 263-286. doi: 10.1613/jair.105.

[2] PHYO K S, JIAN G W, and EAM K T. Facial age range estimation with extreme learning machines[J]., 2015, 149A: 364-372. doi: 10.1016/ j.neucom.2014.03.074.

[3] ELIF D Ü. ECG beats classification using multiclass support vector machines with error correcting output codes[J]., 2007, 45(17): 675-684. doi: 10.1016/j.dsp. 2006.11.009.

[4] SERGIO E, DAVID M, ELOI P,. Online error correcting output codes[J]., 2011, 32(3): 458-467. doi: 10.1016/j.patrec.2010.11.005.

[5] ERIN L A, ROBERT E S, YORAM S,. Reducing multiclass to binary: a unifying approach for margin classifiers[J]., 2000, 39(1): 113-141. doi: 10.1162/15324430152733133.

[6] SERGIO E, ORIOL P, and PETIA R. Separability of ternary error-correcting output codes[J]., 2009, 30(5): 285-297. doi: 10.1016/j.patrec.2008.10.002.

[7] SERGIO E, DAVID M J T, ORIOL P,. Subclass problem-dependent design for error-correcting output codes [J]., 2008, 30(6): 1041-1054. doi: 10.1109/TPAMI. 2008.38.

[8] 周进登, 王晓丹, 周红健. 基于混淆矩阵的自适应纠错输出编码多类分类方法[J].系统工程与电子技术, 2012, 34(7): 220-226. doi: 10.3969/j.issn.1001-506X.2012.07.38.

ZHOU Jindeng, WANG Xiaodan, and ZHOU Hongjian. Multiclass classification of adaptive error-correcting output codes based on confusion matrix[J]., 2012, 34(7): 220-226. doi: 10.3969/j.issn. 1001-506X.2012.07.38.

[9] WANG Y, CHEN S C, and XUE H. Can under-exploited structure of original-classes help ECOC-based multi-class classification?[J]., 2012, 89: 158-167. doi: 10.1016/j.neucom.2012.02.035.

[10] SERGIO E, ORIOL P, and PETIA R. Re-coding ECOCs without Re-training[J]., 2010, 31(7): 555-562. doi: 10.1016/j.patrec.2009.12.002.

[11] MIGUEL A B, SERGIO E, XAVIER B,. On the design of an ECOC-compliant genetic algorithm[J]., 2014, 47(2): 865-884. doi: 10.1016/j.patcog. 2013.06.019.

[12] FRANCESCO C, ORIOL P, and PETIA R. ECOC-DRF: discriminative random fields based on error correcting output codes[J]., 2014, 47(6): 2193-2204. doi: 10.1016/j.patcog.2013.12.007.

[13] MIKEL G, ALBERTO F, EDURNE B,. DRCW-OVO: distance-based relative competence weighting combination for one-vs-one strategy in multi-class problems[J]., 2015, 48(1): 28-52. doi: 10.1016/j.patcog. 2014.07.023.

[14] LEI L, WANG X D, LUO X,. Hierarchical error-correcting output codes based on SVDD[J]., 19(1): 163-171. doi: 10.1007/ s10044-015-0455-5.

[15] TADEUSZ P. On the use of ROC analysis for the optimization of abstaining classifiers[J]., 2007, 68(2): 137-169. doi: 10.1007/s10994-007-5013-y.

[16] ZHOU J D, and WANG X D. Research on the unbiased probability estimation of error-correcting output coding[J]., 2011, 44(7): 1552-1565. doi: 10.1016/ j.patcog.2010.12.020.

[17] ZHOU J D, YUN Y，ZHANG J M,Constructing ECOC based on confusion matrix for multiclass learning problems[J]., 2016, 59(1): 1-14. doi: 10.10071/s11432-015-5321-y.

[18] 邹洪侠, 秦峰. 二类分类器的ROC曲线生成算法[J]. 计算机技术与发展, 2009, 19(6): 109-112.

ZOU Hongxia and QIN Feng, Algorithm for generating ROC curve of two-classifier[J]., 2009, 19(6): 109-112.

Recoding Error-correcting Output Codes Based on Receiver Operating Characteristics

LEI Lei①WAGN Xiaodan①LUO Xi②

①(,,’710051,)②(,,’710077,)

As to the problem that the base classifiers in ternary Error Correcting Output Codes (ECOC) matrix do not contain the prior information of classes which are ignored in binary splits, a new recoding ECOC based on Receiver Operating Characteristic (ROC) curve is presented. To recode the ternary matrix, the two thresholds of reject region are obtained based on ROC to build the optimal classifiers. Then, the optimal classifiers are used to classify the ignored classes based on bipartition in training phase. In so doing, the classical two-symbol output expands to three-symbol to recode the zeros. Finally, the Hamming decoding strategy is adopted for decision in decoding. This method can avoid a second training and is applied to any kind of ternary matrix. The experiments based on Synthetic and UCI datasets validate the better efficiency and remarkable promotion without increasing training complexity of the proposed approach.

Ternary error-correcting output codes; Recoding; Optimal classifier; Reject option; Receiver Operating Characteristics (ROC)

TP391

A

1009-5896(2016)10-2515-08

10.11999/JEIT151343

2015-12-01；改回日期：2016-06-06；网络出版：2016-08-26

王晓丹 afeu-wang@163.com

国家自然科学基金(61273275, 61503407)

The National Natural Science Foundation of China (61273275, 61503407)

雷 蕾： 女，1988年生，博士生，研究方向为机器学习、多类分类.

王晓丹： 女，1966年生，教授，博士生导师，研究方向为机器学习、计算机视觉处理、信息融合.

罗 玺： 男，1988年生，硕士，讲师，研究方向为智能信息处理.

1)对ecoli数据集进行了归一化处理，并删除了一些样本数很小的类