提高学生参与数学课堂的策略探究
——以“五环导学”试验为例
陈联沁 陈桂芬
(1.尤溪第一中学,福建 尤溪 365100;2.三明市第九中学,福建 三明 365000)
提高学生参与数学课堂的策略探究
——以“五环导学”试验为例
陈联沁1陈桂芬2
(1.尤溪第一中学,福建 尤溪 365100;2.三明市第九中学,福建 三明 365000)
“五环导学”课改试验总结了一些提高学生课堂效率的办法,利用信息技术多媒体功能激发学生兴趣,吸引学生主动参与;通过给学生足够的时间、空间,信任学生,鼓励学生大胆参与;再教给学生探究方法,引导学生深层次参与等办法来提高教学效率。
五环导学;探究;参与
在“互联网+”影响的大数据环境下,国内外再次兴起大规模课改,例如,国外推行的“翻转课堂”“慕课”等等。笔者结合学生实际进行新的教育方式探究“五环导学”试验——即自主、合作、探究、检测、反馈。以下笔者就如何提高学生的课堂参与度,[1]提高教学课堂效率谈几点自己的看法:
一、利用信息技术激发学生兴趣,吸引学生主动参与
如果学生对学习内容发生兴趣,他就会积极主动、心情愉悦地进行学习,这时学习不再是一种负担,此时的学习不仅是主动,而且可以深入参与。在笔者的“五环导学”试验中,学生的自主学习,主动参与是首要的一个环节,而多媒体对于激起学生兴趣十分有帮助。
试验案例1:课堂引入:用幻灯片展示一根圆柱
师:用一个平面去截这根圆柱,截面会是怎样的呢?
生:圆。(异口同声)
师:你是怎么截的,有其他形状吗?若截面与转轴不垂直呢?
(学生们进行想象、比划、探讨)1分钟后
生:矩形,还有两个图形不好说,另两边是弧形。
教师利用多媒体功能,在不同方向用一个平面去截这根圆柱,并将截面向外展示出来,教师告诉同学们其中那个比圆更瘪的图形就是今天要学习的椭圆。这精美、直观的图形一下吸引了学生的注意力,先给了学生一个椭圆大致的印象。
接着教师让学生按课本2-1的2.2.1的探究步骤进行操作:取一根定长的绳子,并将绳子两端分别固定在本子的两点上,套上铅笔,拉紧绳子,并移动尖。
教师引导学生操作,并用几何画板模拟实验,注重知识的生成过程,[2]最后展示学生作品,学生的注意力一下就被吸引住了,学生的积极性也被调动起来,数学课也可以和其他科的课一样活跃起来,学生主动参与就不再是问题。
二、给学生足够的时间、空间,鼓励学生大胆参与
对学生持鼓励、信任的态度有利于学生参与,“五环导学”试验要求充分信任学生,以讲评课为例,试验中教师放手给学生,让学生当“小教师”,通过“合作”来完成,即自己来批改、发现问题并进行订正,变式巩固,给足时间让学生领悟知识的易错点[3],关键点。
试验案例2:教师将学生的作业通过投影再现在黑板上,让所有的同学看到他们书写的结果,并让学生们自己来批改、订正。具体步骤如下:
(一)将学生做的作业(原稿)投影在黑板上。在四棱锥P-ABCD中,侧面PCD⊥底面ABCD,PD⊥CD,底面ABCD是直角梯形,AB∥CD,∠ADC=90°,AB= AD=PD=1,CD=2.
(Ⅰ)求证:BC⊥平面PBD;
(Ⅱ)求直线AP与平面所成角的正弦值;
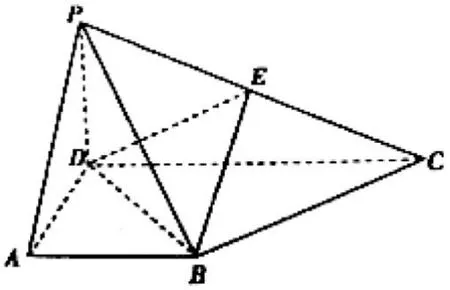
学生解答:
错解1.

纠错:
错解2.
∵侧面PCD⊥底面ABCD,
∵PD∈面PCD,BC∈面ABCD,
∴PD⊥BC.
纠错:
This treatise is a summary of the philosophical views of the Mahāyānist Madhyamaka School, it is a work of significant academic value.
(二)由学生来批改、找错误;
(三)由学生来总结错误的原因、从而达到认识错误,必要时教师进行引导、点拨;
(四)提问立几中还有哪些知识点是本题没考到的?由学生思考出题变式。
这种习题课形式新颖,气氛活跃,学生从听教师讲的被动学习转变为自己讲,大家一起改作业,寻找别人错误的同时对照自己的错误、改正错误、并认识错误的根源;并把这一板块的知识进行系统复习,梳理,实现知识重组与迁移[4],实现了自觉参与课堂。
三、教给学生探究方法,引导学生深层次参与
创新意识和创新能力的培养是素质教育的核心内容,“五环导学”试验强调合作、探究,试验的探究课改变了传统的探究课上法,在试验中教师主要是教会学生探究的方法、及如何进行、确定探究方向,而具体的探究的过程、及验证探究所得的规律都由学生自己进行,最后,教师和学生一起检验,反馈所得的结果。
试验案例3:一位专家的课,课题是:数学实验——探究圆锥曲线中一类定值问题。[5](这次上课的班级人手配备一个TI图形计算器)步骤如下:
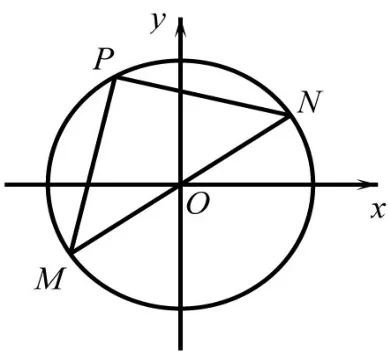
(一)教师讲授研究数学的方法——数学实验法,讲述实验法的基本步骤,紧接着结合本节课内容抛出问题,引中建构数学实验的基本步骤。
(二)教师以层层递进的方式设置了以下四个问题,引导学生探究,让学生动手操作在中实践学习数学实验的基本方法:
(教师用几何画板展示图形)
生:∠MPN=90°,PM2+PN2=MN2,kPM·kPN=-1,
师:若将圆换为椭圆,那还会有这些性质吗?
教师让学生拿出TI图形计算器,进行实验,寻找其中的规律,教师进行相应的引导:
1.圆→椭圆,直径→?(长轴,还是短轴)弦→椭圆中的什么线?这些线又具有什么特点?
2.点P在椭圆上动,有哪些不变的性质?
(实验进行5分钟后)
学生进行试验发现斜率积不变,教师进行演示实验。
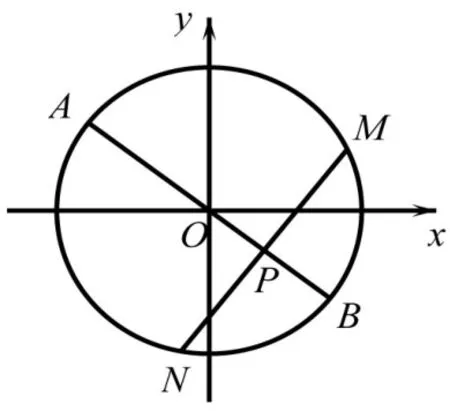
任一点,当kPM,kPN都存在时,证明:
(三)在交流分享中确认数学实验的基本模式。在本节课中,教师给学生留下的不只是学生探究出来的几个结论,更多的是数学独特的思维方式、解决问题的方法。多年后,学生也许会忘掉教师所教的数学知识,但他们的脑海里一定还积淀着数学的逻辑分析问题、解决问题的思维能力。让学生充分的进行自主探究,深层次参与培养的是学生的能力,留下更多与素质相关的东西。
总之,要提高教学效率,关键在于最大限度地调动学生参与,这也恰恰是建构主义学习理论要求的。学习是学生主动建构的过程,不是教师向学生传递的灌输的过程,而是学生通过学习对新旧知识、经验的再认识、内化、升华构建新的认知体系[6],是学生主动参与的过程。让学生亲自参与研究,学会学习,激发学生的创造性思维,这才是素质教育的真正意义所在。
[1]章建跃.什么是好数学教学[J].中小学数学(高中版),2011(02).
[2]章建跃.注重课堂生成才是好数学教学[J].中小学数学(高中版),2011(12).
[3]章建跃.数学课改需要有平常心[J].中小学数学(高中版),2015(03).
[4]涂荣豹.数学学习与数学迁移[J].数学教育学报,2006(11).
[5]张佳,黄炳锋.融合手持技术的探究式学习的实践与思考——以《探究圆锥曲线中一类定值问题》为例[J].数学通报,2015(10).
[6]涂荣豹,喻平.建构主义观下的数学教学论[J].南京师大学报,2001(03).
G420
A
1673-9884(2016)05-0062-03
2016-04-20
陈联沁(1980-),男,福建尤溪人,尤溪第一中学中级教师。

