基于反激变换器的电池均衡系统双闭环控制器仿真设计

万明，江学焕，贾蓉，简炜

（湖北汽车工业学院电气与信息工程学院，湖北十堰442002）

基于反激变换器的电池均衡系统双闭环控制器仿真设计

万明，江学焕，贾蓉，简炜

（湖北汽车工业学院电气与信息工程学院，湖北十堰442002）

设计了一种基于反激变换器的电池均衡系统双闭环控制器。首先分析了反激变换器的工作模式，然后采用开关器件平均模型法建立了小信号模型，在此基础上设计了电流内环和电压外环的PI调节器参数。最后在Matlab/Simulink环境下搭建了双闭环控制系统的仿真模型，通过对比论证，验证了该方法具有一定的优越性。

反激变换器；电池均衡；双闭环控制

当前，动力电池技术还不够成熟，而且成本较高是制约电动汽车发展的主要因素［1］。锂电池是目前最具发展潜力的汽车动力电池，但是锂电池在成组使用时存在着不一致性的问题，影响了电池组的使用寿命和安全性，必须采用电池均衡系统来实现能量的均衡管理［2-3］。能量耗散型均衡系统由于浪费能量而且带来热量管理等问题已经逐渐被淘汰；能量非耗散型均衡是未来发展趋势，基于不同的储能装置可分为电容均衡器、电感均衡器和变压器均衡器等。反激式变换器具有均衡速度快、传递效率高等优点，但是存在着电流可控性差的问题［4］，此外电池在充放电工作时对均衡系统的稳定性产生扰动。针对反激式变换器均衡的这些特点，设计了一种基于反激式变换器均衡系统的双闭环控制器。这种双闭环控制器包括电流内环和电压外环，采用经典控制理论中的反馈调节和PID调节的控制方法，具有较好的稳定性，动态性和抗干扰能力。本文中首先用开关元件平均模型法对反激变换器建模，在小信号模型分析的基础上设计双闭环控制系统，使变换器能随外部扰动自动改变占空比来调节变换器的输出电压，并使其稳定在恒定值。最后在Matlab/Simulink环境中搭建了双闭环控制系统的仿真模型，并且加入了干扰环节来进一步验证控制系统的正确性和抗干扰能力。

1　工作原理

反激变换器均衡系统结构框图如图1所示，通过相应均衡控制策略控制反激变换器工作，实现能量从电池单体中转移到自身或其他的电池组中，从而使各电池组中各电池单体能量保持均衡。

图1　反激变换器均衡系统框图

该均衡系统的核心是反激变换器，其电路拓扑结构如图2所示。由于变换器中励磁电感参与了能量传递，因此可以将反激变压器等效为由一次侧的励磁电感L与匝比为1：n的理想变压器相并联的模型来替代［5］。

图2　反激变换器电路拓扑结构

根据变压器的电流是否连续，可将其工作模式［6］分为连续导电模式（CCM）和不连续导电模式（DCM），在不考虑变压器的漏感和其他损耗时得到CCM模式下理想反激变换器的2种工作状态，如图3所示。当开关管Q导通时，变压器初级侧接入直流电源，变压器的励磁电感L产生感应电动势，而次级侧由于二极管D承受反向电压处于截止状态，此时变压器存储能量，滤波电容向负载供电。当开关管Q断开时，次级侧产生的感应电动势反向，二极管导通，此时变压器释放能量并给电容和负载供电。

图3　理想反激变换器2种工作状态

2　理想反激变换器建模

分析图3所示反激变换器的2种工作状态，可知

则在一个周期Ts内ig（t）与vD（t）的平均变量为

图4　理想反激变换器平均变量等效电路

对图4进行等效变换，各平均变量等于其对应的直流分量、电感短路、电容开路，得到如图5a所示的理想反激变换器直流等效电路。分析图5a有：

由式（5）得到理想反激变换器在静态工作点：

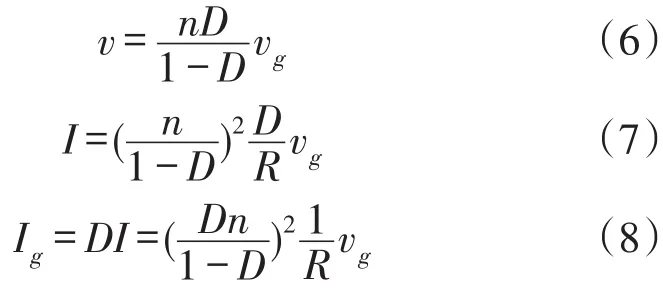
将图4中各平均变量分解为相应的直流分量与交流小信号分量之和，忽略小信号分量的乘积项和直流项，将平均等效电路中的受控电流源用并联的受控电流源与独立电流源来代替；将受控电压源用串联的受控电压源与独立电压源来代替，得到理想反激变换器的交流小信号等效电路，如图5 b所示，各变量均表示为s域形式。分析图5 b，由电感和电容的特性有：

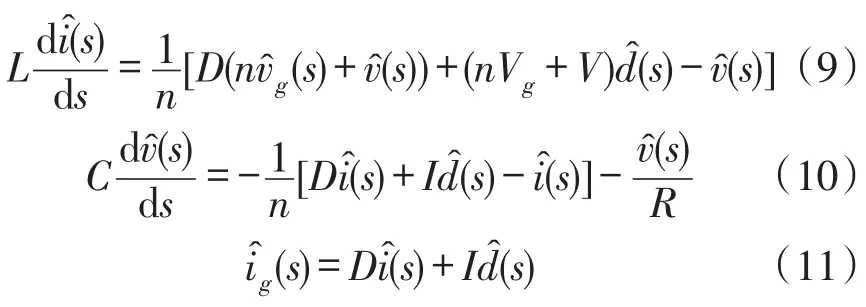
得到反激变换器控制——输出电压的传递函数：

对于一个SST而言，SST回波间隔距离会小于或等于多帧积累时间内的SST运动距离，根据多帧积累时间和SST运动速度得到SST运动的距离门限，通过距离门限检测出可能的SST。

图5　理想反激变换器等效电路

变换器控制——初级侧电感电流的传递函数：

3　双闭环控制系统设计

利用开关元件平均模型法对变换器进行建模和小信号分析，得到变换器的传递函数。由此可以分析系统的开环幅频特性，并根据系统频域指标分别设计电流环和电压环的PI调节参数，使变换器的输出电压能够抗干扰并稳定在所需求的电池充电电压范围内。

该双闭环控制系统的控制框图如图6所示，控制思想是：将基准电压与输出电压的采样值相减得到电压误差信号，再经过电压环PI调节器补偿环节Gvc（s）构成电压外环；将电压环的输出作为电流内环的基准输入，其与电感电流的差值经过电流环PI调节Gic（s）后作为电感电流对占空比控制信号的输入，由此构成电流内环。最终通过控制PWM波的占空比来调节输出电压值。

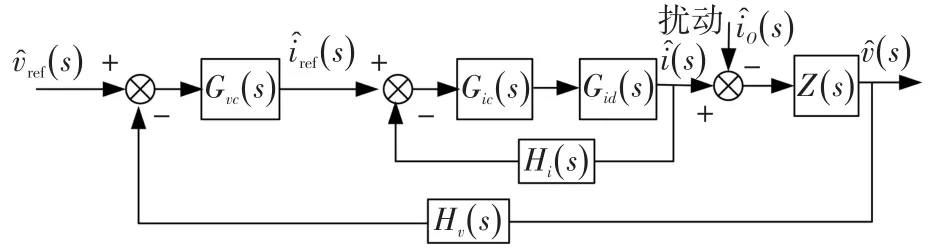
图6　双闭环控制系统控制框图

3.1设计需求

输入电压为单节锂电池的工作电压，其工作范围一般为2～4V，这里取Vg为2V；输出电压为一组电池电压V为24V，变压器匝比n为15，变压器励磁电感L为10μH，电容C为470μF，负载电阻R为1 Ω，开关频率fs为50 kHz。

3.2电流内环的设计

电流内环的设计主要是设计合理的PI调节器参数，使得内环输出满足系统的稳定和响应特性。电流内环的设计主要是设计PI调节器的参数，使得电流内环的输出满足系统的稳定及响应特性。将设计参数代入式（6）～（8）和式（13）中，得到占空比对输入电流的传递函数：

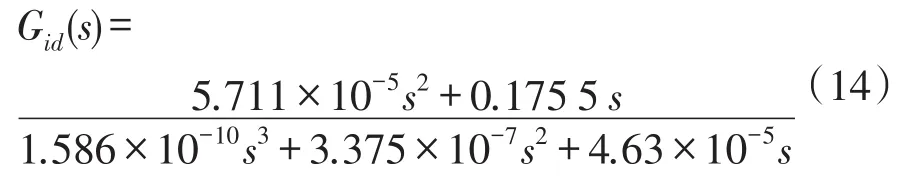
根据式（14）得到电流内环在添加PI补偿环节前的开环幅频特性，如图7中曲线Gil（s）所示。同时，可以得到系统截止频率wc为3.57×105rad·s-1，超出了变换器的开关频率（3.14×105rad·s-1），而且高频段衰减较慢，因此需要添加PI补偿。假设内环PI调节器Gic（s）=Kp1+Ki1s，利用Matlab的自整定功能，选取PI调节参数Kp1为0.106，Ki1为71.32。经过PI补偿后的系统内环幅频特性如曲线Gcc（s）所示，系统的截止频率变为3.84×104rad·s-1，相角裕度γ为87.6°，系统动态性和稳定性满足要求。电流内环开环传递函数为

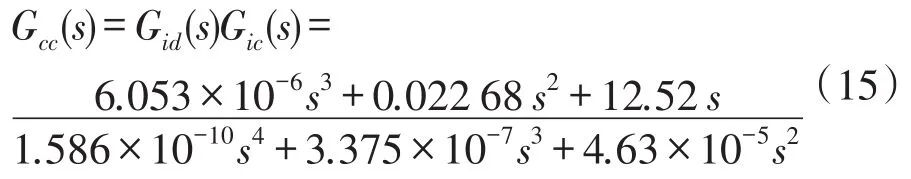
3.3电压外环的设计

将设计好的电流内环闭环传递函数与负载传递函数相串联，作为电压外环的一个环节，根据此传递函数确定电压外环的PI调节参数。负载传递函数为

则电压外环加补偿前的开环传递函数为

加入补偿前的外环幅频特性如图7中曲线Gvo（s）所示。假设电压外环PI调节器Gvc（s）=Kp2+Ki2s，经过Matlab自整定可以得到电压外环的PI调节器参数Kp2为0.99，Ki2为2290，即电压外环的PI环节传递函数为

添加外环PI补偿后，可以得到整个双闭环控制系统的幅频特性如图7中曲线Go（s）所示，从图中可以看出：系统在低频段的直流增益很大，表明系统的稳态误差较小，系统在截止频率2232 rad·s-1处的相角裕度γ为86°，表明系统的动态稳定性较好、抗干扰能力强。

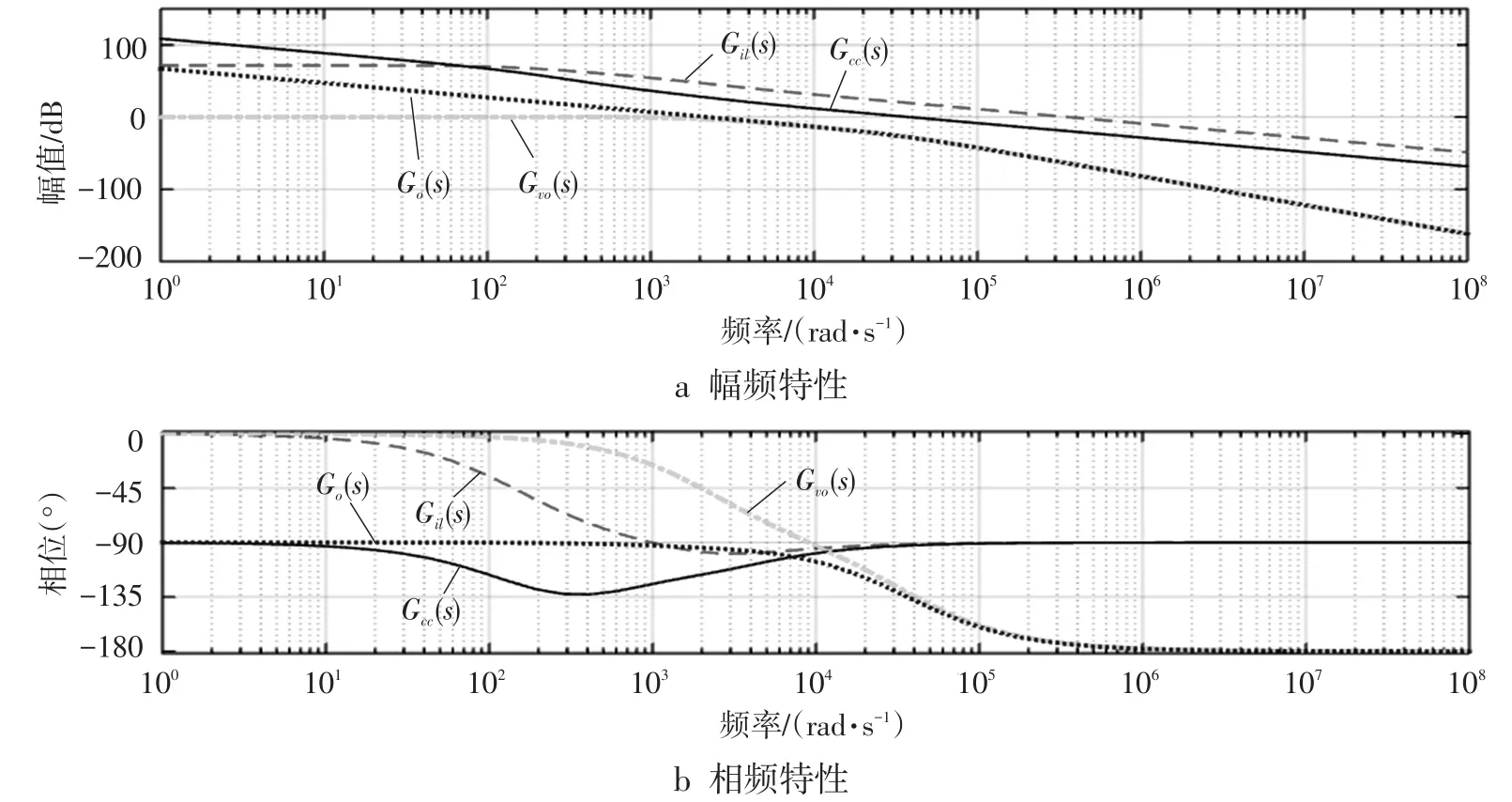
图7　系统伯德图

4　仿真实验

为了验证本文中提出的电压电流双闭环控制器的优越性，分别采用普通的单闭环反馈控制方法和双闭环控制方法进行仿真实验，通过观察输出电压的波形实现对比分析。

首先采用普通的反馈控制方法，在Matlab/ Simulink环境下搭建单闭环控制系统仿真模型，如图8所示。这里扰动环节的选取参考文献［7］中的设计方法，考虑到输出电感电流的扰动会直接影响电流内环的功率级传递函数，在设计中选择幅值为2.4 A（10%的输出电感电流），频率为50 kHz的随机信号来模拟扰动信号。得到普通的基于偏差量的单闭环控制系统的仿真结果如图9所示。从中可以看出系统约经过6 ms才达到稳定，超调量很大，稳态纹波峰峰值为0.7 V，表明系统的稳定性和抗干扰能力较差。

图8　单闭环控制系统仿真模型

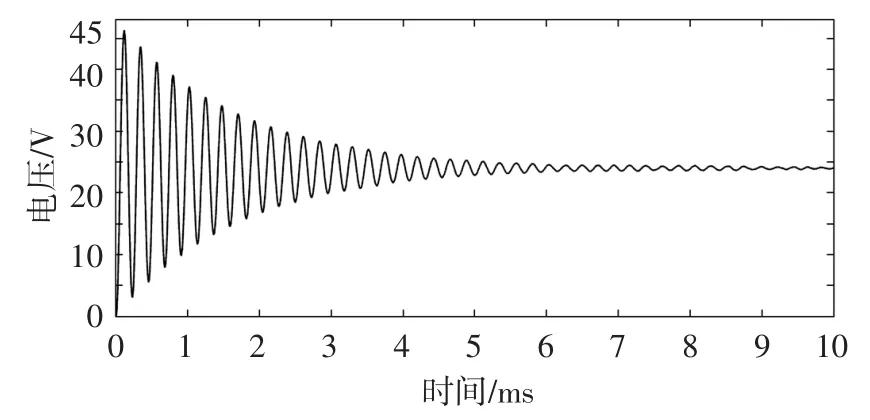
图9　单闭环控制系统电压输出波形

然后按照本文中前面设计的PI调节参数，搭建了电压电流双闭环控制系统的仿真模型，这里引入同样的扰动环节模拟电池充放电时电流波动对均衡系统的干扰，如图10所示。

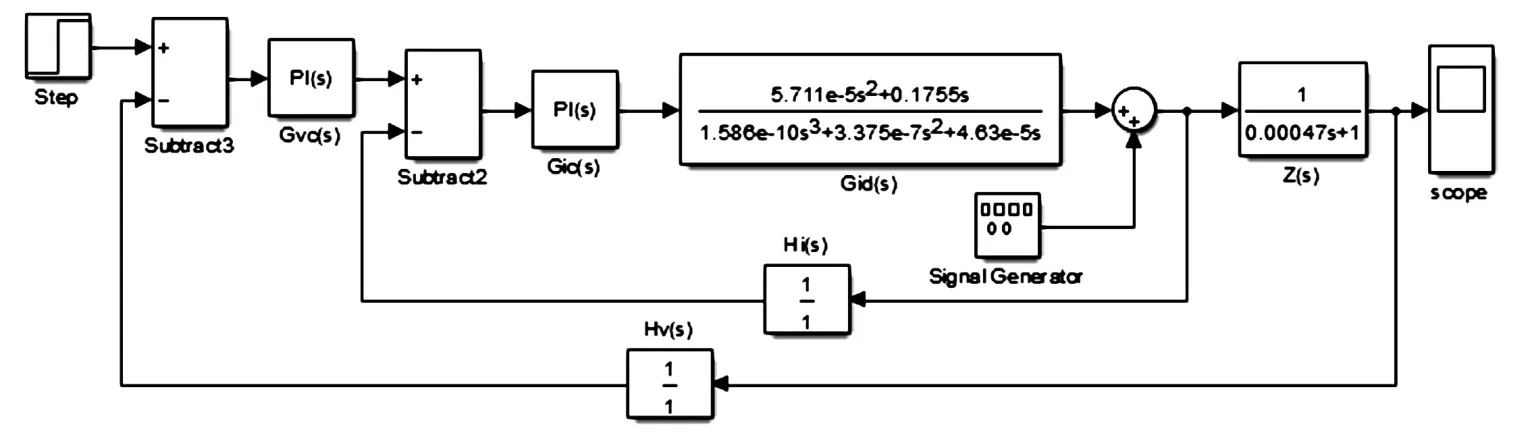
图10　双闭环控制系统仿真模型

图11为双闭环控制系统作用下的电压输出波形系统能够快速稳定在24 V，系统调节时间约为2.1 ms，超调量很小，稳态纹波峰峰值为0.06 V，说明系统具有很好的动态性、稳定性和抗干扰能力。

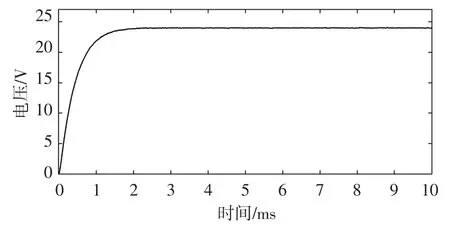
图11　双闭环控制系统电压输出波形

5　结束语

本文中对基于反激变换器的电池均衡系统的优缺点进行了分析，通过建立反激变换器的小信号模型，设计了电流内环和电压外环的PI调节器参数，完成了基于反激变换器电池均衡系统双闭环控制器的设计，并且在Matlab/Simulink环境下搭建了普通单闭环控制系统和电压电流双闭环控制系统的仿真模型来做实验对比论证。实验结果表明：该双闭环控制器具有更好的稳定性和动态性，并且能抑制电池充放电时电流波动对均衡系统的干扰。

［1］王丹，续丹，曹秉刚.电动汽车关键技术发展综述［J］.中国工程科学，2013，15（1）：68-72.

［2］Qi J，Lu D D C.Review of Battery Cell Balancing Techniques［C］//Power Engineering Conference（AUPEC），2014 Australasian Universities.IEEE，2014.

［3］Cao J，Schofield N，Emadi A.Battery Balancing Methods：A Comprehensive Review［C］//IEEE.Vehicle Power and Propulsion Conference，2008：1-6.

［4］刘红锐，张昭怀.锂离子电池组充放电均衡器及均衡策略［J］.电工技术学报，2015，30（8）：186-192.

［5］张卫平.开关变换器的建模与控制［M］.北京：中国电力出版社，2005.

［6］陈红，王聪，王俊.开关变换器建模、控制及其控制器的数字实现［M］.北京：清华大学出版社，2013.

［7］陈国超，张昆仑.移相全桥ZVS ZCS变换器双闭环控制系统设计［J］.通信电源技术，2010，27：20-23.

Simulation Design of Double-closed-loop Controller for Battery Equalizer Based on Flyback Converter

Wan Ming，Jiang Xuehuan，Jia Rong，Jian Wei
（School of Electrical&Information Engineering，Hubei University of Automotive Technology，Shiyan 442002，China）

The double-closed-loop controller was designed for a battery equalizer based on the flyback converter.The operating mode of the flyback converter was analyzed，the small signal model was established by the methods of the average model of switch device，and the PI regulator parameters of the current inner loop and voltage outer loop were designed.Finally，the simulation model of the double-closed-loop control system was built in the Matlab/Simulink environment.It is proved this method has some advantagesbycomparinganddemonstrating.

flyback converter；battery equalization；double-closed-loop control

U469.72+2；TP17

A

1008-5483（2016）03-0036-05

10.3969/j.issn.1008-5483.2016.03.009

2016-05-21

湖北省教育厅科学技术研究计划优秀中青年项目（Q20161805）；汽车动力传动与电子控制湖北省重点实验室开放基金项目（ZDK1201503）

万明（1991-），男，湖北黄冈人，硕士生，从事电动汽车电池管理系统、主动均衡技术的研究。E-mail：296655257@qq.com