武汉市PM10和PM2.5的分析及预测
黄小明,范雪敏,李治
(华中农业大学理学院,湖北武汉430000)
武汉市PM10和PM2.5的分析及预测
黄小明,范雪敏,李治
(华中农业大学理学院,湖北武汉430000)
采用相关分析、Granger因果检验和残差修正模型等对武汉市PM10和PM2.5进行定量分析。结果表明:PM10和PM2.5浓度均具有明显的季节性特征和空间差异性;PM2.5和PM10与SO2、NO2、CO呈正相关,与O3、最高温、最低温均呈负相关,与风力无关;下雨天可以显著降低空气中PM10和PM2.5的浓度;SO2、NO2、O3、最高温与PM10和PM2.5存在显著的格兰杰因果关系。采用残差修正模型分别预测武汉市PM10和PM2.5质量浓度,结果表明:预测精度优于传统的ARMA模型。
PM10;PM2.5;影响因素;预测
随着我国加快工业现代化和城镇化进程,石油、煤矿和天然气等化石燃料快速消耗,大量的大气污染物产生并排放到空气中。这些污染物集中排放、浓度高,加上地形和天气等因素综合影响,造成我国出现了严重的大气污染问题。2011年10月~2012年3月,我国长三角等地区出现了多次严重的雾霾天气[1]。
近年来武汉市的雾霾天气也频频发生。按照修订前的空气质量标准评价,2012年武汉市环境空气质量优良天数为321 d,优良率为87.7%。2013年武汉环境空气质量优良天数降到了仅有160 d,下降幅度达到了一半,优良率也仅有43.8%。颗粒物污染是武汉大气环境污染的主要问题之一,但相对于北京、广州等大城市,武汉市对颗粒物的研究较少。因此对武汉市的PM10和PM2.5进行影响因素分析并预测很有必要。
1 文献综述
20世纪90年代,国际上对PM10和PM2.5的研究主要集中在颗粒物的化学组成、存在状态、物理化学特征及其在大气中的变化、对人体健康的影响、源解析和对能见度的影响等方面。近年来随着我国雾霾天气频发,国内学者也对PM10和PM2.5进行了研究。张振华采用序列图比较和回归分析的方法分析PM2.5与各大气污染物和气象条件之间的相关关系,但没有对具体影响形式进行分析[2]。朱静茹等采用Pearson相关系数方法分析PM2.5和气压、风速、温度、降雨量及相对湿度的相关关系[3],但没有考虑到大气污染物之间的相互影响。我国对于PM10和PM2.5的影响因素分析不够全面。
为准确预测空气颗粒物,彭斯俊等采用ARIMA对武汉市PM2.5浓度进行预测,结果显示,相对误差在5%~35%之间[4],但只预测了一个日期。国外学者Perez等利用NN模型对PM2.5浓度进行预测,得到预测误差在30%~60%之间[5]。石灵芝等采用BP神经网络模型对PM10进行了预测,结果显示,BP神经网络预测R2为0.62[6]。有关武汉市PM10与PM2.5浓度研究的资料比较缺乏,定量分析预测的研究更是稀少。本文中将利用收集到的大气污染物和气象数据对PM10与PM2.5浓度进行定量分析、研究与预测,提出泛化能力和鲁棒性更强的预测模型,为PM10与PM2.5浓度的预警工作提供参考。
2 研究方法
采用的大气污染物2013年1月1日~2015年1月29日数据均从武汉市环保局官网中收集,所有气象数据均从天气后报网页中收集。对于缺失值采用临近两点均值进行插值。
对连续性数据变量之间的相关分析采用Pearson相关系数进行分析,对于风速这类等级数据与PM2.5和PM10的相关系数采用Spearman秩相关系数分析。采用Granger因果检验分析污染物之间的因果关系,并采用残差修正模型对PM10和PM2.5浓度。
ARMA(p,q)模型中既有自回归过程AR(p)又有移动平均MA(q)[7],其形式如下:
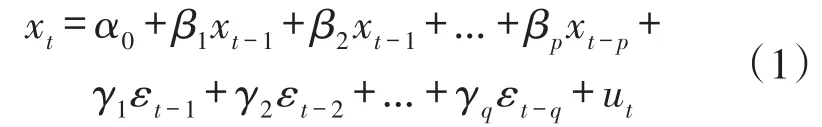
从式(1)中可看到,ARMA(p,q)模型只考虑了自身的影响,没有考虑其他影响因素的影响。所以根据实际需要采用如下残差修正模型:
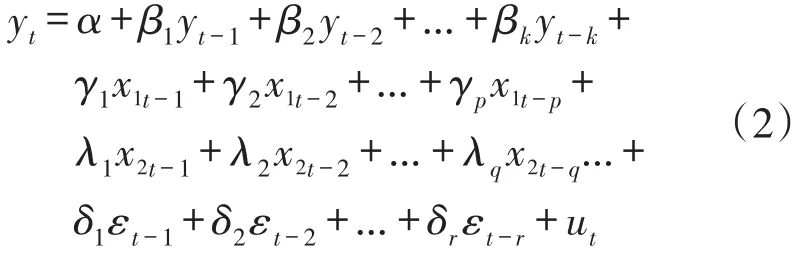
简化形式如下:
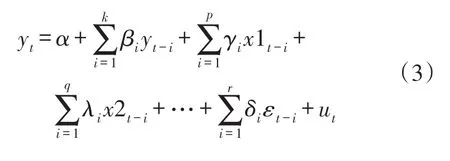
3 研究结果
3.1PM10和PM2.5时间分布分析
PM2.5质量浓度随时间变化如图1所示,可以看到:武汉市PM2.5日均浓度波动较大,且存在明显的季节趋势;春季的日均浓度普遍较高,夏季出现下降趋势,到了秋天基本保持相对较低的浓度,然后逐渐上升。从图2中可以明显看到,武汉市PM10日均浓度跟PM2.5日均浓度的变化基本相同。
冬季温度较低,生产生活供能增加将会排放较多的PM2.5和PM10。春冬季大气层较为稳定,降雨量大大减少不利于PM2.5和PM10的沉降。夏季特别6月份之后武汉市开始进入梅雨季节,大气层活动强烈,风速也较高,利于污染物扩散和沉降。
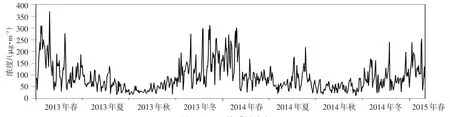
图1 PM2.5日均质量浓度

图2 PM10日均质量浓度
3.2PM10和PM2.5时空分布分析
对不同季节的PM2.5和PM10的浓度空间分布作图如图3~4所示。由图3可以看到,所有季节的PM2.5浓度空间分布基本相同。从图4可以看到,所有季节的PM10浓度空间分布基本相同。
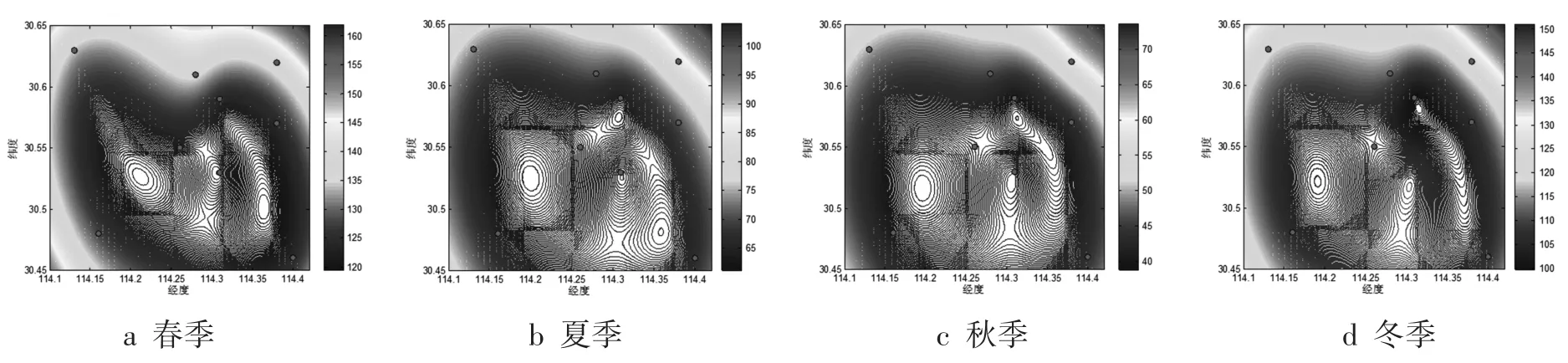
图3 不同季节PM2.5浓度空间分布

图4 不同季节PM10浓度空间分布
结合武汉市的地理分布可以知道,在蔡甸区拥有大面积的采矿点,而汉南区有大片旱田,湖泊面积相对较小,而江夏区由于近几年来的发展和建设,建筑业造成较大的粉尘排放。而在长江沿岸和洪山区及江夏区北部,由于高校数量较多,绿化程度高且湖泊较多,利于污染物的扩散和沉降,从而使得污染物浓度有所降低。
3.3PM10和PM2.5静态影响因素分析
连续性数据的变量之间的相关分析采用Pearson相关系数进行相关,风速属于等级数据,与PM2.5和PM10的相关分析采用Spearman秩相关系数分析。由于天气为名义变量,不能采用相关系数分析,采用单因素方差分析进行分析,后采用多重分析进一步比较不同天气状况下的PM10和PM2.5浓度值。相关系数如表1所示。
从表1可看到:PM2.5与PM10、SO2、NO2、CO呈正相关,其中PM10相关系数最大;与臭氧(8 h)、臭氧(1 h)最高温、最低温均呈负相关,其中最低温的相关系数最大;与风力相关系数没有统计学意义。
PM10与PM2.5、SO2、NO2、CO、臭氧(1 h)呈正相关,其中与PM2.5的相关系数最大;与最高温、最低温均呈负相关,其中与最低温的相关系数最大;PM10的质量浓度与风力、臭氧(8 h)的相关系数没有统计学意义。

表1 相关分析结果
虽然PM2.5可由其他气态污染物经过二次转化形成,但PM2.5与各大气污染物存在较强的相关性并不代表PM2.5主要是由这些气态污染物经过二次转化形成,而有可能反映出气态污染物与PM2.5有共同的来源。武汉环保局研究表明[8]:武汉市PM2.5污染25%左右来自工地和道路扬尘,大约24%来自工业生产,16%来自煤炭燃烧,20%左右来自汽车排放,其他来自不确定源、区域相互影响以及二次污染物。从中也可以看到,二次转化并不是PM2.5污染的主要原因。
大气中的SO2来自于煤炭燃烧和工业生产,NO2主要来源于汽车尾气排放和化石燃料燃烧、CO主要来源于汽车尾气排放和煤炭燃烧,PM2.5与PM10、SO2、NO2、CO呈正相关可以反映出武汉市煤炭燃烧、工业生产、汽车尾气排放和化石燃料燃烧会显著增加PM2.5的污染。
PM2.5与臭氧(8 h)、臭氧(1 h)最高温和最低温均呈负相关,而臭氧多来自于光化学反应,在太阳辐射较强和温度较高的条件下容易产生,一方面臭氧会通过二次转化增加PM2.5污染,但由于其在浓度较高时大多在夏季,而夏季时武汉多风多雨,这使得PM2.5极易扩散和沉降,最终臭氧所产生的PM2.5速度不如扩散和沉降的速度,表现出臭氧和PM2.5呈负相关。温度对PM2.5影响的原因也是如此。
PM2.5与风力没有显著统计学意义,是因为武汉的风力绝大部分均在3级以下,风力对PM2.5的作用不能显著表现出来。
PM10与PM2.5相同,主要受到煤炭燃烧、工业生产、汽车尾气排放和化石燃料燃烧的影响,但PM10的粒径较大,很少是通过二次转化而来,所以与臭氧的相关系数非常小。温度和风力对PM10的影响形式与PM2.5的影响形式基本相同。
3.4PM10和PM2.5动态影响因素分析
PM10和PM2.5的动态影响因素进行分析,结果如表2所示。可以看到:对于PM2.5,滞后1阶PM2.5的Granger原因有SO2、NO2、最高温和最低温;而滞后2阶,PM2.5的Granger因素有SO2、NO2、臭氧(8h)、臭氧(1 h)、最高温和最低温;滞后3阶PM2.5的Granger因素SO2、NO2、臭氧(8h)、臭氧(1h)、最高温和最低温;滞后4阶的PM2.5Granger原因有SO2、NO2、PM10、臭氧(8h)、臭氧(1h)、最高温和最低温。
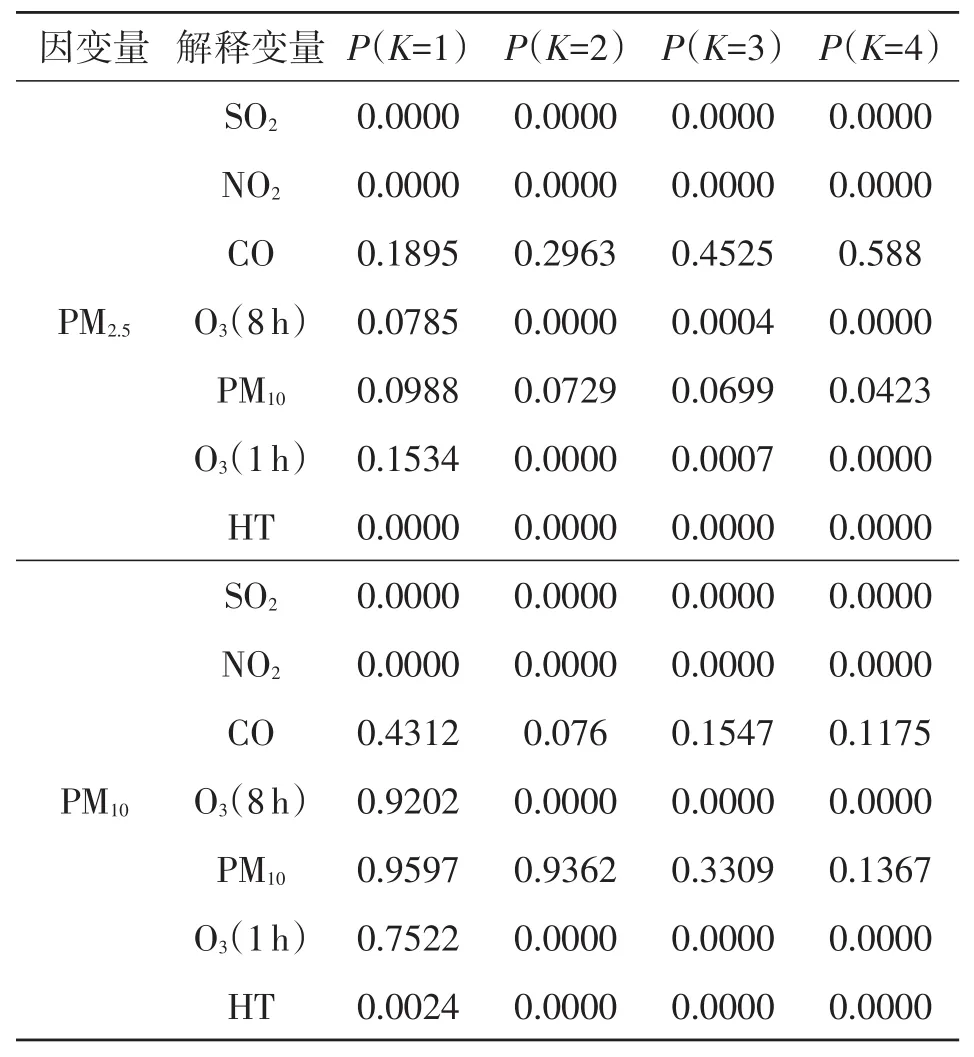
表2 Granger因果检验结果
而对于PM10,滞后1阶的PM10的Granger原因有SO2、NO2、最高温和最低温;而滞后2阶,PM10的Granger因素有SO2、NO2、臭氧(8 h)、臭氧(1 h)、最高温和最低温;滞后3阶PM2.5的Grange因素SO2、NO2、臭氧(8 h)、臭氧(1 h)、最高温和最低温;滞后4阶的PM2.5Grange原因有SO2、NO2、臭氧(8h)、臭氧(1 h)、最高温和最低温。
综合以上结果可以知道,影响PM10和PM2.5的因素基本相同,近期的SO2、NO2、臭氧(8 h)、臭氧(1 h)、最高温和最低温是影响当日PM10和PM2.5的主要因素。而CO对PM10和PM2.5没有显著影响。
3.5基于残差修正模型的PM10和PM2.5浓度预测
根据格兰杰因果检验结果,选出滞后1~2阶中任意有一个通过检验的变量作为自变量,可以得到:PM2.5(SO2、NO2、臭氧(8h)、臭氧(1h)、最高温、最低温);PM10(SO2、NO2、臭氧(8h)、臭氧(1h)、最高温、最低温)。
结果如表3所示,R2为0.71,说明模型拟合优度较好,F统计量P值为0.0000,说明得到模型是显著成立的。D-W统计量为2.00,说明该模型的残差不存在自相关。根据上述结果可对PM2.5进行预测,本文中对样本外5个样本进行预测,并与实际值对比得到结果如图5所示。从图5中可以看到:预测效果较好,平均相对误差误差仅为11.8%。
结果如表4所示。R2为0.645,说明模型拟合优度较好,P值为0.0000,说明得到模型是显著成立的。D-W统计量为1.999,说明该模型的残差不存在自相关。根据结果可对PM10进行预测,5个样本外预测预测值和实际值对比如图6所示。从图6中可以看到:PM10的预测模型预测效果也较好,平均相对误差为16.4%。
为说明残差修正模型效果优于一般的ARMA模型,采用ARMA模型对PM2.5和PM10进行预测,结果表明,ARMA模型预测PM2.5的拟合优度为0.66,平均相对误差达到了33.70%,ARMA用于预测PM10拟合优度也仅为0.56,相对误差为38.90%。相对于残差修正模型,ARMA模型的拟合优度均有所降低,相对误差均有所上升,由此说明残差修正模型相对于一般的ARMA模型引入了多因素的影响,能更好地用于预测PM2.5和PM10质量浓度。
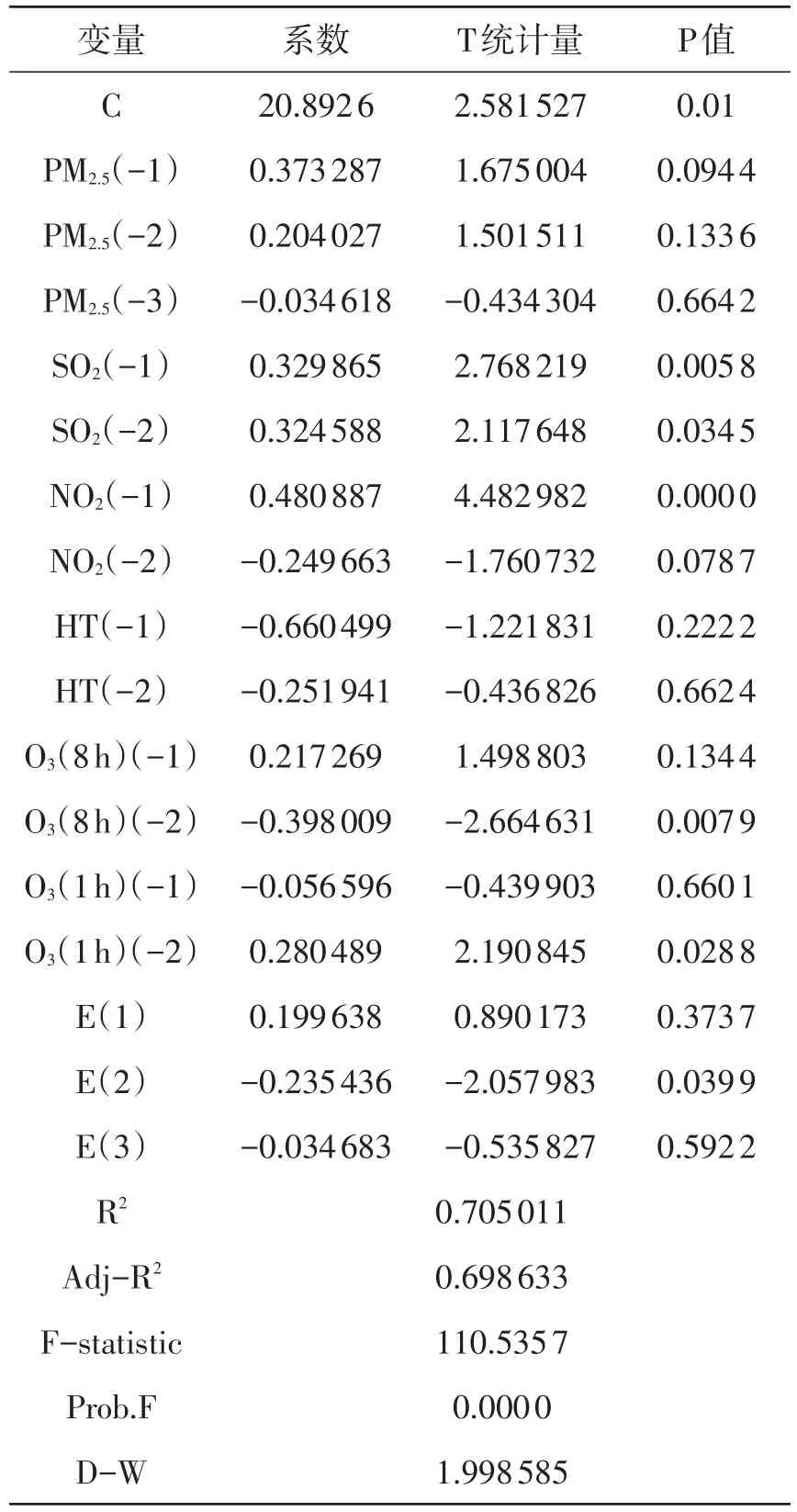
表3 PM2.5预测模型参数估计结果
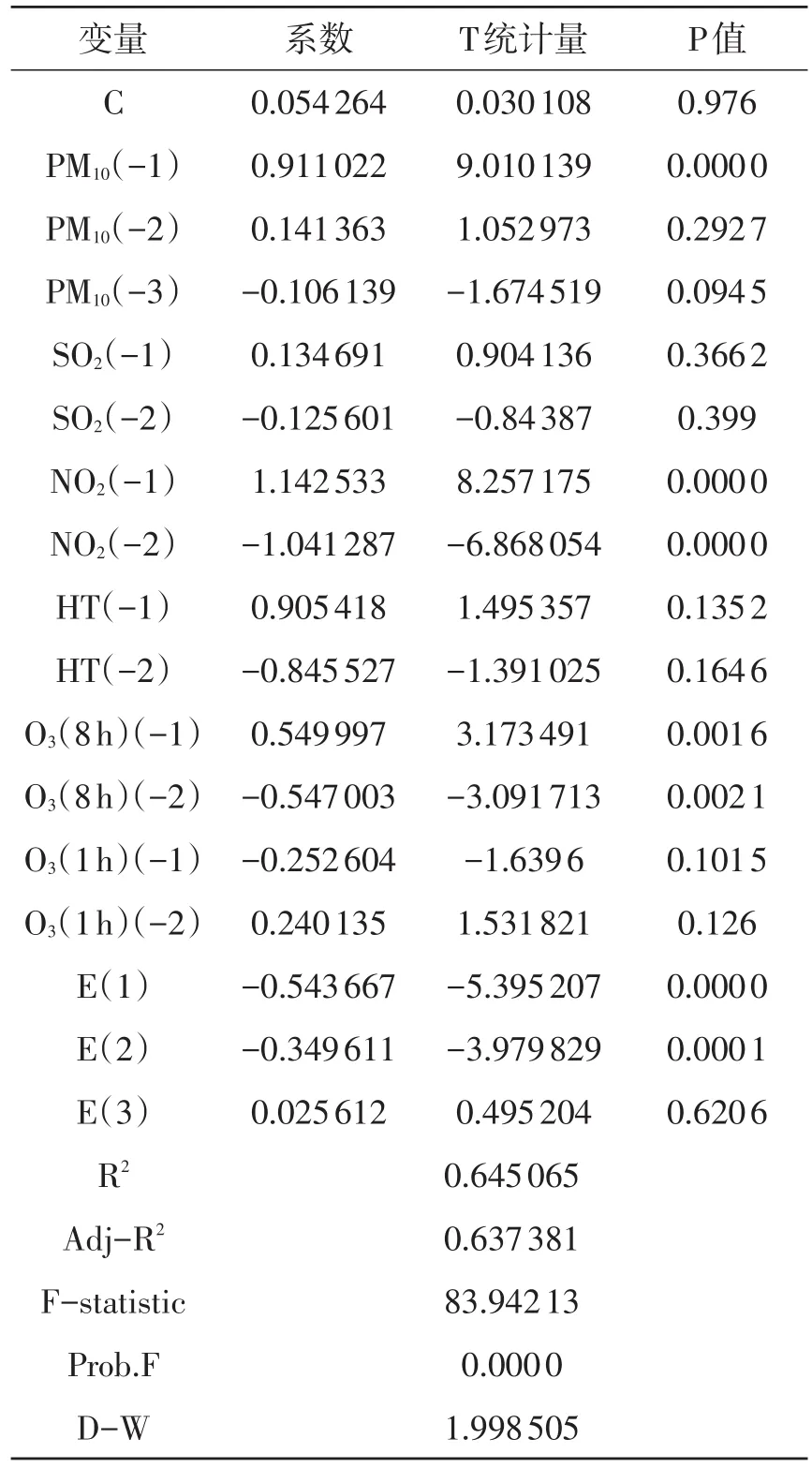
表4 PM10预测模型参数估计结果

图5 武汉市PM2.5质量浓度预测结果图
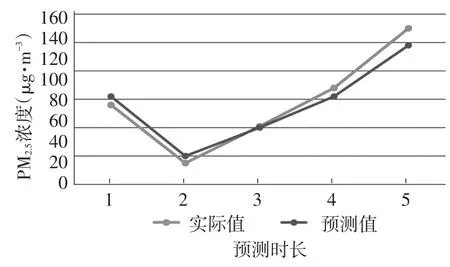
图6 PM10质量浓度预测结果图
4 结论
通过定量分析发现:武汉市PM10和PM2.5的时间具有明显季节特征,同时具有空间特性。PM10和PM2.5不仅受到当日气象和污染物浓度的影响,还受到历史气象条件和污染物浓度的影响。采用残差修正模型分别预测武汉市PM10和PM2.5质量浓度,结果显示:相对于传统的ARMA模型,残差修正模型能够更好的预测PM10和PM2.5浓度,模型的拟合优度分别为0.645 1和0.705 0,平均相对误差分别为37.40%和30.70%。仅对城区的PM10和PM2.5进行时间分布、空间分布等分析,没有对不同监测点分别进行分析,因为不同的监测点的分布可能不同。本文中采用残差修正模型虽然能够提高拟合优度,降低相对误差,提高预测精度,但效果并不非常明显。
[1]吴兑.探秘PM2.5[M].北京:气象出版社,2013:1-3.
[2]张振华.PM2.5时空变化特性、影响因素及来源解析研究[D].杭州:浙江大学,2014.
[3]朱倩茹,刘永红,徐伟嘉,等.广州PM2.5污染特征及影响因素分析[J].中国环境监测,2013,2:15-21.
[4]彭斯俊,沈加超,朱雪.基于ARIMA模型的PM2.5预测[J].安全与环境工程,2014(6):125-128.
[5]Perez P,Trier A,Reyes J.Prediction ofPM2.5Concentrations Several Hour in Advance Using Neural Networks in Santiago,Chile[J].Atmospheric Environment,2000,34:1189-1196.
[6]石灵芝,邓启红,路蝉,等.基于BP人工智能网络的大气颗粒物PM10质量浓度预测[J].中南大学学报,2012(5):1969-1974.
[7]汪晓银,周保平,齐立美,等.数学建模与数学实验[M].北京:科学出版社,2012:38-40.
[8]武汉环保局.武汉市PM2.5组分研究[EB/OL].[2016-04-07].http://news.cnhubei.com/xw/wuhan/201412/ t3115166.shtml,2014.
Analysis and Prediction of PM10and PM2.5in Wuhan City
Huang Xiaoming,Fan Xuemin,Li Zhi
(Faculty of Science,Huazhong Agricultural University,Wuhan 430000,China)
The quantitative analysis ofPM2.5andPM10in Wuhan city was carried out by the correlation analysis,Granger causality test and error correction model.The results indicatePM2.5andPM10concentrations have obviously seasonal and spatial characteristics.PM2.5andPM10that have nothing with wind are positivelycorrelatedwithSO2,NO2andCO,butnegativelycorrelatedwithO3,thehighesttemperatureandthelowest temperature.In raining days,the concentrations ofPM2.5andPM10in the air decrease significantly. There is significant Granger causality between SO2,NO2,O3,the high temperature withPM2.5andPM10.The concentrations ofPM10andPM2.5in Wuhan city were forecasted by the error correction model.The results indicatethepredictionaccuracyisbetterthanthetraditionalmodelofARMA.
PM10;PM2.5;influencing factors;forecast
F812.42;F407.471
A
1008-5483(2016)03-0072-05
10.3969/j.issn.1008-5483.2016.03.017
2016-04-07
黄小明(1992-),男,广西百色人,硕士生,从事经济统计学方面的研究。E-mail:15377598670@163.com

