基于季节性ARIMA模型的河流观测点流量的时序分析

郑江松

（湖北工业大学电气与电子工程学院，湖北武汉430068）

基于季节性ARIMA模型的河流观测点流量的时序分析

郑江松

（湖北工业大学电气与电子工程学院，湖北武汉430068）

采用季节性ARIMA模型拟合1960～2009年某河流观测点流量。通过比较，得到ARIMA（1，0，0）×ARIMA（0，1，1）12模型，并用这一模型预测2010年1～12月的流量，预测效果显著。

流量；ARIMA模型；差分；时间序列

河流流量是指单位时间内通过某一过水断面的水量。影响河流流量的因素很多，包括雨水、融水、支流补充、流域内植被分布、人类利用等方面，其变化趋势既存在确定性，也存在不确定性因素影响，目前很难通过数值模拟准确预测某个观测点的流量［1-2］。笔者以某河流观测点1960～2009年流量数据为基础，对流量时间序列进行数学建模，使用R软件［3］进行多次拟合试验，并比较了2010年实际流量与预测流量。

1　研究对象与数据来源

研究对象为甘肃省某河流某观测点径流量；本文中用到的原始数据来源于当地水文观测站1960～2009年实际观测的数据。

2　分析方法

2.1季节性ARIMA模型原理

ARIMA模型是由统计学家Box与Jenkins共同提出的，也叫Box-Jenkins模型，旨在解决含有确定趋势的非平稳时间序列的建模问题［4-5］。基本思想是：1）通过差分，将非平稳过程变为平稳过程；2）进行模式识别，建立最优模型能够描述这一过程；3）预测趋势。

ARIMA模型分为ARIMA（p，d，q）模型和ARI-MA（p，d，q）×（P，D，Q）S季节乘积模型，前者用于拟合差分后具有短期相关性的时间序列，后者为具有季节性的时间序列建模。本文中所采用的模型为后者，其具体模型结构如下：

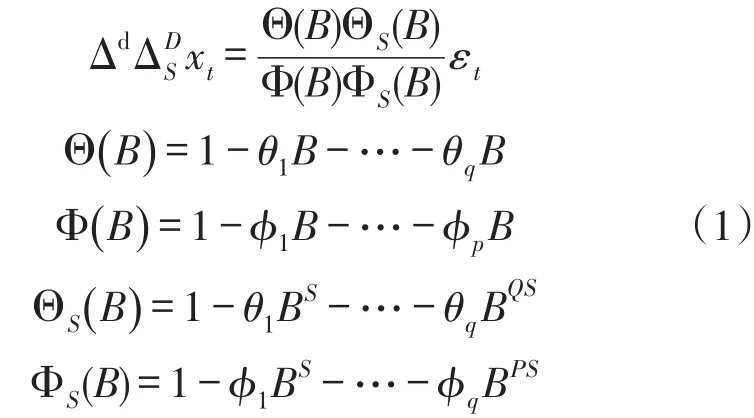
式中：S为步长。

2.2建模步骤

1）数据的初始操作，对序列进行处理使其满足模型假设，本文中对序列进行了对数处理。

2）进行平稳性检验，检验序列是否平稳。

3）由自相关和偏自相关分析得到季节性周期T。

4）对序列尝试差分运算，消除季节性影响，得到平稳序列，从而确定出d和D。

5）模型的识别与定阶根据自相关函数与偏自相关函数的形态，通过尝试，确定p，q和P，Q，对于混合模型，很难明显地对模型定阶，因此在实际应用中阶数一般选择0，1，2。通过不同的阶数组合，根据其BIC值，选择最为合适的p，q和P，Q值。

6）对未来趋势进行预测。

3　结果与分析

3.1数据的平稳性分析和初始处理

通过时序图（图1），可看出流量变化较大，具有明显的季节周期性，而且年与年之间的差别也较大，因此可断定流量为非平稳时间序列，为了使数据波动幅度基本稳定，对数据进行对数变换，即

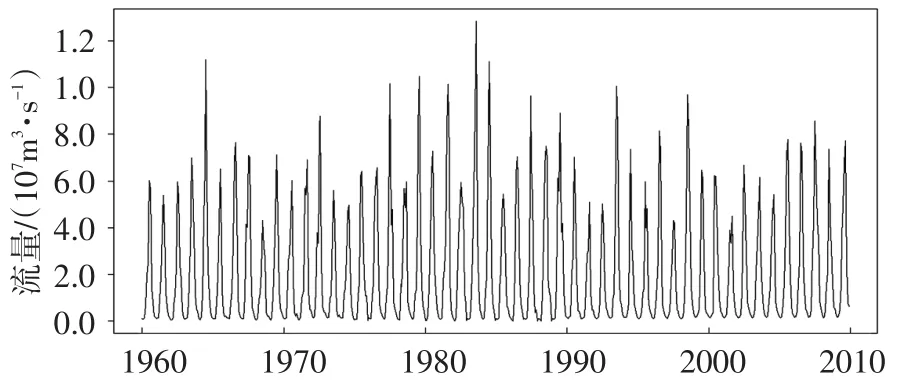
图1　河流流量时序图

图2 a反映出自相关系数的衰减过程，其值衰减过程缓慢，呈现出明显的正余弦波动规律；图2 b反映的是偏自相关函数的衰减过程，其值也没有迅速衰减为0。

图2　河流流量偏自相关图

3.2对序列进行差分处理

由于序列本身并不存在明显的上升或者下降趋势，仅具有季节性的周期性趋势，对该序列进行平稳性处理，只需对序列进行一次1阶12步的差分处理，此时d为0，D为12。

图3 a表明其自相关系数拖尾，12阶出现较大的自相关系数，24阶和36阶的自相关系数也在2倍的标准差外；图3 b表明其偏自相关系数1阶迅速截尾，除了12阶、24阶和36阶的偏自相关系数在2倍标准差外，其余大部分在2倍标准差以内。

图3　1阶12步差分后序列的自相关和偏自相关图

3.3定阶尝试与检验

根据1阶12步差分后序列的自相关图与偏自相关图，可以尝试根据最小BIC值找到最优模型。

1）ARIMA（1，0，0）×ARIMA（0，1，2）12BIC统计量为775.69。

2）ARIMA（1，0，0）×ARIMA（0，1，3）12BIC统计量为775.86。

3）ARIMA（2，0，0）×ARIMA（0，1，2）12BIC统计量为780.56。

4）ARIMA（1，0，0）×ARIMA（0，1，1）12BIC统计量为770.32。

比较发现ARIMA（1，0，0）×ARIMA（0，1，1）12模型的BIC统计量最小，因此选择这一模型。

3.4模型检验

一个好的模型应该满足如下要求：1）标准化的残差没有波动性聚集；2）残差的自相关函数没有显著的自相关性；3）Ljung-Box统计量的p值都高于显著性水平，表明残差没有任何模式，模型中的信息已经完全被提取，剩余的仅仅是噪声。

通过R软件的tsdiag函数产生标准化残差图，残差自相关图和LB统计量图。通过图4可以发现标准化残差没有波动率聚集；图5的残差自相关函数0阶截尾，说明残差不存在自相关关系；图6的LB统计量都在0.05的显著性水平之上。从而可以断定序列的信息被完全提取，剩余的仅仅是噪声。

图4　标准化残差图

图5　残差自相关函数图

图6　LB统计量图

3.5模型预测

根据上述所选的模型，估计出参数AR1为0.253 7，SMA1为-0.735 4。因此模型可以表示为

根据上述模型，该河流观测点预测2010年1～12月流量数据见表1。由表1可看出：对某河流观测点月流量，使用季节乘积ARIMA模型建模，建立的ARIMA（1，0，0）×ARIMA（0，1，1）12模型预测效果显著，因此所建立的模型具有一定的实际意义。

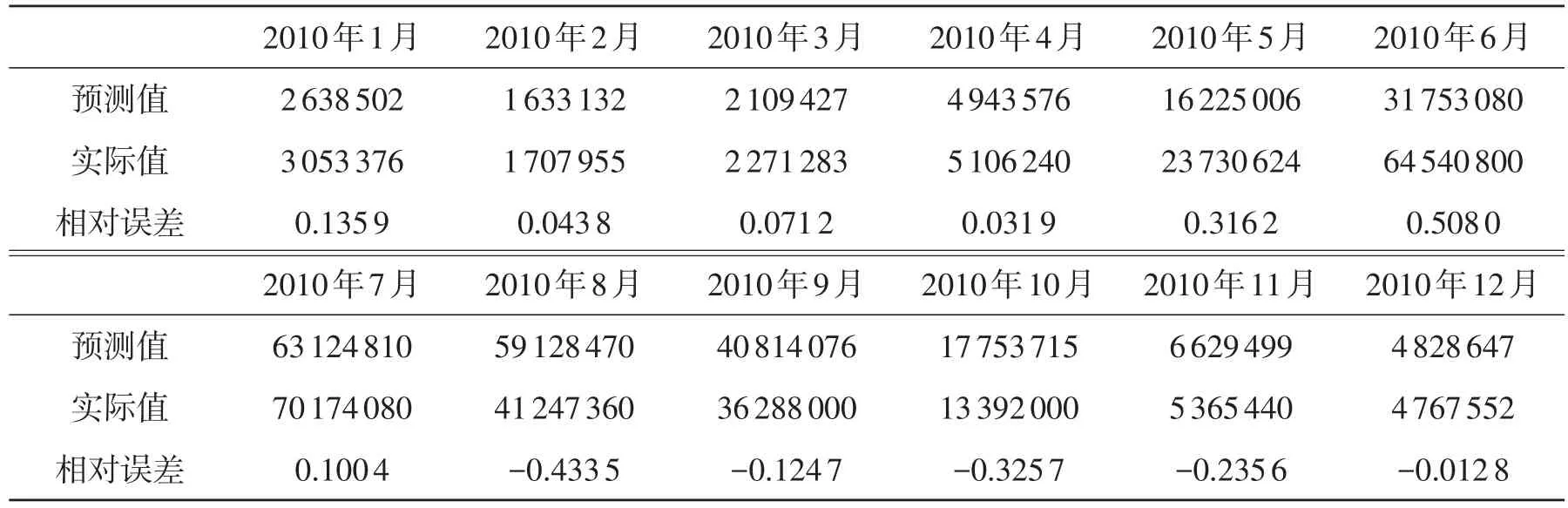
表1　根据模型所做的预测值、实际值和相对误差

［1］安鸿志，陈兆国，杜金观，等.时间序列的分析与应用［M］.北京：科学出版社，1983：124-150.

［2］杨位钦，顾岚.时间序列分析与动态数据建模［M］.北京：北京理工大学出版社，1988：163-189.

［3］J H Maindonald.Statistical Computation［M］.New York： John Wiley，1984：193-215.

［4］S M Pandit，Shien Ming Wu.Time Series and System Analysis with Applications［M］.New York：John Wiley，1983：142-165.

［5］Box G E P，Jenkins G M.Time Series Analysis，Forecasting and Control［M］.San Francisco：Holden Dovy，1970：157-182.

Time Series Analysis on Flow of Observation Point for a River Based on Season ARIMA Model

Zheng Jiangsong
（School of Electrical and Electronic Engineering，Hubei University of Technology，Wuhan 430068，China）

Flow of the observation point for a river from 1960 to 2009 was simulated with season ARIMA model.As a result，ARIMA（1，0，0）×ARIMA（0，1，1）12 model was obtained.Flow of the river in 2010 was alsoforecasted with themodel.Theresultsshowtheforecastingabilityofthemodelisstrong.

flow；ARIMA model；difference；time series

C81；O212

A

1008-5483（2016）03-0069-03

10.3969/j.issn.1008-5483.2016.03.016

2016-04-07

郑江松（1991-），男，湖北武汉人，硕士生，从事应用经济学方面的研究。E-mail：2107643098@qq.com