一种新型Powell粒子群算法同步综合换热网络

张春伟，崔国民

（上海理工大学新能源科学与工程研究所，上海 200093）

一种新型Powell粒子群算法同步综合换热网络

张春伟，崔国民

（上海理工大学新能源科学与工程研究所，上海 200093）

针对换热网络同步综合方法的不足，本文提出了一种新型Powell粒子群算法，具有传统确定性方法的高精度以及启发式方法的高效率。同时针对群体智能算法优化换热网络问题时存在的不足，提出了云记忆体和个体对立策略，有效地避免算法发生早熟现象，扩大搜索范围。为处理整型变量而提出的两条整型变量优化策略与 Powell粒子群算法结合，实现了连续变量与整型变量的同步优化。最后，选取两个经典算例验证算法的性能，均获得了优于文献的结果，表明算法能够找到更优的换热网络结构，是一种处理混合整数非线性问题的有效方法。

换热网络综合；整型变量优化；Powell法；群体智能

换热网络综合（heat exchanger network synthesis，HENS）是过程系统工程的一个重要领域，其目的是发现一个能量回收最大或者年综合费用（包括投资费用和运行费用）最小的换热网络结构，进而提高能量利用率和经济性。换热网络综合问题的复杂性很大程度源于其换热器的组合本质，FURMAN等［1］证明其为NP-难问题，因此即使是小规模的换热网络问题也很难证实得到全局最优解。

换热网络综合方法可分为分步综合方法和同步综合方法两类［2］。夹点技术法［3］由于其操作简便、观点明确，是一种在工程上应用较多的分步综合方法。但由于不能很好地权衡投资费用与能量回收，只能获得次优解。同步综合方法［4］的数学模型属于混合整数非线性规划范畴（mixed integer non-linear programming，MINLP），而基于同步综合模型的全局优化方法可进一步分为确定性方法和启发式方法［5］。确定性方法如分支定界法［6］、外部逼近法［7］等，但其在处理大规模换热网络问题时效率低下。启发式方法已在换热网络问题中得到了一定的应用，如遗传算法［8］、微分进化算法［9］、粒子群算法［10］等。此类算法通过仿生自然过程具有较强的全局搜索能力，但易受种群多样性等因素的影响，发生早熟等现象，进而陷入局部最优解。此外，由于不需要目标函数的梯度等信息，所以其求解精度有限。

在优化换热网络这类非凸、非线性严重的MINLP问题时，效率和精度一直认为是评价算法性能的两个重要指标，而常用的同步综合方法受限于其优化机理，很难兼顾两者。传统的确定性方法对初始点的依赖性较大，只能得到局部区域内的最小解。但依赖于梯度或方向的优化特性，使其具有较高的精度。所以在一些研究［11-13］中，此类算法会作为启发式方法的局部搜索策略，即在前者的搜索机理不变的情况下，增加算法的精度。但此种结合方式未充分发挥两种算法的优点，在优化换热网络时，会使算法的计算时间无限增长并忽略大量的较优解。

鉴于此，本文提出了一种新型 Powell粒子群算法（Powell particle swarm optimization algorithm，PPSO），将传统确定性方法的高精度、收敛速度快的特性与启发式方法的全局搜索能力相结合，同步综合换热网络。在算法中，每个粒子均具有Powell法的局部优化能力，通过构造新的启发式准则将所有粒子组织起来，使其具备全局搜索能力以及移动特性。并针对换热网络问题以及算法特性，提出了云记忆体和个体对立策略，扩大算法的搜索范围，避免早熟现象的发生。同时为处理问题中的整型变量，提出两条相关的整型变量处理策略。最后，通过两个经典算例对算法的性能进行了验证。

1 换热网络数学模型

1.1 换热网络问题数学描述

换热网络综合问题可表述如下：现有 NH股热流体、NC股冷流体，分别需要冷却、加热到相应的目标温度。在冷、热流体之间设置多个换热器，实现能量回收。当某一股流体未达到目标温度时，为其匹配冷或热公用工程。过程流体和公用工程的热容流率、进出口温度以及换热器换热系数均已知。以年综合费用为优化目标，包括运行费用和投资费用两部分，运行费用为消耗冷、热公用工程时产生的费用，投资费用为设置换热器时产生的费用，可分为面积费用和固定投资费用。

对于有分流的换热网络模型而言，虽然有时能够得到相对无分流模型费用值更低的换热网络设计，但由于其增加了问题的复杂性，而且没有计算由于流体分流引起的管路、阀门等造成的额外投资费用，所以在实际工程中的可接受度不高。鉴于此，本文采用GROSSMANN等［4］提出的无分流分级超结构模型，其中，换热网络的级数为NS=max（NH，NC），换热器的最大个数为NK=NS×NH×NC。现以2股热流体和2股冷流体为例表述分级超结构模型，如图1所示。

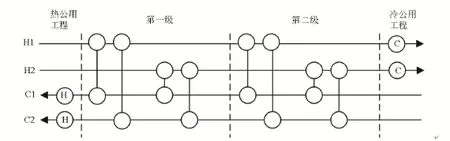
图1 换热网络无分流的分级超结构

1.2 优化的目标函数

针对上述换热网络模型，以年最小年综合费用为优化目标，其数学函数为式（1）。

式中，B为0-1整型变量，表示换热器有无。当换热器存在时，B=1，反之，则B=0；CCU、CHU分别为冷、热公用工程的费用系数；CF为设置换热器时的固定投资费用；CE为面积费用系数；Z为面积费用指数；QHU，j、QCU，i分别为热公用工程与冷流体之间的换热量和冷公用工程与热流体之间的换热量；AHU，j、ACU，i分别为其相应换热器的面积；Ai，j，k为冷热流体之间换热器面积。本文以单个换热器的换热量Qi，j，k为优化变量，各换热器均采用逆流传热方式，如式（2）～式（4）。

1.3 约束条件

2 Powell粒子群算法

Powell粒子具有找到所在区域局部最优的能力，所以粒子更容易发生聚集。鉴于此，本算法的中心思想是使粒子最大程度地遍历搜索空间同时避免发生早熟现象。Powell法一种求解无约束最优化问题的直接搜索法［14］，具有收敛速度快、求解精度高、无需计算导数等优点，较其他传统的局部优化方法更适合换热网络综合问题。Powell法的优化换热网络问题时的计算步骤如下所示。

2.1 Powell法计算步骤

Step 1 确定变量维数N，即粒子结构的所包含的换热器个数，读取当前位置信息Q0。设置收敛精度ε1。给定一组线性无关的方向 Di（i=1，2，…，N），Di取个坐标轴的N个方向，即N阶单位矩阵。其中N的最大取值为NK。

Step 2 从初始点 Q0出发依次沿方向 Di（i=1，2，…，N）进行一维搜索，确定每次迭代的步长 ，得到Q1，Q2，…，QN，见式（32）、式（33）。

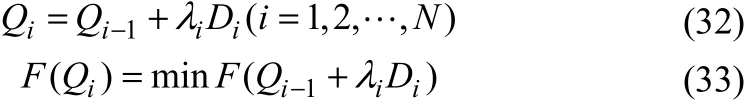
Step 3 判断迭代计算是否结束：若满足式（34），则得到解QN，计算结束；否则转Step 4。

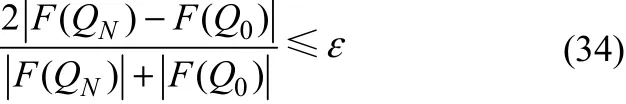
Step 4 计算最速上升方向上函数 F（Q）的变化，见式（35）。

Step 5 引进第（N+1）个搜索方向和新的点Qt，见式（36）、式（37）。并计算F（Qt）。

Step 6 方向替换判断。

①若满足

则将 QNh作为新的初始点，沿原方向搜索，即转Step 2。

③若满足

则将 QN作为新的初始点，沿原方向搜索，即转Step 2。

③若以上两条件均不满足，则转Step 7。

Step 7 以QN作为起始点，沿方向DN+1进行一维搜索，并得到此方向上的极小值点QN+1。将方向Dibig用新方向DNh+1替换，产生一组新的方向Di（i=1，2，…，N），以QN+1作为新初始点，转Step 2。

2.2 粒子的更新公式

根据算法的中心思想以及群体智能算法，本文提出了如式（40）的Powell粒子更新公式。

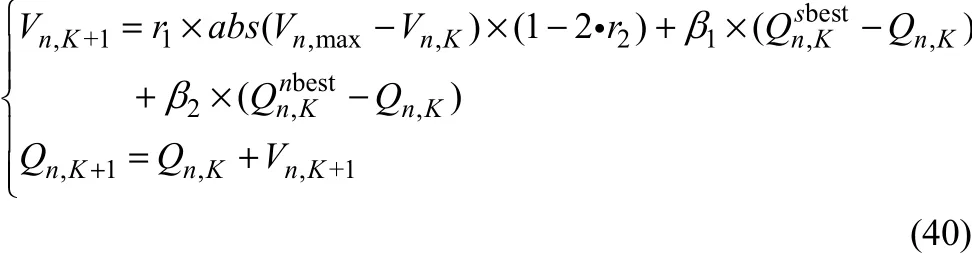
式中，r1和r2为介于（0，1）之间的伪随机数；1β和2β为非负常数；Vn，max为粒子的最大飞行速度；为粒子自身存储的最优位置；为粒子邻居的最优位置。公式第一项为随机扰动项，调整粒子的飞行速度和方向。当粒子的飞行速度较大时，其本身的随机搜索能力较弱，当粒子本身速度较小时，则产生一个相对较大的随机向量。由于算法是在保证种群进行信息交流的前提下，最大程度地遍历搜索空间，所以此项可以避免算法发生早熟现象。第二项与第三项分别为个体向自身最优与邻居最优的飞行的方向向量。即Powell粒子会根据随机搜索项、自身最优以及群体最优位置调整下一次的飞行方向并记忆搜索到的最优位置。

2.3 冯诺依曼拓扑结构

拓扑结构影响着算法的收敛速度以及精度等，其总体上可分为全局拓扑和局部拓扑两种。全局拓扑结构虽然收敛速度快，但易于陷入局部最优解。鉴于此，本算法采用局部拓扑中的冯诺依曼拓扑结构，如图2所示。每个Powell粒子只有4个邻居，相应的为邻居中的最佳位置。当一个粒子找到较好解时，只影响其周围的4个个体，这样可以较好地维持种群多样性。使得种群中的粒子向不同的最优位置靠拢，不易陷入局部最优。计算结果表明，此种拓扑结构对于复杂的问题具有良好的收敛性能，适用于解决换热网络综合问题。

图2 冯诺依曼拓扑结构

2.4 云记忆体

在群体智能算法中，个体的记忆能力是一个很重要的部分，能够指导个体搜索到更优的位置。如果算法采用常规的信息存储方式，即个体只记忆自身搜索到的最佳位置，可能会导致种群搜索到的一些较优解被忽略。例如，记录着种群当前最优位置的Powell粒子的记忆很难更新，除非发现了新的种群最优解，那么差于当前最优位置却优于其他个体记忆位置的解则会被算法遗失。

鉴于此，本文将相互独立的个体记忆功能统一组合为整个种群的记忆功能，即云记忆体，其内部保存的信息个数等于种群中的个体数，并且所有信息已按照适应度值的大小进行排序。当一个新解产生后，与种群记忆体中适应度值最差的位置信息进行比较，若优于此解，则将新解与记忆体中的所有信息再次进行排序，进而剔除最差的位置信息；若差于此解，则记忆体保持不变，算法继续进行搜索。根据云记忆体的思想，个体与其存储的最优位置信息不再有直接的联系，即其存储的信息可能为自身搜索到的，也可能为其他个体搜索到后存储在当前个体上。以图3所示为例说明云记忆体存储方式，假设种群中共有4个Powell粒子，那么云记忆体中则包含4个最优位置信息，并分别存储在不同的粒子上。通过云记忆体，算法能够克服常规信息存储方式的不足。此外，本文的粒子更新公式基于自身与邻居最优位置，所以云记忆体也会增加算法的随机性，扩大搜索范围。

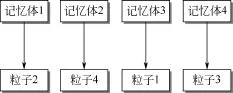
图3 种群云记忆体

2.5 个体对立策略

Powell粒子能够得到局部区域的极小值，所以当某些粒子处在一个相同的区域时，可能会发生聚集，弱化算法的性能。所以为了提高算法的搜索效率同时扩大搜索范围，提出个体对立策略，处理陷入局部最优的粒子。粒子状态的判定公式如式（41）、式（42）所示。

Smove表示Powell粒子的当前移动距离，当其小于一个设定的值时，认为此粒子陷入局部最优区域，此时通过个体对立公式变换粒子的位置，如式（43）。

式中，Qn，K为Powell粒子的当前位置；为对立后产生的新位置；为粒子n的搜索区间上限，即为换热器所在流体的最大换热潜能。由于算法能够不断地跳出局部最优解，所以具有很强的“爬山”能力。

3 整型变量优化策略

随着换热网络问题规模的日益增大，导致整型变量急剧增加，可行结构数量呈几何级增长，所以同步综合换热网络问题时，有效的整型变量优化技术不可或缺。鉴于此，本文提出了两条相关的整型变量优化策略。为准确表示换热网络结构，此处采用一种数字序列表达方式，两者的转换公如式（44）所示。由其可知，当换热器不存在时，序列中对应的数字为零，所以为表述简洁，序列中只包含存在的换热器，零则不予表述。详细转换过程如图 4所示。

图4 4股流换热网络结构及其序列表示

3.1 整型变量判断策略

在算法初始化阶段，设定个体的初始解均为全结构，即所有换热器都存在。通过测试发现，计算过程中，粒子某一维的换热量Q近似为零。从投资费用方面分析，当换热器上的热负荷小于一个特定的值时，可以认为此换热器对于减少年综合费用值是不利的，即这一维表示的换热器应该消去。但由于精度的影响，优化变量Q不可能完全为零。鉴于此，本文提出了一条整型变量判断策略，其形式如式（45）所示。

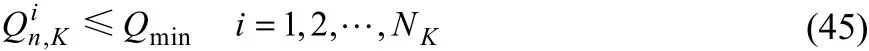
式中，Qmin为设定的换热器最小换热量，当Powell粒子某一维的变量小于此值时，令序列中的相应位置的整数为零，即消去对应的换热器。

3.2 整型变量进化策略

整型变量进化策略是对整型变量判断策略的进一步延伸和拓展。但从费用函数角度分析，过多的换热器是不利于费用值降低的，所以本文以整型变量判断策略为基础，提出了整型变量进化策略。即Powell粒子进行位置更新时，对其每一维所表示的换热器进行随机消去操作。详细操作如下：设定消去概率 pe，每一维变量进行更新时，产生随机数rand，当rand≤pe时，消去序列中整数表示的换热器。对于新产生的结构，本文通过构建一个接受概率函数pr，其形式如式（46）所示。

式中， Fold和Fnew分别为原结构和新结构对应的目标函数值，α=0.95为缩减因子，p0=0.2为pr的初始值。此处应注意的是，当换热器被消去后，若新结构的费用值降低，则此新解作为最佳的概率相应增大，种群中其他个体倾向于消去此换热器；若其费用值升高，则此新解作为最佳的概率相应减小，所以其他个体消去此换热器的概率也相应减少，而此个体在下次迭代过程中又可以通过学习其他个体，重生已消去的换热器。所以整型变量进化策略是一种以费用值为导向的进化策略，整型变量判断策略与其类似。

3.3 算法流程

Powell粒子群算法与整型变量优化策略相结合，能够实现换热网络的连续变量与整型变量的同步优化。其主要步骤为：随机生成 Np个 Powell粒子，包括初始位置向量Qn，0和速度向量V，其中，每个粒子均代表了一组潜在解。粒子在整个搜索空间内根据随机搜索特性、自身最优和邻居最优位置进行位置更新，同时执行整型变量优化策略，如图5所示。

图5 算法流程图

4 算例验证与分析

为验证Powell粒子群算法的性能，本文采取两个典型算例对其进行验证。计算环境为Win7系统下Fortran（Compaq Visual Fortran 6），计算机参数为Intel（R） Xeon（R） CPU E5-2670 v2 2.5GHz 32GB RAM。

4.1 算例一

算例一取自文献［15］，包含6股热流体与5股冷流体，算例的相关计算参数如表 1所示。CASTILLO 等［15］所得结构对应的费用值为141555$/a。SILVA 等［10］采用一种内、外层均为粒子群的双层算法同步综合换热网络，其获得的有分流分级超结构对应的年综合费用139777$/a。但在本文的计算中发现，在H4C3流股上的换热器的温度出现交叉，即热流体 H4的出口温度比冷流体 C3的入口温度低，如文献［10］中的图 6所示，因此认为他们的结构与费用值不符合，所以其计算结果不在本文的比较范围内。

表1 算例一参数

采用Powell粒子群算法优化算例一，得到图6所示的结构，变量单位为 kW，其费用值为140084$/a。通过分析表1中的数据可以发现，其热容流率数值差异很大，所以导致此算例的非线性很强，过程流体参数的细微改变，都会导致费用值的急剧变化。所得结果与文献的对比情况如表2所示，由其可知，两者的换热单元数与消耗的公用工程量近似相同，但根据参考文献［15］的结构发现，两者的换热网络结构并不同，即本文获得了优于文献的结果，证明了算法的高精度。

图6 算法优化结果（年综合费用：140084$/a）

表2 算例一结果比较

4.2 算例二

算例二取自文献［16］，是由 10股热流体与 10股冷流体组成大规模的换热网络问题，算例的相关参数如表3所示。XIAO等［16］采用一种传统的温焓图法设计多股流换热网络，其所得结果为1827772$/a。LUO 等［17］首次将此算例应用于两股流换热网络设计，并采用一种由遗传算法、模拟退火算法等组成的混合算法优化算例二，其获得的有分流分级超结构的费用值为1753271$/a。LAUKKANEN等［18］提出了一种对过程流体进行分组的双层算法来减少换热网络综合问题的复杂性，其获得的结构费用值为1811.9k$/a。

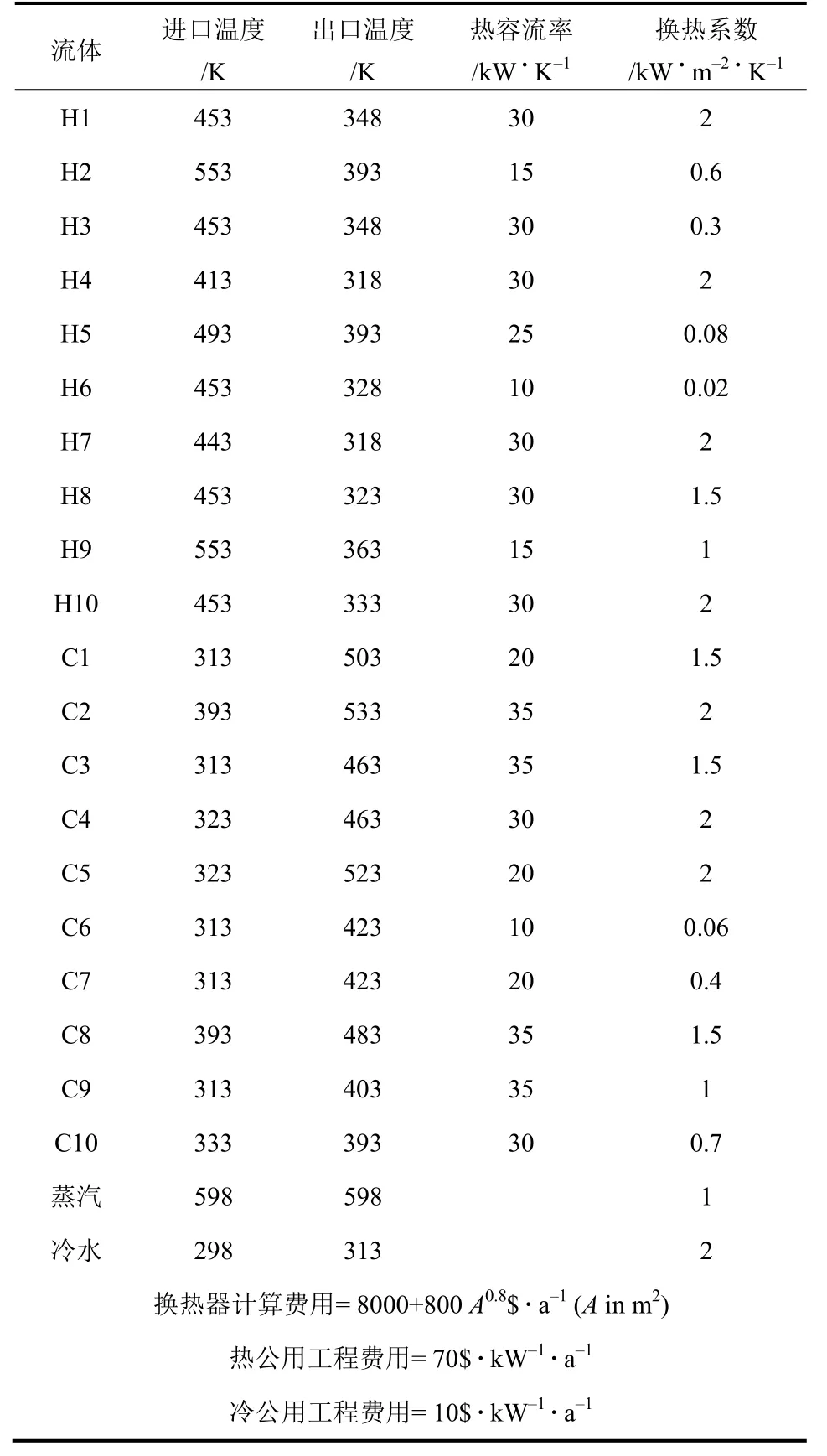
表3 算例二参数

采用Powell粒子群算法优化算例二，得到图7所示的结构，变量单位为 kW，其费用值为1745145$/a，与文献的结果对比如表4所示。可以发现，本文获得了相对于有分流分级超结构更优的结果，证明了算法处理大规模换热网络综合问题的高效性。计算时的相关参数如表5所示，所有的参数均为多次计算所取的经验值。

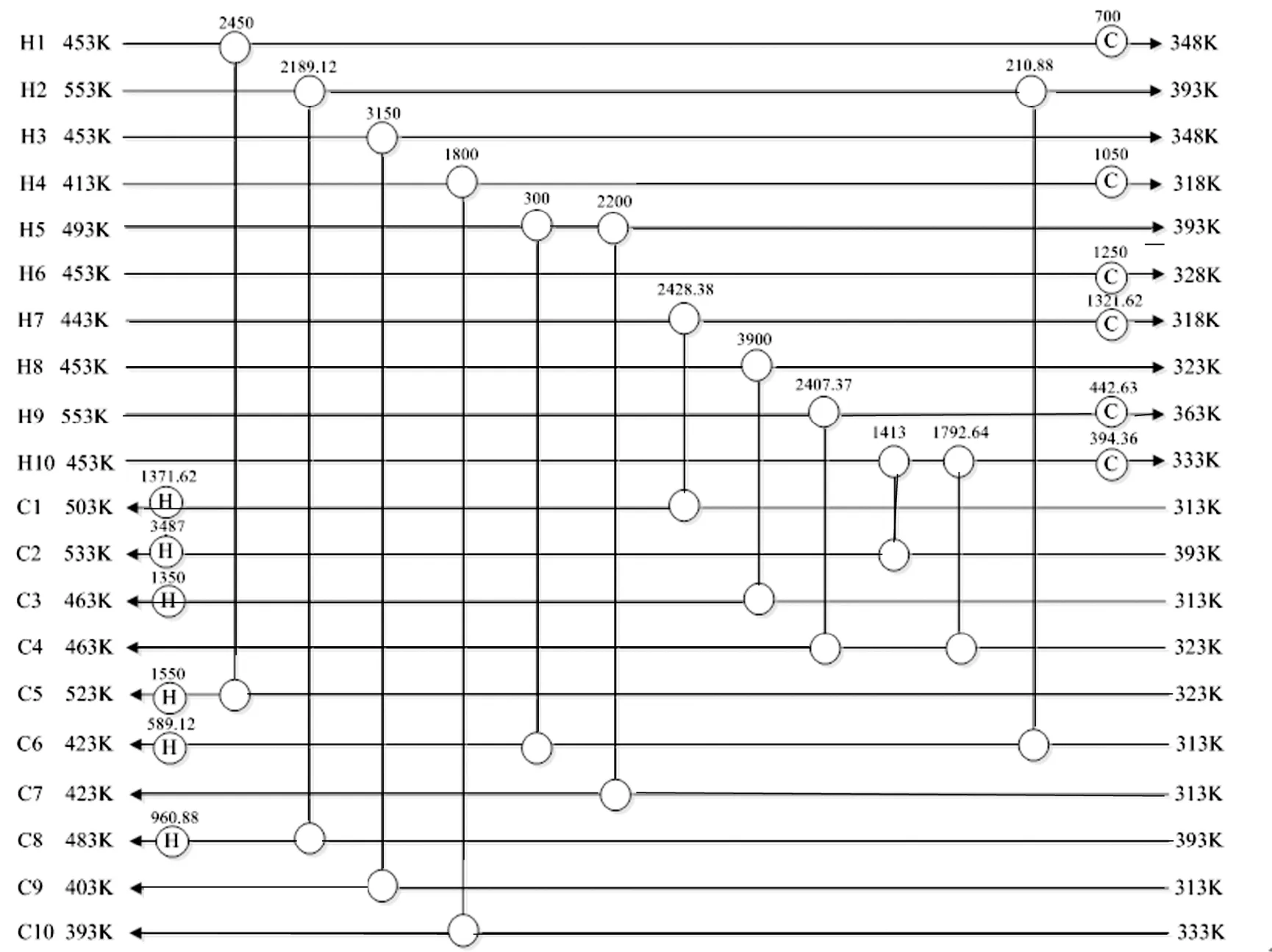
图7 算法优化结果（年综合费用：1745145$/a）

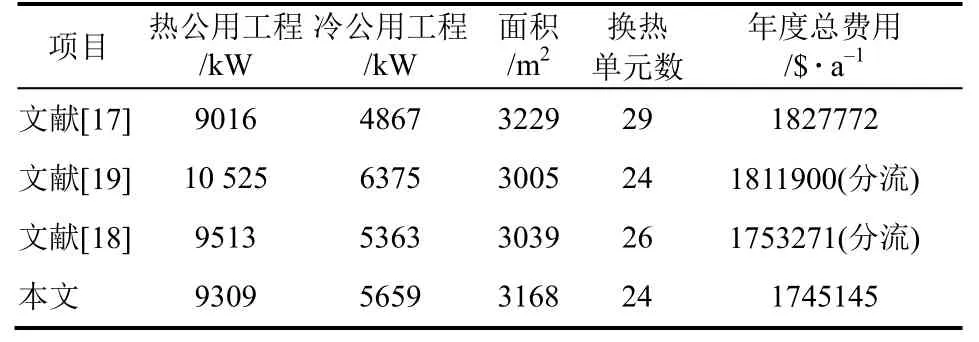
表4 算例二结果比较

表5 计算相关参数

5 结 论

本文提出了一种新型Powell粒子群算法，粒子的Powell特性使算法具有较高的搜索精度，而针对换热网络综合问题构建的启发式准则使算法具有较强的全局搜索能力，能够同时兼顾精度和效率。为优化换热网络结构而提出两条整型变量优化策略能够与Powell粒子群算法很好的契合，可以有效地处理问题中的整型变量。采用两个经典算例对算法进行验证，均获得了相对文献更优的结果，证明了算法的性能。

符 号 说 明

A——换热器面积，m2

B——取值为0或1的逻辑变量

C——费用计算系数

NC——冷流股数

NH——热流股数

NS——换热网络级数

NK——最大换热器数目

Np——种群个数

Q——换热器换热量，kW

V——粒子的速度

rand——取值介于（0，1）的随机数

T——温度，℃

Z——面积费用指数

上角标

in——换热器入口

out——换热器出口

下角标

c —— 冷流体

h —— 热流体

i —— 热流股标号

j —— 冷流股编号

k —— 级数编号

CU —— 冷公用工程

HU —— 热公用工程

［1］ FURMAN K C，SAHINIDIS N V. Computational complexity of heat exchanger network synthesis［J］. Computers & Chemical Engineering，2001，25（9）：1371-1390.

［2］ FURMAN K C，SAHINIDIS N V. A critical review and annotated bibliography for heat exchanger network synthesis in the 20th century［J］. Industrial & Engineering Chemistry Research，2002，41（10）：2335-2370.

［3］ LINNHOFF B，HINDMARSH E. The pinch design method for heat exchanger networks［J］. Chemical Engineering Science，1983，38（5）：745-763.

［4］ YEE T F，GROSSMANN I E. Simultaneous optimization models for heat integration——Ⅱ. Heat exchanger network synthesis［J］. Computers & Chemical Engineering，1990，14（10）：1165-1184.

［5］ CHOI S H，MANOUSIOUTHAKIS V. Global optimization methods for chemical process design：deterministic and stochastic approaches［J］. Korean Journal of Chemical Engineering，2002，19（2）：227-232.

［6］ GROSSMANN I E，SARGENT R W H. Optimum design of multipurpose chemical plants［J］. Industrial & Engineering Chemistry Process Design and Development，1979，18（2）：343-348.

［7］ ZAMORA J M，GROSSMANN I E. A global MINLP optimization algorithm for the synthesis of heat exchanger networks with no stream splits［J］. Computers & Chemical Engineering，1998，22（3）：367-384.

［8］ DIPAMA J，TEYSSEDOU A，SORIN M. Synthesis of heat exchanger networks using genetic algorithms ［J］. Applied Thermal Engineering， 2008，28（14）：1763-1773.

［9］ YERRAMSETTY K M，MURTY C V S. Synthesis of cost-optimal heat exchanger networks using differential evolution ［J］. Computers & Chemical Engineering，2008，32（8）：1861-1876.

［10］ SILVA A P，RAVAGNANI M A S S，BISCAIA Jr E C，et al. Optimal heat exchanger network synthesis using particle swarm optimization［J］. Optimization and Engineering，2010，11（3）：459-470.

［11］ 张安玲，王中. 一种混合粒子群优化算法的研究［J］. 计算机工程与应用，2011，47（31）：27-29.

［12］ 吴建辉，章兢，陈红安. 融合Powell搜索法的粒子群优化算法［J］.控制与决策，2012，27（3）：343-348，354.

［13］ 罗平，姚立海，杨仕友，等. 基于移动最小二乘法和粒子群算法的优化算法［J］. 浙江大学学报：工学版，2006，40（9）：1482-1485.

［14］ POWELL M J D. An efficient method for finding the minimum of a function of several variables without calculating derivatives ［J］. The Computer Journal，1964，7（2）：155-162.

［15］ CASTILLO E，ACEVEDO L，REVERBERI A P. Cleaner production of nitric acid by heat transfer optimization： a case study ［J］. Chemical and Biochemical Engineering Quarterly，1998，12（3）：157-165.

［16］ XIAO Wu，DONG Hongguang，LI Xinqing，et al. Synthesis of large-scale multistream heat exchanger networks based on stream pseudo temperature ［J］. Chinese Journal of Chemical Engineering， 2006，14（5）：574-583.

［17］ LUO X，WEN Q Y，FIEG G. A hybrid genetic algorithm for synthesis of heat exchanger networks ［J］. Computers & Chemical Engineering， 2009，33（6）：1169-1181.

［18］ LAUKKANEN T，FOGELHOLM C J. A bi-level optimization method for simultaneous synthesis of medium-scale heat exchanger networks based on grouping of process streams［J］. Computers & Chemical Engineering，2011，35（11）：2389-2400.

A novel Powell particle swarm optimization algorithm for simultaneous synthesis of heat exchanger networks

ZHANG Chunwei，CUI Guomin
（Research Institute of New Energy Science and Technology，University of Shanghai for Science and Technology，Shanghai 200093，China）

Due to the defect of simultaneous methods for heat exchanger networks synthesis，a novel Powell particle swarm optimization（PPSO） algorithm was proposed，which has both high precision of the deterministic methods and high efficiency of the stochastic algorithms. For overcoming disadvantages of stochastic algorithms，the cloud memory and the opposite strategy of individualswere proposed，which can avoid premature convergence and expand the search space. In addition，two optimizing strategies of integer variables were combined with PPSO algorithm in order to simultaneously optimize continuous and integer variables. The presented approach was tested on two typical benchmark problems. The obtained solutions are better than that published in the literature. Results showed that the presented algorithm can find better designs，which is conductive to cost saving in industrial production.

heat exchanger networks synthesis；integer variables；Powell method；swarm intelligence

TK 124

A

1000-6613（2016）10-3092-09

10.16085/j.issn.1000-6613.2016.10.012

2016-01-27；修改稿日期：2016-02-23。

国家自然科学基金项目（51176125）。

张春伟（1992—），男，硕士研究生，从事过程系统优化研究。联系人：崔国民，教授，博士生导师。E-mail cgm1226@163.com。