竖直上升气液泡状流数学模型封闭的研究

周强，郭晓峰，李军，王腾，陈彩霞

（华东理工大学资源与环境工程学院，煤气化及能源化工教育部重点实验室，上海 200237）

竖直上升气液泡状流数学模型封闭的研究

周强，郭晓峰，李军，王腾，陈彩霞

（华东理工大学资源与环境工程学院，煤气化及能源化工教育部重点实验室，上海 200237）

竖直上升管气液两相流广泛应用于相变传热、核反应堆等工业过程。本文以竖直上升气液两相流为研究对象，运用欧拉双流体模型，针对表观液速为0.45m/s、表观气速分别为0.015m/s和0.1m/s的泡状流数值模拟过程中的升力、壁面润滑力、湍流扩散力、气泡诱导湍流（BIT）等封闭模型，开展数值模拟比较研究。模拟发现：①低气速泡状流中，升力和壁面润滑力的同时加入能够改善壁面附近的气含率，气泡在这两个力作用下在径向上达到一个相对平衡，得到与实验气含率类似的壁面峰，模拟的液相速度较合理；低气速时，BIT的影响可以忽略。②高气速泡状流中，BIT对气-液两相流的模拟结果影响比较明显，湍动耗散源项的加入能使液速分布的模拟结果得到改善，Troshko模型相对Sato模型更能反映气泡诱导湍流对液相湍流的作用。③高气速时升力的引入使气含率产生壁面峰，加入湍流扩散力能使峰值略微降低，但仍没有解决高气速时引入升力出现的气含率壁面峰问题，说明在径向上湍流扩散力还不足以抵抗升力。

气-液两相流；泡状流；气泡诱导湍流；升力；壁面润滑力

气液两相流广泛应用于化学反应器、油气输运管道和核反应器等工业设备［1］。数值模拟是研究气液两相流体动力学的重要手段，其中，欧拉双流体模型是模拟气液两相流较为实用的方法。然而，求解气液两相守恒方程的数值封闭仍不成熟，已有的数值方法和封闭模型还存在一定的差异，这在很大程度上影响着CFD模型的通用性。

气泡所受的相间作用力直接决定了气泡的运动轨迹和气液间的相对速度，即控制了气泡的分布模式［2］。气液相间作用力包括曳力、升力、湍流扩散力、虚拟质量力等。早期的模拟研究多数只考虑气泡与液体之间的曳力作用而忽略其他相间作用力。TOMIYAMA等［3］通过单气泡在流场中的运动实验发现气泡的径向运动与气泡的尺寸有关；SHAWKAT［4］、LUCAS［5］、王晓冬［6］等发现随着表观液速与表观气速的比值增大，气含率峰值会逐渐由中心转到靠近壁面。OHNUKI等［7］认为湍流扩散力克服升力，两者相互作用决定气含率的径向分布；SHAWKAT等［4］进一步确认气含率分布取决于升力和湍流扩散力的方向和相对大小。孙波等［8］也发现升力和湍流扩散力的共同作用影响气泡的径向运动，但其中升力占主导，气泡尺寸超过临界尺寸5.7mm时升力方向发生改变，使气含率由壁面峰转为中心峰。李兆奇等［9］认为升力和湍流扩散力是鼓泡塔内气含率稳定分布的主要机制，他们引入湍流扩散经验系数，提出了基于径向力平衡的鼓泡塔二维流体力学模型，适合模拟大型鼓泡塔内不同表观气速条件下的气含率和液速分布。除了相间作用力，ANTAL［10］、TOMIYAMA［11］和 HOSOKAWA等［12］研究了气泡与壁面的相互作用，相继提出了不同的壁面润滑力模型。韩朋飞等［13］针对泡状流对几种壁面润滑力模型进行对比，发现相比其他几种模型，Hosokawa模型对气含率分布的预测更加合理。在气液两相流中，气泡作为诱导液相湍流的来源促使液相由层流向湍流转变［14］，气泡诱导湍流模型（BIT）主要包括气泡诱导湍流黏度型和曳力型-源项模型，这些模型的适用性未知。

本文对竖直上升管泡状流数值模拟过程中的不同封闭模型开展数值模拟研究，着重分析升力、湍流扩散力和壁面润滑力对竖直上升气液泡状流动的影响；比较不同气泡诱导湍流模型对液相湍流参数模拟结果影响，探讨模拟竖直上升气液泡状流动的数值封闭模型。

1 理论模型

1.1 双流体模型

在气液两相鼓泡流中，一般采用欧拉双流体模型；该方法假定液体为连续相，气体为不可压缩的拟流体，不考虑气液相间质量传递。具体的连续性方程和动量传递方程如式（1）、式（2）。

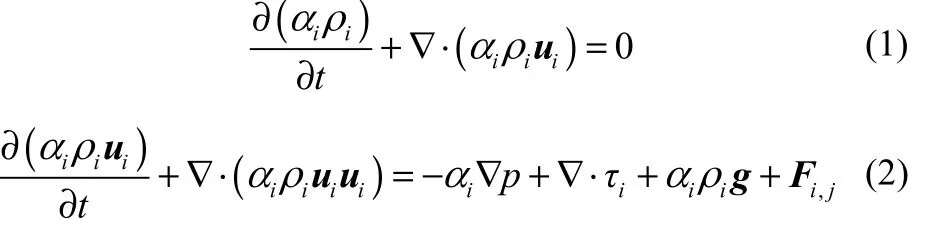
1.2 湍流模型

双流体模型中的运动方程进行雷诺时均化后，由湍流脉动引起的二阶和高阶项需要通过湍流方程封闭，其中最为重要的是湍流黏度μt的确定［15］。对于离散相相含率较低的流动，研究者普遍采用Standard k-ε模型对液相湍流进行描述，离散相湍流参数不是通过输运方程来获得，而是通过运动的时间尺度和长度尺度的代数关系估算。液相的k和ε通过式（3）、式（4）的输运方程来计算。

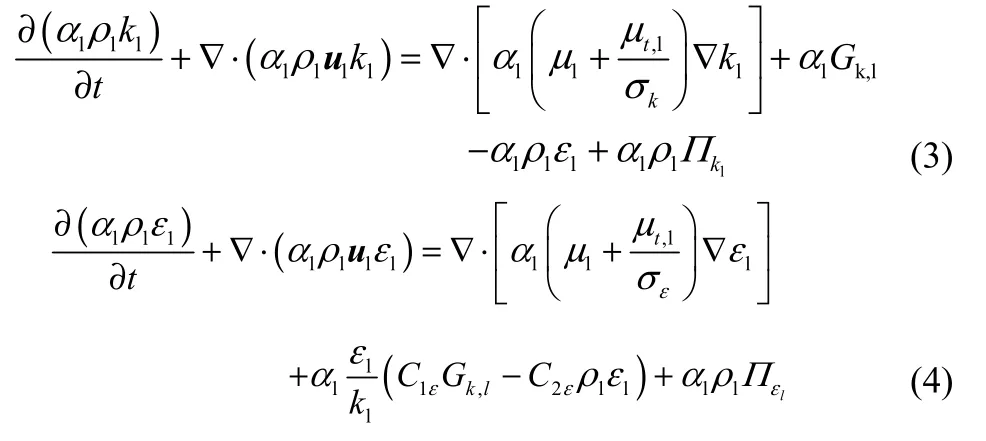
式中，Clε、C2ε和Cμ为经验常数，分别为1.44，1.92，0.09；σk、σε分别为与湍动能k和耗散率ε对应的Prandtl数；Gk，j为由于平均速度梯度引起的湍动能k的产生项，为用户自定义的源项，如气泡诱导湍流源项。

气泡诱导湍流（BIT）是指气泡尾涡产生的涡旋效应，即气泡的存在对液相湍流的影响。本文分别使用SATO和TROSHKO两种典型的BIT模型进行模拟对比。SATO等［16］认为气相的随机运动对液相的黏度产生影响，该模型对液相有效黏度进行调整，加入了由于气相存在对液相黏度的影响，见式（5）、式（6）。

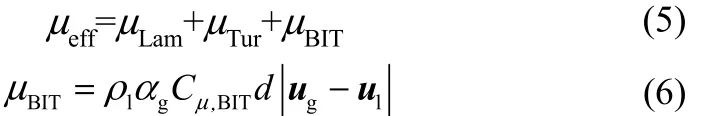
式中，μeff为有效黏度，由三部分构成，即μLam、μTur、μBIT分别为分子黏度、湍流黏度、气泡诱导湍流黏度增加项。Cμ，BIT默认为0.6。

TROSHKO等［17］模型将气泡受到曳力而损失的能量转化为气泡尾涡的湍动能，在湍流输运方程中添加源项，湍动能及耗散率的源项如式（7）～式（8）。

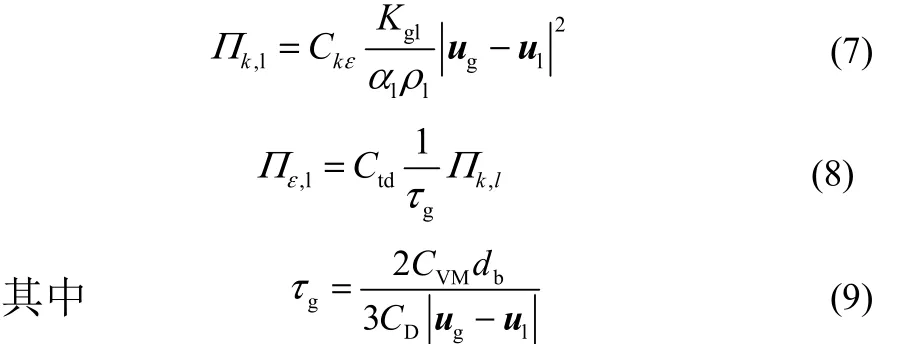
式中，Ckε、Ctd和τg分别是湍动源和耗散源的调整因子和特征时间尺度；CVM是虚拟质量力系数0.5；CD是曳力系数；Ckε、Ctd默认分别为0.75、0.45。

1.3 相间作用力模型

计算相间作用力需要使用气泡尺寸，早期的研究大多采用单尺寸气泡模型；对于高气速的气液两相流，XU［18］、李倩［19］等引入气泡合并分裂模型模拟气泡尺寸分布。本文研究的竖直上升管泡状流体系中，气速较低且气泡尺寸相对均一，不考虑气泡尺寸的分布，采用实验报道的单一尺寸气泡尺寸。

1.3.1 曳力

曳力为气泡与周围的流体发生相对运动而产生的相互作用力，可表示为式（10）。

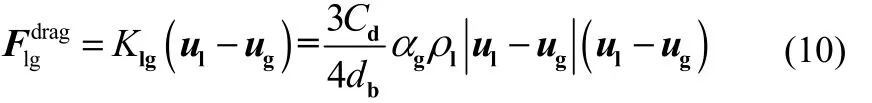
1.3.2 升力

气泡在剪切流中运动时会受到垂直于其运动方向的力，这种力称为剪切诱导升力。升力与气液相间相对速度和液相速度的旋度有关，见式（14）。

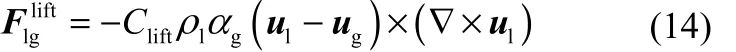
式中，Clift为升力系数。本文采用TOMIYAMA［3］升力模型，该模型中升力系数经FRANK等［21］改进后形式如式（15）～式（18）。

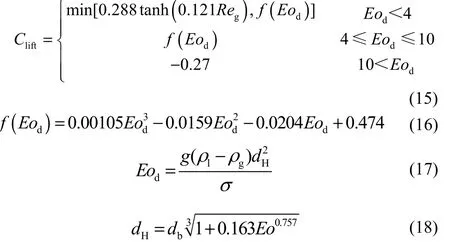
式中，dH为气泡的水平方向尺寸，通过类球形气泡的横纵比经验公式计算。

1.3.3 壁面润滑力

由于壁面的存在对离散相的作用称为壁面润滑力。对于管流，管壁附近的气泡及其分布对流型的影响不容忽视。壁面润滑力的形式如式（19）。

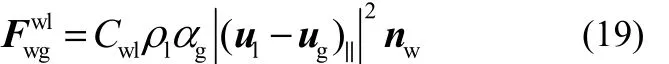
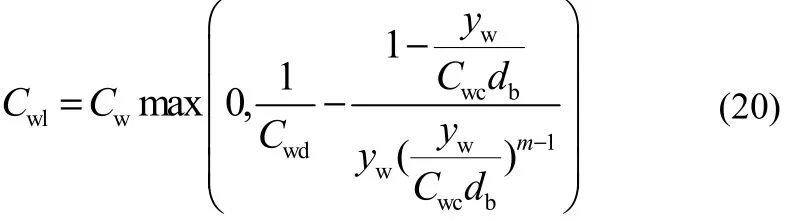
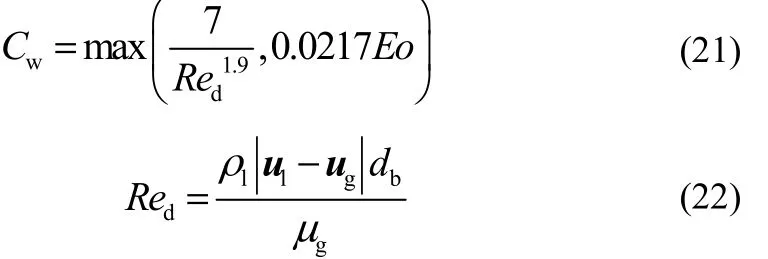
式中，Cwd为阻尼系数，用来衡量力的相对大小；yw为气泡离壁面的最小距离；Cwc为截断系数，用来衡量壁面润滑力的作用范围；Cwd、Cwc、m默认分别为6.8、10、1.7。

1.3.4 湍流扩散力

湍流扩散力源于气液相湍流脉动。气液两相曳力可以分为平均和脉动两部分，其中平均部分由曳力考虑，脉动部分由BURNS等［22］基于Favre平均推导，形式如式（23）。

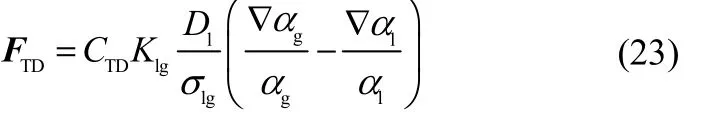
式中，CTD、σlg为常数，分别为1和0.9；Klg为界面交换系数；Dl为湍流扩散系数，表示如式（24）。

2 结果分析与讨论

2.1 数值模拟方法与操作条件

本次模拟基于SHAWKAT等［4］实验。该实验中，竖直管的高度和直径分别为9.56m和0.2m。表观液速恒定为0.45m/s，表观气速为0.015m/s、0.1m/s。实验数据全部在高度 8.4m处采集，气含率通过双光学探针测定，轴向液速通过TSI 1210-60W的热膜探针测定。模拟采用的气泡尺寸为实验测得气泡尺寸平均值，见表1。

表1 进口条件及气泡尺寸

模拟借助ANSYS Fluent 15.0软件［23］，动量和体积分数均采用QUICK离散格式，其他离散方程均采用二阶迎风格式。液态水作为连续相、常温常压的空气作为拟流体。初始时管内充满水，底部进口设为速度边界，上部出口采用压力边界。壁面液相设定为无滑移、气相为自由滑移，非稳态计算时间步长为0.01s，待液面达到稳定后继续计算并进行50s时间平均。对比了两种规模的网格确定网格无关性，方案1：网格总数为219790，网格平均尺寸Δx=Δy≈7.1mm，Δz≈29.9mm。方案 2：网格总数为339735，网格平均尺寸Δx=Δy≈4.7mm，Δz保持不变，横截面网格如图1所示。

图2即为上述两种不同网格模拟得到的气含率结果，可以看出网格Ⅰ和网格Ⅱ得到的气含率没有明显区别，壁面峰径向位置几乎重合，所以在后面的工作中，统一采用方案1的网格。

图1 横截面网格划分

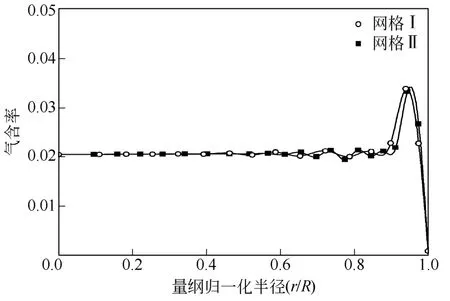
图2 网格对气含率模拟结果的影响

2.2 径向力对流场的影响

如图3所示，加入Tomiyama升力模型后，由于4.1mm气泡所受的升力方向指向壁面，导致壁面附近气含率上升。如果没有壁面润滑力，壁面上的气含率最大，这与实际不符。低气速实验得到的气含率分布之所以出现壁面峰，是因为气泡受到的径向力在壁面附近处于一个平衡状态，而壁面附近气含率受壁面润滑力的直接影响，如图3（a）所示，在升力的作用基础上，加入Hosokawa壁面润滑力模型之后，气含率出现壁面峰，相比不加壁面润滑力有很大改善。虽然相比实验壁面峰的径向位置仍然有所偏移，但是能够捕捉到壁面峰值。因此，对于低气速的情况，壁面润滑力的作用比较重要。同时，由图3（b）所示，在升力和壁面润滑力的共同作用下，气泡的径向湍动增强，由能量守恒可得，轴向湍动必然减弱，所以中心区域轴向液速相比不加升力时有所降低，与实验值吻合较好。

接下来为了验证本文采用单尺寸气泡模型而忽略气泡的合并分裂的合理性，对比了不同轴向高度处的气含率及轴向液速，如图 4所示。表观气速0.015m/s时不同轴向高度处的气含率的径向分布几乎重合，轴向液速大小也比较接近，说明流场中气液两相流动较为稳定，不存在剧烈的湍动，所以采用单尺寸气泡模型满足计算的要求。

在气相驱动液相的鼓泡流中，不同时刻流场内波动较为明显，流动处于非稳态；本文所计算的竖直上升管内气液两相并流上升，因为以上两种流动动力驱动本质的不同，流动的稳定性可能也有所差异。图5对比了表观气速0.015m/s时流动达到相对稳定后 8.4m高度处不同时刻的瞬时轴向液速，虽然是瞬时结果，但是3个时刻的轴向液速径向分布没有明显波动，并且液速大小也比较接近，说明在气液并流的竖直上升流中，流动比较容易达到相对稳定状态，且不同时刻的液速值存在些许差异，说明本文采用50s时间平均结果较为合理。

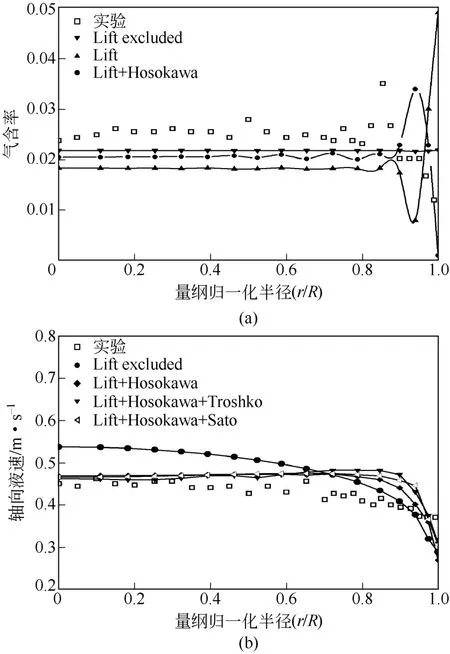
图3 表观气速0.015m/s时径向力对气含率的影响以及径向力和不同BIT对轴向液速的影响

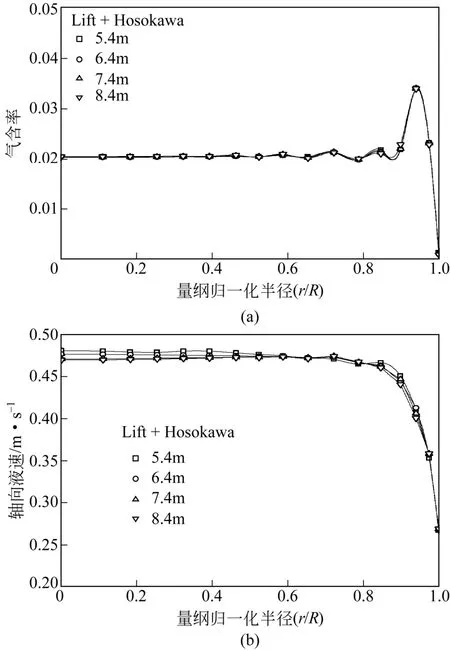
图4 表观气速0.015m/s时不同轴向高度处气含率分布以及轴向液速

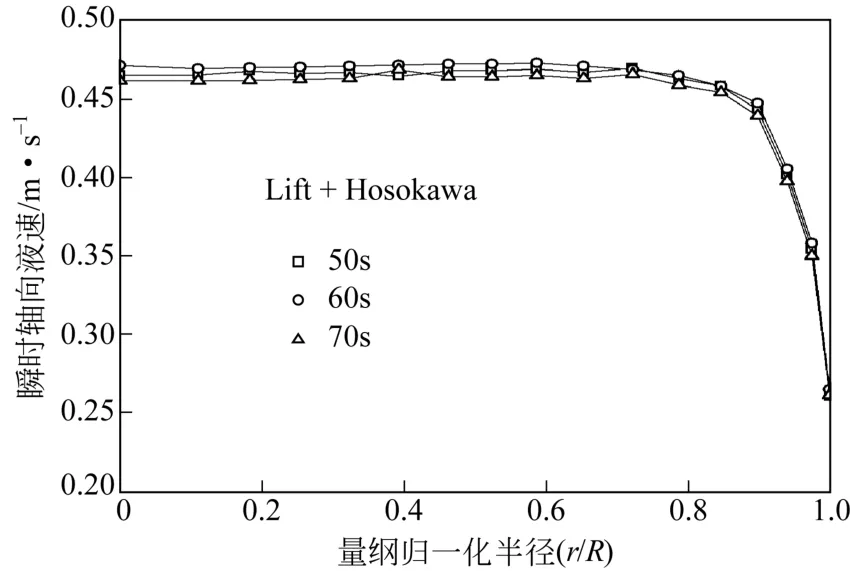
图5 表观气速0.015m/s时不同时刻瞬时轴向液速

图6（a）、（b）分别为表观气速0.1m/s时气含率及轴向液速的径向分布。对于尺寸为 5mm的气泡，使用Tomiyama升力模型，气泡受到的升力总体方向仍指向壁面，由图 6（a）可以明显看出，加入升力后壁面附近气含率陡升，同时由于壁面附近大量气泡的带动，使得壁面附近的液速有明显的提升，而中心区域的液速比较平坦，模拟结果不尽合理；同时考虑升力和壁面润滑力后，气含率分布并没有得到改善，同样出现与低表观气速时类似的壁面峰；进一步分析发现加入 Burns湍流扩散力模型，预测气含率的壁面峰值略微降低，轴向液速的壁面峰变得平滑，虽然液速有所好转，如果同时加入升力仍然出现壁面峰，说明湍流扩散力在径向上不足以平衡升力的作用；当不考虑升力时，壁面附近气含率反而显得更为合理，轴向液速有所提升，但是与实验值比较，中心区域的液速仍然偏低。

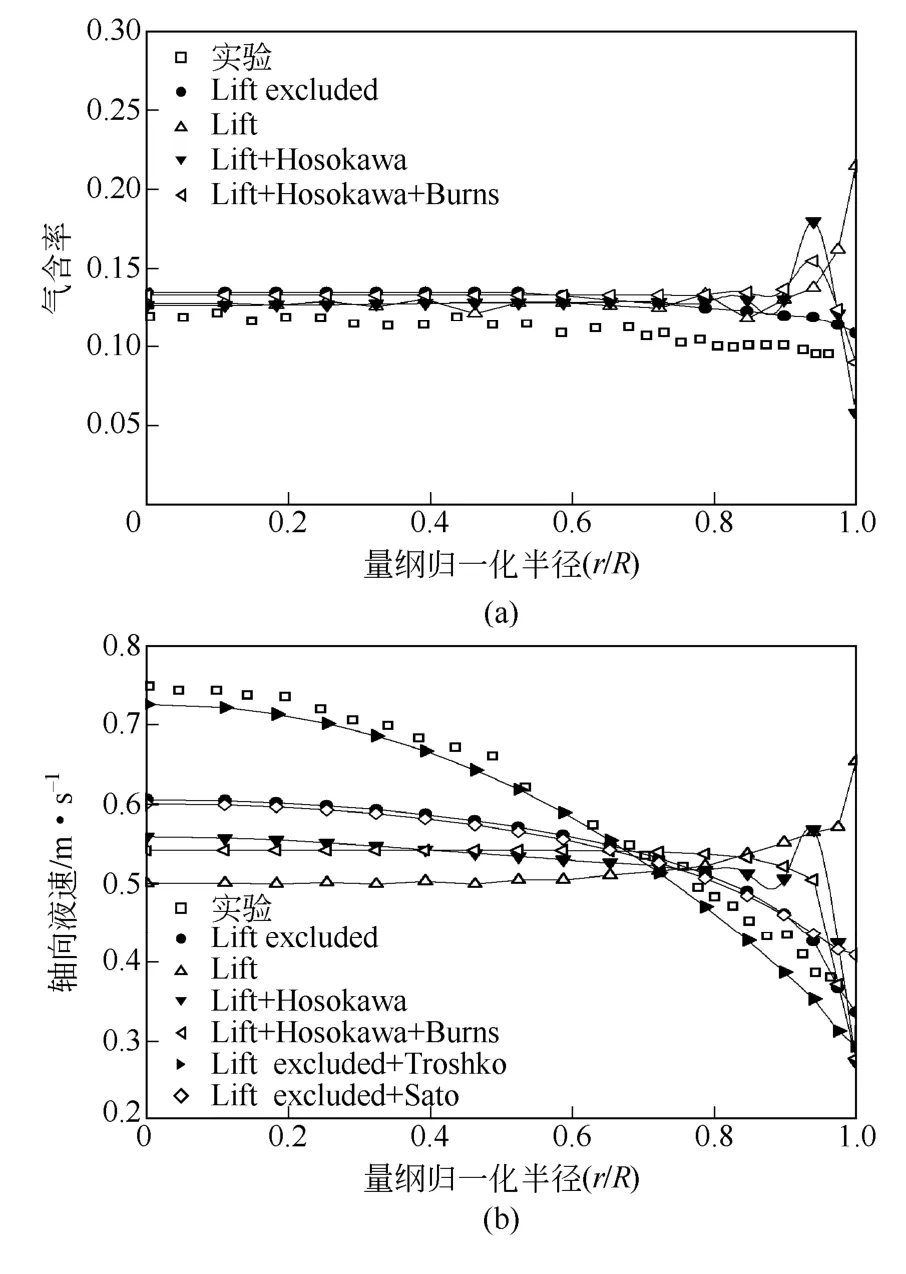
图6 表观气速0.1m/s时径向力对气含率的影响以及径向力和不同BIT对轴向液速的影响

在高气速泡状流模拟时加入升力所得结果之所以不尽合理，是因为高气速时湍流更加强烈，导致气泡合并与分裂及尺寸分布更广，而本模拟使用单尺寸气泡模型，根据TOMIYAMA的升力模型［11］，不同尺寸的气泡的升力作用方向不同，较大尺寸气泡 所受升力方向指向中心，较小气泡的升力指向壁面。因此今后在高气速竖直上升气液两相流研究中有必要引入气泡合并分裂模型。

2.3 BIT模型对流场的影响

BIT模型的主要作用是增强液相的湍动。不同BIT模型对湍流参数的影响见图7。由图3（b）可知，表观气速0.015m/s时，加入BIT对轴向液速影响很小，仅在壁面附近液速略微提升，由此可见低气速时气泡诱导湍流对液相的湍动作用微弱，此时BIT对液相速度的影响可以忽略。

图6（b）对比了表观气速0.1m/s时两种BIT模型对轴向液速的影响，加入Troshko模型后中心区域轴向液速明显提升，计算值与实验值吻合较好。而Sato模型对液相速度的影响并不显著，中心区域液速与不加BIT模型几乎重合，仅在壁面附近液速略有提升。这是因为，气泡受到曳力的作用，损失了一部分能量，以往很少考虑这部分能量对流场的影响，而在BIT模型中，认为这部分损失的能量全部转移到气泡的尾涡中，从而增强了液相的湍动，故在高气速时应该考虑BIT对液相湍动的影响。

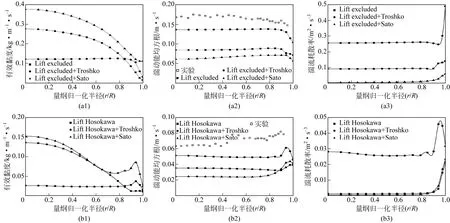
图7 不同BIT模型对湍流参数的影响

Sato模型的作用机理与Troshko模型不同。Sato模型修改了有效黏度项，认为气相的存在间接地增加了液相的有效黏度。从图7（a）可以看出，加入了Sato模型后，液相有效黏度有所增加，因为有效黏度制约了涡的耗散，所以耗散率有所减弱，同时湍动能也随之降低；相反，Troshko模型在湍流输运方程中加入源项，得到的最终湍流黏度降低，而湍动能和耗散率明显升高，湍动能更加接近实验结果，并且从轴向液速与实验值对比结果可以看出，Troshko模型相比Sato模型在增强液相湍动上有明显的优势。图 7（b）为0.015m/s表观气速时的湍流黏度、湍动能和耗散率分布，三者分布与高气速时趋势相同，并且在加入Troshko模型之后，壁面附近的湍流黏度、湍动能和耗散率出现与气含率类似的壁面峰情况，而此现象正是由气含率的壁面峰造成的。

以上结果表明，无论是在低气速还是高气速下，Troshko模型都增强了涡的耗散。在多尺寸气泡模型（PBM）中，气泡的分裂速度与流场内的耗散率有关，耗散率越大，气泡分裂速度越快，所以以Troshko模型为代表的气泡诱导湍流能够促进气泡的分裂，这些结果为今后进一步导入 PBM模型提供了重要参考。

3 结 论

（1）低气速泡状流中，升力和壁面润滑力的同时加入能够改善壁面附近的气含率，气泡在这两个力作用下在径向上达到一个相对平衡，得到与实验气含率类似的壁面峰，并且液相速度也得以改善；低气速时，由于系统中气含率较低，气相对液相的湍动贡献较小，BIT的影响基本上可以忽略。

（2）高气速泡状流中，BIT对气-液两相流的模拟结果影响比较明显，由于湍动耗散源项的加入，使得液速分布得到改善，Troshko模型相对Sato模型更能反映气泡诱导湍流对液相湍动的作用，其中，高气速时BIT的影响比较显著。

（3）高气速时，湍流扩散力的加入使峰值稍有降低，液速壁面附近的小尖峰变得平坦，但总体上仍没有明显改善，说明对于 5mm的气泡，湍流扩散力还不足以在径向上平衡升力的作用；在模拟高气速竖直上升气液两相流时有必要引入气泡合并分裂模型，此时升力的作用更加显著。

符 号 说 明

Cd—— 曳力系数

Clift—— 升力系数

Cwl—— 壁面润滑系数

Dl—— 耗散标量，m2/s

d—— 气泡直径，m

Eo—— Eötvös数

Flg—— 相间动量交换项，N/m3

FTD—— 湍流扩散力，N/m3

Fwl—— 壁面润滑力，N/m3

Gk，l—— 湍动能产生项，w/m3

Re—— 雷诺数

u—— 速度矢量，m/s

ub—— 气泡速度，m/s

Ug—— 表观气速，m/s

α —— 体积分数

ε—— 湍动耗散率，m2/s3

k—— 湍动能，m2/s2

μ—— 动力黏度，kg/（m·s）

μBIT—— 气泡诱导湍流黏度，kg/（m·s）

μLam—— 分子黏度，kg/（m·s）

μTur—— 湍流黏度，kg/（m·s）

Πε，l—— 气泡诱导湍流扩散率源项，W（s·m3）

Πk，l—— 气泡诱导湍流源项，W/m3

ρ—— 密度，kg/m3

σ—— 表面张力，kg/m2

τ—— 应力，kg/m3

τg—— 特征时间尺度，s

下角标

b—— 气泡

g—— 气相

l—— 液相

i，j—— 相标，数标

［1］ LIAO Y，LUCAS D. Investigations on bubble-induced turbulence modeling for vertical pipe bubbly flows［C］// 2012 20th International Conference on Nuclear Engineering and the ASME 2012 Power Conference. American Society of Mechanical Engineers，2012：519-527.

［2］ 庞明军，徐一丹，魏进家. 管道泡状流相分布模式和分布机理研究进展［J］. 化工进展，2014，33（11）：2829-2842.

［3］ TOMIYAMA A，TAMAI H，ZUN I，et al. Transverse migration of single bubbles in simple shear flows［J］. Chem. Eng. Sci.，2002，57：1849-1858.

［4］ SHAWKAT M E，Ching C Y，Shoukri M. Bubble and liquid turbulence characteristics of bubbly flow in a large diameter vertical pipe［J］. International Journal of Multiphase Flow，2008，34（8）：767-785.

［5］ LUCAS D，KREPPER E，PRASSER H M. Prediction of radial gas profiles in vertical pipe flow on the basis of bubble size distribution［J］. International Journal of Thermal Sciences，2001，40（3）：217-225.

［6］ 王晓冬，张孜博，屠基元. 垂直上升圆管内等温泡状流的数值模拟［J］. 力学学报，2008，40（4）：441-446.

［7］ OHNUKI A，AKIMOTO H. Experimental study on transition of flow pattern and phase distribution in upward air-water two-phase flow along a large vertical pipe［J］. International journal of multiphase flow，2000，26（3）：367-386.

［8］ 孙波，孙立成，幸奠川，等. 竖直大圆管内两相流界面分布机理［J］.化工学报，2012，63（12）：3812-3817.

［9］ 李兆奇，王丽军，管小平，等. 基于径向力平衡的鼓泡塔二维流体力学模型［J］. 化工学报，2014，65（11）：4222-4230.

［10］ ANTAL S P，LAHEY R T，FLAHERTY J E. Analysis of phase distribution in fully developed laminar bubbly two-phase flow［J］. International Journal of Multiphase Flow，1991，17（5）： 635-652.

［11］ TOMIYAMA A. Struggle with computational bubble dynamics［J］. Multiphase Science and Technology，1998，10（4）：369-405.

［12］ HOSOKAWA S，TOMIYAMA A，MISAKI S，et al. Lateral migration of single bubbles due to the presence of wall［C］//ASME 2002 Joint US-European Fluids Engineering Division Conference. American Society of Mechanical Engineers，2002：855-860.

［13］ 韩朋飞，郭烈锦，程兵. 泡状流三维模拟及壁面润滑力模型比较［J］.工程热物理学报，2014（10）：1979-1983.

［14］ HOSOKAWA S，TOMIYAMA A. Bubble-induced pseudo turbulence in laminar pipe flows［J］. International Journal of Heat and Fluid Flow，2013，40：97-105.

［15］ 李希，李兆奇，管小平，等. 气液鼓泡塔流体力学研究进展［J］. 高校化学工程学报，2015，29（4）：765-779.

［16］ SATO Y，Sekoguchi K. Liquid velocity distribution in two-phase bubble flow［J］. International Journal of Multiphase Flow，1975，2（1）：79-95.

［17］ TROSHKO A A，HASSAN Y A. A two-equation turbulence model of turbulent bubbly flows［J］. International Journal of Multiphase Flow， 2001，27（11）：1965-2000.

［18］ XU L，YUAN B，NI H，et al. Numerical simulation of bubble column flows in churn-turbulent regime：comparison of bubble size models［J］. Ind. Eng. Chem. Res.，2013，52（20）：6794-6802.

［19］ 李倩，程景才，杨超，等. 群体平衡方程在搅拌反应器模拟中的应用［J］. 化工学报，2014，65（5）：1607-1615.

［20］ ISHII M，ZUBER N. Drag coefficient and relative velocity in bubbly，droplet or particulate flows［J］. AIChE J.，1979，25（5）：843-855.

［21］ FRANK T，SHI J，BURNS A D. Validation of Eulerian multiphase flow models for nuclear safety application［C］// Proceeding of the Third International Symposium on Two-Phase Modelling and Experimentation，Pisa，Italy. 2004.

［22］ BURNS A D，FRANK T，HAMILL I，et al. The Favre averaged drag model for turbulent dispersion in Eulerian multi-phase flows［C］// 5th International Conference on Multiphase Flow，ICMF，2004，4：1-17.

［23］ ANSYS Inc.. ANSYS FLUENT-15.0 Theory Guide ［M］. 2013.

·产品信息·

浙江力普短纤维粉碎机获国家专利

日前，中国粉碎技术领航者——浙江力普粉碎设备有限公司研发的“一种短纤维粉碎机”获得国家专利（专利号ZL. 2012 2 0434032.9）。

该项目已成为国家《产业结构调整指导目录》（2013修订本）优先支持发展的鼓励类领域。

据悉，目前国内用于粉碎短纤维性物料的粉碎设备以气流涡旋微粉磨为主，通过高速旋转的安装于转盘上的磨块与带齿定子间的气流碰撞，达到粉碎纤维的目的，对于短纤维的针对性不强，并且生产过程温升较高、能耗高、噪声大，物料粉碎后的粒度一般不超过80目，产量低，已不适应目前在新型材料、化工、医药、食品等领域对纤维粒度的产量的要求。

为改变这种状况，作为中国纤维素行业协会会员单位，浙江力普进行了一系列的创新开发，使专利产品可通过调节刀盘上的刀片与齿形内衬板之间的间隙调节产品的细度，也可通过调节转子的转速、分级盘上分级棒的数量来控制产品的细度及产量。从而实现了针对短纤维物料粉碎具有剪切作用效率高，单位能耗小，具有优异的节能减排效果；同时由于气流的高频振动打散物料具备一定的干燥效果，可有效降低物料含水量，降低湿度。

目前，该专利产品与浙江力普生产的精制棉粉碎机、纤维素成品粉碎机及湿粉碎机一起，在纤维素行业中得以广泛应用，客户包含国内规模前十位的纤维素醚生产企业并获得高度认可。

浙江力普咨询热线：13806745288、13606577969

传真：0575-83152666

力普网站：www.zjleap.com E-mail：zjleap@163.com

Comparative investigation on closure models for the simulation of vertical gas-liquid bubbly upflow

ZHOU Qiang，GUO Xiaofeng，LI Jun，WANG Teng，CHEN Caixia
（Key Laboratory of Coal Gasification and Energy Chemical Engineering of Ministry of Education，School of Resource and Environmental Engineering，East China University of Science and Technology，Shanghai 200237，China）

Gas-liquid upflow in vertical pipes was widely used in the phase change heat transfer and nuclear reactors. In this paper，the Euler-Euler two-fluid model was applied in the simulation of the gas-liquid upflow with the emphasis on the selections of the closure models. The lift force，wall lubrication force，turbulent dispersion force and bubble induced turbulence（BIT） were studied at a superficial liquid velocity 0.45m/s and superficial gas velocities，0.015m/s and 0.1m/s，respectively. The simulation results showed that：①At low superficial gas velocity，the near wall gas holdup can be optimized with both the lift force and wall lubrication force taken into account. The bubbles reached a relative balance under the effect of this two forces with the result of wall peak of gas fraction and the reasonable simulated liquid velocity；The effect of BIT can be negligible at low superficial gas velocity.②At high superficial gas velocity bubbly flows，the influence of BIT on the simulation results of gas-liquid two phase flow was evident. The simulation results can be improved with the turbulence dissipation source term included，and Troshko model prevailed over Sato model in describing the effect of bubble induced turbulence on the liquid turbulence. ③At high superficial gas velocity，the wallpeak of gas holdup occurred with the lift force included，then the peak value can be reduced after the turbulent dispersion force taken into account. While the issue of wall peak still can't be solved，indicating that turbulence dispersion force was not strong enough to overcome the lift force.

gas-liquid two phase flow；bubbly flow；bubble induced turbulence（BIT）；lift force；wall lu bricatio n force

O 359.1

A

1000-6613（2016）10-3049-08

10.16085/j.issn.1000-6613.2016.10.006

2016-03-11；修改稿日期：2016-05-13。

国家自然科学基金项目（21276085）。

周强（1991—），男，硕士，研究方向为多相流模拟。

联系人：陈彩霞，教授，博士生导师，研究方向为多相流体力学。E-mail cxchen@ecust.edu.cn。