受滑动平均有色噪声干扰的非均匀采样非线性系统的辨识算法研究

李向丽，夏静，陈维

（常熟理工学院电气与自动化工程学院，江苏常熟215500）

受滑动平均有色噪声干扰的非均匀采样非线性系统的辨识算法研究

李向丽，夏静，陈维

（常熟理工学院电气与自动化工程学院，江苏常熟215500）

研究受滑动平均有色噪声干扰的非均匀采样非线性系统的参数辨识算法.针对系统中存在不可测中间变量的问题，利用辅助模型对其进行估计，进一步提出递推增广最小二乘算法对系统参数进行辨识.并通过计算机MATLAB仿真验证了算法的有效性.

非线性系统；非均匀采样；辅助模型；滑动平均

1　引言

精确的数学模型对于实际工程系统的分析和控制至关重要，如果能够建立较为精确的数学模型，控制设计问题也能够迎刃而解［1］.传统的机理模型不能适应环境的变化和影响，建模精度偏低，而且现有的机理模型也存在着形式复杂、计算实时性不能保证等问题.因此，近年来对工业过程建模的研究主要集中在测试法建模（黑箱建模）上，而辨识技术则一直是测试法建模的研究热点.在现代工业中由于对经济效益、产品质量以及环境保护的要求越来越高，使得相应的工业过程越来越复杂，对模型的描述能力也提出了更高的要求.传统的线性模型已不能满足工业实际的需要，因此建立描述非线性现象的非线性系统，并深入研究非线性系统的辨识方法是十分必要的［2］.

目前，常见的非线性系统模型有：Volterra级数、块结构化非线性模型等［3］.基于模块化结构的非线性模型由一个动态的线性子模型和一个静态非线性子模型级联而成，具有能较好地反应非线性特性、计算量少、易辨识等特点，是近年来非线性动态建模和辨识研究的热点［2］.在20世纪60年代Narendra和Gallman提出了Hammerstein模型［4，5］，它由一个静态非线性子模型和一个动态线性子模型串联构成，可表征大部分非线性系统.关于Hammerstein模型的辨识，很多研究假设非线性子模型是不连续非线性［6］，或是一个两阶段或多阶段折线非线性［7，8］，还有一些方法假设非线性子模型是已知非线性基的线性组合［9］.在辨识方法上，Ding等提出了这类非线性系统的牛顿迭代辨识方法和牛顿递推辨识方法［10］；Vanbeylen和Pintelon等提出了极大似然盲辨识方法［11］；Wang等讨论了多新息增广最小二乘算法［12］和广义递推最小二乘算法［13］；Bai等推导了盲辨识法［14］；Goethals提出子空间辨识方法［15］；李秀英等把神经网络、遗传算法等应用到非线性系统辨识中［16］；王峰等利用改进的粒子群优化算法对Hammerstein模型进行参数辨识［17］.

在实际工业过程中，由于信息传输过程中存储数据硬件的损坏、数据的丢失、工作人员的变动、采样地点的改变、气候环境对采样数据的影响等都会导致数据采样的非均匀性，所以绝对的均匀采样非线性系统是不存在的，相对的非均匀采样非线性系统却是广泛存在的.当非线性系统的输入或者输出以非均匀间隔刷新，得到非均匀采样系统.Yamamoto等研究了双采样率线性系统的频域模型［18］；Lu和Fisher利用最小二乘算法和投影算法辨识双采样率模型的参数［19］；文献［20］利用提升技术处理非均匀采样数据，得到状态空间模型；Liu等采用递阶辨识的思想，将非均匀采样系统分解为多个辨识子系统，运用递推最小二乘算法辨识系统参数［21］.

本文研究受有色噪声干扰的非均匀采样非线性系统的参数辨识算法.当被控对象的干扰是有色噪声时，其信息矩阵中包含不可测噪声变量，首先通过建立辅助模型，利用输入输出数据估计这些未知变量的估计值，能够得到可估计的信息矩阵.然后提出递推增广最小二乘算法，得到系统的参数估计.最后利用仿真实例分析算法的性能和有效性.

2　非均匀采样非线性系统描述

下面是受滑动平均有色噪声干扰的非均匀采样非线性系统的描述.

首先利用周期为τ的零阶保持器Hr处理多采样率输入离散信号u（kT+t1）得到u（t）；u（t）作为非线性系统的输入，非线性系统由非线性子模型f（·）和线性子模型Pc级联形成，则分别得到非线性子模型的输出u-（t）和系统的真实输出y（t），但y（t）值不可测量；系统的真实输出y（t）经过周期为T的输出采样器ST，产生离散信号y（kT）；y（kT）是系统的输出采样，受噪声ω（kT）干扰后得到系统的可测输出ym（kT）.假设输入u（t）具有非均匀采样间隔，则经过零阶保持器后，输入u（t）可表示为：

这里框架周期T:=τ1+τ2+…+τr.假设非线性子模型的输出u-（t）为非线性基函数f:=（f1，f2…fn）的线性组合，

式中x（t）∈ℝnr是状态向量，u-（t）和y（t）是输入变量和输出变量，Ac、Bc、C、D是维数适当的矩阵.用框架周期T离散化（3）得到，

在采样时刻t=kT时，输出可表示为：

有色噪声输出ω（kT）被表示为ω（kT）=H（z）ν（kT），其中，

由系统图可知，

进一步，由式（4）和式（5），得到

根据上述参数的定义，等式（8）可改写为

将式（9）代入式（7），则系统输出ym（kT）可表示为

式（10）可等价的表示为

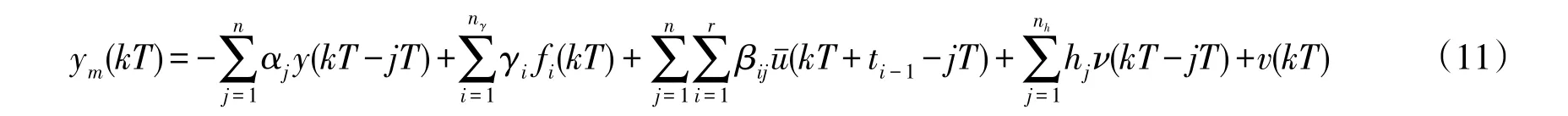
如果将非线性子模型代入式（11）就会产生一个包含参数乘积的表达式，虽然可以用过参数的方法进行化简［10］，但过参数化处理后会使待辨识参数增加，增加了算法的复杂性.关键项分离技术（key termseparation technique）［5］由Vörös教授首先提出，能够解决模型耦合的难题.把作为关键项，令β10=1，则可以把非线性系统的参数从线性动态系统中分解出来.得到如下滑动平均噪声干扰的非均匀采样非线性系统辨识模型：

3　递推增广最小二乘参数估计方法

针对受滑动平均有色噪声干扰的非均匀采样非线性系统，应用基于辅助模型的递推增广最小二乘算法估计模型参数，基本思想是借助一个参考模型（也称为辅助模型），用参考模型的输出估计代替系统不可测的变量，使得参考模型的输出逼近这些不可测的输出，从而获得系统参数的一致估计.再利用辅助模型的输出代替系统的不可测变量，进一步利用递推增广最小二乘算法得到系统的参数估计.

定义信息向量φ（kT）和参数向量θ如下：

式（12）可以写成向量形式：

式ω（KT）=H（Z）v（KT）也可以写成如下的向量形式：

定义二次准则函数，

注意到在式（16）和（17）中的信息向量φ（KT）包含未知内部变量，同时噪声也是未知的，因此参数向量θ通过最小二乘算法很难被估计.基于辅助变量思想，用估计

代替φ（KT）中的不可测变量y（KT）；用估计y（KT）代替式（2）中的γi进一步计算得到的估计

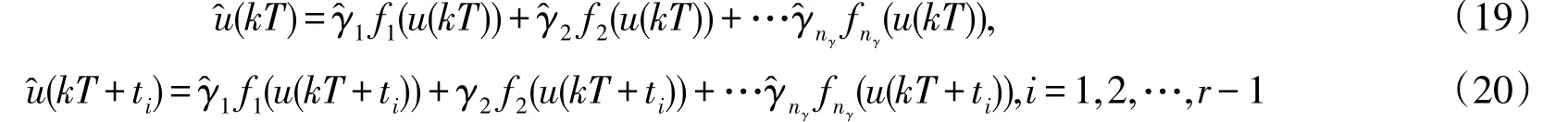
根据式（13）得到噪声的估计

进一步根据式（14）可以得到滑动平均噪声的估计

定义φ（KT）的估计

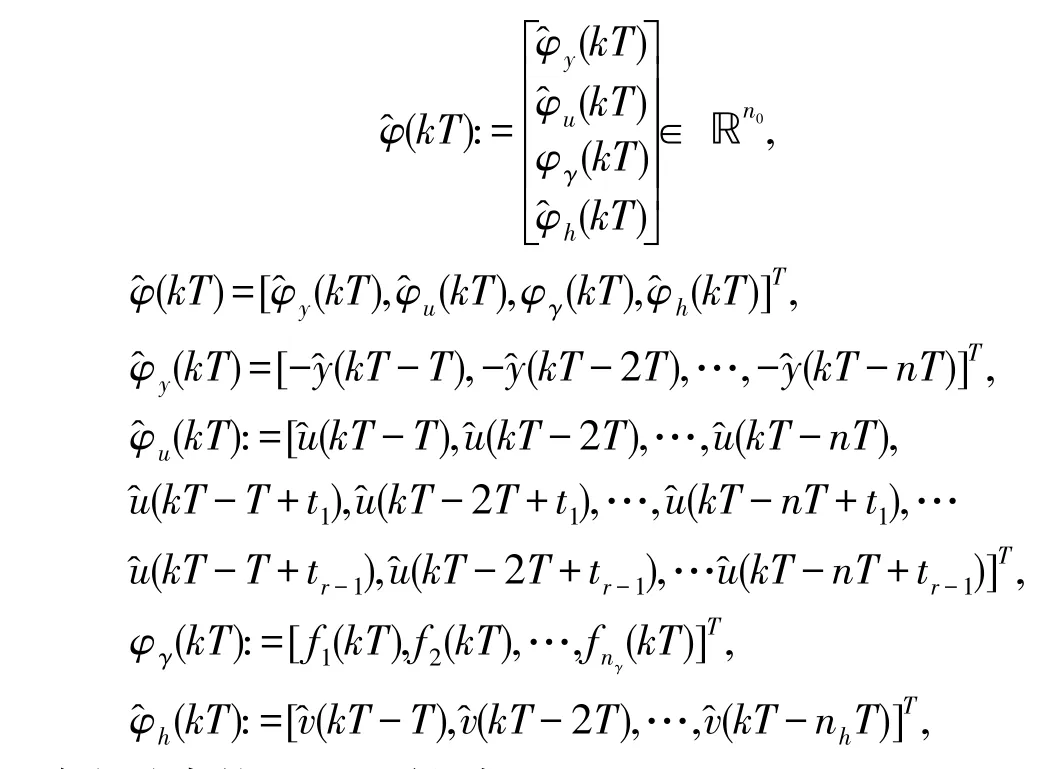
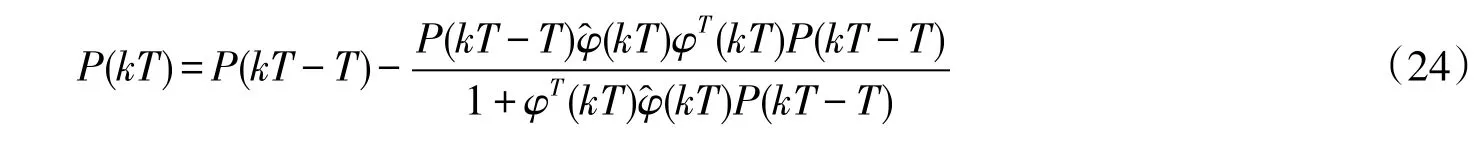
4　仿真实例

下面通过一个数值仿真实例验证算法的收敛性能.设系统的线性动态子模型Pc有如下的状态空间表达式：

令r=2，τ1=1s，τ2=2s，即t1=τ1=1s，t2=t1+τ2=3s，有色噪声模型为：ω（kT）=H（z）ν（kT），其中，H（z）=1+0.2z-1.用框架周期T离散化这个系统得到相应的输入输出表达式：

在仿真中，输入｛u（kT）｝和｛u（kT+t1）｝，取零均值单位方差的持续激励信号序列，｛v（kT）｝是零均值单位方差的白噪声.应用提出的算法估计未知参数，θ随迭代次数k变化的参数估计误差δ如图1所示.

图1　参数估计误差随迭代次数k的变化曲线

从图1可得到如下结论：算法的参数估计误差随k的增加而减小，证明了算法的有效性.同时该算法具有原理简单、计算精度高、且可以用于在线辨识等特点.但是，由于多采样率非线性系统待辨识参数多，协方差矩阵P是一个维数较大的矩阵，增加了算法的计算负担.研究提出计算量小、精度高的多采样率非线性系统辨识算法将是下一步的研究方向.

［1］丁锋.系统辨识新论［M］.北京：科学出版社，2013：1-10.

［2］丁锋.系统辨识：辨识方法性能分析［M］.北京：科学出版社，2014:110-135.

［3］LIU Y，BAI EW.Iterative identification of Hammersteinsystems［J］.Automatica，2007，43（2）:346-354.

［4］ÅSTRÖM KJ，EYKHOFF P.System identification-asurvey［J］.Automatica，1971，7（2）:123-162.

［5］VÖRÖS J.Parameter identification of discontinuous Hammersteinsystems［J］.Automatica，1997，33（6）:1141-1146.

［6］VÖRÖS J.Recursive identification of Hammersteinsystems with discontinuous nonlinearities containing dead-zones［J］.IEEE Transactions on Automatic Control，2003，48（12）:2203-2206.

［7］VÖRÖS J.Iterative algorithm for parameter identification of Hammersteinsystems with twosegment nonlinearities［J］.IEEE Transactions on Automatic Control，1999，44（11）:2145-2149.

［8］VÖRÖS J.Modeling and parameter identification ofsystems with multisegment piecewiselinear characteristics［J］.IEEE Transactions on Automatic Control，2002，47（1）:184-188.

［9］DING F，SHI Y，CHEN T.Auxiliary model-based least-squares identification methods for Hammerstein output-errorsystems［J］.systems and Control Letters，2007，56（5）:373-380.

［10］DING F，LIU XP，LIU G.Identification methods for Hammerstein nonlinearsystems［J］.Digitalsignal Processing，2011，21（2）: 215-238.

［11］VANBEYLEN L，PINTELON R，SCHOUKENS J.Blind maximum likelihood identification of Hammersteinsystems［J］.Automatica，2008，44（12）:3139-3146.

［12］WANG DQ，CHU Y，et al.Auxiliary model based RELS and MIELS algorithm for Hammerstein OEMAsystems［J］.Computers and Mathematics with Applications，2010，59（9）:3092-3098.

［13］WANG DQ，CHU Y，et al.Auxiliary model based recursive generalized leastsquares parameter estimation for Hammerstein OEARsystems［J］.Mathematical and Computer Modelling，2010，52（1）:309-317.

［14］BAI EW.Frequency domain identification of Hammerstein models，Block-oriented Nonlinearsystem Identification［M］.London:springer，2010:161-180.

［15］GOETHALS I，Pelckmans K，et al.Subspace identification of Hammersteinsystems using leastsquaressupport vector machines［J］.IEEE Transactions on Automatic Control，2005，50（10）:1509-1519.

［16］李秀英，韩志刚.非线性系统辨识方法的新进展［J］.自动化技术与应用，2005，23（10）：5-7.

［17］王峰，邢科义，徐小平.辨识Hammerstein模型方法研究［J］.系统仿真学报，2011，23（6）：1090-1092.

［18］YAMAMOTO Y，Khargonekar PP.Frequency response ofsampled-datasystems［J］.IEEE Transactions on Automatic Control，1996，41（2）:166-176.

［19］LU WP，FISHER G.Output estimation with multi-ratesampling［J］.International Journal of Control，1988，48（1）:149-160.

［20］DING J，LIN JX.Modifiedsubspace identification for periodically non-uniformlysampledsystems by using the lifting technique［J］.Circuitssystems andsignal Processing，2014，33（5）:1439-1449.

［21］LIU YJ，DING F，Shi Y.Leastsquares estimation for a class of non-uniformlysampledsystems based on the hierarchical identification principle［J］.Circuitssystems andsignal Processing，2012，31（6）:1985-2000.

Identification Algorithm Research on the Multiratesampling Nonlinearsystem with Moving Average Colored Noise

LI Xiangli，XIA Jing，CHEN Wei（School of Electric and Automatic Engineering，Changshu Institute of Technology，Changshu 215500，China）

Based on the auxiliary model method，the leastsquare recursive algorithm is derived for the nonlinear output error moving averagesystem.Insummary，this paperstudies and derives the identification algorithms for nonlinearsystem with multiratesampling，and the effectiveness of the algorithms is illustrated by Matlabsimulations.

nonlinearsystem；multiratesampling；auxiliary model；moving averagesystem

TP274

A

1008-2794（2015）04-0058-06

2016-05-30

江苏省高校自然科学基金“生物发酵过程的非线性软测量建模及优化”（15KJB120001）；常熟理工学院校级科研项目“精馏过程中多采样率非线性系统建模及目标优化方法研究”（XZ1504）

李向丽，讲师，工学博士，研究方向：非线性建模、参数辨识，E-mail：Lixiangli@cslg.cn.