多楔带振动图像测量数据插值分析算法研究

廖义德，何超，汪恩军，肖俊，雷进宇

（1.武汉工程大学机电工程学院，湖北武汉430205；2.武汉工程大学交通研究中心，湖北武汉430074；3.武汉理工大学智能交通系统研究中心，湖北武汉430063）

多楔带振动图像测量数据插值分析算法研究

廖义德1，何超1，汪恩军2，肖俊1，雷进宇3

（1.武汉工程大学机电工程学院，湖北武汉430205；2.武汉工程大学交通研究中心，湖北武汉430074；3.武汉理工大学智能交通系统研究中心，湖北武汉430063）

利用高速相机对带轮间多楔带振动数据进行测量.在图像处理的基础上，为了全面获取多楔带的振动信息，弥补多楔带高速运转过程中相机获取数据的不足，将带-轮驱动系统的多楔带简化为横向振动弦线，采用等距抽样定理提取弦线节点数据并运用5种不同的一维插值函数进行计算分析，将分析结果与高速相机实测到的全部振动数据进行比对，然后对实测值与插值进行误差分析.结果验证了3次Hermite插值的实用性和有效性，为多楔带振动特性的分析提供了理论依据.

图像处理；多楔带；插值分析；振动特性

多楔带振动是引起汽车发动机前端附件驱动系统噪声、磨损、带打滑的主要原因之一，研究多楔带的振动对于前端附件驱动系统的优化具有重要意义.在多楔带振动分析中，不同的算法对多楔带振动信息的获取有不同的影响.早期对多楔带振动特性的研究，主要是将带简化为运动弦线或纵向运动梁的模型，然后运用数学函数及方程等进行理论计算分析，但多楔带实际的运动形态与理论计算尚有偏差.Ulsoy等［1］将多楔带看作运动的弦线，分析了带中张紧力的变化而导致振动的不稳定性，使带产生较大的横向振动，Kong和Parker［2-4］将多楔带看作纵向运动梁，建立了三轮一带系统振动模型，该方法只研究了稳定状态下的横向位移及系统固有频率的变化规律.上官文斌等［5］将单根多楔带相邻两轮之间的带段简化成纵向运动梁，推导了纵向运动带（梁）横向振动固有频率的计算方程.以往的研究中，很少有学者对多楔带真实振动信息进行计算分析，由于多楔带的振动激烈而无规则，受多种外部因素的干扰，以上研究得到的数据不能完全反映实际的振动信息.图像处理是获取多楔带振动数据的一个重要途径，具备全面获取多楔带振动信息的能力.测量的数据经过处理后可以真实的还原多楔带的振动过程，但实际工况中由于多楔带运转速度快，普通的高速相机存在帧率不足、采集图片少等情况，未获取到的数据会造成振动信息的缺失.插值分析通过离散的输入采样点建立相关函数求出任意位置的函数值［6］可以获取较多的数据，对运动形态的恢复有着重要的弥补作用.插值函数适合于模拟随时间变化激烈振荡的物理过程，如车桥耦合插值分析［7］.在工业计算、机械研究方面有着非常重要的作用.因此采用插值分析可以全面的反映多楔带振动形态的变化过程.

本文采用非接触式高速摄像机获取多楔带动态图像信息，通过MATLAB图像处理提取图像中多楔带标志点的平面坐标信息.基于附件轮-带耦合振动模型，将实测坐标数据按等间距分成两组，防止了抽样的周期性偏差.对提取出的等距抽样数据进行插值分析，运用5种一维插值函数进行计算，将不同的插值算法得到的数据与高速相机实测的真实数据进行了误差匹配分析，比对计算结果验证了各种方法的误差大小.

1　多楔带动态数据信息采集与预处理

1.1采集系统平台搭建

发动机多楔带动态特性信息采集系统是由帧速为240帧/秒的工业摄像机、发动机试验台、光电编码器、激光测距仪、驱动电机、变频器及台架等构成.驱动电机和变频器使该系统提供稳定的转动，编码器获取驱动轮准确的转速.高速摄像机置于发动机多楔带正前端，采集多楔带标志点的振动图像.图1为实验平台示意图，由于视角原因部分设备未能在示意图上显示.

图1　多楔带实验平台

1.2多楔带标志点图像处理

为了准确获取多楔带的振动特性，先对发动机前端多楔带进行人工标记，高速摄像机获取连续多帧图像，通过特征提取、边缘检测等对多楔带图像中的人工标志点进行跟踪识别.在数据获取过程中，由于运动、光照等因素的干扰，对图像质量存在一定的影响，需要经过数据滤波、灰度图二值化、特征增强、边缘检测等［8］才能获取标志点单个像素的准确坐标.处理流程图如图2所示：

图2　多楔带标志点处理过程

对一帧图像经过一系列图像处理的算法后准确的获取了人工标志点的像素坐标，标志点位置图像如图3所示，然后对摄像机采集到的连续多帧图像进行同一标志点的跟踪识别，获得该标志点的坐标连续变动位置，像素单位作为计算量度应用在下面振动参数的计算中.

图3　边缘检测提取单个像素中心点

1.3多楔带数据旋转调整

在弦线耦合振动的基础上，将多楔带看作运动弦线，振动特性从高速摄像机采集的多帧图像中获取，先对柔性带某一处进行标示，在系列图片中跟踪同一标示点，绘制出标示点运动轨迹，直观描述出柔性带完整的波动形状.部分实测标志点的二维坐标如表1所示.表1中采集到标志点的中心坐标时间单位是秒，横坐标以及纵坐标数据大小是以像素为单位，根据摄像机的相关数据，计算得到一个像素边长大小约为0.233 mm.

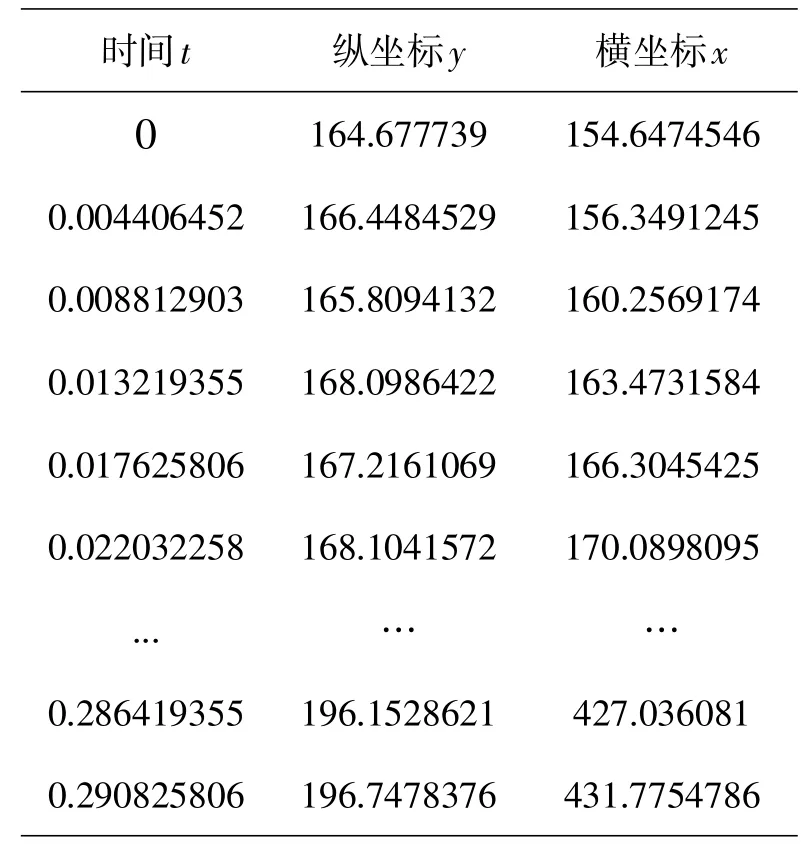
表1　连续多帧图像标志点中心坐标

以相邻驱动轮及从动轮间的带段作为研究对象，假定带的抗弯刚度较小，将带简化为纵向运动的黏弹性弦，理论振动模型如图4所示，其中，多楔带沿X方向作纵向运动，沿W方向作横向振动.在发动机实验台轮系中，以静止时柔性带和两带轮的切点为基准点，建立直角坐标轴.即在表1中起点和终点作为两切点坐标，部分振动数据的实际二维坐标相对变化如图5所示.

图4　多楔带理论振动模型

图5　标志点二维坐标

实测到的坐标在大的范围内所呈现的微小变动分析较难，要准确的获得柔性带微小的振动，必须将静止时的带轮弦线调整到水平状态，实测到的所有的标志点的坐标也随之相对旋转同一个角度，多帧图像中的标志点经过二维旋转后如图6所示，标志点和基准轴一起旋转，相对于基准轴的位移并没有发生改变.旋转之后的振动波形图能够清楚的反应柔性带的微小变化，清晰的反映出多楔带的振动特性.本文引入计算机图形学［9］的二维旋转变换算法：二维旋转是指坐标系不动，物体或点绕坐标轴旋转一个角度β，具体方法为：

假设向量a=（xa，ya），把它旋转β角之后，得到向量b=（xb，yb），如果向量a与x轴的夹角为α，向量a的长度，则xa=rcosa，ya=rsinα，向量b由向量a旋转而来，

将旋转方法应用于实测的连续多帧标记点的坐标，图5原始标志点的二维坐标即变成如图6.

由图6可以看出，经过旋转调整后的标志点的变化特性变得更加准确清晰.振动时的标志点变化相对于静止带轮弦线的区分度更大，数据清晰可见.

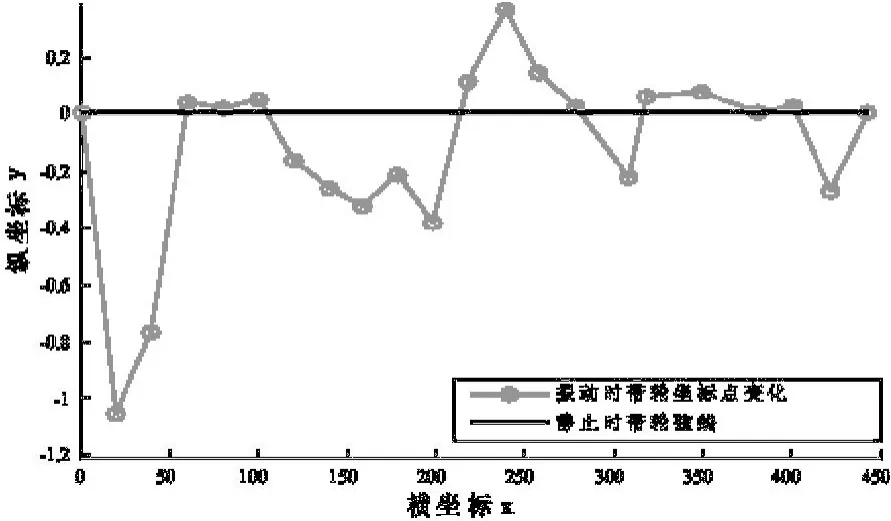
图6　经过二维旋转变换后的坐标

2　多楔带振动数据插值分析

2.1实测数据进行等距抽样

如图7所示，由240帧/秒的工业相机实测到的较低速度时多楔带数据变化曲线，多楔带简化成弦线模型，通过棋盘标定法将像素单位换算成毫米单位：

多楔带两带轮间振动过程由104帧静止图像构成，提取每一帧图像的多楔带标志点经过一系列图像处理，完成标志点的跟踪识别，真实的还原了多楔带的运动过程.

图7　实测到的带段间全部数据

现对多楔带振动弦线数据进行等距抽样，建立数学模型.为了避免周期性偏差带来的影响，依次序提取52组数据的第一、二个点，得到的弦线模型如图8所示.

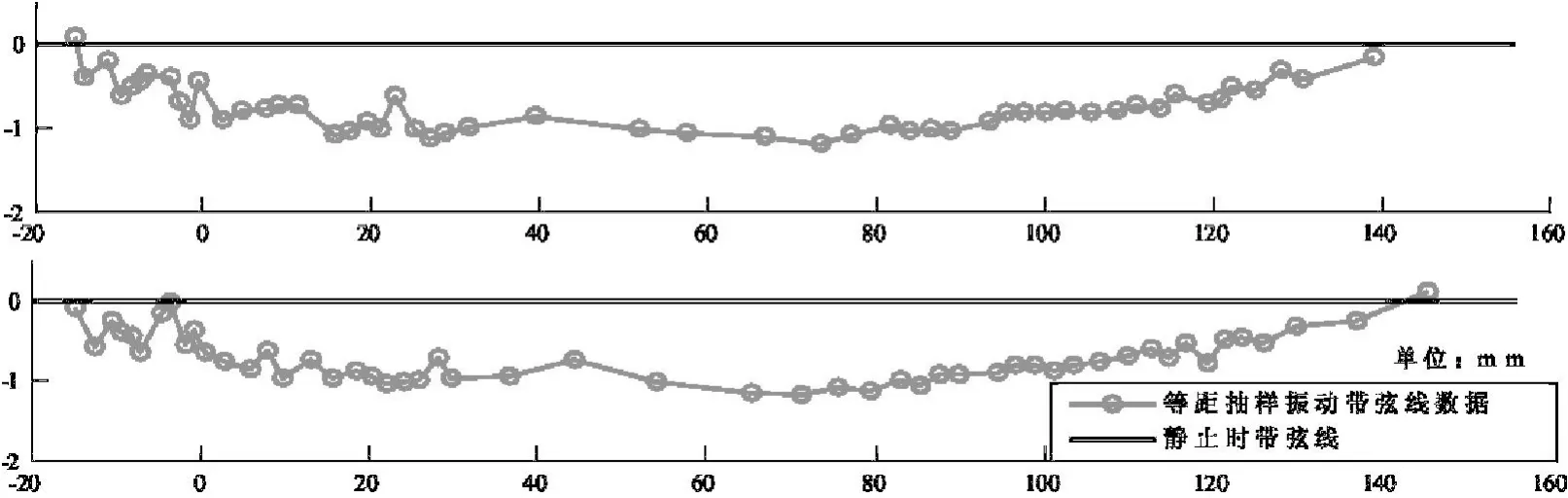
图8　起点分别为一、二等距抽样点

2.2一维插值分析

插值是在已知数据之间寻找估计值的过程.在信号处理和图像处理中，插值是极其常用的方法，本文运用最邻近、线性、3次样条、分段3次Hermite，以及快速傅立叶5种一维插值方法［10］分别计算，分析插值结果与实测点之间的偏差大小，一维插值多项式运用函数yi=interp1（x，y，xi，method），快速傅立叶运用函数y=interpft（x，n，dim）来计算分析.在已知抽样数据的最邻近点设置插值点，对插值点的数据四舍五入.对超出范围的点将返回一个NaN（Not a Number），这些插值函数在获得数据的平滑度、时间复杂度上面有不同的性能，最终得出最佳的一维插值方法，经过5种一维插值的等距抽样点与实测到的坐标点如图9所示.

图9　5种一维插值算法分析图

由图9可知最邻近插值方法是最快的插值方法，但是数据平滑方面最差，得到的数据是不连续的.线性插值执行速度较快，但其数据平滑方面优于临近插值，有一定的精度，且数据变化是连续的，3次样条插值函数具有局域性，处理速度最慢，但可以产生最光滑的结果，偏差也较小，处理效果相对较好，已经成为一种广泛的插值方法.分段3次厄米多项式插值处理速度不及线性插值，但得到的数据和一阶导数都是连续的.一维快速傅立叶插值通过傅立叶变换把输入数据变换到频域，然后用更多点的傅立叶逆变换变换回时域，其结果是对数据进行增采样.

3　插值数据误差分析

由于摄像机微小的误差以及带轮振动的不确定性，振动特性相对于静止时的带轮弦线连续性并不明显，并且标志点不同坐标之间形成多段弯曲，呈现无规则的变化，各个节点处不光滑.多种插值算法在原采样点上精确还原原函数值仅在理论上可能，相对于实测点都存在一定误差.鉴于这种情况，在已有的若干准确测量基础上，对各个插值点与实测点进行误差分析计算，将分析结果与高速相机实测到的全部振动数据进行比对，得出每一种插值方法的平均方差.具体方法为：对已经实测到的n个横坐标点x1，x2，…xn，以及对应的函数值y1，y2，…yn，经过等距抽样后，得到间隔为2个点的抽样坐标点，经插值函数计算得到跟实测点数目相同的点，对插值区间内的所有点进行误差匹配运算，均方差通过下式求得：

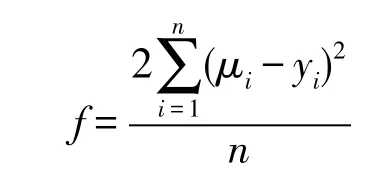
偏差的最大最小值由（μi-yi）来计算，计算过程由MATLAB实现.计算出最大最小偏差和平均方差列在表2、表3中.

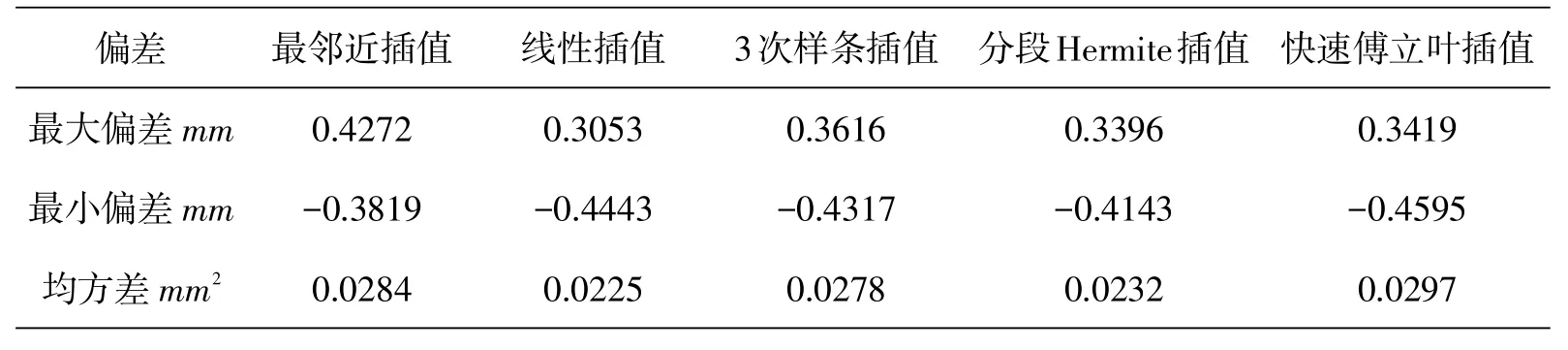
表2　5种插值数据偏差及方差信息（等距抽样1）

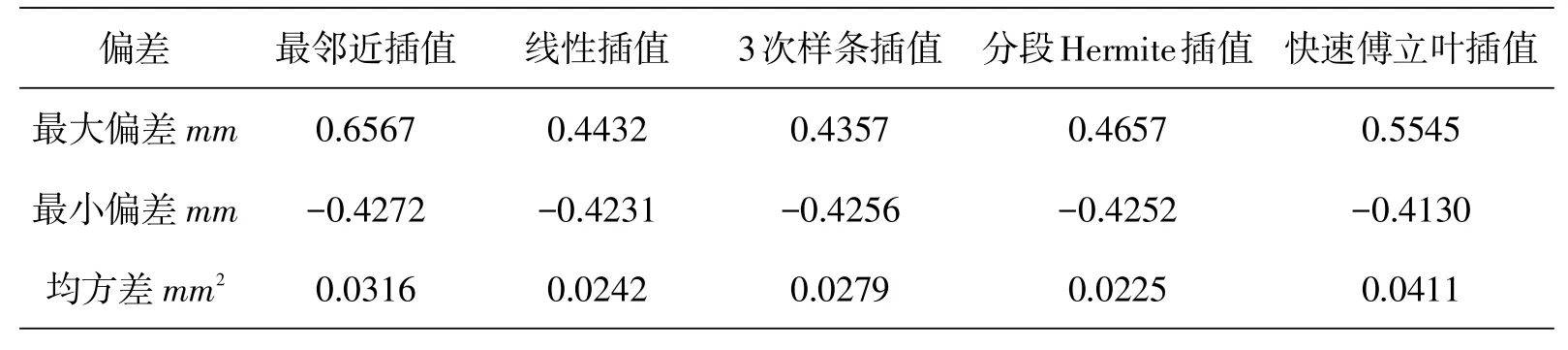
表3　5种插值数据偏差及方差信息（等距抽样2）

从表2可以看出5种插值函数的最大偏差相隔不大，其中最小的是线性插值，最大的是最邻近插值，在最小偏差中比较各个数值的绝对值，可以得到线性插值最小.但在均方差中，线性插值与分段Hermite插值最小；从表3中可以看出类似于表2的情况，即各个插值函数中，线性插值、3次样条插值和分段Hermite插值相对较小，最小偏差的绝对值也是这3种相对较小，但是在均方差中，和表2情况一样，都是线性插值与分段Hermite插值最小.

综合表2和表3，可以看到总体上线性插值与分段Hermite插值的最大偏差与最小偏差比较接近，但是由于整体的平均方差才是最能体现出插值点与实测点之间的离散程度，因此实验结果表明，分段Hermite插值函数总体平均方差最小，与真实的实测点离散程度最小，重构多楔带振动的坐标误差最小.对多楔带弦线数据的插值显示，最接近实测点的是分段Hermite插值法，当多楔带转动速度的增大时，摄像机获取多楔带振动的数据将会减少，通过该插值算法重构弦线的振动数据可以弥补相机的不足，分段3次Hermite插值的实用性和有效性为多楔带的研究提供了技术支持.

4　结语

（1）设计了一种多楔带轮系特性采集系统，非接触式高速摄像机通过人工标志点获取了发动机多楔带动态特性信息，减小了传统接触式采集系统带来的误差，提高了实验的准确性.给出了标志点中心单个像素的坐标的处理方法，重构了两带轮多楔带之间的运动过程.

（2）分段Hermite插值法具有误差小，总体离散平稳的优点，弥补了转速提高的情况下相机部分帧缺失的问题，较真实的还原了多楔带段间振动相互关联过程.本文的计算方法和结论，为多楔带振动特性的计算分析和优化提供了理论依据.

［1］HWANGs J，PERKINS N C，ULSOY A G.Rotational response andslip prediction ofserpentine belt drivesystems［J］.Journal of Vibration and Acoustics，1994，116：71-78.

［2］KONG L Y，PARKER R G.Equilibrium and belt-pulley vibration coupling inserpentine belt drives［J］.Journal of Applied Mechanics，2003，70：739-750.

［3］KONG L Y，PARKER R G.Coupled belt-pulley vibration inserpentine drives with belt bendingstiffness［J］.Journal of Applied Mechanics，2004，71：109-119.

［4］PARKER R C.Efficient Eigensolution，Dynamic Response，and Eigen-sensitivity ofserpentine Belt Drives［J］.Journal ofsound and Vibration，2004，270（1-2）：15-38.

［5］上官文斌，杨嘉威，冯骁.单根多楔带附件驱动系统中各带段横向振动固有频率计算方法的研究［J］.工程力学，2014，31（12）：193-199.

［6］吴春发，李星.地质模拟中数据插值方法的应用［J］.地球信息科学，2004，6（2）：50-52

［7］余华，吴定俊.Hermite插值在车桥耦合振动中的应用［J］.振动与冲击，2006，25（2）：38-40.

［8］秦襄培，郑贤中.MATLAB图像处理宝典［M］.北京：电子工业出版社，2011：204-345.

［9］高春晓，赵清杰，张文耀.计算机图形学［M］.2版.北京：人民邮电出版社，2007：126-130.

［10］STOER J，BULIRSCH R.数值分析引论［M］.南京：南京大学出版社，1995：42-140.

A Research on Interpolation Analysis Algorithm inserpentine Belt Measured Data of Vibration Image

LIAO Yide1，HE Chao1，WANG Enjun2，XIAO Jun1，LEI Jinyu3
（1.School of Mechanical and Electrical Engineering，Wuhan Institute of Technology，Wuhan 430205；2.Transportation Research Center，Wuhan Institute of Technology，Wuhan 430074；3.Intelligent Transportsystem Research Center，Wuhan University of Technology，Wuhan 430063，China）

Theserpentine belt vibration data of pulleys are measured with high-speed video camera on the basis of image processing.In order to acquire comprehensive vibration information aboutserpentine belt and compensate deficiency of video data collection in the process of highspeed vibration，the belt of band-wheel drivesystem issimplified as a lateral movingstring.Additionally，extractedstring node data with equidistantsampling theorem and 5 different one-dimensional interpolation functions are applied in analysis.Finally，the error of measured value and interpolation is calculated by comparing the measured vibration data of the high-speed camera.The results validate the practicality and effectiveness of Cubic Hermite Interpolation，which can provide a theoretical basis for the analysis of the vibration characteristics of theserpentine belt.

image processing；serpentine belt；interpolation analysis；vibration characteristics

TH132；TK423

A

1008-2794（2015）04-0028-10

2015-03-10

湖北省自然科学基金“基于高频时序图像分析的汽车发动机轮系动态特性检测研究”（2014CFB7777）；国家自然科学基金“桥区水域船舶行为识别与可视化应用研究”（51479155）

雷进宇，博士，研究方向：数据可视化与可视分析，E-mail：jylei@whut.edu.cn.