瞬态空燃比的自适应模糊滑模补偿控制＊

王立标，李岳林

（1.台州学院　机械工程学院，浙江　台州　318000；2.长沙理工大学　汽车与机械工程学院，湖南　长沙　410076）

瞬态空燃比的自适应模糊滑模补偿控制＊

王立标1，李岳林2

（1.台州学院机械工程学院，浙江台州318000；2.长沙理工大学汽车与机械工程学院，湖南长沙410076）

发动机是一种强耦合的非线性、时变性系统，很难建立精确的数学模型。为了提高发动机瞬态工况的空燃比控制精度，基于Lyapunov法设计了一种自适应模糊滑模瞬态空燃比补偿控制系统。该控制系统采用自适应模糊理论逼近被控对象，而无需依赖被控对象的数学模型。通过无补偿、PID和自适应模糊滑模瞬态空燃比三种控制策略的仿真比较试验可得，采用自适应模糊滑模补偿控制策略能使空燃比在节气门突变时有效跟踪目标值，使其稳态误差小于±0.8，且滑模函数能快速收敛于零点。该控制系统具有较强的自适应性和鲁棒性。

瞬态空燃比；滑模控制；自适应控制；模糊

0　引言

当发动机空燃比偏离当量值1%，汽车尾气中的CO、HC和NOx化合物急剧增加。为了降低汽车尾气的排放和提高燃油利用率，通过空燃比的精确控制来提高三元催化器的转化效率已成为研究的热点［1］。

由于发动机是一种多变量的高度非线性系统，传统的空燃比控制方法很难得到精确控制［2~4］。近年来，许多新的控制方法被应用于精确空燃比控制中。Choi提出了基于喷油脉宽观测器的滑模控制方法，降低了空燃比的脉动，但未考虑动态油膜存在的影响［5］。文献［6，7］基于神经网络离线或在线的数据训练进行空燃比模型预测控制，仿真结果表明，空燃比能保持在当量值附近，但需要大量的网络训练数据或依赖于被控对象的数学模型，难以适应实时控制应用。

随着模糊理论的发展，自适应模糊控制理论已被广泛应用于非线性控制领域［8~10］。本文提出了一种自适应模糊滑模瞬态空燃比补偿控制器，由于模糊具有万能逼近的特性，该方法无需依赖于被控对象的数学模型，并且滑模控制具有较强的抗干扰能力，因此当发动机处于瞬态工况时，能使空燃比精确地维持在当量值附近。

1　动态油膜x-τ模型

燃油喷射器喷射的燃油一部分随空气直接进入气缸燃烧，另一部分在进气歧管壁面上形成油膜且油膜又以一定的速率逐渐蒸发进入气缸，产生了油膜效应。C.F.Aquino教授提出的动态油膜x-τ模型如图1所示。其动态方程［11］：

其中，根据文献［12］，xf和τf分别表示为：

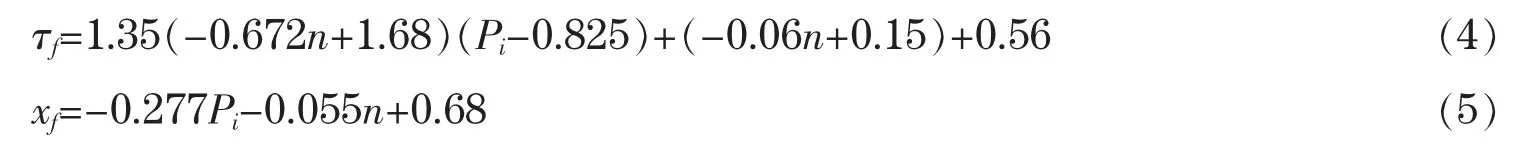
式中，Pi为进气歧管压力；n为发动机输出转速。

当发动机工作于稳态工况时，由于油膜处于平衡状态，可以忽略油膜的动态效应，进入气缸的燃油量与喷油器喷射的燃油量相等。当发动机运行在瞬态工况下，由于油膜的动态效应使得进入气缸的燃油量不等于实际喷射量，导致空燃比偏离理论值。为了使空燃比能继续保持在理论值附近，需采取油膜补偿控制，根据式（6），推导出瞬态工况下加入补偿控制后的喷油流量为：

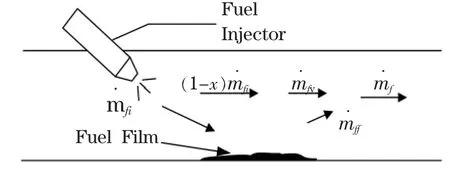
图1　动态油膜x-τ模型

2　瞬态空燃比控制系统设计

2.1控制系统结构

自适应模糊滑模空燃比补偿控制系统如图2所示。发动机总喷油量由基本喷油量和补偿喷油量组成，基本喷油量直接由发动机进气量获得，补偿喷油量由自适应模糊滑模控制器输出。自适应模糊系统通过输入空燃比目标值和实际值，根据模糊自适应律，不断更新模糊系统输出。模糊系统输出为逼近发动机模型中的不确定模型，并输入到滑模控制器，从而实现无需依赖控制对象参数的自适应模糊滑模空燃比控制系统，该控制系统具有很强的自适应能力。

图2　自适应模糊滑模空燃比控制结构

2.2滑模控制器设计

其中：x=［x1，x2］T；n为发动机转速；Pi为进气歧管压力；T为发动机水温；v为噪声干扰；u为补偿喷油流量；d为负载转矩且，D为正常数。

令目标空燃比λd=xd，则空燃比误差及其变化率为：

设计滑模函数为：

则对滑模函数求导可得

其中f=f（x，n，pi，T，v）.

定义Lyapunov函数：

并对其求导

假设f已知，设计控制律为

将式（13）代入（12），得

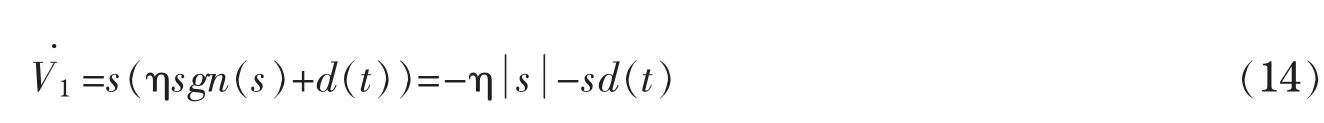
为了实现无需控制对象模型的自适应模糊滑模控制系统，利用模糊万能逼近特性，以来逼近f函数。

2.3自适应模糊

发动机是一种强耦合的非线性、时变系统，数学模型很难精确建立。基于模糊理论，逼近式（13）中的f函数。模糊系统的输入为x=［x1，x2］T.由于模糊输入只考虑变量xi，则f函数可表示为f（x），对每个输入分别设计5个模糊集，则共有25条模糊规则。

（1）对输入变量xi，i=1，2。采用高斯型隶属函数，设计模糊集，其中i=1，2，li=1，2，3，4，5。

（2）设计25条模糊规则，第1条和第25条规则如下［13］：

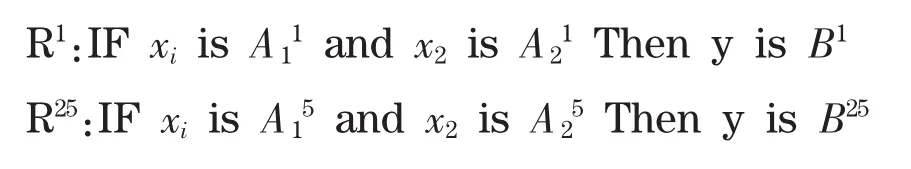
则，第j条模糊规则为

其中，y为每条模糊规则输出，j=1，2，…，25，Bl1l2为模糊规则的结论集。

（3）采用乘积推理、单值模糊器和中心平均反模糊求解器，得到模糊系统的最终输出为

引入模糊基向量ξ（xi），式（15）改写为

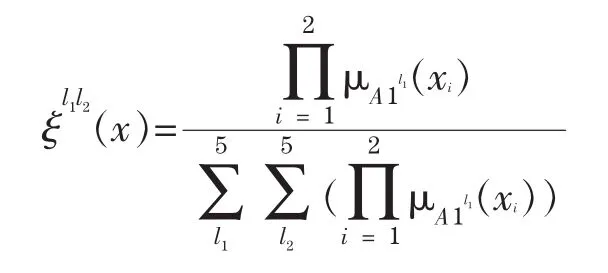
2.4控制系统稳定性分析

设最优逼近常数θ*，对于任意小的正常数ε，则

根据式（16）和（17）可得出模糊系统的逼近误差为

设计自适应模糊滑模控制律

则

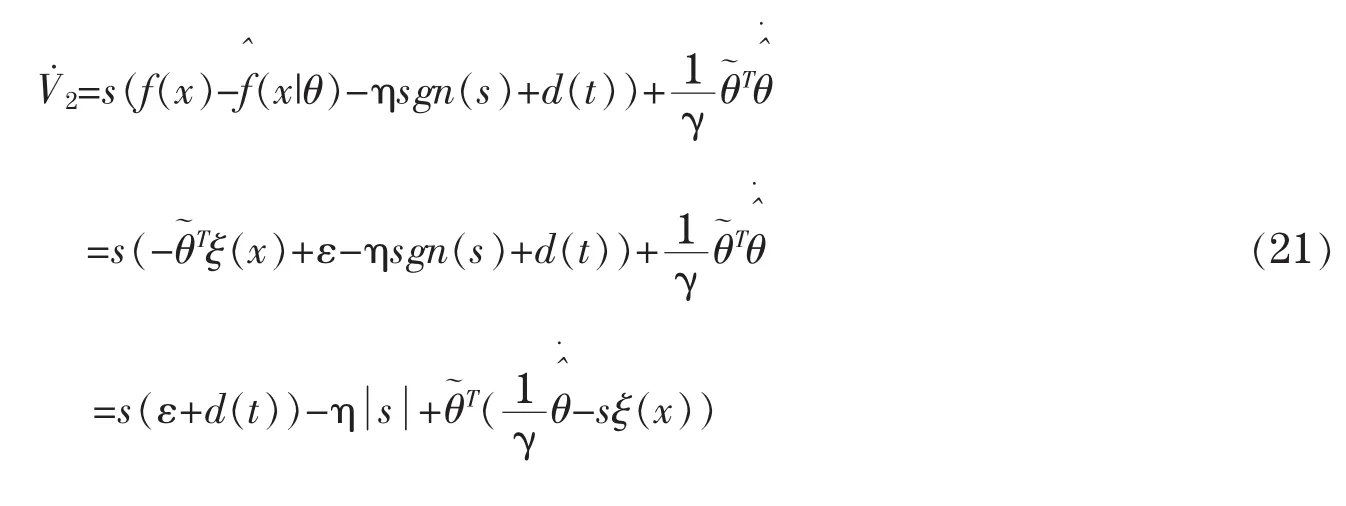
取模糊自适应律为

将自适应律代入式（20）得

3　仿真试验

为了验证控制系统的有效性，首先根据文献［4］在Matlab/Simulink下搭建了汽油机平均值模型，其次对无补偿、PID和自适应模糊滑模三种空燃比控制系统进行了对比仿真试验。对的试验中，如图3模糊系统取5种隶属度函数对输入xi进行模糊化。自适应模糊滑模控制器中，自适应律初始值取0.1，γ=0.5， η=0.5。PID控制参数采用信号约束法进行在线整定［15］，可得kp=5，ki=0.02，kd=0.05。

仿真过程中，节气门从33°突变到39.5°，如图4所示。仿真结果如图5-8，图5为基于PID和自适应模糊滑模补偿控制的补偿喷油量。图6分别为三种控制系统的总喷油量。图7为三种控制系统的空燃比变化情况，无补偿空燃比控制系统在节气门突变情况下，空燃比明显偏离目标值，采用自适应模糊滑模控制系统空燃比稳态误差小于±0.8，而且比PID控制系统在突变节气门下，能快速跟踪目标空燃比，具有较强的鲁棒性。图8为自适应模糊滑模控制器的滑模函数相轨迹，图中误差能收敛于零点，具有很强的自适应能力。

图3　模糊输入变量的隶属度函数　

图5　补偿喷油量　

图7　三种控制系统的空燃比　

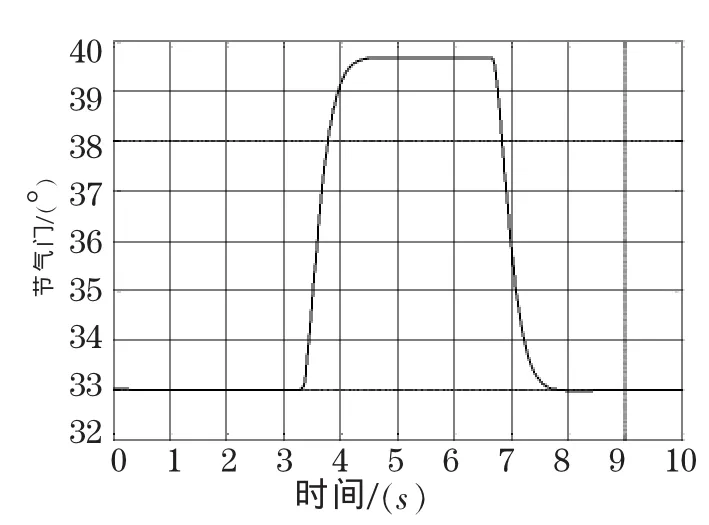
图4　节气门开度

图6　总喷油量

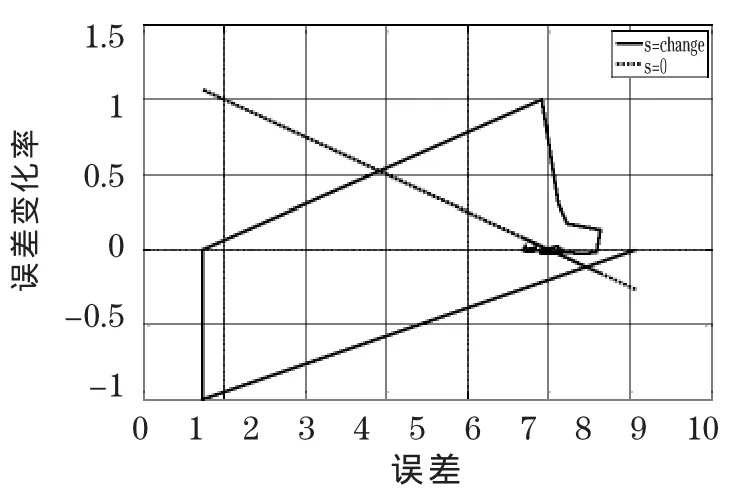
图8　滑模函数的相轨迹

4　结语

基于Lyapunov函数法设计了自适应模糊滑模瞬态空燃比补偿控制系统。该控制系统无需依赖于被控对象的具体数学模型，具有较强的鲁棒性。通过三种空燃比控制策略的对比仿真试验，采用自适应模糊滑模空燃比补偿器能使空燃比在节气门突变时能快速恢复到目标值，并使稳态误差小于±0.8，与无补偿控制相比，大大降低了瞬态空燃比的偏差。由于模糊理论可以采用查表法进行编程，因此该控制方法易于进一步进行发动机台架试验，具有一定的实际工程意义。

［1］Manzie C,Palaniswam i M,Watson H.Gaussian netw orks for fuel injection control［J］.Proceedings of the Institution of M echanical Engineers,Part D:Journal of Automobile Engineering,2001,215（10）:1053-1068.

［2］De Nicolao G,Scattolini R,Siviero C.Modelling the volumetric efficiency of IC engines:parametric,nonparametric and neural techniques［J］.Control Engineering Practice,1996,4（10）:1405-1415.

［3］TanY,Saif M.Neural-netw orks-basednonlinear dynam ic modeling for automotive engines［J］. Neurocom puting,2000,30（1）:129-142.

［4］Manzie C,Palanisw am i W,Watson H.Model predictive control of a fuel injection system w ith a radial basis function netw ork observer［C］//Neural Networks,2000.IJCNN 2000,Proceedings of the IEEE-INNS-ENNS International Joint Conference on.IEEE,2000（4）:359-364.

［5］Choi S B,Hedrick J K.An observer-based controller design method for improving air/fuel characteristics of spark ignition engines［J］.Control Systems Technology,IEEE Transactions on,1998,6（3）:325-334.

［6］Wang S W,Yu D L.Adaptive air-fuel ratio control with MLP network［J］.International Journal of Automation and Com puting,2005,2（2）:125-133.

［7］Sarasw ati S,Chand S.Online linearization-based neural predictive control of air fuel ratio in SI engines w ith PID feedback correction scheme［J］.Neural Computing and Applications,2010,19（6）:919-933.

［8］Lin T C,Chang S W,Hsu C H.Robust adaptive fuzzy sliding mode control for a class of uncertain discrete-time nonlinear system s［J］.International Journal of Innovative Com puting,Information and Control, 2012,8（1）:347-359.

［9］BlaiS,?krjanc I.A Robust Fuzzy Adaptive Control Algorithm for a Class of Nonlinear System s［M］.Springer Berlin Heidelberg,2013:297-306.

［10］Lin W.Adaptive Fuzzy Controller for Chaotic Systems w ith Mismatched Uncertainties and Unknow n Control Gain Matrix［J］.Journal of Computational Information Systems,2013,9（13）:5205-5212.

［11］Aquino C F.Transient A/F Control Characteristics of the 5 Liter Central Fuel Injection Engine［C］.SAE Paper:810494,1981.

［12］E.Hendricks.A generic mean value engine model for spark ignition engines［C］.The 41st Simulation Conference,SIMS 2000,DTU,Lyngby,Denmark.2000.

［13］王立新.模糊系统与模糊控制教程［M］.北京：清华大学出版社，2003:152-156.

Adaptive Fuzzy Sliding Mode Com pensation Control for Engine Transient Air Fuel Ratio＊

WANG Libiao1，LI Yuelin2
（1.School of Mechanical Engineering,Taizhou University,Taizhou 318000,China; 2.School of Automotive and Mechanical Engineering,Changsha University of Science and Technology,Changsha 410076,China）

It’s difficult to establish a precise mathematical model because the engine is a strong coupling nonlinear,time-varying system.Based on the Lyapunov method,a new method of adaptive fuzzy sliding mode com pensation(AFSMC)is adopted to im prove the engine transient air-fuel ratio control precision in this paper.The control object has been approximated by adaptive fuzzy system w ithout relying on the mathematical model.The simulation results show that the AFSMC controller not only can better track the target AFR com pared w ith the No Com pensation and PID controller as the throttle mutation,but also the steady-state error is less than±0.8 and the sliding function can quick ly converge,so that the AFSMC controller has strong adaptability and robustness.

transient air fuel ratio；sliding mode control；adaptive control；fuzzy

10.13853/j.cnki.issn.1672-3708.2016.03.006

（责任编辑：耿继祥）

2015-09-07

国家自然科学基金（51176014）。

王立标（1983-），男，浙江台州人，讲师，博士生，主要研究机电系统非线性动力分析及其控制。