高超声速飞行试验助推段弹道优化方法

张子明,蒋　劲,王西耀

(中国空气动力研究与发展中心 超高速空气动力研究所 高超声速冲压发动机技术重点实验室,四川 绵阳 621000)



高超声速飞行试验助推段弹道优化方法

张子明,蒋劲,王西耀

(中国空气动力研究与发展中心 超高速空气动力研究所 高超声速冲压发动机技术重点实验室,四川 绵阳 621000)

为减小高超声速飞行试验助推段飞行环境的恶劣程度,提出了一种生成三自由度最优弹道的方法。采用基于攻角编码的遗传算法,并用三次样条对攻角-时间历程进行平滑处理。优化过程首先搜索满足窗口参数的可行解,然后以攻角范围、最大动压、最大法向过载等参数为目标函数,以窗口参数为约束,搜索飞行环境恶劣程度最低的最优化弹道。计算结果表明,该算法能够避免理论弹道中存在局部高风险阶段的情况,并具有良好的鲁棒性。

高超声速飞行器;理论弹道;遗传算法;多目标优化

高超声速技术是当今世界各国竞相研究的热点。该技术由于涉及激波/边界层干扰、湍流转捩、非平衡流动等许多复杂的空气动力学关键问题,国内外仍在攻关之中,普遍采用地面试验、数值计算和飞行试验相结合的研究手段。

模型飞行试验[1-2]是针对单项或者多项空气动力学关键技术的飞行试验。由于试验模型在高马赫数下才能开始工作,因此,需要采用助推的方式,将其送入预定的试验窗口。在助推段,重力和负升力的综合作用使试验模型进入水平飞行的试验窗口。本文研究的飞行试验模型采用类似于图1所示的升力体外形[3]。与其他飞行试验相比,高超声速试验模型的飞行试验具有以下特点:①升力体外形的试验模型压心靠前、质心靠后,导致舵面配平性能较差,只能在小攻角条件下飞行;②试验模型的尖锐前缘对热环境提出了更高的要求,需要尽量降低助推段的飞行动压;③受试验模型质量及结构的约束,飞行过程中的法向过载不宜太大;④跨声速段为高风险飞行阶段,应避免大攻角飞行;⑤试验窗口的弹道参数通常较为苛刻,允许的偏差较小。

图1　飞行试验模型示意图

基于上述特点,高超声速试验模型的助推段弹道设计应考虑以下4个关键因素:①攻角变化范围。针对升力体构型的试验模型,大的负攻角状态下纵向气动特性可能是静不稳定的,当与某些侧滑角组合时,航向也是静不稳定的。另外,强烈的纵横耦合力矩和上、下气动舵面效率差异显著的问题,也将给横航向控制带来难度。因此,弹道设计应避免采用大的负攻角。②跨声速段攻角限制。试验模型的空气动力非线性特征突出,跨声速段气动力和力矩特性变化剧烈,为高风险飞行阶段,应当避免采用大的弹道机动。例如,美国飞马座空射运载火箭以Ma=0.8投放后,以零攻角加速(同时自然降高)到约385 m/s(Ma=1.3)后才开始以大攻角向上拉升。③舵偏角变化范围。模型的升降舵效率相对较低,导致升降舵偏角较大,且在拉偏情况下,由于舵偏角与舵偏效率的非线性变化规律容易导致舵偏饱和的情况,因此,需要尽量降低理论弹道的配平舵偏角。④进入窗口前的姿态调整。考虑到助推器的拖尾段不利于对攻角的精确控制和稳定,且助推器工作时间存在一定的不确定量,因此,弹道设计时,在进入窗口前需要尽量减小攻角变化率,并提前将攻角调整到零攻角附近。

由此可见,高超声速飞行试验的助推段弹道优化,需要针对由特定的助推装置、气动性能、操稳特性、质量特性及结构约束等环节构成的飞行系统,寻找与该系统最匹配的飞行弹道,让试验模型以最“舒服”的方式飞行到试验窗口,并尽量降低飞行环境的恶劣程度,确保试验成功。这一优化目标与常规的能量最小或时间最短等优化目标存在显著的区别。

目前,关于优化计算的方法和理论已经较为全面[3],这些最优化理论提供了多种优化的方法。常用的优化方法有动态规划、二次规划法、遗传算法等方法。

动态规划是美国数学家Bellman R等人于1951年提出的解决多阶段决策过程的最优化方法。该方法在工程技术、经济、工业生产及军事等部门都有广泛的应用。但是,动态规划方法也存在两大弱点[4-6]:一是利用最优原理得到函数方程后,没有一种统一的处理方法,需要根据具体问题结合数学技巧来求解;二是所谓的“维数障碍”,即当变量个数太大时,受计算机限制而无法求解。例如,Harada A,Miyazawa Y等人采用动态规划法对民航客机的纵向轨道进行了优化[7-8]。尽管这些研究工作已经极力考虑了“维数障碍”的问题,但当变量数达到20以上时,计算依然显得困难。

二次规划已经成为运筹学、经济数学、系统分析和组合优化科学的基本方法。在航空航天领域,Ran D采用序列二次规划算法,研究了最小时间拦截问题[9],郑总准等人采用序列二次规划算法,对再入轨道进行了优化[10],其最优化目标为总加热量最小。刘欣等人采用序列二次规划法对助推导弹进行了弹道优化[11],傅瑜等人也采用序列二次规划法,对可重复使用助推器飞行器的轨迹进行了优化研究[12]。

遗传算法(GA)是Holland J于1975年提出的一种智能的全局优化算法[13]。近年来,采用遗传算法进行弹道优化的研究也不少。例如,齐照辉等人采用遗传算法对弹道导弹助推段轨道进行了优化[14],杨遵等人采用遗传算子粒子群优化算法进行任务优化分配,对无人机的航路进行了规划[15]。

所有上述的弹道优化工作,都是值得肯定和借鉴的。但是,高超声速飞行试验助推段的弹道优化,需要更多考虑的是在满足试验窗口的前提下尽量降低飞行环境的恶劣程度,尽量降低飞行过程中的最大动压、最大法向过载、攻角范围等参数,而不是单纯的能量最优、时间最短或总加热量最小等单一的优化目标。这样的优化目标在以前的弹道设计中不曾提及,因此,需要研究这种特殊的弹道优化问题。

1　弹道优化方法

1.1运动方程及优化目标

本文采用铅垂面内的三自由度模型,运动方程组为[16-17]

(1)

(2)

(3)

式中:FP为助推器推力;FX,FY分别为气动阻力和升力;α为飞行攻角;θ为弹道倾角;MZ为气动质心矩;ωZ为绕质心的俯仰角速度。

终端条件为助推段结束时分离时刻的试验窗口参数:

hend=hq+hΔ

(4)

Maend=Maq+MaΔ

(5)

θend=θq+θΔ

(6)

αend=0+αΔ

(7)

(8)

以上为理论弹道的5个终端条件,其中,h为飞行高度,Ma为飞行马赫数,下标“Δ”表示允许的偏差,下标“end”表示助推段结束时刻的弹道参数,下标“q”表示试验窗口要求的期望值。其中,试验模型质量参数、试验模型气动性能、助推器推力特性为已知条件。优化目标可以描述为

ny,max|0≤t≤tend=ny,min

(9)

pmax|0≤t≤tend=pmin

(10)

|α|max|0≤t≤tend=αmin

(11)

(12)

|α|max|0.8≤Ma≤1.5=αk,min

(13)

1.2优化算法

本文采用遗传算法对上述三自由度弹道进行优化。

1.2.1编码

编码是遗传算法的基础,本文提出了一种有理数编码方案。在助推段上按顺序选取若干时间节点并组成一维数组t=(t1,t2,…,tn),其中t1=0,tn=tend,选取由每个节点时刻的飞行攻角值构成的一维数组α=(α1,α2,…,αn)为弹道个体的染色体,即基因序列。采用这种编码方案的理由是:

①终端条件方程(7)可以自动满足;

②可以直接判断一部分针对攻角的约束条件,若不满足约束,不必计算该条弹道,从而很简单地避免了“攻角超界”的情况;

③在三自由度弹道中,攻角为物理意义上的自变量,当攻角历程确定后可以直接得到完整的弹道,若选取其他参数作为控制对象,比如弹道倾角或飞行高度等参数,都需要通过迭代计算出攻角值,无疑增加了计算复杂度。

④在工程应用中很少选用攻角作为控制对象,其主要原因在于干扰的存在和攻角测量的精度不足。但理论弹道设计不存在这样的情况。

1.2.2插值函数

仅有节点时刻的攻角值是不够的,需要进行插值计算。插值的方法很多,通常有线性插值、多项式插值、样条插值等方法。本文采用三次样条插值,理由如下:

①终端条件方程(8)可以自动满足;

②算法易于实现,当节点个数较多时,采用多项式插值时,方程的求解较为困难;

③通过样条插值得到的攻角历程是一条光滑的曲线,而不是线性插值得到的一条折线,这更有利于后期的飞行控制系统设计工作。

1.2.3适应值函数

适应值是对染色体(个体)进行评价的一种指标,是GA进行优化作用的主要信息。在生物界中,对生存环境适应程度较高的物种或个体将有更多的繁殖机会,反之则机会较少,甚至灭绝。与之类似,遗传算法也使用适应度这个概念来量度种群中各个个体在优化计算中有可能达到或接近于或有助于找到最优解的优良程度。

适应值函数通常是由优化的目标函数变换而成的。本文提出了一种将优化过程划分为2个阶段的方法:首先搜索满足终端条件的可行解,然后在可行解的基础上搜索飞行环境恶劣程度更小的弹道。2个阶段的适应值函数分别为

A1=|hend-hq|k1+|Maend-Maq|k2+|θend-θq|k3

(14)

(15)

式中:k1,k2,…,k8为人为设定的正系数。针对第2阶段的适应值函数A2,需要增加惩罚函数,确保满足试验窗口条件。值得一提的是,上述适应值函数应取极小值为优化目标。

在实际计算过程中,系数的确定还需要考虑各项参数本身的物理意义。比如,若分离点高度与终端条件偏差10 m,或者动压偏差1 kPa,是完全可以接受的,但是弹道倾角与窗口条件即使仅偏差0.1 rad,就无法接受了。在确定以上系数时应充分考虑这一点。

2　算例

本文研究的算例采用固体火箭发动机为助推动力,从试验场地垂直发射(海拔高度约为1 km),并要求助推结束时进入飞行试验窗口。助推段飞行时间约为86 s,选取时间节点的间隔为2 s,即扣除初始和终端时刻的攻角为已知后,实际参与编码的基因为42个。采用的种群大小为100,选择概率为0.9,并保留5%的最优个体,变异概率为0.05,种群初值为全程零攻角飞行。图2～图7给出了最终弹道参数曲线。

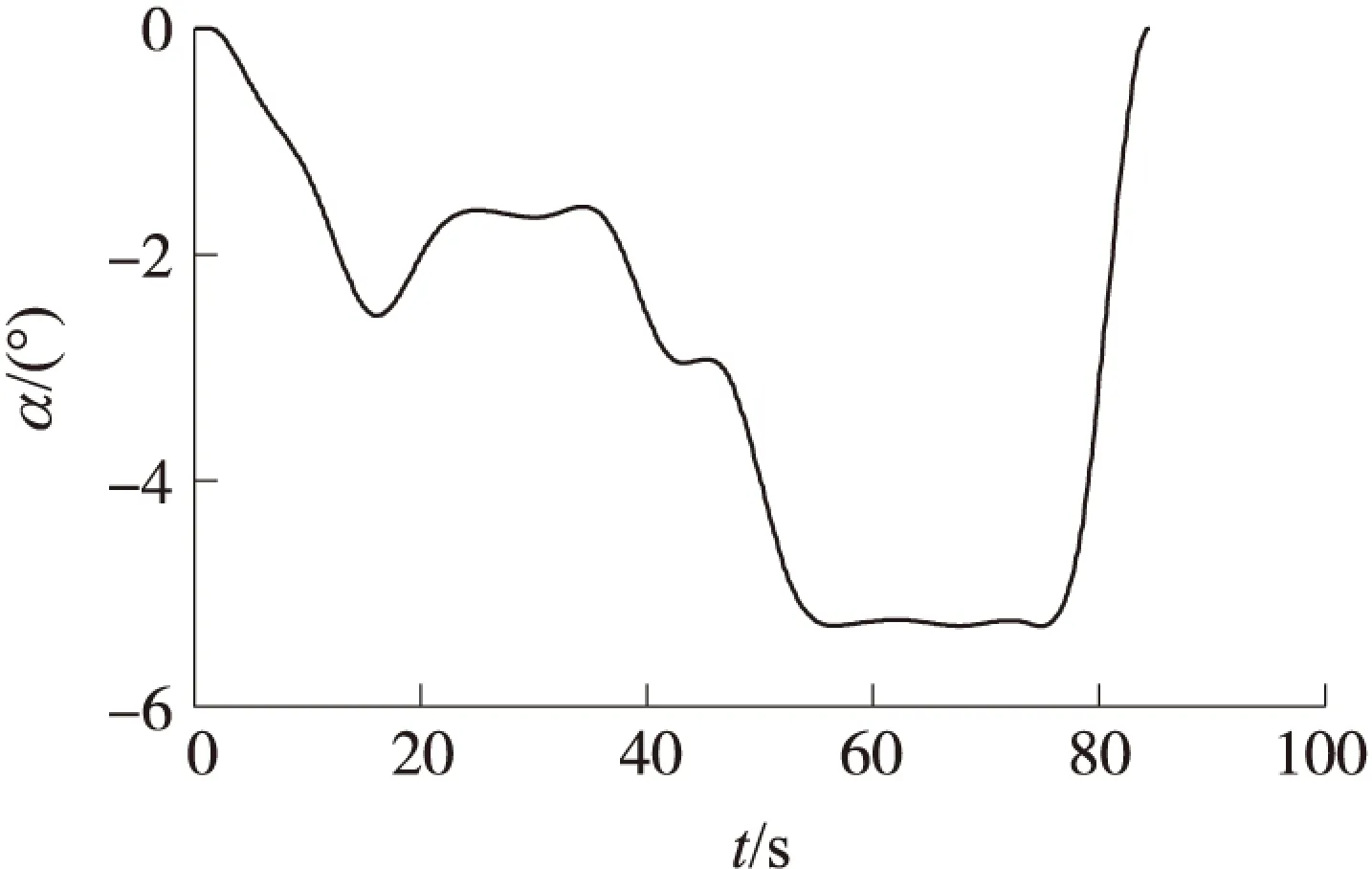
图2　攻角随时间变化曲线

从图2可知,试验模型的助推段全程为负攻角飞行。在助推段后期,助推火箭发动机进入拖尾段之前的一段较长时间范围内,试验模型保持-5.3°左右的最大负攻角飞行。这样的飞行方式既充分利用负升力来调整飞行的弹道倾角,同时又避免了局部出现大攻角的情况,从而降低了最大法向过载和纵向配平舵偏,达到了减小飞行环境恶劣程度的优化目标。助推器熄火之前8 s,开始将攻角逐渐调整为0°以满足头体分离对姿态的要求。从图3可知,跨声速段出现在弹道的第23 s到第36 s之间,期间的攻角约为-1.6°。图4给出了飞行高度h及纵向配平舵偏角δZ随时间的变化曲线。由图可知：助推结束时,飞行高度约为25 km；最大舵偏角约为4°。后期的仿真分析表明,全助推段弹道可控,且有较大的控制裕度。

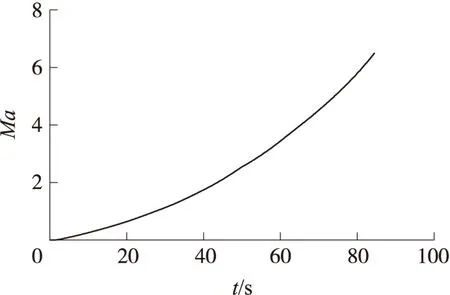
图3　飞行马赫数随时间变化曲线

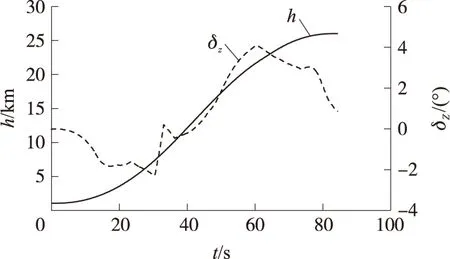
图4　飞行高度及纵向配平舵偏角随时间变化曲线

图5为动压p和法向过载ny随时间的变化规律。由图可知,最大动压约为100 kPa,且在助推段出现了2次,分别是低马赫数低空阶段和高马赫数高空阶段。在通常情况下,助推弹道动压曲线的这2个峰值是不相等的。其中,由于受到试验窗口参数的限制,高马赫数高空阶段的动压峰值变化范围不会太大。当低马赫数低空阶段的动压峰值大于高马赫数高空阶段的动压峰值时,需要调整助推段的攻角历程,以减小低马赫数低空阶段的动压峰值。调整的结果导致弹道在40 s附近时出现攻角曲线的微小波动。这种现象避免了局部出现高动压的情况,体现了弹道优化的结果。法向最大过载约为2.2g,出现在进入试验窗口前即将开始调整姿态的时刻。

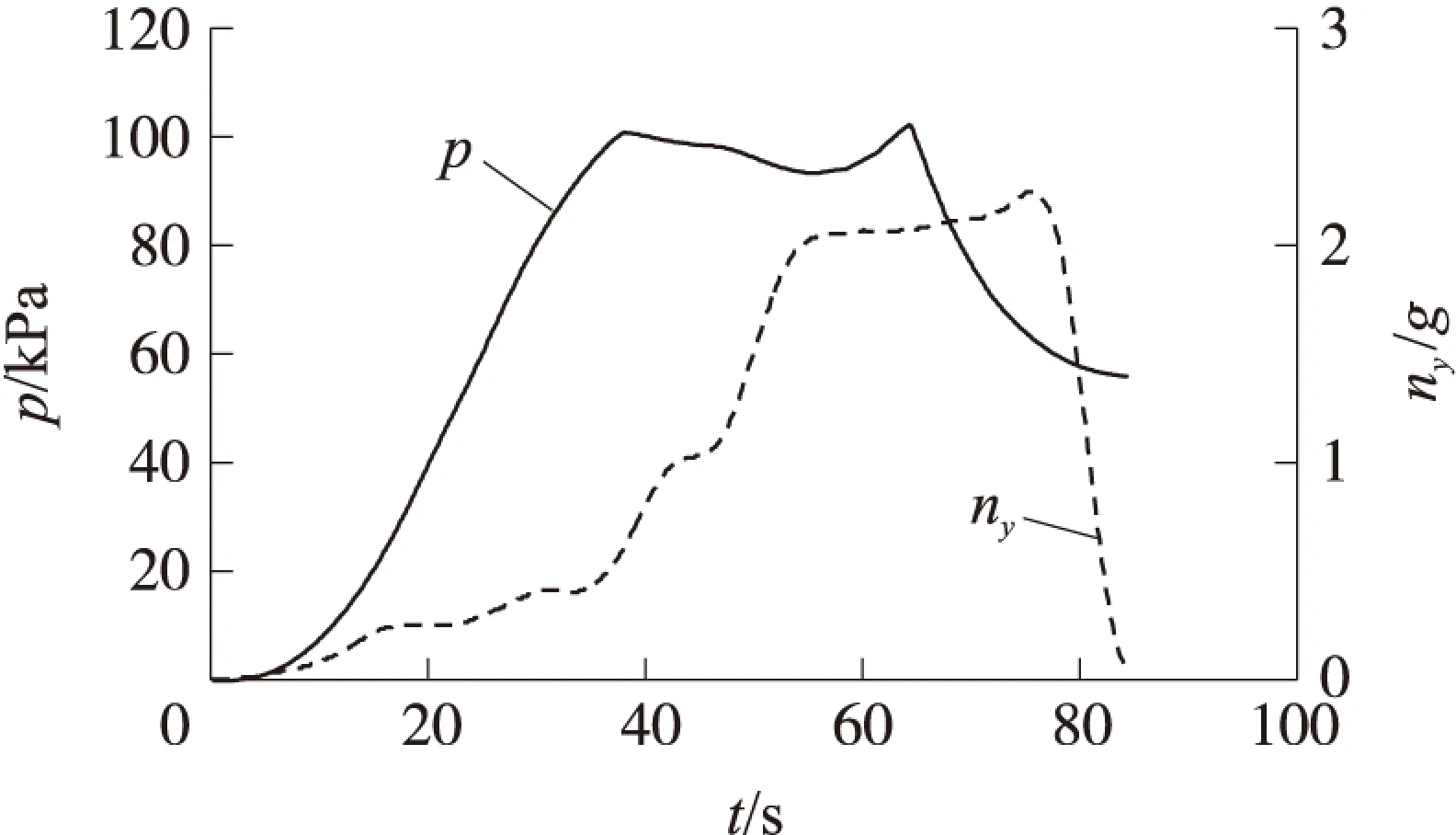
图5　飞行动压及法向过载随时间变化曲线

图6给出了改变种群的初始值对计算结果的影响。将各个节点的初始攻角统一设为±1°以及±2°,该优化算法均能最终达到与上述弹道基本一致的结果,这表明本文采用的优化算法并不依赖于计算初值,算法具有较好的鲁棒性。

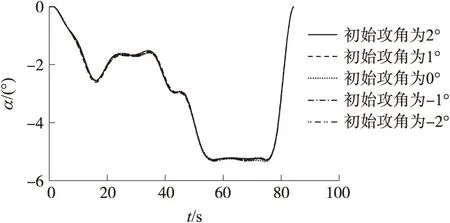
图6　不同初值的攻角计算结果

3　结论

本文采用遗传算法对高超声速飞行试验的助推段弹道进行了优化。结论如下:

①以试验窗口参数为约束条件,以降低飞行环境的恶劣程度为弹道优化的目标,可以既满足试验窗口条件,又最大限度地降低助推段的最大攻角、最大飞行动压、最大法向过载,从而降低气动布局、操稳特性、结构强度等分系统的设计难度。

②采用该算法得到的理论弹道,结果合理,且算法不依赖计算初值,具有良好的鲁棒性。

[1]甘楚雄,刘冀湘.弹道导弹与运载火箭总体设计[M].北京:国防工业出版社,1996.

GAN Chu-xiong,LIU Ji-xiang.Ballistic missiles and launch vehicles design[M].Beijing:National Defense Industry Press,1996.(in Chinese)

[2]龙乐豪.导弹与航天丛书:总体设计[M].北京:中国宇航出版社,1991.

LONG Le-hao.Missile and space series:overall design[M].Beijing:China Astronautic Publishing House,1991.(in Chinese)

[3]JOSEPH M H.The X-51A scramjet engine flight demonstration program,AIAA 2008-2 540[R].2008.

[4]何献忠,李萍.优化技术及其应用[M].北京:北京理工大学出版社,1995:12-156.

HE Xian-zhong,LI Ping.Optimization technique and applications[M].Beijing:Beijing Institute of Technology Press,1995:12-156.(in Chinese)

[5]方洋旺.随机系统最优控制[M].北京:清华大学出版社,2005.

FANG Yang-wang.Stochastic system optimal control[M].Beijing:Tsinghua University Press,2005.(in Chinese)

[6]张光澄.非线性最优化计算方法[M].北京:高等教育出版社,2003.ZHANG Guang-cheng.Computational methods for nonlinear optimization[M].Beijing:High Education Press,2003.(in Chinese)

[7]HARADA A.Dynamic programming trajectory optimization by piecewise linear approximation,AIAA 2015-1 075[R].2015.

[8]MIYAZAWA Y.Dynamic programming application to airliner four dimensional optimal flight trajectory,AIAA 2013-4 969[R].2013.

[9]DAI R.Three-dimensional minimum-time interception trajectory planning using nonlinear programming and collocation,AIAA 2007-6 787[R].2007.

[10]郑总准,吴浩,王永骥.基于序列二次规划算法的再入轨迹优化研究[J].航天控制,2009,27(6):8-13.

ZHENG Zong-zhun,WU Hao,WANG Yong-ji.Reentry trajectory optimization using sequential quadratic programming[J].Aerospace Control,2009,27(6):8-13.(in Chinese)

[11]刘欣,杨涛,张青斌.助推-滑翔导弹弹道优化与总体参数分析[J].弹道学报,2012,24(1):43-48.

LIU Xin,YANG Tao,ZHANG Qing-bin.Trajectory optimization and parameter analysis for boost-glide missile[J].Journal of Ballistics,2012,24(1):43-48.(in Chinese)

[12]傅瑜,马永青,崔乃刚.可重复使用助推飞行器轨迹优化研究[J].弹道学报,2011,23(4):5-9.

FU Yu,MA Yong-qing,CUI Nai-gang.Research on optimal trajectory of reusable boost vehicle[J].Journal of Ballistics,2011,23(4):5-9(in Chinese)

[13]王凌.智能优化算法及其应用[M].北京:清华大学出版社,2001:36-59.WANG Ling.Intelligent optimization algorithms with applications[M].Beijing:Tsinghua University Press,2001:36-59.(in Chinese)

[14]齐照辉,梁伟,刘雪,等.弹道导弹助推段突防多目标优化设计方法[J].弹道学报,2010,22(2):39-43.

QI Zhao-hui,LIANG Wei,LIU Xue,et al.Multiobjective optimization algorithm of survivability of ballistic missile in boost phase[J].Journal of Ballistics,2010,22(2):39-43.(in Chinese)

[15]杨遵,雷虎民,唐治理.基于作战效能的无人机航路规划研究[J].电光与控制,2009,16(11):14-18.

YANG Zun,LEI Hu-min,TANG ZHI-li.Combat effectiveness based path planning for unmanned air vehicles[J].Electron Optics & Control,2009,16(11):14-18.(in Chinese)

[16]韩子鹏.弹箭外弹道学[M].北京:北京理工大学出版社,2008.

HAN Zi-peng.Exterior ballistics of projectile and rocket[M].Beijing:Beijing Institute of Technology Press,2008.(in Chinese)

[17]王中原,周卫平.外弹道设计理论与方法[M].北京:科学出版社,2004:59-102.

WANG Zhong-yuan,ZHOU Wei-ping.Theory and method of exterior ballistic design[M].Beijing:Science Press,2004:59-102.(in Chinese)

Investigation on Boost Trajectory Optimization Method of Hypersonic Flight Test

ZHANG Zi-ming,JIANG Jin,WANG Xi-yao

(Science and Technology on Scramjet Laboratory,Hypervelocity Aerodynamics Institute,CARDC,Mianyang 621000,China)

To reduce the badness of the flight environment of the boost phase in the hypersonic flight test,a novel optimization method to generate 3-DOF optimal trajectory was proposed.The method based on the angle of attack(AOA)encoding genetic algorithm was adopted,and the cubic spline was employed to smooth attack angle time courses.During the optimization process,the feasible solution was first searched to meet window parameters.Then the optimal trajectory with the lowest badness of flight environment was searched for the objective functions such as attack angle range,the maximum dynamic pressure and the maximum normal overload parameters under the constraint of the windows parameters.The results show that the algorithm can avoid the local high risk in the theoretical trajectory,and it has good robustness.

hypersonic vehicle;theoretical trajectory;genetic algorithm;multi-objective optimization

2016-03-05

张子明(1974- ),男,高级工程师,研究方向为飞行试验技术。E-mail:fatmanzzm@sina.com。

TJ013

A

1004-499X(2016)03-0012-05