红外图像末制导炸弹全弹道捕获区域快速解算方法

庞　威,谢晓方

(海军航空工程学院 兵器科学与技术系,山东 烟台 264001)



红外图像末制导炸弹全弹道捕获区域快速解算方法

庞威,谢晓方

(海军航空工程学院 兵器科学与技术系,山东 烟台 264001)

为实现红外图像末制导炸弹全弹道捕获区域的快速计算,通过分析导引头的瞬时捕获域条件,以导引头中轴线为中心,利用坐标变换建立了红外图像末制导炸弹的瞬时捕获域模型;给出了不同视场角的瞬时捕获域形状,在此基础上提出了红外图像末制导炸弹的全弹道捕获区域快速计算方法。分析了全弹道捕获域的过程,假设炸弹飞行过程中弹道倾角不变,分别给出了采用平台型导引头和捷联型导引头的红外图像末制导炸弹全弹道捕获区域的快速计算方法。分别对采用追踪制导律和大落角制导律的某型红外图像制导炸弹的全弹道捕获区域进行了仿真分析,结果表明,提出的快速计算全弹道捕获区域与仿真结果误差较小,可用于红外图像末制导炸弹全弹道捕获区域的快速计算。

红外图像制导炸弹;导引头;瞬时捕获域;全弹道捕获域

新型远程红外图像末制导炸弹是在普通航弹基础上加装被动式红外成像导引头,以实现防区外投放,并根据导引头所成的红外图像来自动搜索、识别、捕获和攻击目标,其导引头可分为平台式和捷联式。平台式导引头安装在稳定的平台上,隔离弹体运动对其产生的影响。捷联式导引头与弹体固连,通过坐标变换实现视线稳定跟踪,降低了成本,提高了可靠性。新型远程红外图像末制导炸弹可实现防区外投放,射程远,打击精度高,但由于战场中目标的运动特性,需要较大的捕获区域以确保对目标的精确捕获。因此,研究制导炸弹的全弹道捕获区域,对新型制导炸弹的指标论证具有重要意义。

相关文献研究了不同类型导引头的捕获区域。文献[1]以地面固定目标为例,利用导引头光轴坐标系和导引头平动坐标系之间的转换关系,建立了激光半主动末端脉冲修正弹的探测区域模型,指出了影响捕获区域的相关因素。文献[2]利用相对性原理的思想建立了末端寻的制导反坦克导弹捷联式导引头的捕获域模型,并分析了各种因素对捕获域的影响,但只分析了平飞弹道的捕获区域,没考虑高度对捕获区域的影响。文献[3]建立了风标弹和比例弹有风和无风时的捕获区域模型,并采用等效视场方法分析了2种弹的捕获概率,结果表明两者捕获域近似相同。文献[4]通过建立导引头地面捕获区域,以理想弹道作为名义捕获区域中心,根据其与真实目标位置的相对差来修正射表投弹的距离,并研究了驾驶仪过载和攻角对导引头捕获目标概率的影响。文献[5]建立了激光末制导炮弹的瞬时捕获区域,分析了瞬时捕获域的边界随炮弹运动的关系,求解了全弹道捕获区域,并对影响捕获域的各种因素进行了仿真分析。

以上文献研究的均是激光或者雷达制导导引头,针对红外图像末制导导引头的全弹道捕获区域研究较少。与激光或雷达导引头在地海平面的瞬时捕获区域为椭圆不同,某新型红外导引头采用凝视焦面阵成像技术,在地海平面的瞬时捕获区域为梯形[6]。因此,本文以某新型远程红外图像末制导炸弹为应用背景,以坐标变换关系为基础,建立了导引头视场角的瞬时捕获域模型;以此为基础,假设弹道倾角不变,建立了不同类型导引头的全弹道捕获区域快速解算模型,并进行了仿真实验。

1　瞬时捕获区域的建模

1.1相关坐标系以及转换关系

涉及到的坐标系主要有2个:导引头中轴坐标系和目标点所在的水平面坐标系,如图1所示。

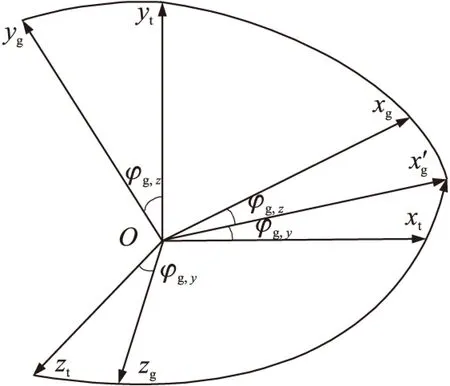
图1　导引头中轴坐标系与目标点所在水平面坐标系的关系

①导引头中轴坐标系的定义。以导引头的中心点为原点O,Oxg轴指向导引头中轴方向,沿导引头前方为正;Oyg轴在炸弹运动纵向平面内与Oxg轴相互垂直,指向上方为正;根据右手坐标系规则确定Ozg轴。

②目标点所在水平面坐标系的定义。以目标所在位置为原点O,Oxt轴在目标运动的横向平面内,向右为正;Oyt轴在目标运动的纵向平面内与Oxt轴相互垂直,指向上方为正;根据右手坐标系规则确定Ozt轴。

导引头的俯视角φg,z:导引头的中轴与Oxtzt平面所成的夹角,规定俯视角φg,z的正方向为导引头中轴指向Oxtzt平面上方,反之则为负。

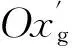
根据上述2个坐标系的定义,可通过导引头的俯视角φg,z和侧视角φg,y来确定两者之间的转换关系,其转换矩阵为

I(φg,z,φg,y)=

(1)

则炸弹在Oxtytzt坐标系中的位置为

(xgygzg)T=I(φg,z,φg,y)(xtytzt)T

(2)

1.2导引头的瞬时捕获区域

红外图像末制导炸弹在弹道末段搜索、探测、识别和捕获目标,为研究方便,不考虑目标搜索、探测和捕获的时间,则导引头在水平面内的瞬时捕获区域如图2所示。假设导引头中轴即为导引头的光轴,且在解锁前与炸弹弹体纵轴方向重合,导引头的纵向视场角(纵向平面内导引头中轴和最大视场之间的夹角)为ψa,横向视场角(横向平面内导引头中轴和最大视场之间的夹角)为ψb,弹道倾角为q,攻角为α,炸弹距离水平面的高度为h。由图2所示的几何关系可知,以导引头启控点为顶点,形成的锥体与目标所在水平面相交所形成的区域为梯形。同时,以导引头启控点为球心,以导引头的作用距离R为半径的球与目标所在的水平面相交所成的区域为圆,本文称之为作用圆;梯形与作用圆相交的区域即为导引头的瞬时捕获区域。由于炸弹所处的高度和导引头的视场角不同,瞬时捕获区域可能为整个梯形或部分梯形与作用圆共同围成的区域[7-8]。显然,导引头的瞬时捕获区域与导引头的视场角(纵向和横向视场角)、导引头的作用距离、炸弹的高度、弹体姿态角(攻角、侧滑角和弹道倾角)等因素有关。其中,红外图像导引头的有效作用距离又和大气温度、颗粒散射以及导引头的灵敏度等因素有关。

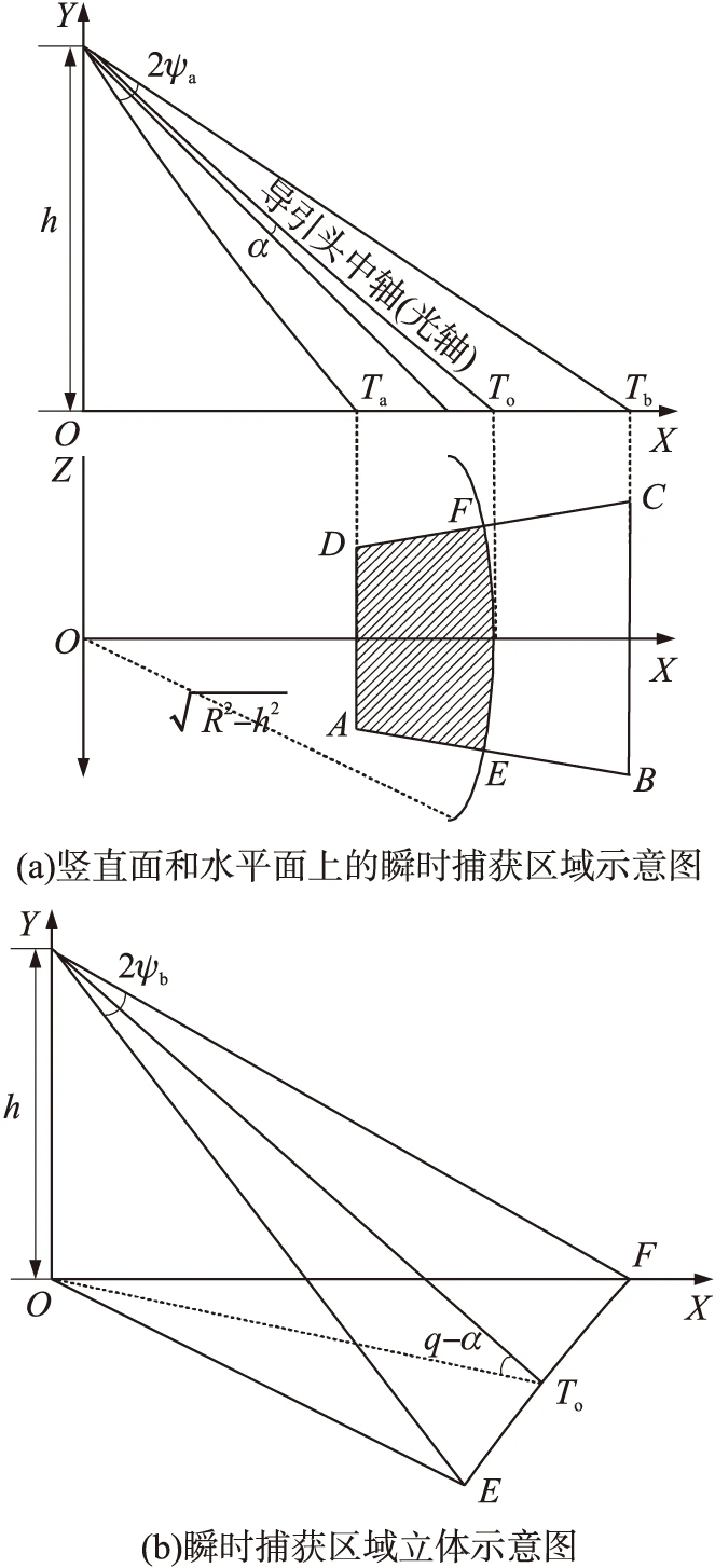
图2　导引头的瞬时捕获区域示意图

从图2中可得出:梯形的高为TaTb，与导引头的纵向视场角相关,E和F为导引头横向方向与地面作用圆之间的交点,与导引头的横向视场角相关。若炸弹的弹道倾角和攻角固定,那么导引头的瞬时捕获区域与炸弹的高度和导引头的视场角正相关,且纵向视场角越大,梯形的高度就越大,导引头捕获预装定目标点的近区和远区的能力也就越强;炸弹的瞬时飞行高度越高,导引头瞬时捕获预装定目标点的远区能力就越强,捕获预装定目标点近区的能力就越弱。同理,当炸弹飞行高度和攻角保持不变时,弹道倾角越大,锥体与水平面中目标点的作用圆重合区域越大,捕获预装定目标的能力就越强,反之,捕获预装定目标的能力就越弱。捕获预装定目标能力随攻角的变化情况与弹道倾角的情况相反。

当炸弹高度低于一定的高度后,其瞬时捕获区域随着高度的降低将减小。当弹目距离较近时,由于其瞬时捕获区域被在高处的瞬时捕获区域所覆盖,因此设定当高度低于某一特定值后捕获结束。

1.3导引头瞬时捕获区域的建模

在红外图像末制导炸弹攻击目标的过程中,导引头的瞬时捕获区域为瞬时视场在目标所在水平面的瞬时投影[9]。在导引头中轴坐标系下的瞬时捕获区域应满足:弹目的最大距离应小于导引头的捕获距离;弹目之间的视线角应小于导引头视场角的约束[3]。与激光制导炸弹的瞬时捕获域不同,红外图像末制导炸弹的视场角分为纵向视场角和横向视场角。在导引头中轴坐标系下的捕获区域的边界需满足以下方程:

(3)

式中:ψa,ψb分别为导引头的纵向和横向视场角。

设炸弹在目标点水平面坐标系的坐标为M(xm,ym,zm),目标点的坐标为T(xt,yt,zt),根据坐标转换关系,则线段MT在导引头中轴坐标系中的位置为

(4)

将式(2)、式(3)带入式(4)中,可得在目标点所在的水平面坐标系下的瞬时捕获区域:

(5)

为分析问题方便,不妨设炸弹在纵向平面内运动,目标位于水平面内,即有:ym=h,zm=0,yt=0,φg,y=0;方程(5)可化简为

(6)

式(6)中第3式表示的即为作用圆。从式(6)中可以看出,导引头的瞬时捕获区域为4条直线围成的区域与作用圆相交重合的区域。根据φg,z,ψa,ψb的取值,可将围成的区域分为以下几种情况。

①φg,z>ψb且φg,z>ψa时,导引头的瞬时捕获区域为一梯形与圆相交的区域,即梯形位于圆中的区域,如图3(a)所示。

②ψb>φg,z且φg,z>ψa时,导引头的瞬时捕获域为梯形左侧边与圆围成的右侧区域,即圆中位于梯形内的部分,如图3(b)所示。

③ψa>φg,z且ψb>φg,z时,导引头的瞬时捕获域与情况②相同,只是导引头视场在地面的投影是梯形去除了底边,如图3(c)所示;其他情况类似。

图3　3种类型的瞬时捕获区域

在实际应用过程中,导引头误差角通常小于弹道倾角,本文以第①种情况为例,研究炸弹导引头的全弹道捕获区域,其他情况也可采用类似的方法处理。

2　全弹道捕获区域

2.1全弹道捕获区域分析

红外图像末制导炸弹的全弹道捕获区域是指末制导炸弹在攻击目标的过程中能够对目标所在水平面进行捕获的所有分布区域,该过程从攻击预装定目标位置的信息时刻开始,到接收到目标信息但无法继续进行导引的时刻结束[5]。

某一时刻的瞬时捕获区域情况有3种:①炸弹位置较高,导引头作用距离较短,以炸弹所在位置为球心,以导引头的作用距离为半径的球与目标所在的平面不相交,此种情况的捕获域为零。②图3(a)中情况在搜索过程中较为常见,随着弹目距离的不断减小,以导引头为球心、作用距离为半径的球与水平面相交的区域不断增大,导引头在目标所在平面的瞬时捕获域的完整性也不断加大,之后覆盖整个导引头的捕获域。③当炸弹飞行高度较低时,导引头在地面的瞬时捕获区域随着飞行高度的降低不断减小,同时投影区域逐渐进入以导引头为球心、作用距离为半径的球与水平面相交的作用圆内。其捕获过程如图4所示。

图4　导引头的捕获过程

已知某新型远程红外末制导炸弹采用SINS/BD(Beidou,BD)中制导+红外图像末制导方式,分别研究采用平台导引头和捷联导引头的全弹道捕获区域,进而确定采用末制导导引头的类型。

2.2平台式导引头的全弹道捕获区域

对于采用平台式导引头的红外图像末制导炸弹,在中制导捕获目标之前,炸弹弹体速度方向指向预装定的位置。在捕获目标之前,保持炸弹飞行速度方向基本不变,不考虑弹体的滚转和侧滑运动。因此,对于采用此种导引头的红外图像末制导炸弹,在中制导时,通过调整导引头的框架角指令可使导引头的中轴始终指向射前预装定目标的位置。此时炸弹的弹道倾角q等于导引头的俯视角,即q=φg,z。

由上述分析知,炸弹飞行捕获过程中的弹道倾角保持不变,则

h=xmtanq

(7)

根据式(6)中第2式和第3式联立求解出梯形与作用圆的交点坐标:

(8)

式中:

将式(7)带入到式(8)中,消去xm,可得:

(9)

式(9)为以导引头有效作用距离R为长半轴,Dp为短半轴的椭圆,记为SE。

同理,将式(6)中第1式和第3式联立求解,得到梯形的2条腰与作用圆的交点的轨迹方程:

(10)

所以式(10)表达的是长半轴为Ep,短半轴为Fp的椭圆,记为PE。

则采用平台导引头的制导炸弹全弹道捕获区域是以目标点为中心,式(9)和式(10)的2个椭圆相互重合围成的区域。

2.3捷联导引头的全弹道捕获区域

当某新型红外图像末制导炸弹采用捷联导引头时,捕获预装定目标前导引头与弹体固连,导引头中轴方向与炸弹弹体纵轴方向相同,则炸弹的俯仰角与导引头视线角相等。因此,在炸弹飞行的纵向平面内有:

φg,z=q+α

(11)

式中:α为攻角。攻角的产生导致其捕获区域不再关于预装定目标点对称,因此根据式(8)和式(6)中第2式可得捷联导引头的全弹道捕获区域:

(12)

式中:

以及,

(13)

式中:

为下文表示方便,记式(12)和式(13)分别为椭圆SE1和SE2。

同理,将式(6)中第1式和第3式联立求解,得出梯形的两条腰与作用圆的交点的轨迹方程:

Ds1x2+Es1xz+Fs1z2-Gs1=0

(14)

式中:

根据文献[10],令

显然,I1>0;且

tan2α+cos2φg,z+2sinφg,zcosφg,ztanq+sin2φg,ztan2q]

显然,I2>0,I1I3<0;故式(13)表示的是椭圆。

Ds2x2+Es2xz+Fs2z2-Gs2=0

(15)

式中:

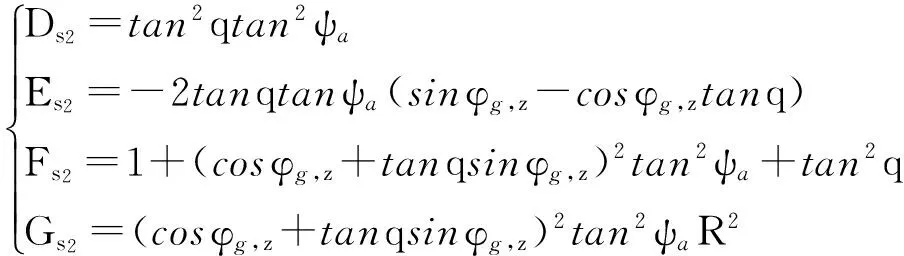
同理可证式(15)表示的也为椭圆。

捷联导引头的全弹道捕获区域为椭圆SE3和椭圆SE1所围成的公共区域加椭圆SE3和椭圆SE2围成的公共区域。

3　捕获区域的仿真计算

根据文献[11],某新型远程红外图像末制导炸弹的投放条件如下:载机的投放高度为10km,弹目初始距离60km,载机速度为250m/s(载机速度与炸弹的初始速度相同),载机的速度方向为0°(载机速度方向为炸弹的初始弹道倾角),红外图像导引头的有效作用距离为4km,纵向和横向视场角分别为15°和20°,炸弹的平衡攻角为-3°～+3°。载机投放炸弹后,炸弹展开弹翼滑翔飞行,采用“SINS/BD中制导机动+红外图像末制导”方案攻击目标,根据预装定的目标点坐标,采用追踪制导律引导炸弹飞向目标。当导弹到达导引头的启控点后转入末制导段。为提高捕获目标的概率,设定炸弹速度方向始终对准预装定目标点位置。

仿真中取末制导段弹道倾角为-30°,弹目距离为6km,采用Runge-Kutta法实时求解仿真弹道。

3.1末制导全弹道捕获区域仿真

图5、图6和表1分别表示某新型远程红外图像制导炸弹采用平台式导引头和捷联导引头全弹道捕获区域的快速计算理论结果和仿真结果;图5(b)和图6(b)是将重合区域放大的结果。表1中，c为横向捕获区域，ec为估计误差。

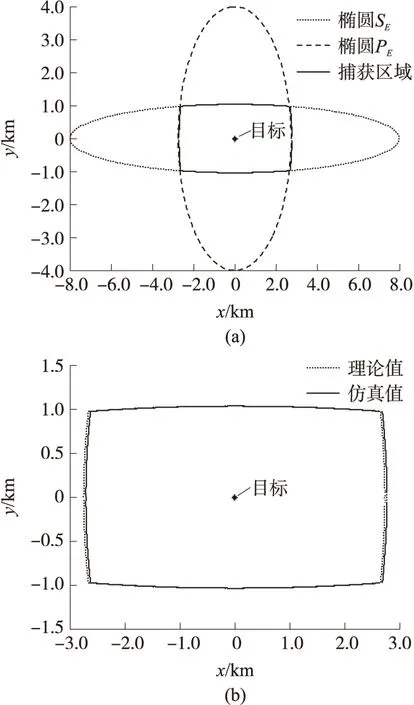
图5　平台式导引头全弹道捕获区域仿真

图6　捷联导引头捕获区域仿真

从表1中可以看出，平台式导引头和捷联导引头侧向捕获区域的理论值和仿真值的误差ec分别为0.051%和0.21%,这是由于侧向捕获区域的最大值只与导引头的作用距离和横向视场角有关,与飞行弹道倾角无关。同时,炸弹攻角的变化导致捷联导引头的侧向捕获误差大于平台式导引头的侧向捕获误差。

表1　横向捕获区域对比表

表2和表3给出了同等条件下平台式导引头和捷联导引头的纵向全弹道捕获区域的最大值、最小值和误差值,表中,lmax为纵向捕获区域的最大值，lmin为纵向捕获区域最小值,elmax,elmin为相应的估计误差。从表1、表2和表3中可以看出，文中的快速计算结果与仿真结果误差较小。

表2　纵向捕获区域最大值对比表

表3　纵向捕获区域最小值对比表

3.2大落角全弹道捕获域的仿真

为保证对目标的毁伤效果,远程红外图像末制导炸弹通常需要较大的落角以满足对目标的侵彻效果[12-13]。因此在弹道末端一般采用大落角末制导律,捷联导引头只能通过调整弹道倾角实现其大落角,对于平台式导引头则可通过调整框架角指令始终使导引头中轴对准目标。

显然,采用大落角末制导律时,由于炸弹飞行过程中弹道倾角的变化,不可采用第2节的公式计算炸弹的全弹道捕获区域,但可以通过这些公式来估计捕获区域的大致区域,可将捕获过程分成两部分。第一部分在炸弹捕获到目标前,按照等弹道倾角飞行,当捕获到目标时,根据3.1节分析知此时导引头的捕获区域的侧向最大。第二部分为导引头捕获到目标后,炸弹按照大落角末制导律飞行,此时,炸弹倾角的变化规律可选择为[14]

(16)

式中:q为炸弹的弹道倾角,qm,s为炸弹捕获到目标前的弹道倾角,D为弹目距离,Dm,s为炸弹恰好捕获到目标时弹目距离,qf为炸弹的最终落角。

图7和图8给出了落角分别为-70°和-90°时的全弹道捕获区域的理论值和仿真值,表4和表5给出了不同落角下纵向捕获区域的最大值和最小值。从图和表中可以看出,理论计算结果和仿真结果误差较小,因此可采用本文提出的方法对炸弹的全弹道捕获区域进行估算。

图7　-70°落角时的捕获区域

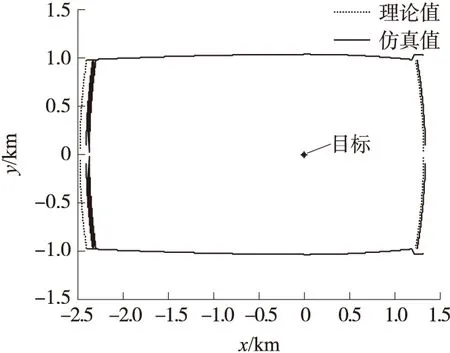
图8　-90°落角时的捕获区域

qf/(°)lmin/m理论值仿真值elmin/%-90-2397-23262.96-80-2397-23302.80-70-2397-23312.75-60-2397-23253.00

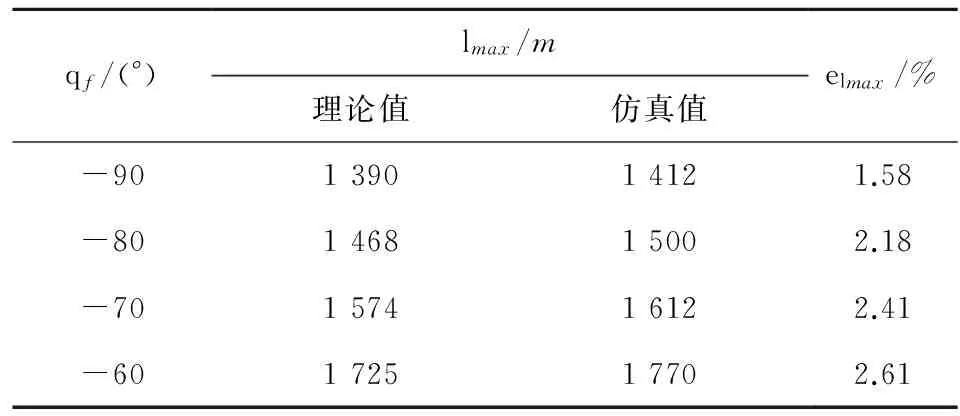
表5　不同落角时纵向捕获区域理论最大值和仿真最大值对比

4　结论

①导引头的全弹道捕获区域与炸弹的飞行高度无关。红外图像末制导导引头的全弹道捕获区域只与导引头的作用距离、纵向和横向视场角以及炸弹飞行过程中的弹道倾角有关,其中捷联导引头的捕获区域还与飞行攻角有关。导引头的纵向捕获区域只与导引头的作用距离和弹道倾角、纵向视场角成正比;横向捕获区域只与导引头的作用距离和横向视场角成正比,与弹道倾角和攻角无关。

②相同条件下,平台式导引头和捷联式导引头的横向捕获最大区域基本相同,由于攻角的影响,纵向捕获区域中捷联导引头相对于平台式导引头前移一段距离。

需要指出的是,虽然全弹道捕获区域与炸弹高度无关,但投放初始高度应大于导引头的作用距离,否则可能会导致捕获区域的初始值大于零,以至于全弹道捕获区域的理论值和仿真值产生较大误差。同时,全弹道捕获区域是一个静态的概念,捕获前采用弹道倾角不变的假设,对于时敏目标,不仅要考虑时间的约束,还要考虑目标所处的位置。因此,时敏目标的捕获区域还有待于进一步的研究。

[1]杨荣军,王良明,曹小兵,等.末段脉冲修正弹攻击区研究[J].弹箭与制导学报,2009,29(6):162-164.

YANG Rong-jun,WANG Liang-ming,CAO Xiao-bing,et al.Study on attack area for terminal correction projectile with impulse thruster control[J].Journal of Projectiles,Rockets,Missiles and Guidance,2009,29(6):162-164.(in Chinese)

[2]张西兴,谭亚莉,李小海.末段寻的制导的反坦克导弹捕获域研究[J].弹箭与制导学报,2003,24(4):25-26.

ZHANG Xi-xing,TAN Ya-li,LI Xiao-hai.A research on capture field for the terminal homing antitank missile[J].Journal of Projectiles,Rockets,Missiles and Guidance,2003,24(4):25-26.(in Chinese)

[3]夏群力,刘轶英,杨桂清.采用不同导引头的激光制导航弹捕获概率对比分析[J].系统仿真学报,2008,20(13):3 397-3 400.

XIA Qun-li,LIU Yi-ying,YANG Gui-ging.Comparison study of target acquisition probability between two types of laser guided bombs with different seekers[J].Journal of System Simulation,2008,20(13):3 397-3 400.(in Chinese)

[4]温求遒,崔莹莹,夏群利,等.基于导引头地面捕获域的激光制导炸弹射表修正技术[J].红外与激光工程,2012,41(8):2 053-2 057.

WEN Qiu-qiu,CUI Ying-ying,XIA Qun-li,et al.Firing table modifying based on acquisition ground zone of seeker for laser guidance bomb[J].Infrared and Laser Engineering,2012,41(8):2 053-2 057.(in Chinese)

[5]赵成旺,宋卫东,何伟.某型末制导炮弹全弹道捕获域研究[J].弹道学报,2013,25(2):54-58.

ZHAO Cheng-wang,SONG Wei-dong,HE Wei.Research on total capture area of terminal guidance projectile[J].Journal of Ballistics,2013,25(2):54-58.(in Chinese)

[6]张渊.舰载红外搜索跟踪系统的新体制研究[J].红外与激光工程,2009,38(4):583-588.

ZHANG Yuan.New scheme of ship-borne IRSTS[J].Infrared and Laser Engineering,2009,38(4):583-588.(in Chinese)

[7]杨桂清,夏群力,王林平.激光比例制导航弹对目标的捕获概率分析[J].弹箭与制导学报,2006,26(2):20-22.

YANG Gui-qing,XIA Qun-li,WANG Lin-ping.Study of target acquisition probability for laser-guided bombs with proportional navigation guidance law[J].Journal of Projectiles,Rockets,Missiles and Guidance,2006,26(2):20-22.(in Chinese)

[8]林德福,牟宇,常超,等.激光半主动末制导炮弹捕获概率研究[J].北京理工大学学报,2010,30(6):698-701,706.

LIN De-fu,MOU Yu,CHANG Chao,et al.A study of target acquisition probability for laser semi-active terminal guided projectile[J].Transactions of Beijing Institute of Technology,2010,30(6):698-701,706.(in Chinese)

[9]李兴隆,于纪言,姚文进,等.基于末段修正迫弹命中概率的射角优化[J].弹道学报,2014,26(2):90-94.

LI Xing-long,YU Ji-yan,YAO Wen-jin,et al.Optimization of launching angle based on hit probability for terminal correction mortar projectile[J].Journal of Ballistics,2014,26(2):90-94.(in Chinese)

[10]沈永欢,叶其孝.实用数学手册[M].北京:科学出版社,2006.

SHEN Yong-huan,YE Qi-xiao.Practical methematics handbook[M].Beijing:Science Press,2006.(in Chinese)

[11]袁宴波,张科,薛晓东.基于Radau伪谱法的制导炸弹最优滑翔弹道研究[J].兵工学报,2014,35(8):1 179-1 186.

YUAN Yan-bo,ZHANG Ke,XUE Xiao-dong.Optimization of glide trajectory of guided bombs using a Radau pseudo-spectral method[J].Acta Armamentarii,2014,35(8):1 179-1 186.(in Chinese)

[12]ZHANG You-an,MA Guo-xin,LIU Ai-li.Guidance law with impact time and impact angle constraints[J].Chinese Journal of Aeronautics,2013,26(4):960-966.

[13]TAUB I,SHIMA T.Intercept angle missile guidance under time varying acceleration bounds[J].Journal of Guidance,Control,and Dynamics,2013,36(3):686-699.

[14]窦磊,杨新民.大着地角卫星制导炸弹最优制导律研究[J].南京理工大学学报,2010,34(3):314-318.

DOU Lei,YANG Xin-ming.Optimal guidance law of satellite guided bombs with large landing angle[J].Journal of Nanjing University of Science and Technology,2010,34(3):314-318.(in Chinese)

Rapid Calculation Method for Total Capture Area of Infrared-image Terminal Guided Bomb

PANG Wei,XIE Xiao-fang

(Department of Ordance Science and Technology,Naval Aeronautical and Astrounautical University,Yantai 264001,China)

To rapidly calculate the total capture area of infrared-image terminal guided bomb(TGB),the condition of the instant capture area was analyzed,and the middle axis of the seeker was taken as center,and the instant capture area model was established by using coordinate transformation.The shape of instant capture area in different field of view was given.On this basis,the rapid calculation method of total capture area of infrared-image TGB was proposed.Under the assumption of the flight path angle keeping constant,the total capture area of the guided bomb with the gimbaled seeker and the strap-down seeker were put forward respectively.The total capture area for the infrared image TGB guided by tracking method and the large angle of fall guidance law was simulated,respectively.The results show that the total capture area by the rapid calculation is in agreement with the simulation result,and the rapid calculation can be used for the fast calculation of the total capture area of infrared-image TGB.

infrared-image guided bomb;seeker;instant capture area;total capture area

2016-05-23

庞威(1987- ),男,博士研究生,研究方向为武器系统建模与仿真。E-mail:metrix_yt@163.com。

谢晓方(1962- ),男,教授,博士生导师,研究方向为火力控制、红外技术。E-mail:xiexf106@yahoo.com.cn。

TJ414

A

1004-499X(2016)03-0035-08