初态误差对显式制导弹道导弹命中精度的影响特性

马宝林,张洪波,吴　杰

(国防科学技术大学 航天科学与工程学院,长沙 410073)



初态误差对显式制导弹道导弹命中精度的影响特性

马宝林,张洪波,吴杰

(国防科学技术大学 航天科学与工程学院,长沙 410073)

为研究初态误差对显式制导弹道的影响特性,在分析初态误差对标准弹道、实际飞行弹道影响机理的基础上,归纳推导了初态误差对导航和需要速度计算影响的分析模型，基于误差模型分析了初态误差对显式制导关机时间的影响机理。提出了初态误差对弹道和显式制导影响的分析方法,仿真分析了初态误差对不同地区同射向发射和相同地区不同射向发射的影响结果。仿真结果表明,在不考虑其他导航误差的情况下,初态误差对标准弹道和显式制导弹道的命中精度误差量在5%以内。

弹道导弹;地球扰动引力场;初态误差;显式制导;需要速度

地球扰动引力场对远程弹道导弹命中精度有显著的影响[1],影响因素包括飞行过程中的扰动引力和发射场区域扰动引力场两部分。其中,飞行过程中的扰动引力主要影响导弹的受力,问题的关键在于如何精确、快速确定飞行过程中导弹所受的扰动引力。近年来这方面的研究成果很多,例如:郑伟[1]提出了战场环境下的空间扰动引力快速赋值方法;张皞[2]推导了快速逼近弹道扰动引力的算法;李晓燕[3]区分主动段和被动段分析了扰动引力对弹道的影响结果等。

相比而言，发射场区域扰动引力场的影响比较复杂。考虑扰动引力场与否的影响，实质上体现的是垂线偏差对弹道导弹命中精度的作用。垂线偏差是影响导弹命中精度的重要因素[4]，这方面的研究文献较多，例如：文献[5]分析了原点垂线偏差对远程导弹定位结果产生影响的原因；文献[6]研究了存在垂线偏差的条件下惯性制导初始方位角出现误差的机理；文献[4,7]系统分析了垂线偏差对弹道导弹命中精度的影响。由于在不进行独立天文测量的情况下，天文坐标需要用大地坐标和垂线偏差计算得出，这时必然会引进垂线偏差的计算误差和大地坐标的测量误差。文献[1]推导了一种定位定向误差对显式制导精度的影响分析模型，该模型拥有解析解，运算速度快、精度高，但前提是需要进行独立的天文测量。为缩短发射准备时间，该假设条件在有些情况下无法满足。同时，初始定位定向误差的概念在导航、制导领域的界定也比较模糊，在许多导航误差模型中，仅将发射点大地经度、纬度和发射方位角作为初始定位定向误差考虑。为有所区别,将发射点垂线偏差的计算误差和大地测量误差统称为初态误差。初态误差主要影响导弹发射时的定向、定位。初始定向的误差源主要有两个：一是垂线偏差ξ、η的计算误差；二是方位角A0的测量误差。初始定位误差包括大地经度λ0、纬度B0和高程h0的测量误差。

基于此，本文首先分析了初态误差对标准弹道、实际飞行弹道和制导弹道的影响机理，指明了初态误差对显式制导弹道和标准弹道影响之间的区别；然后在不进行独立天文测量的前提下分析了初态误差对显式制导命中精度的影响特性，回答了初态误差如何对显式制导产生影响的问题。本文的研究对于揭示初态误差对显式制导的影响机理、提高远程弹道导弹命中精度具有重要的意义。

1　初态误差对标准弹道的影响机理

导弹系统一般采用发射惯性坐标系作为弹道制导计算用坐标系[8]。初态误差影响发射惯性坐标系的初始点位置和定向基准,使得整个导航计算框架发生了变化。同时初态误差还对弹道(导航)初值和飞行过程中的受力产生影响[1]。

如图1所示,弹道1是在考虑初态误差条件下迭代计算后得到的标准弹道;该弹道能从理想发射点准确击中目标点。弹道2是未考虑初态误差影响、按弹道1诸元计算的弹道;由于初态误差的影响,弹道2与弹道1计算用的坐标框架不一致,在标准关机时刻弹道2的飞行状态量与弹道1标准关机点状态量存在偏差,并由此使得落点偏离目标点。落点偏差ΔL1,Δh1为初态误差对标准弹道的影响结果。

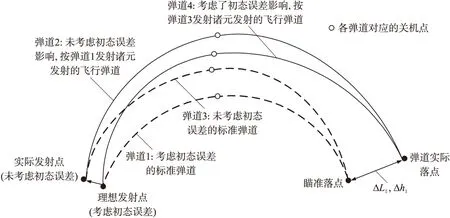
图1　初态误差对标准弹道的影响

2　初态误差对实际飞行弹道的影响机理

如图1所示,假设弹道3是在不考虑初态误差影响下迭代计算得到的标准弹道;弹道4考虑了初态误差的影响,实际飞行弹道将偏离标准弹道,在标准关机时刻,关机点状态存在偏差并由此产生落点偏差。弹道3、弹道4与弹道1、弹道2之间的落点偏差均是由于弹道计算坐标框架不一致产生的结果,而框架不一致的原因均是由初态误差引起的,所以弹道3、弹道4与弹道1、弹道2之间的落点偏差是相等的。

3　初态误差对显式制导弹道命中精度的影响机理

如图2所示,弹道5、弹道6为添加了显式制导的弹道。弹道5考虑了初态误差的影响,平台测量参数可直接用于导航计算,在不考虑其他导航误差源情况下,根据显式制导的原理,导弹能够准确命中目标;弹道6由于采用含有误差的飞行状态计算关机指令,关机指令会出现偏差进而影响到落点。落点偏差ΔL2,Δh2为初态误差对显式制导弹道的影响结果,具体可通过弹道6与弹道5之间的关机点状态误差与落点偏差之间的关系进行分析。

基于需要速度的显式制导是最常见的一种方法[9]。该方法通过需要速度进行导引、控制,当目标点参数固定时,当前时刻导航位置计算结果是确定需要速度的决定因素。所以,本部分就初态误差对导航、需要速度计算的影响分别进行研究,并在此基础上分析初态误差对关机点信号的影响特性。

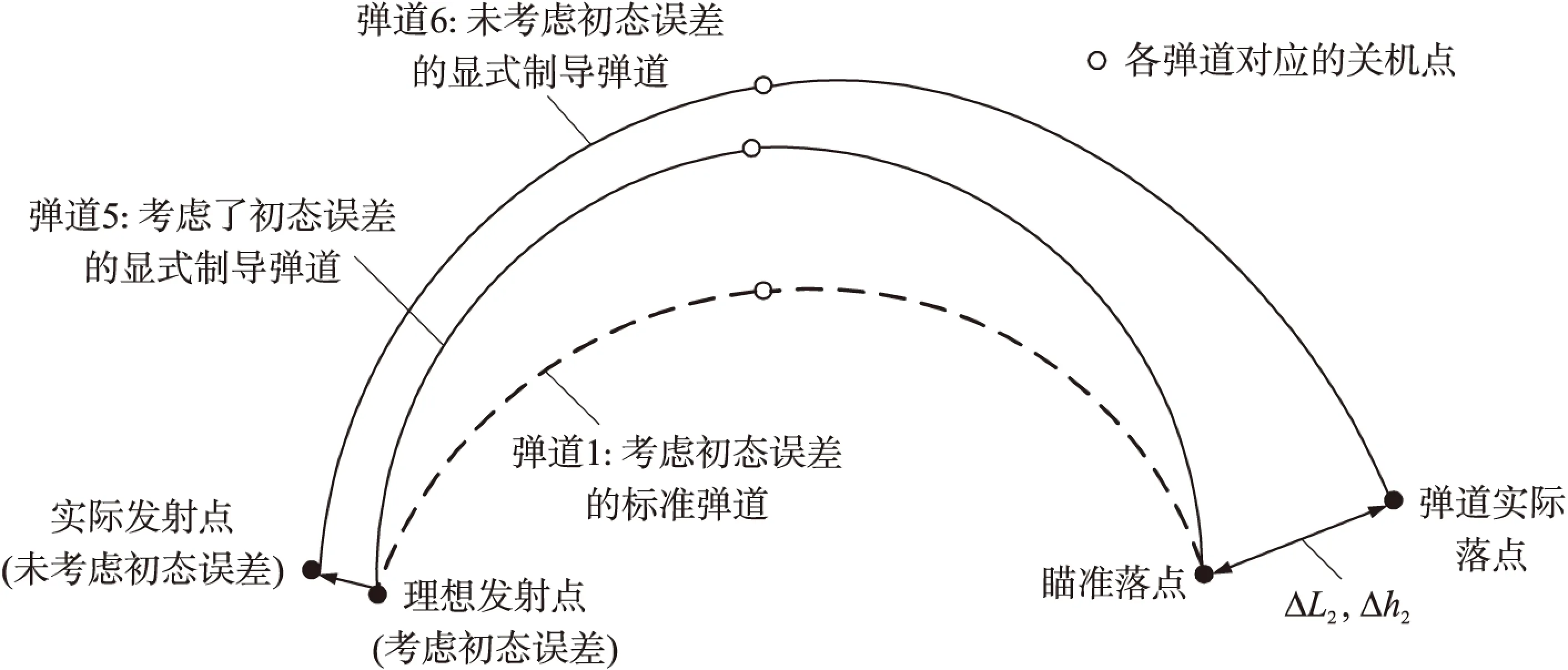
图2　初态误差对显式制导弹道的影响

3.1初态误差对导航计算的影响

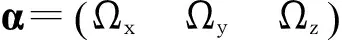
(1)

式中:E表示单位阵,

(2)

建立的导航误差方程为

(3)

式中:ΔgI是初态误差导致的引力误差;aP为视加速度。

式(3)中的导航误差又可分为以下4项:

①投影误差项。

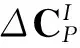
考虑初态误差时,地心坐标系(E系)与I系、P系之间的转换矩阵[1]分别为

(4)

(5)

(6)

式中:λT为天文经度,BT为天文纬度,AT为天文方位角,“Δ”表示对应参数的误差项;下标“T”表示天文坐标。

根据式(1)、式(6)推导可得:

(7)

由于许多情况下导弹发射前无法进行天文测量,这时可采用大地坐标代替天文坐标,大地坐标与天文坐标之间的关系[10]为

(8)

大地坐标误差与天文坐标误差之间也可通过垂线偏差计算误差Δξ,Δη进行换算[10]:

(9)

令初态误差K为

K=(ΔξΔηΔA0Δλ0ΔB0Δh0)T

(10)

初态误差通过投影产生的导航误差为

(11)

式中:v*(t),r*(t)分别为t时刻标准弹道的速度、位置状态;O为零矩阵；N为投影影响矩阵,包含速度投影矩阵Np,v和位置投影矩阵Np,r下标p表示投影；N中各元素如下:

N11=vycosAT,

N12=-vxcosAT+vzsinAT,

N13=-vysinAT,

N21=vysinAT,

N22=-vxsinAT-vzcosAT,

N23=vycosAT,

N31=-vz,

N32=0,

N33=vx,

N41=rycosBTsinAT+rzsinBT,

N42=-rxcosBTsinAT-rzcosBTcosAT,

N43=-rxsinBT+rycosBTcosAT,

N51=rycosAT,

N52=-rxcosAT+rzsinAT,

N53=-rysinAT,

N62=0,

N63=0。

②初始位置误差项。

Nr,0K

(12)

式中:rE0为发射点的地心距。

③初始速度误差项。

假设不考虑导弹发射时载体相对于发射系的速度,则导弹相对发射惯性坐标系的初始速度为

v0=ωe×RI0

(13)

式中:ωe,RI0分别为地球自转角速度和发射惯性坐标系中发射点位置矢量。

对式(13)求偏导可得初始速度误差为[10]

将克隆得到的LhsorMYB12测序结果与已报道的29个R2R3-MYB基因的氨基酸序列进行比对，结果表明，LhsorMYB12与MYB基因家族G6组中调控花青素苷合成的基因聚为一簇(图5)，与MYB基因家族成员中调控类黄酮生物合成的G7组及细胞分化的G15组关系较远[19]，说明 LhsorMYB12 基因在百合的花青素苷合成中可能起重要作用。在G6组中，单子叶和双子叶植物分别聚为一簇，单子叶植物中LhsorMYB12与百合科植物郁金香(KF990612.1)相似度最高，亲缘关系较近。

Δv0=ωe×ΔRI0+Δωe×RI0

(14)

式中:ωe在I系中的投影[1]为

(15)

RI0与RE0之间的转换关系为

(16)

Δωe和ΔRI0可通过对式(15)、式(16)求导计算获得。

对式(14)整理后可得初态误差K对初始速度的影响模型:

Δv0=Nv,0K

(17)

式中:

(18)

④引力误差项。

由于正常引力加速度g可分解为

(19)

式中:gr,gω分别为引力加速度沿地心矢量和地球自转角速度方向的分量;ρ为当前时刻导弹在发射惯性坐标系中的位置矢量;RI0为发射惯性坐标系中发射点位置矢量;ωe为地球自转角速度矢量。

对式(19)求导可得:

(20)

式(20)中关于引力项的偏导数为

(21)

式(21)中关于引力项的偏导数为

(22)

式中:

(23)

由于RI0和ωe均为K的函数，整理式(20),式(21)，式(22)后可得:

(24)

初态误差通过引力项产生的导航误差为

(25)

式中:下标g表示引力项。

根据式(11)、式(12)、式(17)、式(25)可得初态误差对关机点状态误差的影响分析模型:

(26)

式中误差项对关机点状态的影响关系为

(27)

式中:Np,r,Np,v,Ng,r,Ng,v是时间t的函数。

3.2初态误差对需要速度的影响

需要速度计算实际上属于两点边值问题[9]。假设采用给定固定飞行时间方案,当已知目标点位置参数时,需要速度误差Δvr(t)仅是当前时刻导弹位置误差Δr(t)的函数:

(28)

根据前面提出的导航误差方程,当前时刻位置误差与初态误差又可建立关系式:

(29)

将式(29)代入式(28)可得初态误差对需要速度的影响分析模型:

(30)

3.3初态误差对关机时间的影响

速度增益制导方案的关机方程为

vg=vr-v

(31)

该方案中增益速度vg为零时导弹关机,由此可见导弹关机时间是由需要速度vr和导航速度v共同决定的。

根据式(27)、式(30)和式(31)推导可知,当前时刻增益速度误差Δvg(t)为

(32)

由于|Δvg|→0时关机,显然初态误差是通过导航和需要速度计算误差对导弹的导引产生影响,进而使关机信号出现了误差并最终导致落点偏差。

4　仿真分析

4.1初态误差影响的分析方法

1)初态误差对弹道影响的分析方法。

(33)

2)初态误差对显式制导影响的分析方法。

在考虑初态误差与否的情况下，分别计算对应的显式制导弹道，对比其关机时间及对应的落点偏差ΔL2，Δh2。

初态误差对显式制导弹道和对标准弹道的影响结果误差量ΔL,Δh计算式为

(34)

4.2不同地区同射向发射的影响结果

假设初态误差如表1设置。

针对10 000km射程的某弹道,分别选取不同地形地区(海拔、地势相差较大)的3个发射点按0°发射方位角发射。初态误差对关机时间的影响结果如表2所示。

不同发射点区域初态误差对不同弹道命中精度的影响结果如表3所示。

根据表3中的结果计算的误差量ΔL,Δh如表4所示。

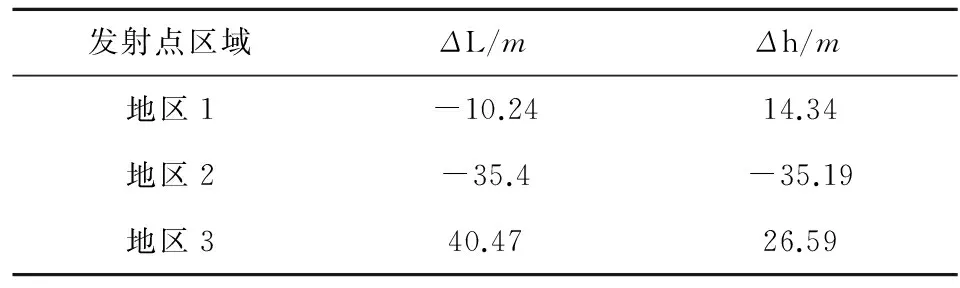
表4　不同发射地区初态误差对2种弹道

根据表3和表4的仿真结果,初态误差对不同发射点相同射向的显式制导弹道影响结果基本一致,偏差不超过5%。

4.3相同地区不同射向发射的影响结果

假设仿真初始条件与4.2节保持不变,在地区1发射点不同射向0°，30°，60°发射,初态误差对关机时间的影响如表5所示。

表5　不同发射方位角时初态误差对关机时间的影响

不同发射方位角初态误差对不同弹道命中精度的影响结果如表6所示。

表6　不同发射方位角时初态误差对命中精度的影响结果

根据表6中的结果计算的误差量ΔL,Δh如表7所示。

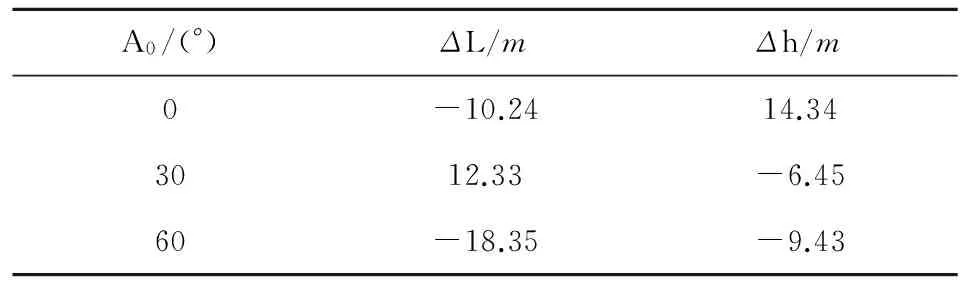
表7　不同发射方位角初态误差对2种弹道

根据表6和表7的仿真结果,同一地区不同射向情况下初态误差对标准弹道和显式制导弹道的影响结果偏差量在5%以内。

5　结论

①系统分析了初态误差对标准弹道、实际飞行弹道和显式制导弹道的影响机理,对分析初态误差的影响特性、提高弹道导弹的命中精度具有较好的参考价值。

②在整理、推导初态误差对导航计算的影响模型的基础上,给出了初态误差对需要速度计算的影响分析模型,并分析了初态误差对关机时间的影响机理。研究表明,初态误差对显式制导弹道的影响主要是因为导航误差的作用使得制导计算出现误差进而影响导弹的导引和关机控制,并最终导致落点偏差。

③仿真结果表明,不同发射地区同一射向条件下和相同发射地区不同射向条件下,初态误差对标准弹道、显式制导弹道的影响结果基本一致,误差在5%以内。

[1]郑伟,汤国建.扰动引力场中弹道导弹飞行力学[M].北京:国防工业出版社,2009.

ZHENG Wei,TANG Guo-jian.Flight dynamics of ballistic missile in gravity anomaly field[M].Beijing:National Defense Industry Press,2009.(in Chinese)

[2]张皞.快速逼近扰动引力的算法研究[D].郑州:信息工程大学,2007.

ZHANG Hao.A study on fast computation of trajectory disturbing gravity[D].Zhengzhou:Information Engineering University,2007.(in Chinese)

[3]李晓燕.扰动引力对弹道导弹落点影响分析[D].郑州:信息工程大学,2008.

LI Xiao-yan.Effects of disturbing gravity on the fall-point of trajectory missile[D].Zhengzhou:Information Engineering University,2008.(in Chinese)

[4]王明海,杨辉耀,何浩东.垂线偏差对导弹命中精度影响研究[J].飞行力学,1995,13(2):90-95.

WANG Ming-hai,YANG Hui-yao,HE Hao-dong.Research on the effect of the plumb-line deflexion for misile impact accuracy[J].Flight Dynamics,1995,13(2):90-95.(in Chinese)

[5]牟志华,阎肖鹏,赵丽莉.原点垂线偏差对远程导弹定位结果的影响[J].弹箭与制导学报,2007,27(3):176-178.

MU Zhi-hua,YAN Xiao-peng,ZHAO Li-li.The influence of plumb line deviation of launch point to long-distance missile’s orientation[J].Journal of Projectiles,Rocket,Missiles and Guidance,2007,27(3):176-178.(in Chinese)

[6]郑应强,康宁民,冯伟利,等.垂线偏差对惯性制导初始方位角的影响[J].中国惯性技术学报,2010,18(2):170-174.

ZHENG Ying-qiang,KANG Ning-min,FENG Wei-li,et al.Effect of vertical deflection on inertial guidance azimuth[J].Journal of Chinese Inertial Technology,2010,18(2):170-174.(in Chinese)

[7]贾沛然.垂线偏差对弹道导弹命中精度的影响[J].国防科技大学学报,1982(1):39-54.

JIA Pei-ran.The effect of deflection of the vertical on ballistic missile impact accuracy[J].Journal of National University of Defense Technology,1982(1):39-54.(in Chinese)

[8]张金槐.远程火箭精度分析与评估[M].长沙:国防科技大学出版社,1994.

ZHANG Jin-huai.Accuracy analysis and assess of launch vehicle[M].Changsha:National University of Defense Technology Press,1994.(in Chinese)

[9]鲜勇,李刚,苏娟,等.导弹制导理论与技术[M].北京:国防工业出版社,2015.

XIAN Yong,LI Gang,SU Juan,et al.Missile guidance theory and technology[M].Beijing:National Defense Industry Press,2015.(in Chinese)

[10]郑伟.地球物理摄动因素对远程弹道导弹命中精度的影响分析及补偿方法研究[D].长沙:国防科学技术大学,2006.

ZHENG Wei.Research on effect of geophysical disturbance factors and the compensation method for hit accuracy of long-range ballistic missile[D].Changsha:National University of Defense Technology,2006.(in Chinese)

Influence of Initial State Error on Hit Accuracy of Explicit Guidance Ballistic Missile

MA Bao-lin,ZHANG Hong-bo,WU Jie

(College of Aerospace Science and Engineering,National University of Defense Technology,Changsha 410073,China)

In order to analyze the influence of initial state error on the explicit guidance trajectory,the mechanism of initial error affecting the standard trajectory,actual flight trajectory and explicit guidance trajectory was analyzed.The analytical model of initial state error affecting guidance and required velocity was induced and deduced.Based on the model,the mechanism of initial error affecting explicit-guidance cut-off time was analyzed.The analytical method of initial state error affecting trajectory and explicit-guidance was proposed.The effect of initial state error on syntropy launching in different regions and different-direction launching in same region was simulated respectively.The simulation results show that the hit error of the standard trajectory and explicit guidance trajectory caused by initial state error is less than 5% without considering other navigation errors.

ballistic missile;earth disturbance gravity field;initial state error;explicit guidance;required velocity

2016-03-14

国家部委基金项目

马宝林(1983- ),男,博士研究生,研究方向为导航、制导与控制。E-mail:feizhuxiongmao@126.com。

V412.2

A

1004-499X(2016)03-0023-07