经历操作过程建构数学模型

刘雪梅

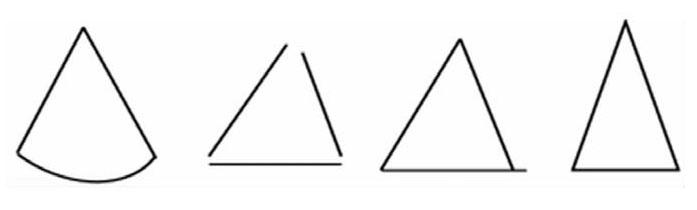
“三角形的三边关系”是在学生初步了解三角形一些基本特征的基础上学习的，学生虽然知道了三角形有三条边，但对三角形“边”的研究却是首次接触，短短的四十分钟之内要让学生从抽象的几何图形中发现三角形三边的关系，并加以应用并非那么容易。备课时，我一直在思考：如何让学生既学到知识又能渗透数学模型思想？为实现这一目标，我采取了“一明一暗”两条线协同并进的教学思路。既让学生在经历观察、猜想、验证、归纳等数学活动中归纳得出“三角形任意两边之和大于第三边”这一结论；同时又让学生经历“发现问题——大胆猜测——多种方法验证——归纳得出结论——灵活应用”这一数学乃至科学研究的一般方法和过程，让学生在学到知识的同时，逐步渗透数学建模思想。

一、提出问题，初步探模

1.案例描述：谈话交流，引入新课

师：孩子们，我们已经初步认识了三角形，谁能说说三角形有什么特征？

生：三角形有3个角、3条边、3个顶点。

师：说得真好！还有谁要补充？

生：三角形是由三条线段首尾相接的图形。

师：是不是，同学们？

生：是！

师：那下面的图形哪个是三角形呢？

生：（举手）第4个。

师：那第1个为什么不是？

生：因为它下面那条线是弯曲的。

师：是的，三角形的三条边都是直的。那第二个为什么不是呢？

生：因为它的三条边没有首尾相接。

师：不错！第三个呢？

生：因为有一条线段多出来一点了。

师：（机智地牵引）也就是说，我们没有充分利用这三条线段的长度，是吗？

生：是！

过渡：如果老师也给你提供这样的3条线段，你能围一个三角形吗？

生：能！

2.案例思考

教师通过回顾旧知，进一步使学生明确三角形的基本特征，尤其“三角形是三条边首尾相接围成的封闭图形”这一要点，为学生接下来的“围一围”操作活动以及“什么样的三条线段才能围成一个三角形？”的活动猜想提供了一定的依据。最后创设了“给你提供3条线段，你能围一个三角形吗？”这样的问题情境，为学生自主学习搭建一个平台，让学生在老师略带“挑衅”的激励下积极主动地参与学习研究，在更自由、更广阔的空间中去合作、探索和发现。

二、操作质疑，探究新模

1.案例描述：动手操作，引发冲突

生：（动手围三角形）

师：（激励）嗯，真不错，有的孩子动作很快！（边巡视边指导）

师：你们太棒了，这么短的时间就围成啦？唉？好像还有同学没围成嘛？这样吧，小组同学帮帮他，看他怎么回事，怎么没围成呢？

生：（小组里积极互助）（有人举手求助）老师，他这个围不成！

师：（参与到小组中看看）

生：（围不成的学生举手）

师：怎么了？还围不成啊！这样吧，让刘老师来试试？（将一学生的纸条放上展示

台：3cm、5cm 、10cm）围成了吗？

生：没有！

师：嗯，是围不成嘛！什么原因呢？

生：（指展示台）因为这两条太短了！它们接不起来。

师：是吗？你关注了线段的长度，真不错！那么怎样才能让它们接起来呢？

生：把下面这个根10cm的换短一些。

师：不错。如果下面的这根长度不变，还有别的办法吗？

生：可以把上面两根加长。

师：唉，可以吗？我们来试试。（把3cm、5 cm换成4cm、6cm）

2.案例描述：互动思考，引发猜想

师：（边操作边叙述）想象一下，如果我让4cm和6cm这两条线段往下压，会和10 cm的线段围成三角形吗？

生1：它们会成一条直线。

生2：它们会合在一起。

师：也就是说，三个顶点会在一条-----直线上！真的会是这样吗？想不想看一下？来，我们一起看。（师演示4cm和6cm两条线段往下压，先压一段）这是三角形吗？（师演示4cm和6cm继续往下压，直到接上）接是接上了，是三角形吗？

生：不是！

师：还没围成，那怎么办？

生：把4cm和6cm再加长！

师：再加长，一定能围成三角形吗？

生：行，只要让上面两条线段加起来大于下面那条线段就可以了！

师：嗯，有想法！到底行不行呢，我们用事实说话，一起来看大屏幕。（师演示围5cm、7cm 、10cm）成了吗？

生：成了！

师：（同时出示三组实验数据）同学们，通过刚才的实验操作，我们一起来回顾一

下：三条线段要想围成三角形，看来跟线段的什么有关呢？需要符合什么样的条件啊？

生：我觉得三条线段要想围成三角形跟线段的长度有关，要让上面两条线段加起来的和大于下面那条最长线段，才可以围成三角形。

师：同学们，你们同意吗？

生：同意！

师：准确地说，就是（边说边贴黑板贴：两条较短线段的长度和大于最长线段能围成三角形）那它们的和要等于最长线段呢？小于呢？（板书：等于小于不能围成三角形）

师：这就是我们共同研究的初步发现。那么，对于这个发现，同学们有疑问吗？（预设：①有，……；好！等会儿我们来一一验证！②没有；那么到底对不对呢，还需要我们去验证）

3.案例思考

学生在自主探究中发现：有的同学用三条线段能围成三角形，有的则围不成三角形，事实推翻了学生头脑中以前的错误认知，激起了思维的矛盾，使学生不得不重新认识三角形三边之间的关系。这种重新认识是学生对三角形三边关系认识上的第一层次。教师抓住这一契机巧妙设疑：为什么有的三条线段不能围成一个三角形？怎样的三条线段才能够围成一个三角形呢？学生经历摆的过程直观地发现：两条较短线段长度之和小于或等于最长线段时，不能围成三角形，只有大于最长线段时，才能围成三角形，得出了三角形两条短边之和大于最长边的结论。至此，学生初步认识了三角形三边的关系。这种初步认识是学生对三角形三边关系的第一次建模，也是认识上的第二层次，是学生思维发展必然经历的一个阶段。

三、实验验证，深入建模

1.案例描述

师：刚才，你们也围成了一些三角形，看看，是不是两条较短线段的长度和大于最长线段，互相说一说！（教师巡视）

师：来！先请你说你这个三角形较短线段是几厘米和几厘米？

生1：（6cm、7cm 、9cm）较短线段是6cm和7cm，6+7>9，所以能围成三角形。

师：说的真完整！再请一位同学来说。（请三位同学分别说）

师：（3cm、7cm 、7cm）你们有疑问吗？

生：没有！

师：它哪有两条较短线段呀？它不就只有一个3cm最短吗？

生：它两条较长的线段都是7cm，所以只要任选其中一条和最短的线段3cm加起来就可以了。

师：（找到一个等边三角形：5cm、5cm 、5cm）那这个三角形，它哪来的较短线段？

哪来的最长线段呀？

生：就是随便哪两个5cm加起来都大于另一个5cm，所以都能围成三角形。

师：所以，任选两条线段加起来的和都大于另一条线段，是吗？但是我们在围三角形的时候还有这样一种三角形，它三条线段长度各不相同，那你说，它任意两条线段的和都大于第三条线段吗？（设问、验证）

生（大胆猜测）：是的，任意两条线段的和都大于第三条线段，不然就围不成三角形了。

师：比如说------

生：比如说最短的两条加起来一定大于最长的那条。

师：那如果我把这样的三角形三条边给它标上号，分别是，那么+和什么关系？

生：+肯定是大于的，否则它就围不成三角形了。

师：（PPT出示+>）那+呢？

生：+肯定是大于的，最长的一条线段跟最短的一条线段相加，最长的线段本来就大于了，再加上肯定比大了。

师：哦，太好了，不但会思考而且会推理，真棒！再来看，+和比呢？

生：+肯定大于，因为和都比大，它们加起来一定比大。

师：所以，对于这样的三角形，它也是任意两条线段的和大于第三条线段。

师：在三角形中，我们可以把围成三角形的这三条线段叫做三角形的边（PPT出示：边）那么，同学们，你们又有什么新的发现了吗？

生：三角形任意两边长度的和大于第三边。（PPT出示）（揭示板书及课题）

2.案例思考

数学模型的形成是一个逐步抽象的过程，怎样抽象和建构数学模型呢？学生通过大量的操作感悟和理性分析，已经积累了一定的数学活动经验。原本以为“三角形两条短边之和大于最长边”的结论会得到教师的肯定，然而，教师的反应仅仅是“是吗？”二字，这使学生敏感地意识到这种表达可能有问题，问题出在哪呢？学生不得不深思。教师适时引出两组数据（3cm、7cm 、7cm；5cm、5cm 、5cm），也就是当没有两条较短线段，也没有最长线段的时候如何检验学生先前得出的结论呢？最后学生终于发现：在三角形中，任意两边之和都大于第三边。对“任意”二字的理解，使学生对三角形三边之间关系的认识得到了深化。这种深化的认识和理解是学生对三角形三边关系的再次建模，是认识上的第三层次。最后，教师引入用字母式子表示，体现了规律的简洁性。至此，学生对数学模型完成了建构，理解也更加深刻。