“问题导学”下的高三数学复习课有效性研究——《椭圆的定义及其标准方程》同课异构课例点评

□广东省广州市增城中学　李宇宇

“问题导学”下的高三数学复习课有效性研究
——《椭圆的定义及其标准方程》同课异构课例点评

□广东省广州市增城中学李宇宇

“问题导学”模式的显著特点是为学生提供广阔的思考空间，思维活动的自由度较大，学生的思维活动易于展开，在思考中能提出更多的问题，解决问题的途径也更多。下面结合两节同课异构课谈谈目前高三数学复习课中的推进情况及复习策略的研究。

［策略一］“目标定位”首当其冲

数学课堂教学中课堂目标定位问题不但关系到教学任务能否顺利完成，更关系到一堂课的教学成效，所以对目标定位问题的分析至关重要。

在《椭圆及其标准方程》的课例中，第一位老师的目标定位在学会如何运用椭圆的定义解决相关问题，学生会求椭圆的标准方程。第二位老师将目标定位在通过模型的讲授方式，学生进行自我建构，领悟椭圆研究的方法。显然定位不同，所选择的讲解方向和例题习题都有较大的区别。

师2：利用五个问题进行讲解和师生合作、小组合作，主目的是想学生建构椭圆的几类题型的方向。设计如下——

问题1：什么叫作曲线的方程？求曲线方程的一般步骤是什么？其中哪几个步骤必不可少？

问题2：椭圆的定义是什么？

问题3：如何推导出椭圆的方程？

问题4：有哪些性质？怎么观察得到？按什么方式去深入了解椭圆模型？

问题5：椭圆模型能解决关于椭圆方向上的什么问题？

因此，教师在进行教学设计时，要充分考虑学生学情，精选例题与习题。在小结时，要站在一个数学思想方法的高度上审视学生的思维，对所有方法进行思维暴露及方法提炼。

［策略二］舍得“放纵”学生

师1在讲解例题3时，让学生通过小组合作解决问题，并请学生代表发言。由于时间紧迫，教师立刻引导学生讲出几种不同的思路，给予学生的时间不足。师2在讲解例题时让学生将解答过程写在白板上（每个小组配备一块），然后再请小组代表进行展示，既很好地实施了"问题导学"课堂的小组合作学习，又给予学生展示的时间和空间，效果较好。

师2在讲课过程中对“舍得”把握得比较到位，成为了这节课最大的亮点。从他们的两节课中，我作出反思是：

1.让“问题导学”课堂轻松而不随意。先来看看这个问题：“老师讲题与老师做题的区别是什么？”直接把正确答案讲给学生听，就是老师在黑板上做题，而讲题的过程应该是顺着学生的思维去引导和修正。

比如，例题3（2013全国大纲文T8）：“已知F1（-1，0），F2（1，0）是椭圆C的两个交点，过F2且垂直于x轴的直线交椭圆c于A、B两点，且|AB|=3，求椭圆C的方程。”师1在处理该例题时，教学设计的思路是让学生充分展开，并进行一题多解，但是当学生给出两种方法后，老师为了完成教学任务，用自己认为的“导”轻松帮学生完成了另外三种解法。“问题导学”课堂倡导的是最大限度地发挥学生的主观能动性。

且看笔者在一节高三复习课《基本不等式》上与文科班的学生如何共同探讨此题吧。题目：“已知a＞0，b＞0，A（1，1），B（a，0），C（0，b）三点共线，求a+b的最小值”，教师可能会利用课堂快速处理，稍微讲讲思路，用两种左右的方法达到讲课的目的。然而，当笔者真正“舍得”给予学生足够的思维空间时，我们有了以下几种精彩的解答：

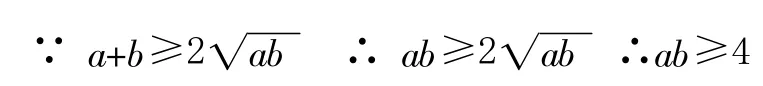
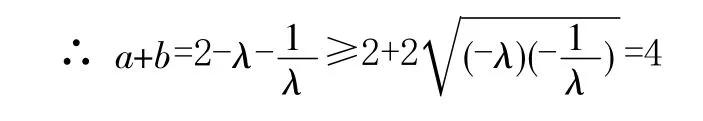
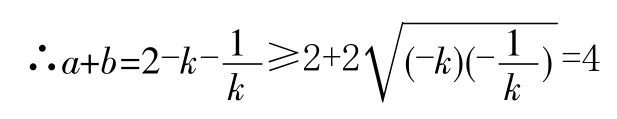
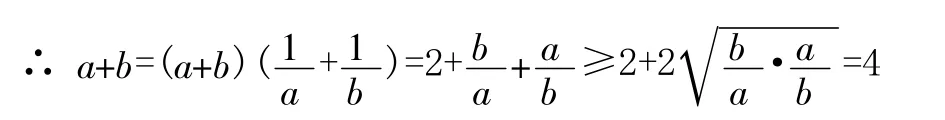
五种不同的解法全部是经过学生小组合作学习充分酝酿的成果，这也是笔者在课前没有想到的。如果学生的思维得到开发，那他们离成功就不远了。这个过程中学生思维火花的碰撞和感悟，“基本不等式”在求最值中的灵活运用给学生留下了深刻的印象。当然，教师还可以在此基础上提出问题，或鼓励学生提出问题，搜查在解答过程中存在的不足。

2.让学生变被动为主动，学会学习。当遇到陌生的题目时，首先应该进行回顾。比如，以前遇到过类似的问题吗？以前是用什么方法解决的？正确审题是解决数学问题的前提和保证，审题包括对所研究问题有一个全面的了解，包括所涉及的知识点以及可能用到的方式方法，了解整个问题的前因后果，要清楚地知道每个条件之间的关系，理解它们的知识体系。

3.让学生学会推而广之。推广是事物发展所遵循的规律之一。当我们从研究一个对象过渡到研究包含该对象的一个集合，或从研究一个较小的集合过渡到研究一个包含该集合的一个更大的集合时，就是推广，反之就是收缩。

在立体几何中，学生的很多空间概念和性质都是建立在对平面几何的认识之上的。如“平行公理”、“勾股定理”等。但是，已有的知识有时也会产生负迁移，如“平面内到定点的距离等于定长的点的轨迹是圆”，此命题推广到空间则不成立。教师需特别强调：将平面几何的结论向空间进行推广时，必须遵循“言必有据”的原则，绝不能养成学生随心所欲的习惯。

［策略三］“导”的智慧

高三复习是学生站在高中数学整体高度上的“二次学习”，学生已具有较丰富的数学知识，具备一定的数学能力，更加有利于在教师的引导下广泛地探究问题，从而可以让学生更加深入地理解数学概念，进一步提高其数学能力。

如何对学生的主体学习实施科学引导和有效指导？笔者认为，在思维受阻时指导，“导”重在关键知识点上的指导和方法技能上的指导，而且必须是适时的、富于启发性的“导”。在《椭圆的定义及其标准方程》课例中，由学生完成题目的求解过程，两位老师均能引导学生对此类题型进行反思与回顾，提炼方法，探寻规律.让学生思维能力得以提升，探寻问题解决的一般方法，这是高三复习中“导”的关键。实践让笔者感悟到，在高三复习课堂上数学教师要善于将本质的数学思想内容巧设成一系列问题，以此引领使学生“想学”、“会学”、“主动学”，有效地提高课堂复习的效益。

高三数学复习课，教师要避免知识的简单“重复”，将“问题导学”教学模式切实落实到自己的复习课中，用“舍得”的心态提高教与学的效率。“问题导学”教学模式正是将高三数学老师从课堂教学模式单一枯燥的困局中很好地解救了出来，通过学生的小组合作学习探究，学生大面积参与其中，课堂氛围有了很大的转变。

广州市教育科研协作基地资助项目“课堂教学改革科研基地”（编号：14XZ19）；广州市教育科学“十二五”规划课题“高中‘问题导学’课堂教学模式研究”（课题批准号：2013B460））