运用分类讨论思想,提高高一新生“四种能力”
□海南省海口市琼山中学陈运富
运用分类讨论思想,提高高一新生“四种能力”
□海南省海口市琼山中学陈运富
初中生刚进入高中大都有一个普遍的体会:高中数学好难学。根本原因在于初中数学课程对学生的抽象思维能力、逻辑推理与判断能力、空间想象能力、数学运算能力要求不高,与高中数学相比存在着很大的差异。高中必须掌握的某些数学知识和思想在初中阶段老师都没有讲授或者是没有重点强调,使得学生在初中阶段所掌握的数学基础知识、基本技能和数学能力有时候没法适应高中数学的学习要求。下面我主要是浅谈高一教学中必须给学生过渡的重要思想之一:分类讨论的思想方法。
分类讨论是指在解决一个复杂问题时,应将讨论的对象分成若干相对简单的情况,然后对各种情况逐个讨论,最终使整个问题得以解决。分类的一般原则是不重不漏,特别是不能遗漏所讨论问题的各种情形。要让学生认识到分类讨论主要是“化整为零,各个击破,再积零为整”的数学策略。因此,在讲授的过程中,一定要让学生明白“为什么要分”,“要分谁”,“怎么分”。在日常生活中,我们常常会用到它,在数学的学习过程中它也是必不可缺的基本思想方法。初中的教学就应该时常渗透这种思想方法,如,在讲绝对值、方程、函数、不等式等内容时,都可以编写一些题目让学生进行分类讨论。分类讨论既能训练人的思维条理性和严密性,又能让学生在学习过程中感受到数学的逻辑美。下面就初中几个代数的教学案例,分析一下怎样渗入分类讨论的思想。
案例1:解不等式(k-1)x>k2-1。
分析:在不等式当中,我们一定要强调两边不能同时除以一个不确定的数,在这个不等式当中很多学生会不经意地就在不等式两边同时除以k-1来求解,因而会落掉一些解。因此,在讲解过程中教师应该要让学生明白为什么要分类讨论,是因为k-1的符号我们无法确定,它有可能出现正数,负数和零,因此,我们要对k-1进行分类讨论,因此分类如下——
解:当k-1>0时,即k>1时,则x>k+1;
当k-1=0时,即k=1时,原不等式为0·x>0,不等式无解;
当k-1<0时,即k<1时,则x<k+1。
综上所述:当k>1时,则x>k+1;当时,不等式无解;
当k<1时,则x<k+1。
案例2:解方程|4x-4|-|2x+2|=14
分析:解决有关绝对值的问题,一定要让学生知道关键是去掉绝对值,而要去掉绝对值就必须知道绝对值下的数的符号,所以根据原方程中绝对值下的数可能出现的情况(两个绝对值下的式子同为正,两个同为负,两个一正一负)给它进行分类讨论,再逐个击破,解法如下:
解:(1)当x≥1时,原方程化为(4x-4)-(2x+2)=14,x=10。
当-1≤x≤1时,原方程化为(4x-4)-(2x+2)=14,x=-2,不合题意,舍去。
当x≤-1时,原方程化为(4x-4)-(2x+2)=14,x=-4。
∴综述,x=10或-4。
案例3:设f(x)=x2-2x-1在区间[t,t+1]上的最小值是g(t),求g(t)。
分析:二次函数f(x)=x2-2x-1=(x-1)2-2,当x=1时取得最小值-2,在区间[t,t+1]中,t具体的值我们无法确定,所以x=1是否在区间[t,t+1]内我们得进行分类讨论,大体上就分为在区间[t,t+1]内和不在区间[t,t+1]内(不在又分为在区间左边和右边),因此我们就此题分类讨论如下:
解:f(x)=x2-2x-1=(x-1)2-2,当x=1时取得最小值-2
当1∈[t,t+1]时,即0≤t≤1,g(t)=-2;
当t>1时,g(t)=f(t)=t2-t-1;
当t+1<1时,即t<0时,g(t)=f(t+1)=t2-2,
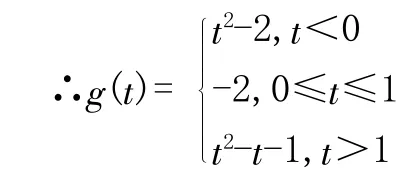
说明:对于含参二次函数求最值的问题,解决此类问题的基本思路为:根据二次函数的对称轴相对定义域区间的位置进行分类,再利用分类讨论思想方法进行求解。
数学教学是进一步以构建科学合理的教学思维体系,强化培养学生规范、合理、严谨的学习品质为目的改进,初中的一些数学思想方法的渗入能促进学生更快地适应高中数学学习。

