具有多面体不确定和有界扰动的异构混沌系统同步控制

张智群，孙学耕，尚伟科

(1.福建信息职业技术学院电子工程系，福州 350003；2.中国电子科技集团公司第38研究所预警探测研发中心，合肥230088)



具有多面体不确定和有界扰动的异构混沌系统同步控制

张智群1，孙学耕1，尚伟科2

(1.福建信息职业技术学院电子工程系，福州 350003；2.中国电子科技集团公司第38研究所预警探测研发中心，合肥230088)

针对一类具有时变多面体不确定和有界扰动的异构混沌系统，研究了其自适应同步控制问题。针对主从系统的异构特性，采用辅助系统的方法，分别给出了主从混沌系统广义同步的连续时间控制律和非连续时间控制律。作为一个特例，还给出了主从系统完全同步的充分条件。最后，通过数值仿真验证了结果的有效性。

多面体不确定；异构混沌系统；自适应控制同步

0　前言

自从混沌现象在物理学中被发现以来，混沌系统得到了广泛的关注。而混沌同步在诸如信息科学、医学、生物工程等各个领域具有其独特的实用价值。混沌系统的同步控制问题在1990年首次得到研究[1]，自那以后便有大量的同步方法不断被报道[2-6]。

混沌系统同步问题根据系统耦合配置的不同可以分为两种情况[7]：自同步和主从同步。其中，混沌系统主从同步问题由于其在保密通信中的显著应用价值，在过去20多年得到了相当多的关注[2，7-12]。因此，大量的主从同步控制方法被提出，包括反步设计、脉冲控制、不变流形方法、自适应控制、滑模控制等等[4-5，13-21]。大多数已有工作都是考虑主从混沌系统具有相同系统结构并且系统参数精确可知的情况，然而在实际系统中，有些参数在先前往往并非精确可知，信息传输过程中的外部扰动也是不可避免的。参数不确定在实际中很容易引起系统震荡、不稳定或者导致系统性能变坏，多面体不确定被广泛地用来描述各类系统中的参数不确定[22-24]。例如，用电路搭建的混沌系统，其中电阻等参数随着外部环境的变化便可以尝试用时变多面体不确定来描述。由于时变多面体不确定可能会破坏混沌系统在理想条件下的同步，针对具有时变多面体不确定的异构混沌系统的控制同步问题目前还有待进一步研究。另一方面，广义同步概念包含多种不同的同步形式，例如，反同步、延迟同步、投影同步、全状态混合投影同步，等等，因此，研究主从混沌系统的广义同步更具有实用价值。受以上这些因素启发，本文研究具有时变多面体不确定和外部扰动的异构混沌系统的自适应广义同步控制问题。

本文的其余部分将按如下组织展开。第1节将进行问题阐述，主要结论在第2节给出，然后在第3节用数值仿真来验证结论的有效性，第4节总结全文。

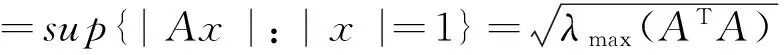
1　问题描述

考虑如下具有时变多面体不确定和有界噪声的主从混沌系统：

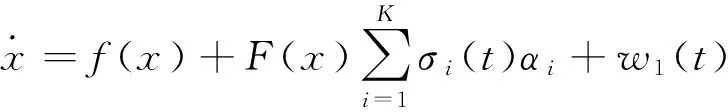
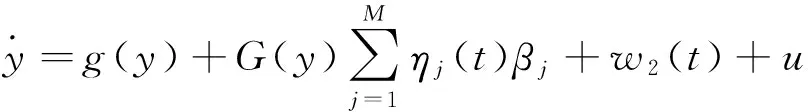
(1)

式中：x，y∈Rn为系统状态；u为从端系统的控制输入；f(·)，g(·)∈C1(Rn，Rn)和F(·)，G(·)∈C1(Rn，Rn×m)都为已知的连续时间非线性函数，分别表示与系统参数无耦合以及与参数有耦合的系统非线性特性；αi，βj∈Rm为已知的系统参数；σi(t)，ηj(t)表示未知的时变不确定性，且满足

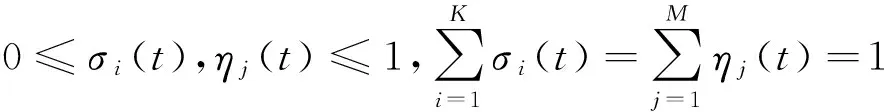
式中：K，M表示多面体的顶点数；w1(t)，w2(t)是系统所受到的有界扰动，且有|w1(t)|≤L1，|w2(t)|≤L2。

不失一般性，我们可以通过简单的分析和变换，将上述系统转换成如下具有统一不确定性形式的主从系统：

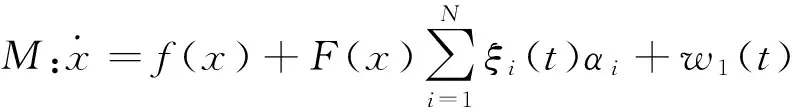
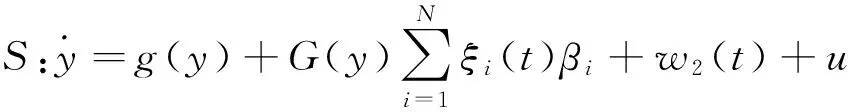
(2)

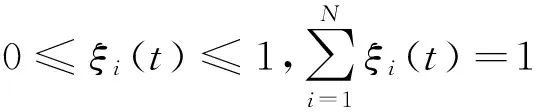
本文中将以系统(2)为研究对象，设计自适应控制器，使得主从混沌系统达到同步，并且设计自适应律来确定系统中的未知参数。使得主从混沌系统达到广义状态同步的控制目标，可以描述为：

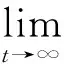
(3)

式中φ(·)：Rn→Rn表示同步映射。

如果主从混沌系统的状态满足上述表达式，即称主从混沌系统达到广义同步，作为一个特例，如果φ(x)=x则称为完全同步；如果φ(x)=-x则称为反同步。

对于异构主从混沌系统，直接设计控制器达到广义状态同步会比较困难。因此，我们考虑采用文献[10]和文献[14]中提出的辅助系统方法，所使用的辅助系统与主端系统具有相同的系统结构。

(4)

式中：θi(t)为待确定的时变参数变量；v为待设计的辅助系统虚拟控制量。

这里的想法是，我们构造一个上述的辅助系统，与驱动系统或者响应系统具有相同的系统结构，但不具有相同的初始条件。辅助系统是虚拟的，但更便于分析和设计。如果响应系统和辅助系统的同步流形达到稳定，则结果可以表明驱动系统和响应系统达到了广义同步。

为了后续分析过程的方便，我们给出如下著名的引理。

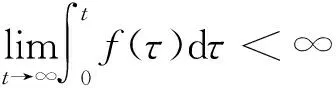
2　主要结果

在本节当中，我们将给出主从混沌系统(2)的自适应广义同步的充分条件，同时将分别给出连续时间形式和非连续时间形式的自适应控制律。

(5)

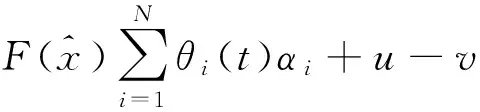
(6)

式中Dφ∈Rn×n是同步映射φ(x)的雅克比矩阵。

由于混沌系统状态的有界性，Dφ也是有界的。容易看出，如果e1→0，e2→0，则控制目标(3)将得到满足，即e→0。

2.1非连续自适应律

定理1如果下面条件满足，则具有时变多面体不确定和有界扰动的主从混沌系统(2)是广义状态同步的。

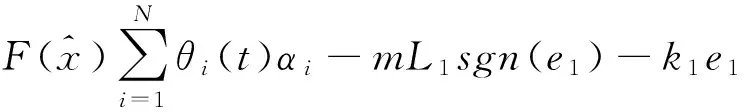
(7)

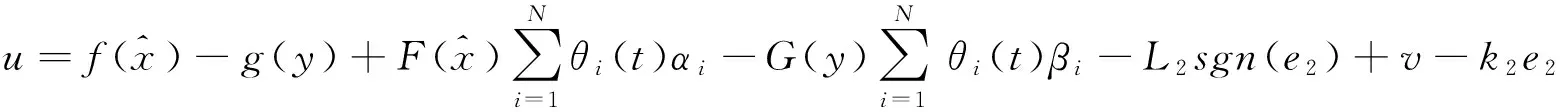
(8)

(9)

其中

(10)

且k1>0，k2>0 是用来调节收敛速率的正常数。

对上式两边求导数，则有

考虑到 |w1(t)|≤L1，|w2(t)|≤L2，因此有

代入前面不等式，有

土地是财富之母，是我国农村人口的重要财富来源与财富象征；同时，土地是重要的生产和生活资料。贵州省山多地少，可以利用的土地资源稀缺，因此，充分利用好土地资源，通过政策、工程手段、科学技术等发挥其潜在价值，对于贵州省实施精准扶贫，帮助农村地区贫困人口摆脱贫困，走可持续发展的致富之路具有重要的理论意义和现实价值。

代入自适应律(9)，且注意到 0≤ξi(t)，αi(t)≤1，我们有如下不等式：

其中V(0)是V(t)的初始值。因此e1，e2∈L2，因为V(0)是有限的。

根据引理Barbalat’s lemma，我们容易得到e1→0，e2→0，当t→∞，且‖e‖≤‖e1‖+‖e2‖→0。因此，误差动态系统是渐近稳定的，或者说具有时变多面体不确定和有界扰动的主从混沌系统(2)是渐近广义同步的。

2.2连续自适应律

一个非连续的自适应律在工程实现中可能会带来麻烦，比如频繁的切换，因此在下文我们将针对主从混沌系统的广义状态同步给出一个连续的自适应律。

定理2对于具有时变多面体不确定和有界扰动的异构混沌系统(2)，如果下述条件满足，则主从系统将达到同步控制目标(3)。

(11)

(12)

自适应律θi(t)将按下式更新

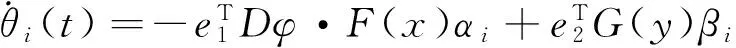
(13)

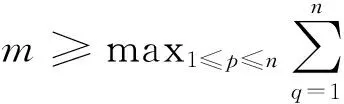
证明：选定如下Lyapunov函数

考虑|w1(t)|≤L1，|w2(t)|≤L2，因此

由式(13)，我们有

定理证毕。

2.3完全状态同步控制律设计

作为一个特例，我们将直接给出系统(2)完全状态同步的相关结果，证明过程将被省略。

推论1具有时变多面体不确定和有界扰动的异构混沌系统(2)将达到完全状态同步，如果满足如下条件：

(15)

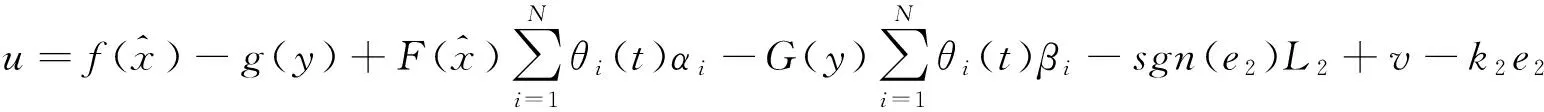
(16)

且θi(t)由下式决定

(17)

其中k1，k2是用来调节收敛速率的正常数。

推论2具有时变多面体不确定和有界扰动的异构混沌系统(2)将达到完全状态同步，如果满足如下条件：

(18)

(19)

且自适应律θi(t)按下式更新

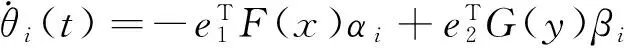
(20)

其中k1，k2是用来调节收敛速率的正常数。

3　数值仿真

本节我们将分别给出完全状态同步和投影同步的数值仿真算例来验证所提同步策略的有效性。为了不失一般性，推论1用来设计控制律使得异构的主从混沌系统达到完全状态同步；定理2用来设计自适应控制律达到广义状态同步。

考虑Lorenz系统和Chen系统

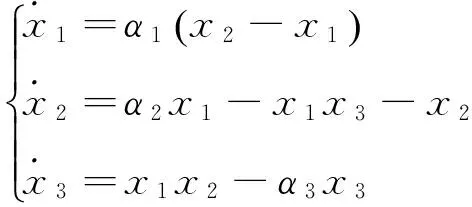
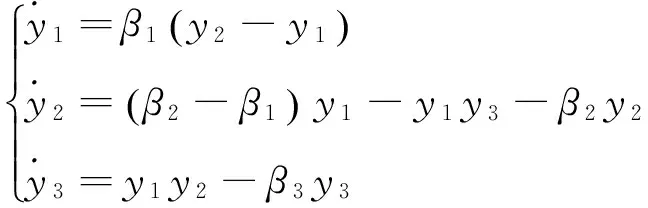
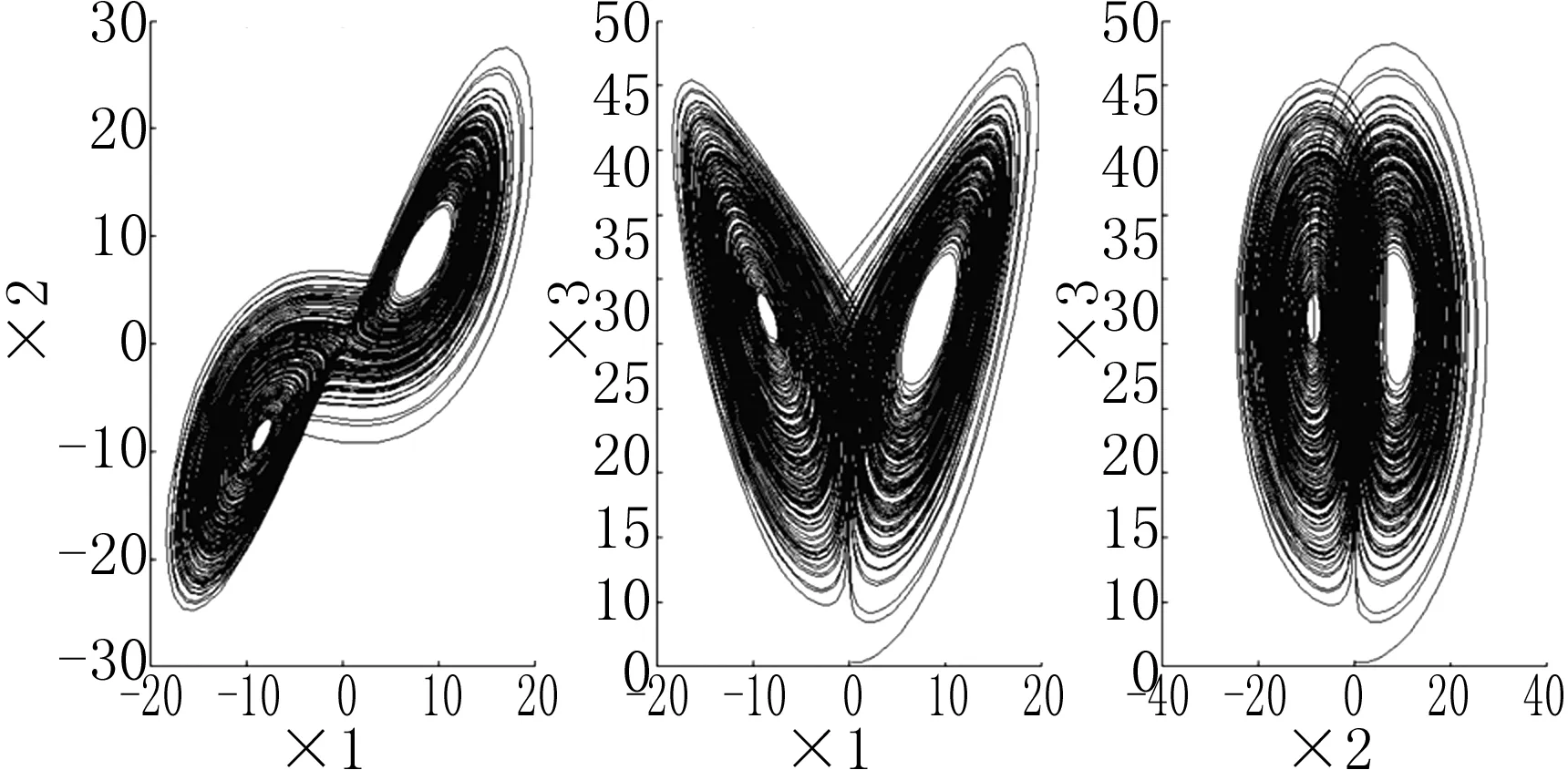
图1　Lorenz混沌系统的吸引子

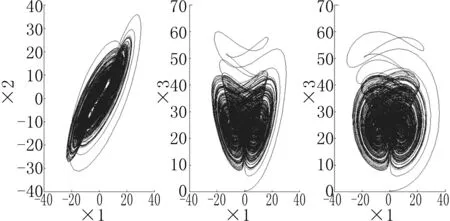
图2　Chen混沌系统的吸引子

考虑系统中的不确定参数和传输信道中的有界扰动，我们将主从系统按(2)的形式重写如下：

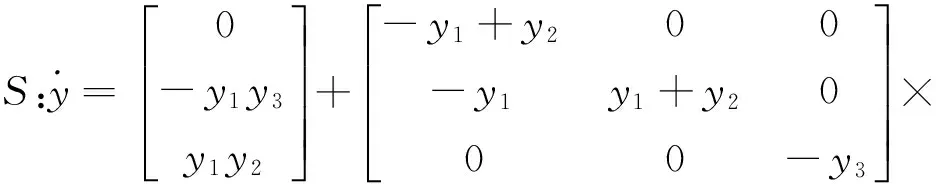
以及辅助系统

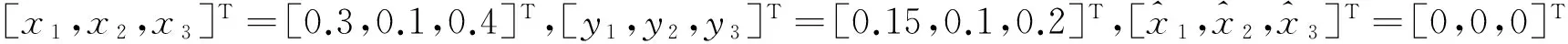
3.1完全状态同步

取k1=50，k2=50。数值仿真结果如图3～图5所示。误差曲线渐近收敛。

图和x之间的完全状态同步误差

图和y之间的完全状态同步误差

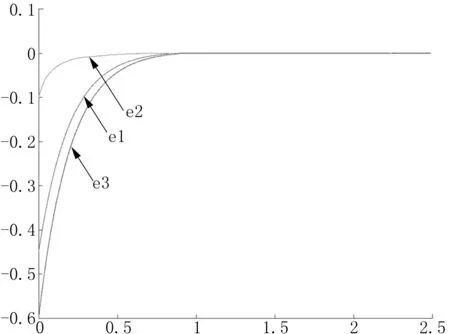
图5　y和x之间的完全状态同步误差

3.2广义同步

取k1=10，k2=10，m=80，且有φ(x)=(x1，-x2，x2x3)T，则

自适应律θi(t)按下式更新

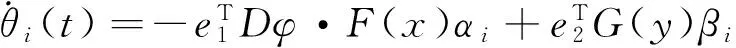
其中初始值取θ1(0)=0.3，θ2(0)=0.7。数值仿真结果如图6～8所示，结果表明所提同步方法是有效的。

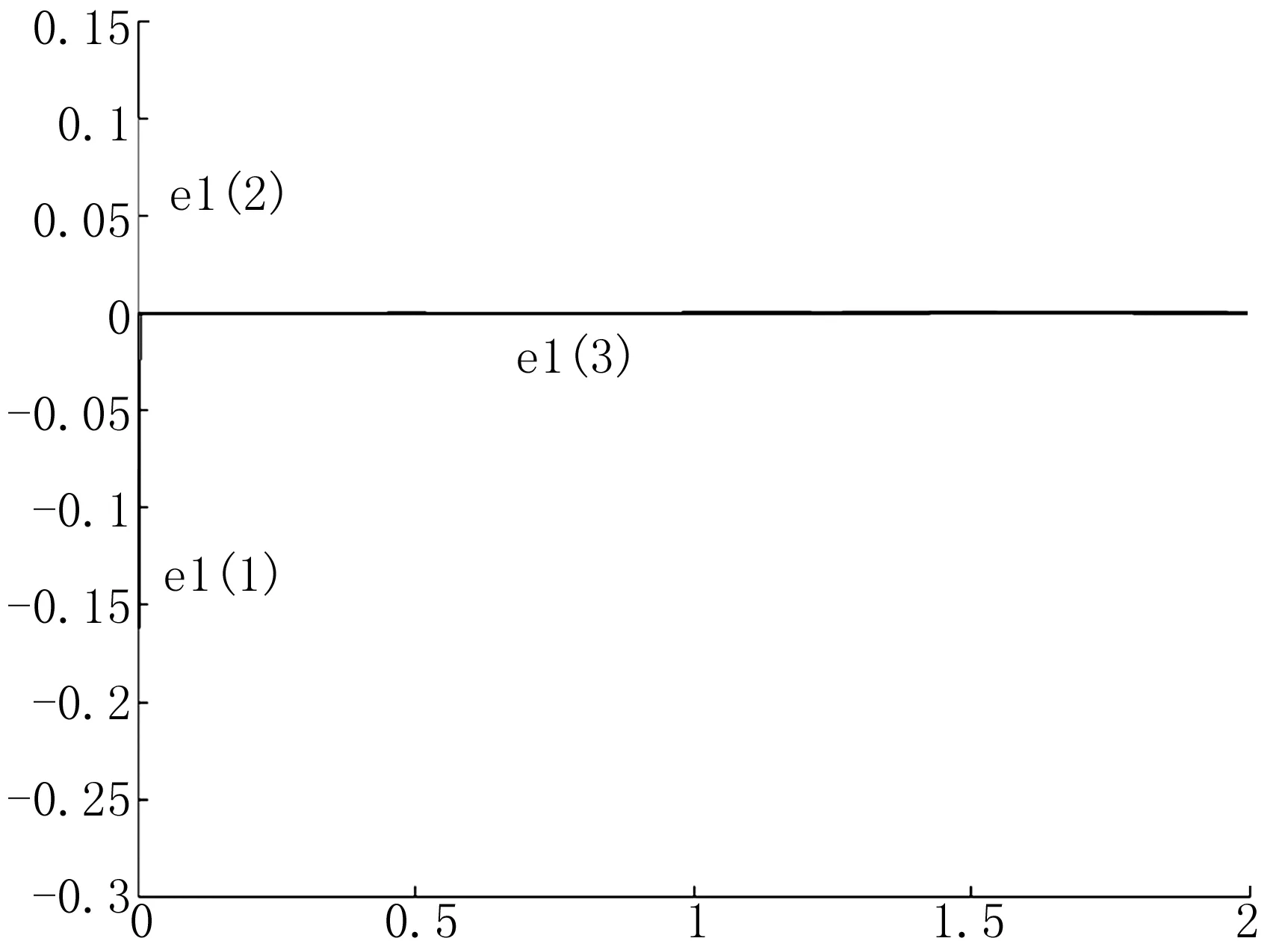
图和x之间的广义状态同步误差

图和y之间的广义状态同步误差

图8　y和x之间的广义状态同步误差

4　结语

通过使用辅助系统的方法，本文研究了具有时变多面体不确定和有界扰动的异构主从混沌系统的自适应广义同步控制。分别给出了非连续自适应律和连续自适应律两种方案。作为特例，文中还给出了完全状态同步的相关条件。数值仿真算例的结果表明，所提同步策略是有效的。

[1]PecoraLM，CarrollTL.Synchronizationinchaoticsystems[J].Phys.Rev.Letts.，1990，64(8)：821-827.

[2]BanerjeeT，BiswasD，SarkarBC.Completeandgeneralizedsynchronizationofchaosandhyperchaosinacoupledfirst-ordertime-delayedsystem[J].NonlinearDynamics，2013，71(1/2)：279-290.

[3]FekiM.Anadaptivechaossynchronizationschemeappliedtosecurecommunication[J].ChaosSolitons&Fractals，2003，18(1)：141-148.

[4]LuJ，WuX，HanX，etal.Adaptivefeedbacksynchronizationofaunifiedchaoticsystem[J].PhysicsLettersA，2004，329(4)：327-333.

[5]YuY，ZhangS.Adaptivebacksteppingsynchronizationofuncertainchaoticsystem[J].ChaosSolitons&Fractals，2004，21(3)：643-649.

[6]ChaiY，ChenLQ.Projectivelagsynchronizationofspatiotemporalchaosviaactiveslidingmodecontrol[J].CommunicationsinNonlinearScienceandNumericalSimulation，2012，17(8)：3390-3398.

[7]ChenS，LuJ，Synchronizationofanuncertainunifiedchaoticsystemviaadaptivecontrol[J].ChaosSolitons&Fractals，2002，14(4)：643-647.

[8]LiN，PanW，YanL，etal.Enhancedchaossynchronizationandcommunicationincascade-coupledsemiconductorringlasers[J].CommunicationsinNonlinearScienceandNumericalSimulation，2014，19(6)：1874-1883.

[9]WangCC，SuJP.Anewadaptivevariablestructurecontrolforchaoticsynchronizationandsecurecommunication[J].ChaosSolitons&Fractal，2004，20(5)：967-977.

[10]AbarbanelHDI，RulkovNF，SushchikMM.Generalizedsynchronizationofchaos：Theauxiliarysystemapproach[J].PhysicalReviewE，1996，53(5)：4528.

[11]WuGC，BaleanuD.Chaossynchronizationofthediscretefractionallogisticmap[J].SignalProcessing，2014，102：96-99.

[12]LiaoTL，TsaiSH.Adaptivesynchronizationofchaoticsystemsanditsapplicationtosecurecommunications[J].ChaosSolitons&Fractals，2000，11(9)：1387-1396.

[13]WangXingyuan，WangMingjun.Adaptiverobustsynchronizationforaclassofdifferentuncertainchaoticsystems[J].InternationalJournalofModernPhysicsB.，2008，22(23)：4069-4082.

[14]LalescuCC，MeneveauC，EyinkGL.Synchronizationofchaosinfullydevelopedturbulence[J].Physicalreviewletters，2013，110(8)：084102.

[15]PPourmahmoodM，KhanmohammadiS，AlizadehG.Synchronizationoftwodifferentuncertainchaoticsystemswithunknownparametersusingarobustadaptiveslidingmode[J].CommunicationsinNonlinearScienceandNumericalSimulation，2011，16(7)：2853-2868.

[16]YuK，QiangL，KunpengL，etal.Twoapproachesofadaptivesynchronizationforchaoticsystemswithdiversestructures[C]//ControlConference2013 32ndChinese.Xi’an：IEEE，2013：3110-3113.

[17]YuY，LiHX.Adaptivegeneralizedfunctionprojectivesynchronizationofuncertainchaoticsystems[J].NonlinearAnalysis：RealWorldApplications，2010，11(4)：2456-2464.

[18]KebriaeiH，JavadYazdanpanahM.Robustadaptivesynchronizationofdifferentuncertainchaoticsystemssubjecttoinputnonlinearity[J].CommunicationsinNonlinearScienceandNumericalSimulation，2010，15(2)：430-441.

[19]OdibatZM.Adaptivefeedbackcontrolandsynchronizationofnon-identicalchaoticfractionalordersystems[J].NonlinearDynamics，2010，60(4)：479-487.

[20]ChengCC，LinYS，WuSW.Designofadaptiveslidingmodetrackingcontrollersforchaoticsynchronizationandapplicationtosecurecommunications[J].JournaloftheFranklinInstitute，2012，349(8)：2626-2649.

[21]ZhangR，YangS.Adaptivesynchronizationoffractional-orderchaoticsystemsviaasingledrivingvariable[J].NonlinearDynamics，2011，66(4)：831-837.

[22]LinC，WangQG，LeeTH.Alessconservativerobuststabilitytestforlinearuncertaintime-delaysystems[J].IEEETransactionsonAutomaticControl，2006，51(1)：87-91.

[23]LiuX，FengS，MaM.RobustMPCfortheconstrainedsystemwithpolytopicuncertainty[J].InternationalJournalofSystemsScience，2012，43(2)：248-258.

[24]ZhangL，WangJ，LiC.Distributedmodelpredictivecontrolforpolytopicuncertainsystemssubjecttoactuatorsaturation[J].JournalofProcessControl，2013，23(8)：1075-1089.

The Synchronization Control for Different Chaotic Systems with Polytopic Uncertainty and Bounded Noise

ZHANG Zhi-qun，etc.

(DepartmentofElectronicEngineering，FujianPolytechnicofInformationTechnology，Fuzhou350003，China)

The topic on adaptive synchronization control for different chaotic systems with time-varying polytopic uncertainty and bounded noise is investigated.For the heterogeneous feature in master-slave system，by using auxiliary system method，the general synchronization continuous-time control laws and non-continuous time control laws have been given in master-slave chaotic systems.As a special case，the sufficient conditions for complete synchronization in master-slave system are also given in this paper.Finally，the effectiveness of the obtained are verified by numerical simulation results.

polytopic uncertainty；heterogeneous chaotic systems；adaptive control synchronization

10.3969/j.issn.1009-8984.2016.03.024

2016-05-23

张智群(1969-)，男(汉)，吉林松原，讲师，硕士

主要研究电路与系统。

TP273

A

1009-8984(2016)03-0105-06