基于三维物质点法的SSMSSF建筑结构体系研究

赵明华

(安徽广播电视大学马鞍山分校，安徽 马鞍山 243000)



基于三维物质点法的SSMSSF建筑结构体系研究

赵明华

(安徽广播电视大学马鞍山分校，安徽 马鞍山 243000)

基于新兴的三维物质点法，针对多层钢结构模块建筑实际工程(北京某水电医院办公大楼)，提出新型的多层钢结构模块——刚结构复合框架建筑结构体系(Storey Steel Module-Composite Structures Of Steel Frame Construction System，SSMSSF建筑结构体系)，并利用Mathematica软件进行了模型构建。根据SSMSSF建筑结构体系节点的受力特点，研究在不同的荷载、工况下，对SSMSSF建筑结构体系进行分析计算，研究其中的应力、位移情况。结果显示：传统钢结构的设计方法可以被完美移植到SSMSSF建筑结构体系设计中，由此而得到的应力、位移结果满足规范要求。

多层钢结构；SSMSSF建筑结构体系；三维物质点法；节点受力

0　引言

多层钢结构建筑的设计是建筑领域广泛关注的问题[1]。随着经济的发展以及原有建筑的不断迭代更新，基于多层钢结构的模块化建筑体系的研究课题越来越受到国内外学者的关注[2]。

国内外学者对于多层钢结构建筑的研究主要分为两个方面：实验法和数值模拟法[3-4]。实验法主要是利用小比例建筑施压模型进行长期实验，并观测其中的相关数据，但实验法对于实验条件要求苛刻，难以设置对照实验，无法对同种对象进行重复实验，并且许多数据是难以观测的[5-6]；数值法避免了实验法难以观测数据的缺点，并且可以随意重复试验，是当下应用较为广泛的一种研究多层钢结构建筑设计问题的方法[7]。但是，传统意义上的数值方法(无论是Lagrangian法还是Eulerian法)，都有自身难以克服的缺陷：Eulerian法不易追踪物质的边界；Lagrangian法会产生网格畸变[8]。

新兴的物质点法在时间、空间、尺度上可以与实验结果相比较，并且结合了Eulerian法和Lagrangian法的优点，避免了其缺点[9-13]。本文采用新兴的三维物质点法，针对多层钢结构模块建筑实际工程(北京某水电医院办公大楼)，提出新型的多层钢结构模块——刚结构复合框架建筑结构体系(Storey Steel Module-Composite Structures Of Steel Frame Construction System，SSMSSF建筑结构体系)，并利用Mathematica软件构建了三维钢结构模型。通过改变模型的参数，模拟不同荷载、工况，将得到的应力、应变情况与规范相比较。验证三维物质点法在多层钢结构建筑问题中的适用性，以期为实际工程的设计、施工提供参考。

1　工程概况

北京市某水电医院办公大楼位于北京市丰台区，距离永定门7.6 km，总建筑面积为253 673.2 m2。建筑层数为3层，局部为4层。建筑高度17.21 m。其中首层层高为5.5 m。其余标准层高为3.9 m，因地下有地铁通行，故而并未设置地下空间，属多层建筑，结构形式为SSMSSF建筑结构体系。

1.1结构体系

钢结构模块的尺寸要求：钢结构模块必须在特定的工厂内进行加工制作，出厂之后不允许在工地私自更改形状和尺寸。模块单元的宽度大部分在2.5～3.5 m之间，极个别大于3.5 m，但不会超过4.2 m[14-16]。

功能要求：第一层有模块展示区、咖啡厅；第二层有通向隔壁工厂的天桥。

1.2模块单元划分

为了具体描画建筑的每一个细节，将整栋建筑划分成51个模块单元，每个模块单元的长度均在7.7～8.1 m，宽度均在2.3 m～4.5m，高度约3.8 m。图1和图2分别展示了建筑平面图和模块划分图。

图1　建筑平面图

图2　模块分区图

1.3模块类型

钢结构模块(图3)可以分为普通模块单元、中柱模块单元、支撑模块单元、角部加强模块单元。其中，图3(a)为普通模块单元，包含了4根模块柱、地板梁、天花板梁、次梁；图3(b)为中柱模块单元，即在普通模块单元的基础上增设中柱；图3(c)为支撑模块单元，即在模块单元内设置支撑；图3(d)为支撑模块单元，即在模块建筑角部。

1.4模块类型

第一层采用的是H型钢梁，并添加了矩形钢管。梁柱节点的形式采用的是隔板贯通式。两柱之间全部采用栓焊混接，如此受力的性能比较好，安装的时候也比较方便。

1.5构件设计

本工程要求使用的钢材全部为Q345B钢。第一层柱截面有φ200×10，φ310×200×10，φ310×10 3种类型。模块梁截面φ100×50×5～φ300×150×10不等。与模块柱相连的梁截面宽度为150 mm。

(a)普通模块单元

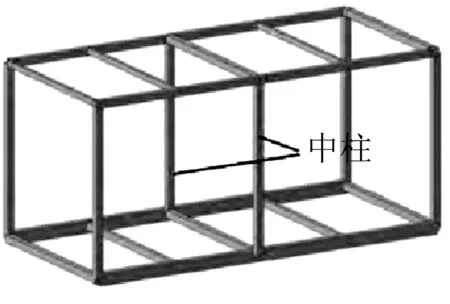
(b)中柱模块单元

(d)角部加强模块单元图3　模块的类型(Mathematica模型)

1.6传统钢框架与模块单元之间的连接节点

图4展现了传统钢框架与模块单元之间的连接节点的形式，为了增强传统框架与模块单元之间的牢固性，增加了垫块、插销连接架等结构。

图4　连接点

2　物质点法的基本思想

物体在开始时刻t=0所处的空间为初始构型Ω0，随着物体的运动，在时刻t所处的空间为现时构型Ω。任意选择一个时刻的构型作为参考构型。则在参考构形中，任意一个质点的矢径X可以表示为

X=Xieii=1，2，3，

(1)

式中：ei为参考构型的基矢量；Xi为X在3个坐标轴上的投影，称为Lagrangian坐标。

在现时构形中，任意一个矢径X可以表示为

X=xieii=1，2，3，

(2)

式中：ei为参考构型的基矢量；xi为X在3个坐标轴上的投影，称为Eulerian坐标。

质点X运动方程可以表示为

xi=xi(X,t)。

(3)

在Lagrangian描述和Eulerian描述中，质点X的位移分别为

ui=xi(X，t)-Xi，

(4)

ui=xi-Xi(X,t)。

(5)

质点的速度为式(4)中的Lagrangian导数，即

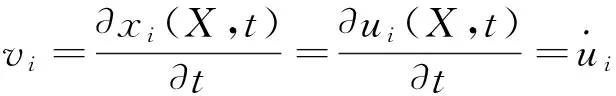
(6)

质点的加速度为式子(6)中的Lagrangian导数，即

(7)

在Eulerian描述中，物理量F=F(x，t)=F(x(X，t)，t)，F的Lagrangian导数为

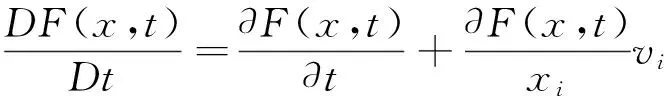
(8)

式中：∂F(x,t)/∂t为Eulerian导数；vi∂F(x,t)/xi为迁移导数。

Eulerian坐标xi对Lagrangian坐标Xi的偏导数称之为变形梯度。在初始构型中，任意两个质点X和X+dX的变形为

(9)

换算成矩阵形式

(10)

现时构型中的体积为

dV=JdV0，

(11)

所以

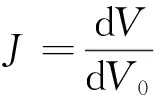
(12)

假设质点p，p′的坐标分别为xj，xj+dxj，则p′相对于p的速度为

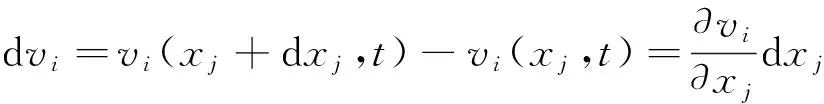
(13)

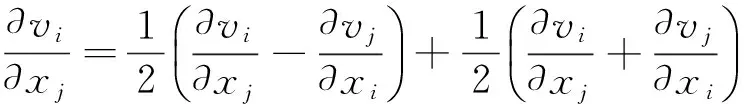
(14)

令

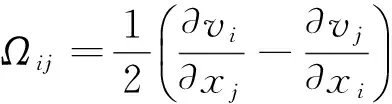
(15)

(16)

并称Ωij为旋转张量，称Dij为变形率张量，联立式(13)～(16)，得到

dvi=Ωijdxj+Dijdxj。

(17)

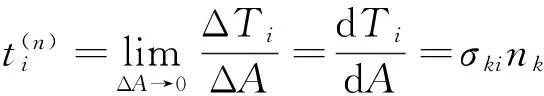
(18)

式中σij为Cauchy应力张量，且是对称的，

σij=σji。

(19)

控制方程为：

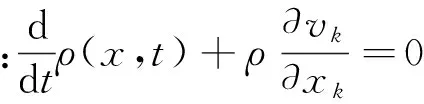
(20)

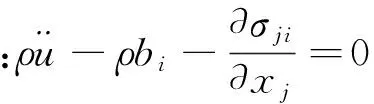
(21)

(22)

(23)

(24)

(25)

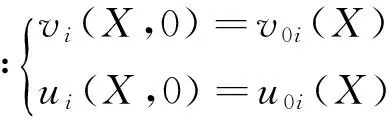
(26)

式中Γt、Γu分别为面力边界和位移边界，σji是Cauchy应力。

对于弹性模型

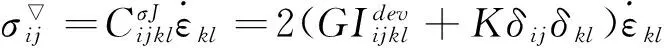
(27)

式中：G为剪切模量；K为体积模量。

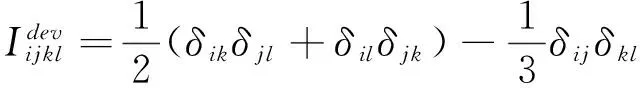
(28)

取两个对称偏张量sij和εij，有

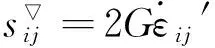
(29)

(30)

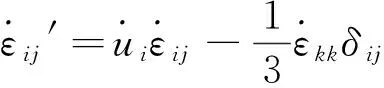
(31)

故而，弹性模型的更新格式为

(32)

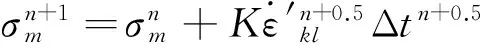
(33)

Johnson-Cook模型可以展现材料的高应变率。屈服应力为

(34)

Johnson和Cook二人将屈服应力表示为

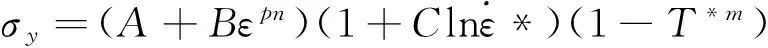
(35)

材料参数。

多方过程满足

(36)

式中：n为多方气体指数；ρ0为参考密度。

不可压缩流体状态方程为

(37)

式中p0为参考压强。

线性多项式状态方程为

p=c0+c1μ+c2μ2+c3μ3+(c4+c5μ+c6μ2)E，

(38)

式中c0～c6为材料常数。

Mie-Gruneisen状态方程为

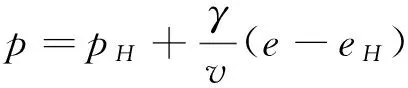
(39)

式中pH和eH分别为Hugoniot曲线上的压力和比内能。

p-α状态方程为

(40)

式中：α为孔隙率；v为比体积；e为比内能。

3　模型构建

表1中，ρ为材料密度，E为杨氏模量，ν为泊松比，A、B、n、C、m为材料常数。物质点的半径为1 cm，网格间距为1.4 cm，共1 652 346 254 656个物质点。根据建筑的设计要求，可抵抗8级地震，分组为第一组，基本的地震加速度为0.2g；建筑场地的类别为Ⅳ类，其特征周期为0.65 s，基本风压强为0.56 kN/m2。参考GB50009—2012《建筑结构荷载规范》，需要计算恒荷载、活荷载、风荷载和地震的作用效果。

表1　钢架的材料参数

4　结果分析

4.1周期和振型

图5展现了8根梁或16根梁的节点域和前12阶的振型分布情况。根据图5，前3阶的振型频率较低而4～12阶的振型频率变化幅度较大；除第5、9、12阶发生了细微的局部震动，其余的全部为整体震动。综上所述结构刚度分布较为合理，模块建筑整体性较强。

(a)节点域

(b)前12阶的振型分布图5　节点域和振型分布图

图6展现的是前3阶的周期和振型的情况，第一阶振型为x方向平动，周期为0.842 s。第二节振型则变为y方向振动，周期变为0.542 s。第三节振型变为扭动振型，周期为0.515 s。总体而言，第三节振型周期除以第一阶振型周期小于规定的0.85，满足工程要求。

(a)第一阶振型(T1=0.842 s)

(b)第二阶振型(T2=0.542 s)

(c)第三阶振型(T3=0.515 s)图6　前3阶振型和周期

4.2顶点位移

图7展现的是不同工况下的顶点位移情况。其中DLWX表示在X方向添加风荷载；DLWY表示在Y方向添加风荷载;DLRX表示在X方向添加地震作用；DLWY表示在Y方向添加地震作用。根据图7展示的情况，最大的位移均发生在最高层。其中DLWX工况下的最大位移为5.6 mm；DLWY工况下的最大位移为6.3 mm;DLRX工况下的最大位移为30.0 mm；DLWY工况下的最大位移为20.3 mm。4种工况下的最大位移均小于GB 50017—2003《钢结构设计规范》[17]中32.8 mm的限值要求。

(a)DLWX工况下X方向位移(5.6 mm)

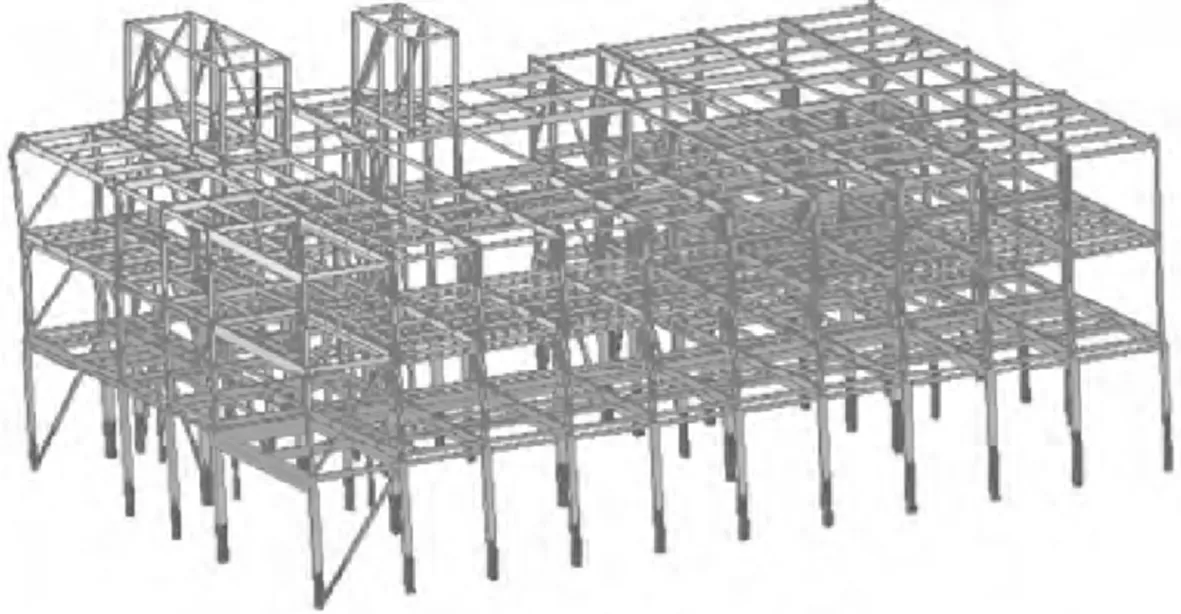
(b)DLWY工况下Y方向位移(6.3 mm)

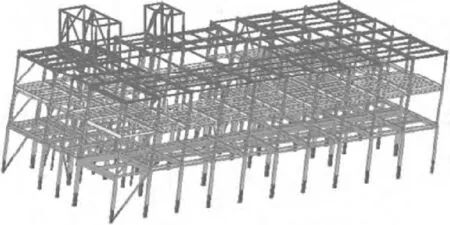
(c)DLRX工况下X方向位移(30.0 mm)

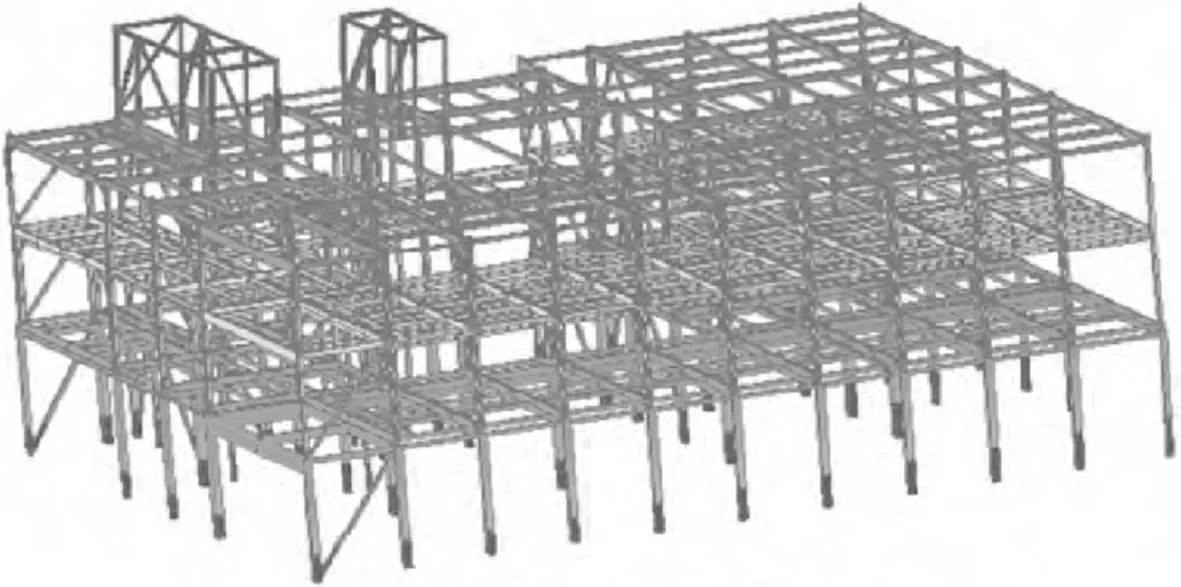
(d)DLRY工况下Y方向位移(20.3 mm)图7　不同工况下的顶点位移

4.3位移角和位移比

图8展现的是不同工况下层间位移角和位移比的情况。根据图8可以看出，在风荷载和地震的作用下，最大层间的位移角发生在X向地震作用下的2层，为1/318。最大的位移比为1.32，发生在Y相地震作用下的3层。这两个结果均满足规范[18-21]要求。

(a) 层间位移角

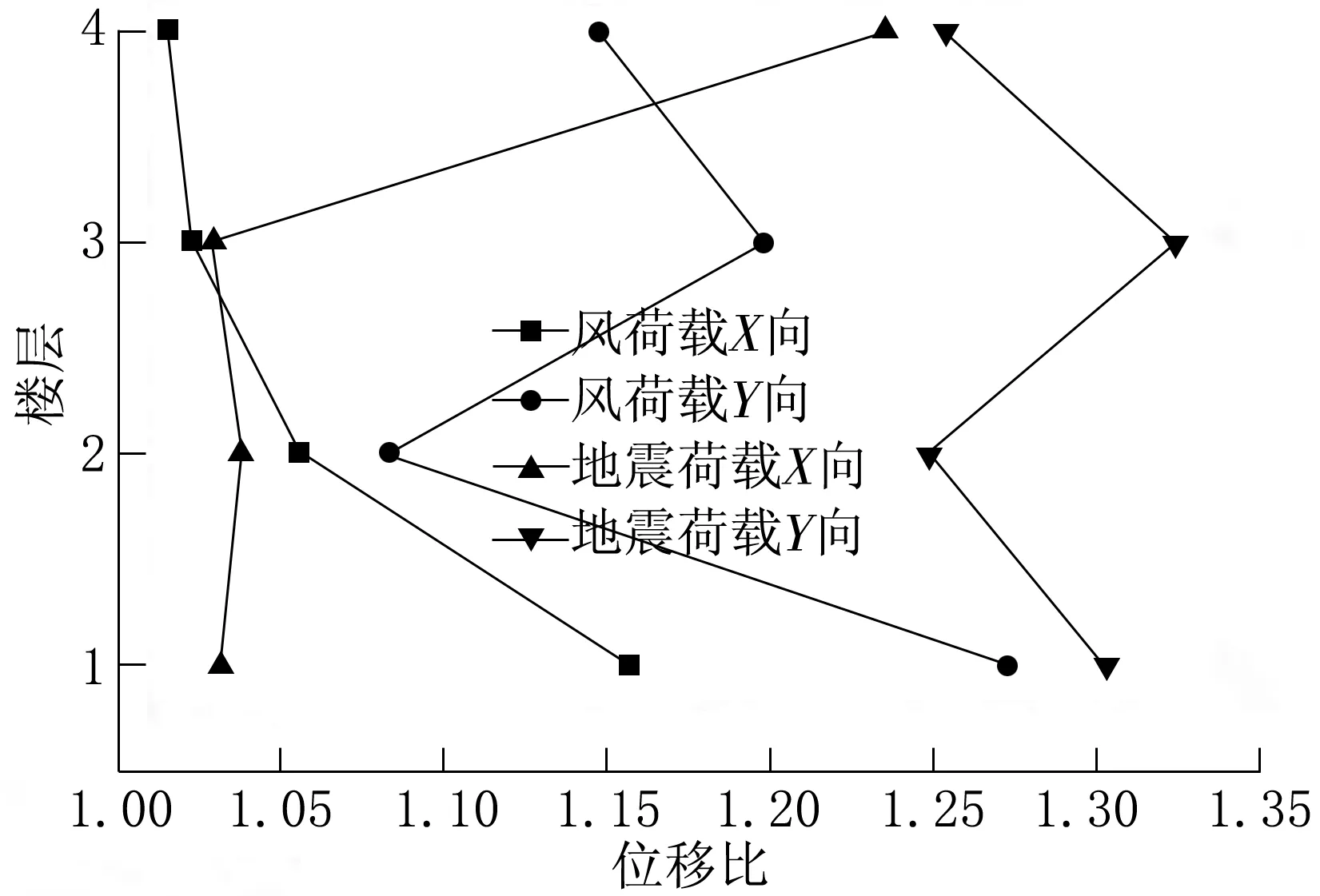
(b) 位移比图8　层间位移角和位移比

4.4应力比和用钢量

图9展现的是钢构件应力比和混凝土构件应力比，根据图9(a)的展示，钢构件应力比均小于1，且绝大部分都在0.87以下，最大的应力比为0.88，满足工程规定[17-20]。根据图9(b)展示的混凝土构件应力比情况，混凝土构件的应力比均小于1，且绝大部分也在0.8之下，最大的应力比为0.95，满足工程规定[17-20]。经过计算，结构的总用钢量为216 610 kg，平均每平方米用钢量为85.6 kg。用钢量略高于传统钢架结构，但其流水线作业及其环保的性能足以弥补该缺憾[21]。

4.5弹性时程

图10展现的是层间位移角和顶点位移时程曲线。模型选取的是El Centro波，设置最大加速度为0.07g。根据图10展示的结果，最大层间位移角出现在2层X方向，大小为1/326，满足工程规定[17-20]；根据顶点位移时程曲线可知，最大顶点位移发生在x方向，为30.4 mm，小于32.8 mm，满足工程规定[17-20]。

(a) 钢构件应力比

(b) 混凝土构件应力比图9　应力比

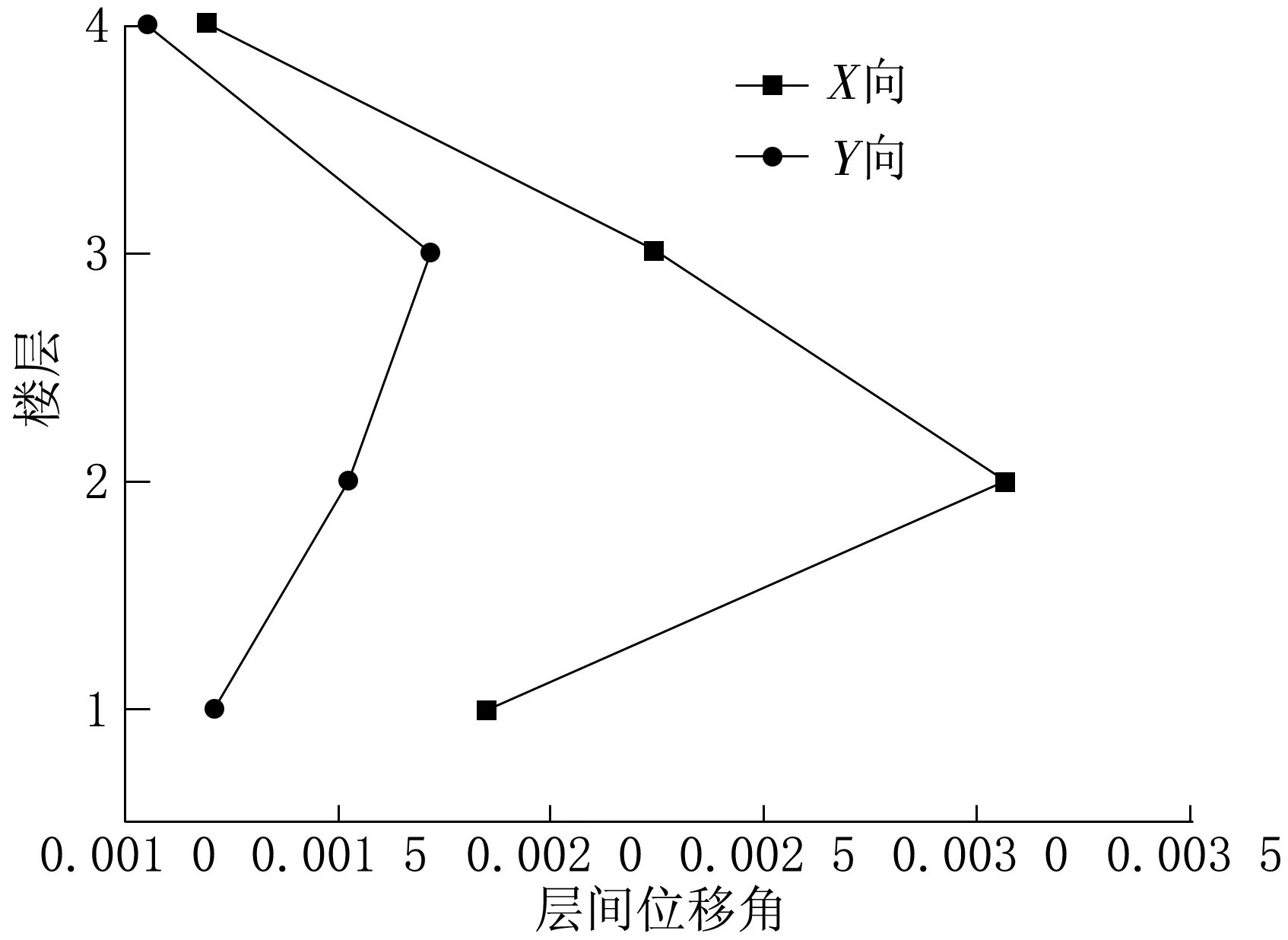
(a) El Centro波作用下的层间位移角

5　结语

本文基于新兴的三维物质点法，针对北京某水电医院办公楼实际工程，提出了SSMSSF建筑结构体系，对其中的钢结构模块单元进行了详细的阐述，并描述了不同的钢结构模块单元的具体形式，最后就振型和周期、顶点位移、位移角和位移比、位移比和用钢量、弹性时程进行了数值刻画，结果显示：

1)三维物质点对于多层钢结构建筑的设计问题具有很强的适应性；

2)利用Mathematica软件进行模型构建，并利用三维物质点法进行计算，结果显示振型和周期、顶点位移、位移角和位移比、位移比和用钢量都满足工程需求。

3)在El Centro波的作用下研究弹性时程，就地震验算方面，层间位移角和顶点位移时程满足工程需求。

[1] Georgios S，Papavasileiou，Dimos C，et al.Seismic design optimization of multi-storey steel-concrete composite buildings[J].Computers & Structures，2016，170:49-61.

[2] Yu Z，Ni J，Fang L，et al.Multilayer 3D structure made of modified stainless steel mesh for in-situ continuous separation of spilled Oil[J].Industrial & Engineering Chemistry Research，2015，54(47)：11838-11843.

[3] Zhu S，Wu Y，Liu T，et al.Interface structure and deuterium permeation properties of Er 2 O 3 /SiC multilayer film prepared by RF magnetron sputtering[J].International Journal of Hydrogen Energy，2015，40(16):5701-5706.

[4] Li B，Geng X，Lu T，et al.Experimental verification of the interface wave method to detect interlaminar damage of a metal multilayer structure[J].Frontiers of Mechanical Engineering，2015，10(4):380-391.

[5] Zhang R，Wang L.Synergistic improving of tribological properties of amorphous carbon film enhanced by F-Si-doped multilayer structure under corrosive environment[J].Surface & Coatings Technology，2015，276:626-635.

[6] Brunetti A，Golosio B，Melis M G，et al.A high-quality multilayer structure characterization method based on X-ray fluorescence and Monte Carlo simulation[J].Applied Physics A，2015，118(2):497-504.

[7] Kundrát V，Zhang X，Cooke K，et al.A novel Mo-W interlayer approach for CVD diamond deposition on steel[J].Aip Advances，2015，5(4):473.

[8] Aiguo Xu，Guangcai Zhang，Hua Li，et al.Dynamical similarity in shock wave response of porous material: From the view of pressure[J].Computers and Mathematics with Applications，2011，61: 3618-3627.

[9] XU Ai-Guo，PAN Xiao-Fei，ZHANG Guang-Cai.Material- point simulation of cavity collapse under shock[J].Journal of Physics：Condensed Matter，2007，19: 326212.

[10] PAN，X F XU Ai-Guo，ZHANG Guang-Cai，et al.Generalized interpolation material point approach to high melting explosive with cavities under shock [J].J.Phys.D:Appl.Phys.，2008，41:015401.

[11] PAN Xiao-Fei，XU Ai-Guo，ZHANG Guang-Cai，et al.Three-dimensional multi-mesh material point method for solving collision problems [J].Commun Theor Phys，2008，49(5):1129-1138.

[12] XU AiGuo，ZHANG Guang-Cai，Yang-Jun Ying，et al.Simulation study on cavity growth in ductile metal materials under dyn amic loading[J].Front.Phys.2013，8(4): 394-404.

[13] Cheng C C，Cheng T M，ChiangC H.Defect detection ofconcrete structuresusingboth infrared thermographyandelastic waves[J].Automation in Construction.2008，1 8(1)：8-92.

[14] 中国钢结构协会.CECS 334—2013 集装箱模块化组合房屋技术规程[S].北京:中国计划出版社，2013.

[15] 国绿空间模块装备(天津)有限公司.DBQ29-87—2014 钢结构模块建筑应用技术规程:[S].天津:国绿空间模块装备(天津)有限公司，2014.

[16] Lawson R M，Ogden R G，Bergin R.Application of modular construction in high-rise buildings[J].Journal of Architectural Engineering，2012，18(2):148-154.

[17] 中华人民共和国建设部.GB 50017—2003 钢结构设计规范[S].北京:中国计划出版社，2003.

[18] 中国建筑技术研究院.JGJ 99—98高层民用建筑钢结构技术规程[S].北京:中国建筑工业出版社，1988.

[19] 中华人民共和国建设部.GB 50011—2010 建筑抗震设计规范[S].北京:中国建筑工业出版社，2010.

[20] 中华人民共和国住房和城乡建设部.GB 50009—2012 建筑结构荷载规范[S].北京:中国建筑工业出版社，2012.

[21] Motavalli，Masoud，Ghafoori，et al.Method for pre-stressing a steel structure,and steel structure pre-stressed using said method[J].United states Patent Application,2016,14:98-101.

The Study SSMSSF on Building System Based on 3-D Material Point Method

ZHAO Ming-hua

(MaanshanCampus，AnhuiOpenUniversity，MaanshanAnhui243000，China)

Based on the new three-dimensional material point method for multi-layer steel modular building actual Engineering(an office building of a hydropower hospital in Beijing)，a new multilevel steel structure module-(Storey Steel Module-Composite structures of Steel Frame construction system，short for SSMSSF)has been proposed in this article.The model construction has been by using Mathematica software.According to the characteristics on different node forces，the analysis and algorithm to SSMSSF building structural system under different loads，conditions have been researched.The stress and displacement has been researched.The results show：the traditional steel design approach can be transplanted to the design of SSMSSF building system perfectly.The stress and displacement obtained can meet the specifications.

multilayer steel structure；SSMSSF building system；three-dimensional material point method；node force

10.3969/j.issn.1009-8984.2016.03.004

2016-06-06

赵明华(1969-)，女(汉)，安徽马鞍山，副教授

主要研究建筑项目管理。

TU391

A

1009-8984(2016)03-0016-07