基于多元组提高射频仿真角度精度的方法

唐　波, 盛新庆, 金从军, 赵小阳

(1. 北京科技大学计算机与通信工程学院, 北京 100083; 2. 北京理工大学电磁仿真中心, 北京 100081;3. 北京仿真中心, 北京 100037; 4. 中国人民解放军96610部队, 北京 100085)



基于多元组提高射频仿真角度精度的方法

唐波1, 盛新庆2, 金从军3, 赵小阳4

(1. 北京科技大学计算机与通信工程学院, 北京 100083; 2. 北京理工大学电磁仿真中心, 北京 100081;3. 北京仿真中心, 北京 100037; 4. 中国人民解放军96610部队, 北京 100085)

射频仿真技术在弹载射频系统的研发过程中发挥着重要作用,然而现有基于传统三元组的射频仿真系统角度精度的进一步提高存在瓶颈。研究了利用多元组结构来提高角度精度的方法,相较于传统的三元组,多元组的幅度取值存在冗余,可以通过优化求解,获得各辐射单元的最优的幅度取值,给出了在此最优幅度下多元组所能达到的最优仿真角度误差方差的表达式。数值计算结果表明,幅度优化后的多元组能够显著提高射频仿真系统的角度精度。研究结果对于射频仿真技术能力的提升具有理论意义和应用价值。

射频仿真系统; 三元组; 多元组; 角度精度

0　引　言

射频仿真技术在复杂电子系统的研发过程中发挥着重要的作用。特别是在军事电子领域,如导引头电子系统,半实物射频仿真显得尤为重要。真实的外场试验具有时间长、耗费高的特点。并且,若贸然进行外场试验,可能面临较高的失败风险。因而,在进行外场试验之前,进行射频仿真可以最大程度地减小外场试验的风险,达到减少外场试验次数以及费用的效果。正因如此,世界各主要军事强国皆建立有射频仿真实验室以资使用,例如美国陆军高级仿真中心,埃格林空军基地的导弹仿真实验室,英国马可尼公司等等[1-2]。我国也在航天工业部门和相关科研机构建立有射频仿真实验室。射频仿真也称为实物在回路仿真[3-4]。射频仿真的经典结构是三元组结构,这是波音公司提出的一种同时使用3个辐射单元来仿真一个点目标的结构[5]。通过控制3个辐射单元的馈电幅度的大小,来调整待仿真点目标的位置,从而实现运动点目标的仿真[6]。三元组结构的提出是射频仿真领域的一项具有开创性的工作,时至今日,仍是绝大部分射频仿真系统的首选。三元组的工作原理与多干扰辐射单元在多通道雷达中生成虚假目标信号的工作原理很相似[7],只不过此为合作目标,彼为非合作目标。三元组的三个单元一般呈正三角形排列,这是由于幅度相位误差所造成的仿真角度误差与三元组结构的尺寸呈现出正相关性,因此为了提高仿真角度精度,应在满足耦合隔离度要求下对辐射单元进行密集排列。密排的构型与单元口面的形态紧密相关。由于实际中所用单元口面常为正方形和圆,因此三元组的排列构型多采用正三角形。

对于射频仿真的学术研究,大部分的文献资料主要关注于仿真误差的计算[8-10]、近场效应的修正[11-12]、仿真置信度问题[13-17]、宽带仿真、多目标仿真、幅相控制和极化等[18-20]。由于射频仿真系统的核心功能是精确地模拟散射回波的方向,仿真角度误差是其重要性能参数,因而对仿真角度误差的分析和改进一直在实际的研究工作中受到重视。

在射频仿真系统中,产生仿真角度误差的因素有多种,包括幅度相位误差、近场误差、转台误差等。仿真角度误差可以分为随机误差部分和系统误差部分,随机误差主要通过提高幅度相位控制精度来改进,系统误差部分主要通过系统校正、近场修正来改进。而当角度精度提高到一定程度之后,再提升传统的三元组系统的角度精度是很困难的。因而本文引入一种新的方法来提高角度精度。该方法通过使用多个辐射单元,即多元组,来达到抑制随机误差的目的。对于多元组来讲,由于增加的辐射单元也会带来误差且其由于偏离目标点更远而使误差传递系数更大,这似乎只会带来更大的仿真角度误差,其实不然。从原理上讲,仅使用3个辐射单元就可以实现对动目标的仿真,若采用多元组,则存在系统冗余,本文通过优化求解获得各辐射单元的最优幅度取值,达到了抑制角度误差的目的。文中的数值结果表明,幅度优化后的多元组能够显著地提高射频仿真系统的角度精度。

1　多元组的辐射单元幅度计算

对于射频仿真来讲,关键的一步是要计算出各单元的幅度。为便于分析,图1给出了分析所用的坐标系统。图1展示了三元组中的第i个辐射单元与传感器口面的位置关系。在图1中,传感器口面位于xy平面内,坐标原点位于口面中心。第i个辐射单元位于Ui点。

图1　传感器口面坐标系Fig.1　Coordinates system of the sensor aperture

假设三元组的3个辐射单元的方向为(Θ1,Φ1),(Θ2,Φ2),(Θ3,Φ3),其中Θi趋于零;三元组仿真的点目标方向为(Θ0,Φ0)。记

(1)

(2)

(3)

(4)

则根据著名的幅度重心公式,应有

(5)

(6)

为了分析以及应用方便,在绝大部分的研究文献中,一般都令

(7)

则式(5)～式(7)可以联立为方程组。当针对三元组时,即N=3,此时容易解出[21]

(8)

(9)

且仿真角度误差为

(10)

(11)

下面据此来研究一下多元组。在多元组的情况下,幅度未知数的个数多于方程的个数,因而Ci的解是不唯一的。为了获得Ci的定解,在此需要考察其取值对误差传递的影响。此时N元组仿真角度误差的一般表示为

(12)

(13)

式中，N>3。对于多元组来讲,由于求和项增多以及结构尺寸变大所致的误差传递系数变大,似乎必然会令总误差增大。其实不然。由于Ci的解是不唯一的,因此可以通过选取合适的Ci的取值使该误差优于三元组的情况,即充分地利用了多元组的冗余特性。下面进行仿真角度误差的优化求解以确定Ci。

已知幅度误差ΔCi的方差可以表示为

(14)

式中,γ为幅度误差常系数。则两个方向上的仿真角度误差的方差分别为

(15)

(16)

则仿真角度误差的方差可以表示为

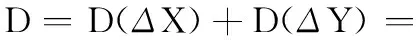
(17)

现在的问题转化为,式(5)～式(7)的约束条件下使式(17)取最小值。对此优化问题,可以使用经典的拉格朗日乘数法。令拉格朗日函数为

(18)

式中，λX,λY和λ1为拉格朗日乘数。将式(18)对Ci求导,并令其结果为0,得

(19)

将该组方程式与(5)～式(7)联立为方程组,该方程组具有N+3个未知数(Ci,λX,λY,λ1)和N+3个方程,因而可以解得

(20)

式中

(21)

ui=Xi-X

(22)

vi=Yi-Y

(23)

(24)

进一步地,可以将式(20)展开为

(25)

最后,可将式(20)代入式(17)以分析仿真角度误差的方差,得

(26)

这样,就获得了多元组的幅度解以及仿真角度误差的方差。下文进一步分析其性能。

2　多元组角度误差的数值分析

为了更详细地考察多元组带来的角度仿真精度的改进,在此进行数值计算分析。计算中所用参数如下。辐射单元在球面阵列上均匀分布,相邻单元相对于传感器的张角为24mrad,幅度误差常系数γ不妨设为0.01。实际上,由式(26)可知,仿真角度误差的方差与γ呈简单线性关系,误差的减小倍数与γ无关,仅与单元数以及空间结构有关。辐射单元编号如图2所示。计算针对的目标位置为处于单元1～3所组成的三角形内的区域。

图3给出了仅使用1～3号辐射单元所导致的仿真角度误差的方差分布，该计算基于式(25)、式(26)。误差为0的3个点即为1～3号辐射单元所在的方位位置。图4给出了使用1～6号辐射单元所导致的仿真角度误差的方差分布。图5给出了使用1～15号辐射单元所导致的仿真角度误差的方差分布。

图2　阵列中辐射单元编号Fig.2　Serial number of the unit

图3　传统三元组的仿真角误差的方差分布Fig.3　Error variance of three-unit-array

图4　六元组的仿真角误差的方差分布Fig.4　Error variance of six-unit-array

图5　十五元组的仿真角误差的方差分布Fig.5　Error variance of fifteen-unit-array

由图3～图5可以看到,随着所用单元数的增多,仿真角度误差的方差呈现下降的趋势。这表明,利用多元组确实可以改善角度仿真精度。这是因为,多元组的冗余特性可以被用来优化幅度的取值,从而减小角度误差。另外,可以看到, 1～3号辐射单元所在的方位位置处,六元组以及十五元组在该三点处的误差仍为0。

为了定量的分析多元组改善角度仿真精度的程度,图6、图7分别给出了图4、图5方差数据相对于图3方差数据的比值分布图。

图6　六元组方差对传统三元组方差的比值Fig.6　Ratio of six-unit-array error variance to three-unit-array

图7　十五元组方差对传统三元组方差的比值Fig.7　Ratio of fifteen-unit-array error variance to three-unit-array

图6中,该方差比值的最大值为0.856 3,最小值为0.698 9;图7中,该方差比值的最大值为0.742 2,最小值为0.539 9。考虑到仿真系统的性能参数是由角度误差最大值给出,因此还需要计算图4、图5方差数据最大值相对于图3方差数据最大值的比值,分别为0.714 4,0.558 8;对于均方根误差,则相应的比值为0.845 2,0.747 5。这意味着如果三元组的仿真角度随机误差为0.4mrad,则十五元组可以做到0.3mrad。虽然这种角度精度的改进不是数量级上的,但是考虑到角度精度改进的难度是随着精度提高而快速增加的,所以这种程度的改进也是很有意义的。事实上,根据相关资料分析,国内与国外在仿真角度精度的相对水平上相当于0.4mrad相对0.2mrad的水平,因此,能够做到0.3mrad也是从0.4mrad向0.2mrad的很大的一步进展。

3　多元组的近场修正

多元组仍然存在近场效应。若采用多元组仿真结构,则现有的基于三元组的近场效应修正流程需要重新审视。现有的基于三元组的修正采取的方法是,首先给出在相同的仿真环境下,真实口径传感器的测角与口径为0的理想传感器的测角之间的角度差,此角度差即为需要修正的角度。这样,在仿真时,由需要仿真的真实口径传感器的测角以及对应的角度差,得到口径为0的理想传感器的测角,再由重心公式得到三元组的幅度。而对于多元组,该流程基本适用,但是最后需依据式(25)来获得多元组的幅度。

虽然流程相同,然而如何获得该角度差、即角度修正量的大小,其方法和具体操作会有所不同。在传统的三元组的修正量计算中,需要通过不断地调整幅度来获得[22]。而对于多元组,由于单元数量较多,幅度变量会很多。若仍然采用调整幅度的方式,则复杂性增大很多。因此,多元组的近场修正角度量的获取,可以考虑采用更有效率的方式。具体做法如下。

首先给定一个口径趋于零的传感器的测量角度Ω0=(X0,Y0),由该角度依据式(25)来获得多元组的幅度Ci,由该多元组的幅度通过实验或电磁数值计算的方法来获得真实口径传感器的测量角度Ω=(X,Y)。则角度修正量为ΔΩ=Ω0-Ω,该修正量为X0,Y0的函数,这样就获得了修正表。当Ω0=(X0,Y0)为均匀采样时,Ω=(X,Y)一般是非均匀的。由于修正表的输入为Ω=(X,Y),为了方便实际使用,可以通过插值的方法使Ω=(X,Y)为均匀采样。这样,基于修正表,通过Ω→ΔΩ→Ω0→Ci的流程即可获得近场修正后的多元组的幅度。

修正量的计算为近场修正的关键部分。图8给出修正量ΔX对X0,Y0的函数关系的计算示例。计算中针对的传感器为基线长度为0.2m的二维干涉仪,工作波长为0.01m,使用十五元组。

图8　修正量ΔX的计算示例Fig.8　Correcting value of ΔX

4　结　论

为了探索进一步提高射频仿真系统的角度精度的途径,本文对多元组进行了原理性研究。结果表明,相比于传统的三元组,多元组的冗余特性可以用来提高角度仿真精度。通过将多元组的幅度求解问题建模为角度误差最小化的优化问题,使用拉格朗日乘数法获得了最优的幅度解。数值结果表明,在这样的最优幅度解下,可以使多元组的角度精度相较于三元组获得显著的提高。从本质上讲,虽然多元组所增加的辐射单元由于偏离仿真目标点较远,进而使误差传递系数较大,但是通过优化,可以赋予这些辐射单元较小的幅度加权,从而使总误差减小。给予较大的误差源以较小的加权。这与信号处理中的匹配滤波法具有异曲同工之处,原理上其实是相通的。所以,多元组仿真,具有原理上的正确性与合理性。

而对于多元组的近场修正问题,根据本文的分析,其也可以较好地解决。但是,原有的三元组修正表将不能被继续使用,需要重新建立多元组的近场修正表。而对于其他的一些系统误差,如,转台中心的位置偏差,也不会因使用多元组而变差。实际上,若在优化方程中考虑系统误差修正后的残差,使用多元组可以进一步使系统误差减小。因此,多元组的使用也具有一定的工程可行性,值得进一步深入研究和采用。

[1]XiYW,ZhangJH,GaoWJ,etal.LowcostHILSsystemofRadarseekerandapplication[J]. Fire Control Radar Technology, 2010,39(1):11-15.(习远望,张江华, 高文冀, 等.雷达导引头低成本半实物仿真系统的应用[J].火控雷达技术,2010,39(1):11-15.)

[2]HWILinUSEglinAFBfor20years[J]. Winged Missiles Journal，1999(3):41-45.(美国埃格林空军基地半实物仿真试验20年[J].飞航导弹,1999(3):41-45.)

[3]McPhersonDA.NearfieldangleerrorcompensationforhighprecisionHWILRFmissileseekersimulation[C]∥Proc. of the 16th Century Society & Conference, 1993: 640-645.

[4]BishopCB.ErroranalysisofpointtargetsinHWILsimulation[C]∥Proc. of the 16th Century Society & Conference, 1994: 373-378.

[5]PolkinghorneAA.Radiofrequencysimulationsystem(RFSS)systemdesignhandbook[R].USA:BoeingCompany, 1975.

[6]ZengJK.Theresearchofthetargetsimulationinradiofrequencysimulationsystem[D].Nanjing:NanjingUniversityofScienceandTechnology, 2003. (曾建奎. 射频仿真系统中目标仿真方法研究[D]. 南京:南京理工大学, 2003.)

[7]TangB,GuoKY,WangJP.The3DactivedeceptionjammingofSAR[J]. Acta Electronica Sinica, 2007, 35(6):1203-1206. (唐波, 郭琨毅, 王建萍. 合成孔径雷达三维有源欺骗干扰[J]. 电子学报,2007,35(6):1203-1206.)

[8]CaiL,DaiGL,LuTJ.Erroranalysisandcompensationofradiofrequencysimulationtargetimitationsystem[J]. Computer Engineering and Design,2007,28(15):3672-3674.(蔡磊,戴革林,陆廷金.射频仿真目标模拟系统误差分析及补偿[J].计算机工程与设计,2007, 28(15): 3672-3674.)

[9]HaoXJ,ChenYG,HeJG,etal.Analysisofplanewaveerrorinradiofrequencysimulationsystem[J]. Journal of Henan University of Science and Technology: Natural Science, 2008,29(5):50-53.(郝晓军,陈永光,何建国,等. 射频仿真系统平面波误差分析[J].河南科技大学学报:自然科学版,2008,29(5):50-53.)

[10]LiY,ZhaoJC,QuYH.Newmethodofimprovingsurface-arraypositioningaccuracyinRFSS[J]. Science Technology and Engineering, 2009, 9(8):2201-2203.(李勇,赵军仓,曲艺海. 一种提高射频仿真系统面阵精度的新方法[J]. 科学技术与工程, 2009, 9(8):2201-2203.)

[11]ChenXD.Thedualnearfieldeffectinradiofrequencysimulation[J]. Journal of System Simulation, 2001, 13(1): 92-95. (陈训达. 射频仿真中的双近场效应[J]. 系统仿真学报, 2001, 13(1): 92-95.)

[12]LiuTS,JinCJ.VerifyingmethodofnearfielderrorcompensationofRFSS[C]∥Proc. of the 3rd China Guidance Navigation and Control Conference,2010：99-103.(刘天舒,金从军. 近场效应修正算法有效性验证方法[C]∥第三届中国导航、制导与控制学术会议论文集, 2010：99-103.)

[13]BiY.Erroranalysisofmissile’shardware-in-the-loopsimulationsystem[D].Xi’an:NorthwesternPolytechnicalUniversity, 2006. (毕业.导弹半实物仿真系统误差分析[D]. 西安:西北工业大学,2006.)

[14]ZhengMG,JiaoP.Credibilityassessmentofsimulationresultsofmissilesimulationsystem[J]. Computer Simulation, 2008, 25(2):83-86. (张明国,焦鹏. 导弹仿真系统试验结果的可信性评估[J]. 计算机仿真,2008,25(2):83-86.)

[15]ZhaYB,HuangKL,ZhangJK.Credibilityofmissilesystemsimulationanditsapplicationintestevaluation[J]. Journal of System Simulation,1997,9(1):10-17.(查亚兵,黄柯棣,张金槐.导弹系统仿真的可信性及其在试验鉴定中的应用[J].系统仿真学报,1997,9(1):10-17.)

[16]GuanRX,TaoYH.Analysisofaccuracyandcredibilityofsimulationexperiment[J]. Measurement&Control Technology, 1995, 14(5):7-10.(管如恂,陶渝辉.仿真系统精度与置信度分析[J].测控技术,1995,14(5):7-10.)

[17]WeiHL,LiuZZ.Crossspectralestimationanditsapplicationtosimulationmodelsvalidationformissilesystems[J]. Journal of System Simulation,1997,9(3):116-121.(魏华梁,刘藻珍.交叉谱估计及其在导弹系统仿真模型验证中的应用[J].系统仿真学报,1997,9(3):116-121.)

[18]HanXD,LiangZH,YanZ.Theradiofrequencysimulationofmultiplescatteringpointinradartargetmodel[J]. Computer Engineering and Applications, 2011, 47(8S):249-254. (韩晓东, 梁志恒, 颜漳. 多散射点雷达目标模型的射频仿真模拟[J]. 计算机工程与应用,2011,47(8S):249-254.)

[19]QiZ,FeiYC,ChenN,etal.Anewmodelingofradartargetbasedonmulti-scatteringcentersandimplementationofradartargetHWILsimulationsystem[C]∥Proc. of the International Conference on Microwave and Millimeter Wave Technology, 2008: 212-215.

[20]HeQR.Radiofrequencysimulationsystemwithmultiplechannels,widefieldandhighaccuracy[C]∥Proc. of the 11th International Congress on Stereology, 2003:314-315.(何秋茹.多通道、大视场、高精度射频仿真系统[C]∥第十一届国际体视学大会,2003:314-315.)

[21]TangB,ShengX,JinC,etal.Angleerroranalysisofmultiple-targetHWILRFSS[C]∥Proc. of the Target and Environment Modeling and Simulation Technology Conference in China, 2015:145-154.

[22]JiangQP.Theresearchonbroadbandactive/passiveradiofrequencysimulation[D].Xi’an:NorthwesternPolytechnicalUniversity, 2006.(蒋庆平.宽带主/被动射频仿真技术研究[D]. 西安: 西北工业大学,2006.)

Improving the angle accuracy of the RFSS based on multiple-radiating-unit array

TANG Bo1, SHENG Xin-qing2, JIN Cong-jun3, ZHAO Xiao-yang4

(1. School of Computer and Communication Engineering, University of Science and Technology Beijing,Beijing100083,China; 2.CenterforElectromagneticSimulation,SchoolofInformationandElectronics,BeijingInstituteofTechnology,Beijing100081,China; 3.ScienceandTechnologyonSpecialSystemSimulationLaboratory,Beijing100037,China; 4.Unit96610ofthePLA,Beijing100085,China)

The radio frequency simulation system (RFSS) is important for the research and development of the airborne radio frequency electronics system, and it is difficult to improve the angle accuracy of the RFSS with conventional three-radiating-unit array. The method of improving the angle accuracy of the RFSS by using the multiple-radiating-unit array instead of the conventional three-radiating-unit array. Comparing with the conventional three-radiating-unit array, the amplitudes of the units in the multiple-radiating-unit array cannot be determined only by the locations of the target and the units. Therefore, the optimization model is built to minimize the angle error. With the result of the optimized amplitudes, the expression of the angle error is given for the multiple-radiating-unit array. Based on the numerical computation results, it can be seen that the angle error of the multiple-radiating-unit array is decreased obviously compared with that of the conventional three-radiating-unit array. It is significant for the improvement of the angle accuracy of the RFSS further.

radio frequency simulation system (RFSS); three-radiating-unit array; multiple-radiating-unit array; angle accuracy

2016-01-13；

2016-06-26；网络优先出版日期：2016-08-05。

国家自然科学基金(61471041)；中央高校基本科研业务费专项资金(FRF-TP-15-028A3)资助课题

TN 97

A

10.3969/j.issn.1001-506X.2016.10.30

唐波(1978-),男,讲师,博士,主要研究方向为射频仿真、电子对抗。

E-mail:tangbohr@hotmail.com

盛新庆(1968-),男,教授,博士,主要研究方向为电磁仿真。

E-mail:xsheng@bit.edu.cn

金从军(1970-),男,研究员,博士,主要研究方向为射频仿真。

E-mail:cjunjin@sina.cn

赵小阳(1979-),男,工程师,主要研究方向为电子对抗、信息系统仿真。

E-mail:jialin0312@126.com

网络优先出版地址：http:∥www.cnki.net/kcms/detail/11.2422.TN.20160805.1524.006.html