超长基线双基机载雷达空时杂波建模与特性

王成浩, 廖桂生, 许京伟, 曾　操

(1. 西安电子科技大学雷达信号处理国家重点实验室, 陕西 西安 710071;2. 信息感知技术协同创新中心, 陕西 西安 710071)



超长基线双基机载雷达空时杂波建模与特性

王成浩1,2, 廖桂生1,2, 许京伟1,2, 曾操1,2

(1. 西安电子科技大学雷达信号处理国家重点实验室, 陕西 西安 710071;2. 信息感知技术协同创新中心, 陕西 西安 710071)

超长基线双基机载雷达杂波的空时分布特性不仅严重依赖于双基雷达构型,也取决于地球曲率引入的波束覆盖问题。针对这一问题,推导了地心坐标系下超长基线双基机载雷达等距离环解析表达式,得出等距离环在基线所在铅锤面的投影为抛物线。通过对几种典型双基构型及其公共波束覆盖区域的分析,研究了超长基线双基雷达杂波空时分布的条带式截断特性,给出了杂波分布的距离依赖性分析。仿真实验验证了本文分析结论的正确性和有效性。

超长基线; 双基机载雷达; 空时杂波; 杂波建模; 杂波特性

0　引　言

双基机载雷达能够有效实现地面和空中运动目标检测,在机载预警、战场监视与侦察等方面具有重要应用,受到国内外学者的广泛关注。相比于单基机载雷达而言,双基机载雷达系统具有覆盖范围广、作用距离远、接收机隐蔽等诸多优势[1-2]。双基地机载雷达通过增加基线长度将大大提高雷达系统的探测能力,具有重要的理论和应用价值。

双基机载雷达在运动目标检测过程中面临严重的杂波干扰,微弱目标信号将完全湮没在杂波背景中。并且双基机载雷达的杂波特性比单基雷达复杂得多,其分布特性受双基构型(如速度、高度及天线配置等)的影响显著,且存在严重的距离依赖性[2-3]。空时自适应处理(space-time adaptive processing, STAP)能够利用空间和时间自由度,有效实现杂波的抑制。实际中,杂波的分布特性会严重影响STAP方法的性能[4-9],因此,杂波特性的研究对于机载雷达运动目标检测具有重要意义。双基机载雷达杂波特性随距离空变,无法得到足够的独立同分布(independent and identically distributed, IID)样本,致使STAP方法性能严重下降[5-10],角度多普勒补偿方法(angle Doppler compensation, ADC)[6]通过两维补偿提高样本一致性,导数更新方法(derivative based updating, DBU)[8]认为自适应权是距离的函数,通过更新不同距离的权值来适应杂波的距离依赖性。目前,双基机载雷达模型中,中短基线情况下通常考虑地面为平面[3-4,11];长基线情况仅根据发射机和接收机的地平线距离确定有效地面散射区域而仍采用水平地面的假设[12]。实际上,对于长基线情况,特别是超长基线情况(基线长度在400～600 km),一方面地面弯曲带来的模型误差对于杂波特性的研究不可忽略(忽略地球曲率将造成高度误差达7 km),另一方面公共波束覆盖的有效地面散射区域对杂波空时分布特性的影响严重。因此,现有的长基线双基机载雷达模型不能准确描述超长基线双基机载雷达杂波分布特性,需要进一步考虑地球曲率对双基几何构型和杂波特性的影响,为后续STAP方法设计奠定基础。

本文充分考虑地球曲率对超长基线双基机载雷达系统构型和杂波散射区域的影响,对超长基线双基机载雷达杂波分布特性进行了研究。不同于文献[11,13]中转换到极坐标下的复杂推导,本文利用坐标系旋转变换方法推导了超长基线双基机载雷达等距离环在地心直角坐标系下的解析表达式,分析得出:等距离环在由基线和地心决定的平面上的投影是一条抛物线。通过对几种典型双基构型的分析,受公共照射区域的限制,杂波的空时分布具有条带式截断特性,截断部分是两段孤立的谱线,并且杂波分布具有严重的距离依赖性。

1　超长基线双基机载雷达构型

图1给出了超长基线双基机载雷达的工作场景示意图。实际上,当基线长度长达400～600 km量级时,必须在几何模型中考虑地面弯曲对杂波建模的影响,否则最大地面高程误差会高达约7 km。考虑地面为球面建立地心直角坐标系:以地心为原点,接收机所在直线为Z轴,基线所在平面为XOeZ平面建立地心坐标系OeXYZ如图1所示。设基线与X轴夹角为γ,基线长度为L,发射机与接收机的高度分别为HT和HR;速度分别为VT和VR;速度与X轴夹角分别为δVT和δVR,逆时针为正;发射机与接收机天线轴线相对速度方向偏角分别为δAT和δAR;散射点S相对发射机与接收机的速度锥角分别为φT和φR;发射机与接收机到散射点S的斜距分别为RT和RR;发射机与接收机相对地心的夹角为θe。

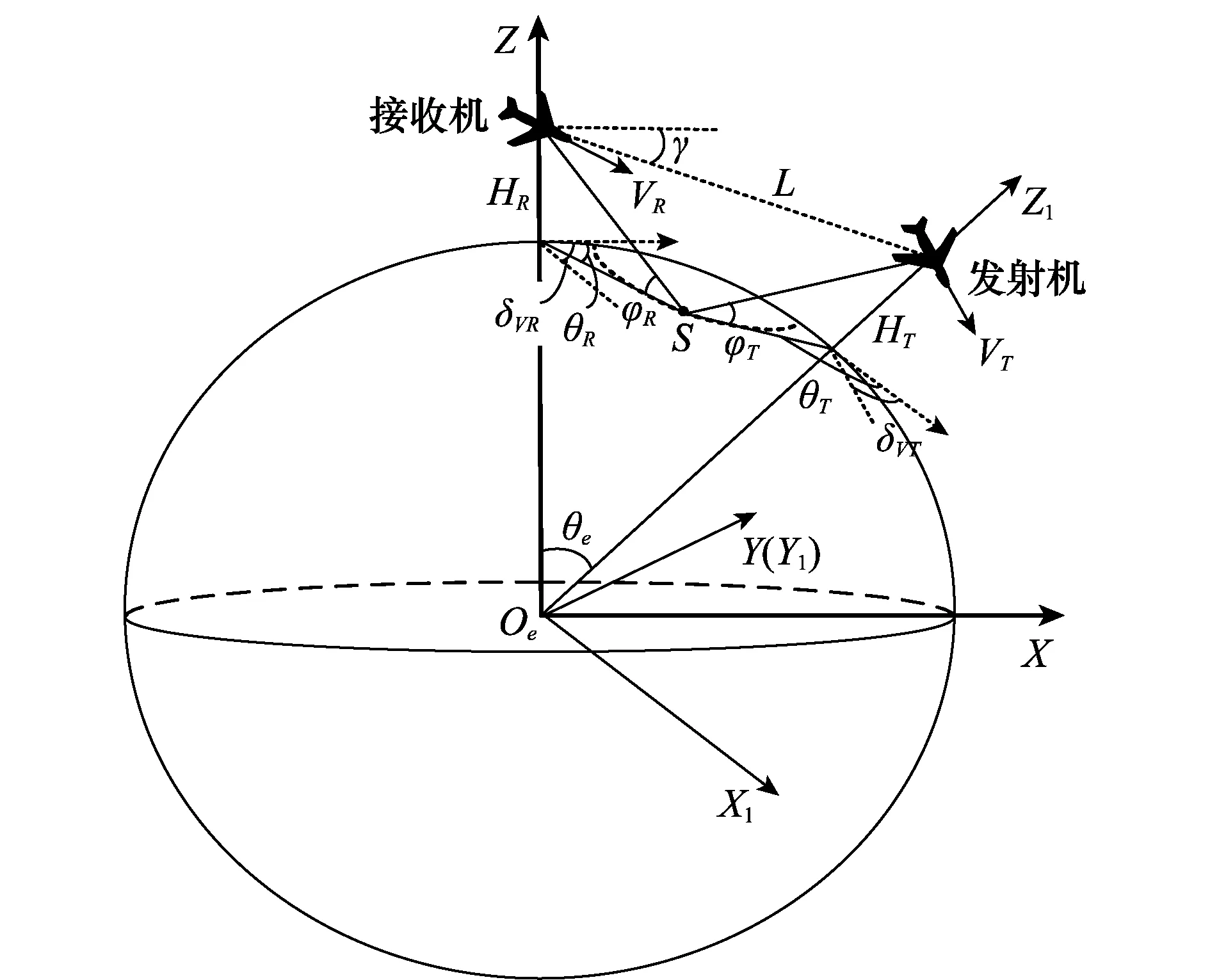
图1　超长基线双基机载雷达几何构型Fig.1　Geometry of ultralong baseline bistatic airborne radar

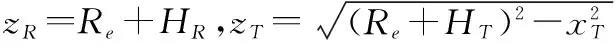
(1)

受地球曲率的限制,发射机和接收机的最大可视斜距分别为

(2)

地面上的任意散射点S(x,y,z)的双基距离为其到发射机与接收机距离之和,即

(3)

且散射点S满足地球表面的球面方程

(4)

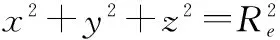
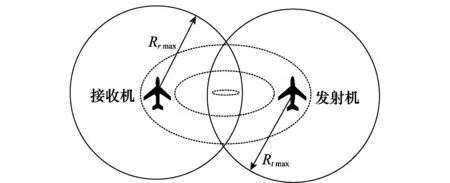
图2　杂波有效散射区域Fig.2　Effective clutter scattering region

2　超长基线双基机载雷达空时杂波建模与分析

对于双基雷达系统,等距离环上所有散射点的回波叠加形成该距离门回波信号,然而双基雷达等距离环的求解相比单基雷达更加复杂,在考虑地球曲率情况下,等双基距离环是一条三维空间中的曲线,求解双基雷达等距离环的解析表达式是杂波建模的难点,并且对信号建模和杂波特性分析至关重要,下面求解其解析表达式。

所有双基距离为Rs的散射点分布在同一个椭球面上,该椭球面以发射机和接收机为焦点,以Rs为长轴长,其标准方程可表达为

(5)

式中

为表达简洁,将式(5)中的常量做如下变量代换

(6)

则椭球面方程(5)可写作

(7)

由于双基雷达等距离环是式(7)代表的椭球面与地面的交线,因此需要联立方程式(4)和式(7)以求解其表达式

(8)

文献[13]在双基星载雷达的情况下,将直角坐标系转换到极坐标系来求解该方程,计算复杂,本文直接在地心直角坐标系下采用坐标系变换方法简洁地推导出了等双基距离环的解析表达式。将方程组(8)第2式代入第1式消去y,即将等距离环曲线投影到OeXZ平面,则方程组(8)等价于

(9)

为进一步揭示变量x与z的关系,将OeXYZ坐标系绕Y轴旋转角度γ得OeX1Y1Z1坐标系,在该坐标系下基线将与X1轴平行。原坐标系中的点(x,y,z)在新坐标系OeX1Y1Z1下可表示为

(10)

因此可得式(9)代表的等距离环在OeX1Y1Z1坐标系下的表达式为

(11)

对式(11)第1式进行适当整理得

(12a)

(12b)

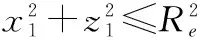
(13)

(14)

式(14)所示二次方程的系数为

(15)

求解式(14)可得

从而抛物线的定义域为

根据方程组(12)可得OeX1Y1Z1坐标系下任意等距离环上散射点的坐标(x1,y1,z1),对其做式(10)的逆旋转变换即可将其还原到OeXYZ坐标系下的坐标(x,y,z)，即

(16)

根据上述模型仿真计算得到等距离环曲线如图3和图4所示,仿真结果验证了模型的正确性和有效性。

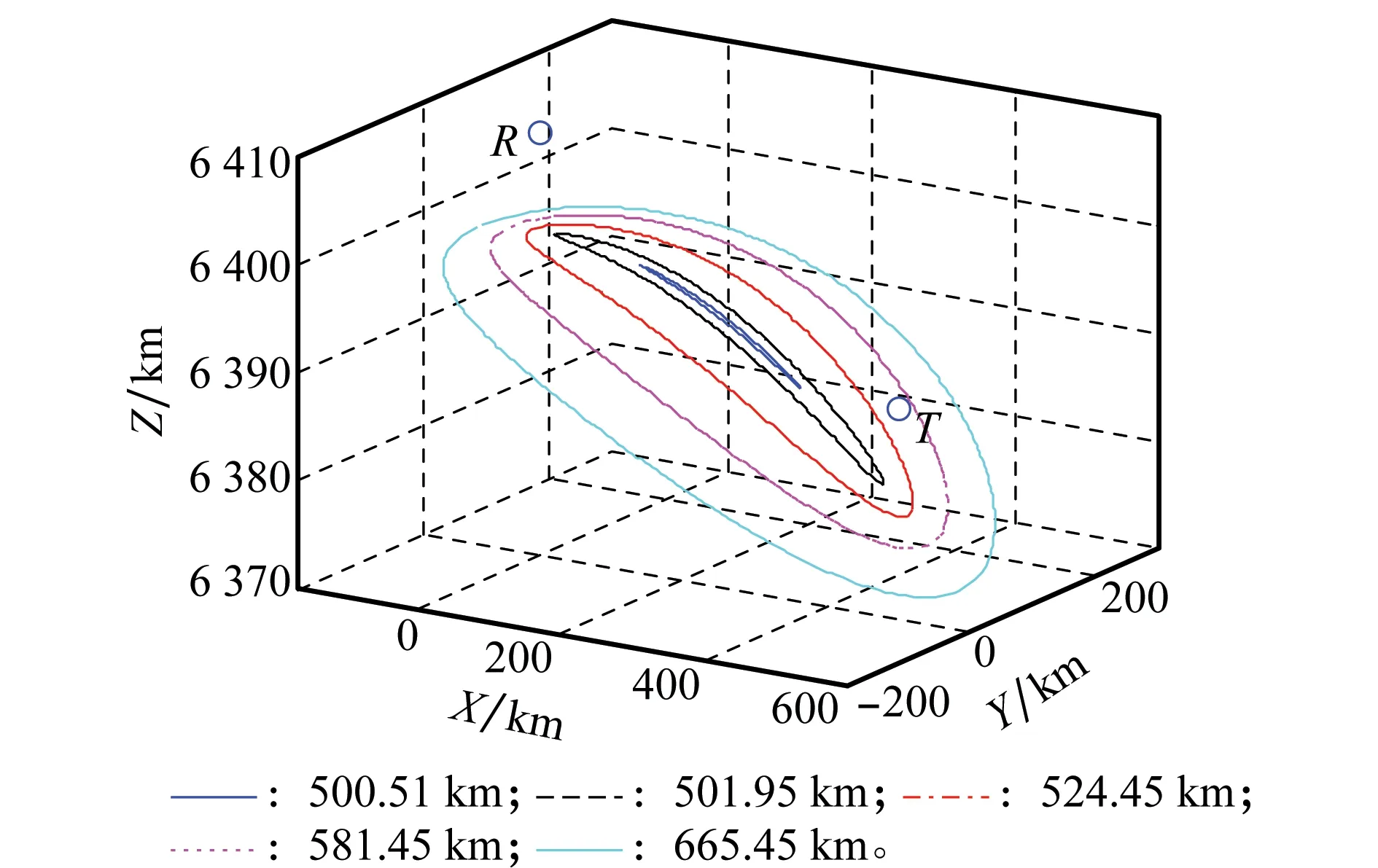
图3　地心直角坐标系下的等距离环Fig.3　Iso-range rings in geocentric cartesian coordinate

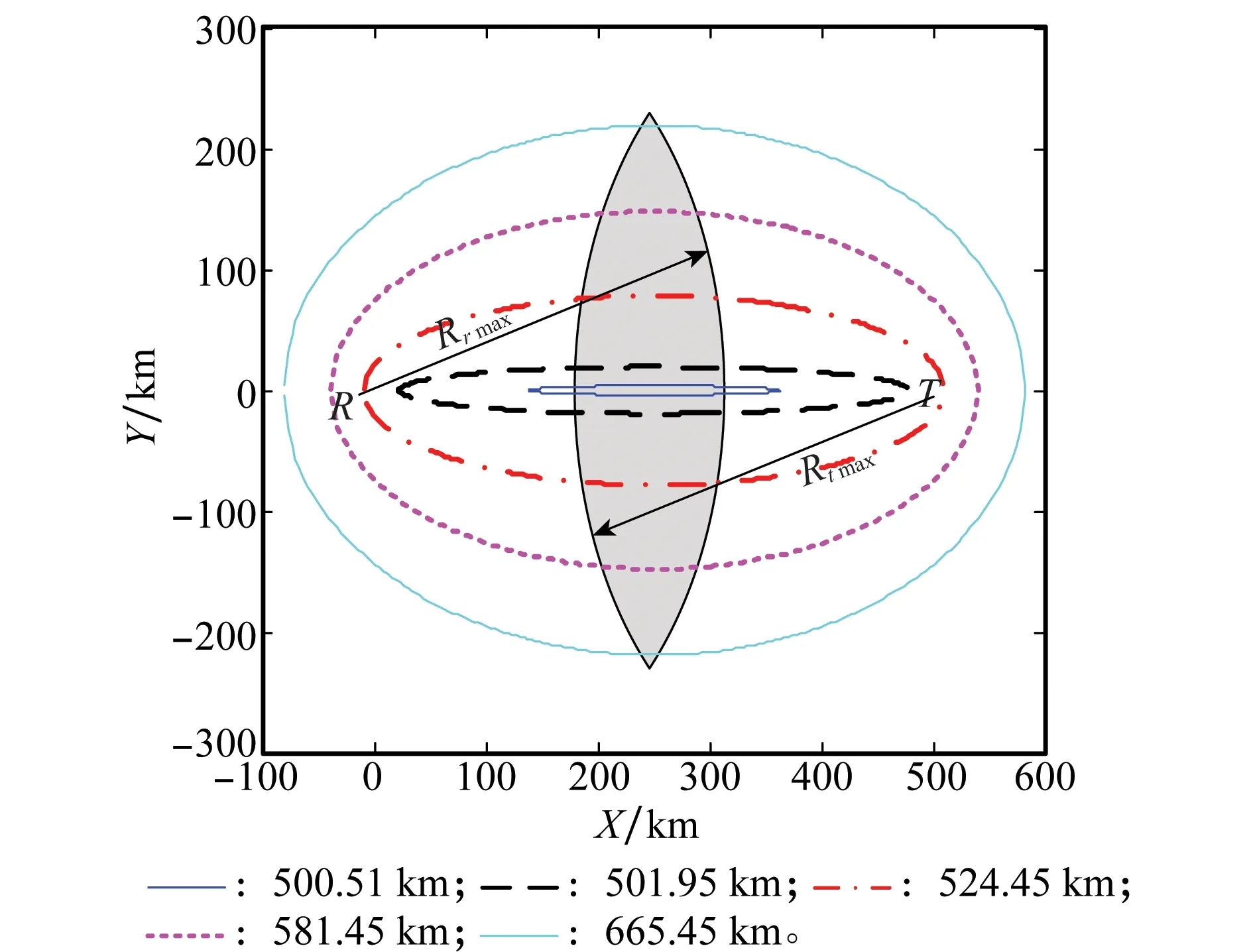
图4　等距离环与公共照射区域的关系Fig.4　Relationship between iso-range rings and the common illumination region

通过上述模型得到散射点的坐标(x,y,z)后,其空间角频率和多普勒角频率可表示为

(17)

式中,“·”为矢量内积；λ为波长；fPRF为脉冲重频；d为接收阵列的阵元位置矢量，即

(18)

式中，dant为接收阵列的阵元间距。

式(17)中，kr和kt分别为散射点相对接收机和发射机的单位传播矢量

(19)

式中，rt=(x-xt,y,z-zt)T；rr=(x,y,z-zr)T。假设发射机和接收机的速度平行于地面,在各自坐标系下其速度矢量分别为vtt=VT(cosδVT,sinδVT,0)T和vrr=VR(cosδVR,sinδVR,0)T。但考虑地球曲率影响,发射机坐标系相对接收机坐标系旋转了角度θe,因此地心坐标系下的发射机速度矢量为

(20)

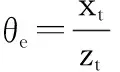
根据上述空时频率的计算结果可以得到实际回波模型,第l个距离门的第n个阵元第k次脉冲的回波为同一距离环上所有散射点回波的叠加

(21)

式中，A(θR)为θR方位散射点回波的复幅度,需要注意A(θR)在有效散射区域以外全为零。本节针对地球曲率及公共波束覆盖区域对杂波模型的影响,推导了超长基线双基机载雷达等距离环的解析表达式及杂波信号模型,得出不同于地平假设下的超长基线双基机载雷达等距离环在基线所在铅垂面的投影为抛物线。本节所得杂波信号模型能够满足超长基线双基机载雷达杂波建模要求,能够准确真实地描述实际杂波回波,下面根据上述模型进行仿真实验并重点分析杂波特性,为进一步设计有效的STAP方法奠定基础。

3　杂波仿真及特性分析

本节以3种典型的双基构型为例,首先从杂波的空时分布、杂波功率谱及其随距离变化情况等角度出发,分析超长基线双基地机载雷达的杂波特性,其次分析了接收机偏航对杂波特性的影响,最后综合本节实验结果给出结论。为便于比较分析,下文所有仿真均采用统一的系统参数,具体系统参数设置如表1所示。

表1　系统参数

3.1发射机与接收机平行飞行

在这种双基构型下,发射机与接收机均垂直于基线方向平行飞行。图5选取了有效散射区域覆盖到的若干距离门,其中图5(a)为整个地面范围杂波的多普勒-角度耦合特性曲线,图5(b)为有效散射区域杂波的多普勒-角度耦合特性曲线。

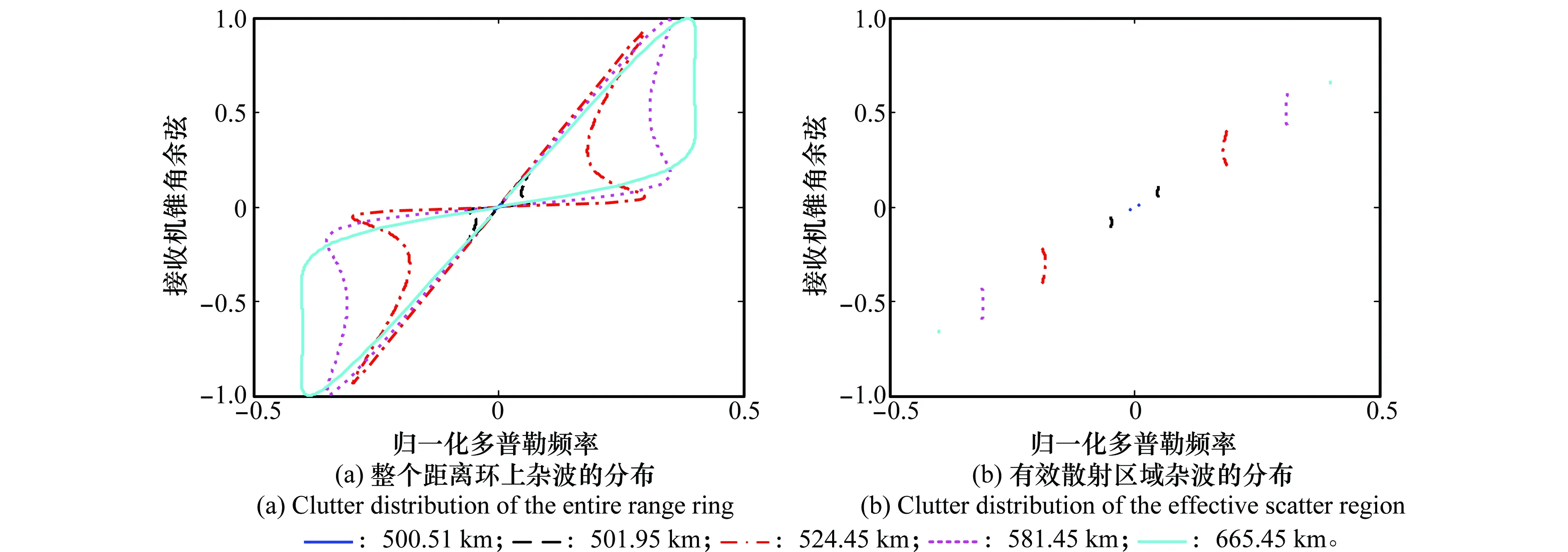
图5　平飞构型下杂波的空时分布Fig.5　Space-time clutter distribution of parallel geometry

一方面,图5(a)和图5 (b)所示杂波的空时分布特性随距离变化十分显著,表现出严重的距离依赖性;另一方面,在任意给定距离单元,图5(b)所示超长基线双基机载雷达杂波曲线不再连续,而是被一条带状区域截断为两段孤立的谱线,并且图5(b)中被截断部分对应于图5(a)中距离依赖性最强的区域。虽然杂波分布的条带式截断特性使单一距离门的杂波展宽范围大大缩小,但这部分杂波的距离依赖性是整个地面最严重的部分,这会对超长基线双基机载雷达杂波抑制方法带来严重问题。

下面通过仿真实验分析杂波功率谱特性。通过对一个CPI内的单通道数据做30dB切比雪夫加权的插值傅里叶变换,得到如图6所示的杂波的距离多普勒功率谱。图6所示的杂波功率谱存在明显的特点:单个距离的杂波在分布在两个孤立的区域内,且该区域位置随距离增加迅速向两侧移动。图7为所有距离门杂波最小方差无矢真响应(minimumvariancedistortionlessresponse,MVDR)功率谱平均的结果。图7直观反映了整个距离范围所有杂波在空时平面的分布情况,据仿真结果可见所有距离杂波被限制在同一条带内,杂波分布呈条带式截断特性,这也验证了图5对杂波空时分布特性的分析结果。

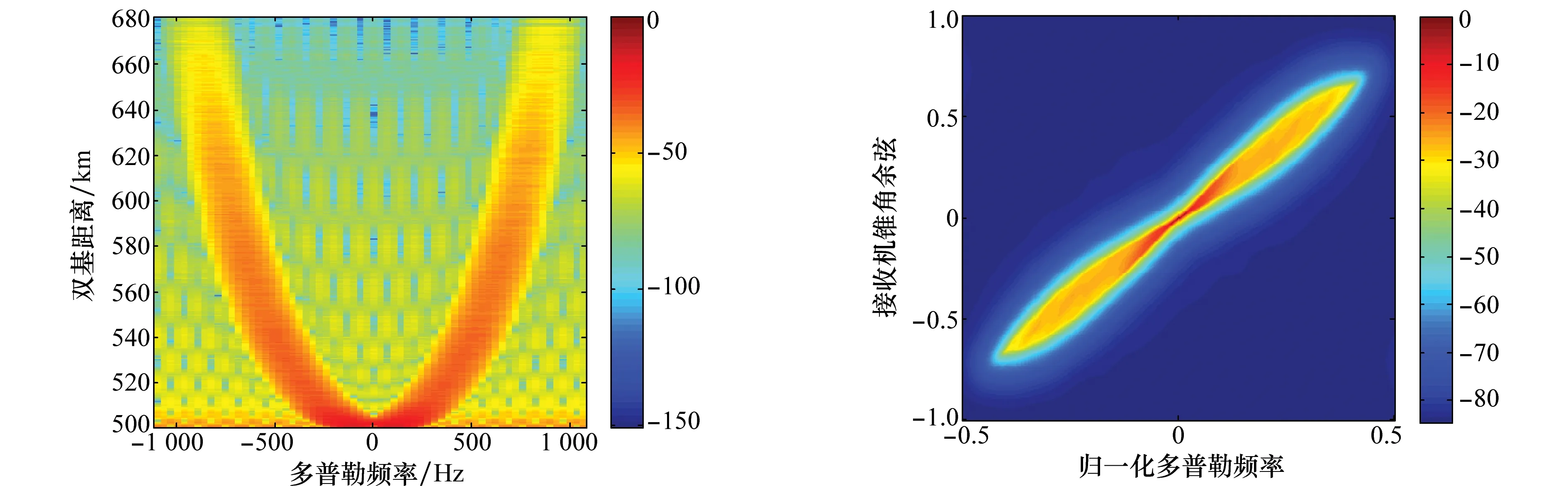
图6　平飞构型下的距离多普勒杂波谱　　　　　　　　　　　　　图7　平飞构型下距离平均的空时杂波谱　　　　　　　Fig.6　Range-Doppler clutter spectrum of parallel geometry　　　　Fig.7　Average space-time clutter spectrum of parallel geometry

图6和图7分别从不同方面反映了超长基线双基机载雷达杂波的条带式截断特性,这是双基构型和有效散射区域共同作用的结果:不同于传统双基机载地雷达,地球曲率限制了发射机和接收机的有效散射区域,因此对接收机形成干扰的杂波仅来自于该区域,杂波的条带式截断特性本质上来自于有效散射区域对等距离环的截断效应。可合理推测杂波谱所在条带区域的大小与有效散射区域的大小直接相关。

为进一步分析杂波的距离依赖性,以近程506.21km,中程536.18km和远程656.18km为例,给出不同距离处杂波的空时功率谱如图8所示。通过仿真实验得到杂波加噪声的真实协方差矩阵,从而采用MVDR方法得到图8所示杂波的空时功率谱。相比图5(b)所示不同距离杂波的空时耦合关系,图8(a)和图8(b)所示杂波谱的位置与理论分析相符,验证了杂波模型的有效性。对比图8(a)～图8(c)所示功率谱可得,杂波在3个距离处的空时分布发生了巨大的变化,同样反映了杂波严重的距离依赖性。

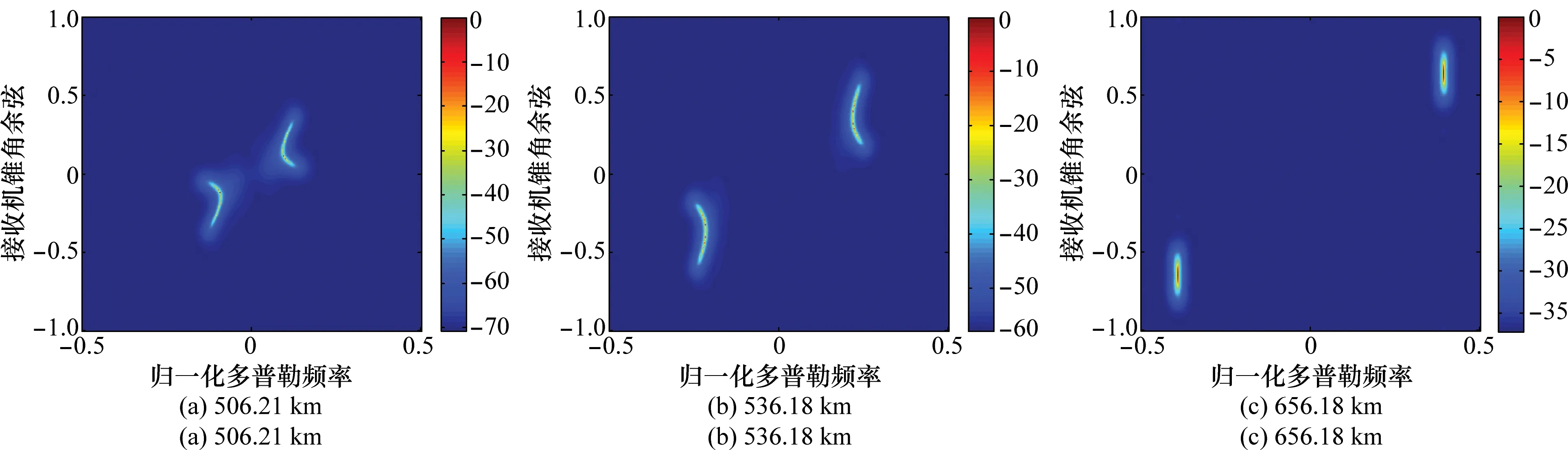
图8　平飞构型下不同距离杂波功率谱Fig.8　Space-time clutter spectrum of single range in parallel geometry

3.2发射机与接收机垂直飞行

在这种情况下,接收机垂直于基线飞行,发射机朝向接收机飞行。以基线为轴,接收机为原点,发射机与接收机速度相对轴向偏角分别为180°和90°。图9为杂波的空时分布关系,其中图9(a)为整个地面杂波的空时分布,图9(b)为有效散射区域杂波的空时分布。虽然图9(a)所示杂波的空时分布特性与第3.1节双基结构下图5(a)所示杂波的空时分布存在较大差异,但图9(b)所示有效散射区域杂波的空时分布特性与图5(b)所示杂波的空时分布具有很高的相似性:二者均为完整连续的空时谱线被条带截断的部分,被截断部分在每个距离都是孤立的两段谱线,其同时保留了整个地面杂波最大的距离依赖性。

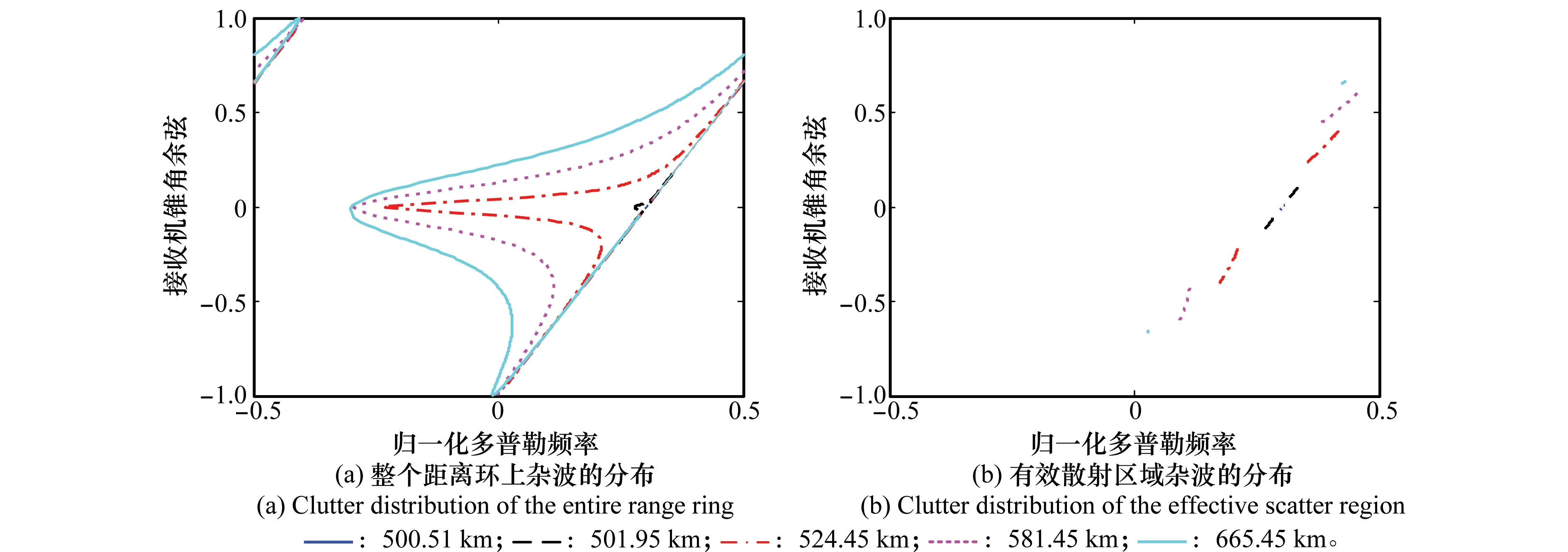
图9　垂直构型下不同距离杂波的空时分布Fig.9　Space-time clutter distribution of vertical geometry

下面对杂波的功率谱进行仿真分析,图10为实际杂波的距离多普勒功率谱,图11为536.18km距离处杂波的空时功率谱,功率谱的估计方法与第3.1节方法一致。相比图6所示杂波的距离多普勒功率谱,图10所示功率谱一方面展现出同样的频谱截断现象,在单一距离处分布为两段孤立的谱线,另一方面在频谱中心位置、频谱宽度等方面与图6略有差异。同样,相比图8(b)所示相同距离处杂波的空时功率谱,图11所示相同距离处杂波的空时功率谱一方面具有相同的条带式截断特性现象,另一方面杂波多普勒中心和轨迹形状与图8(b)略有差异。

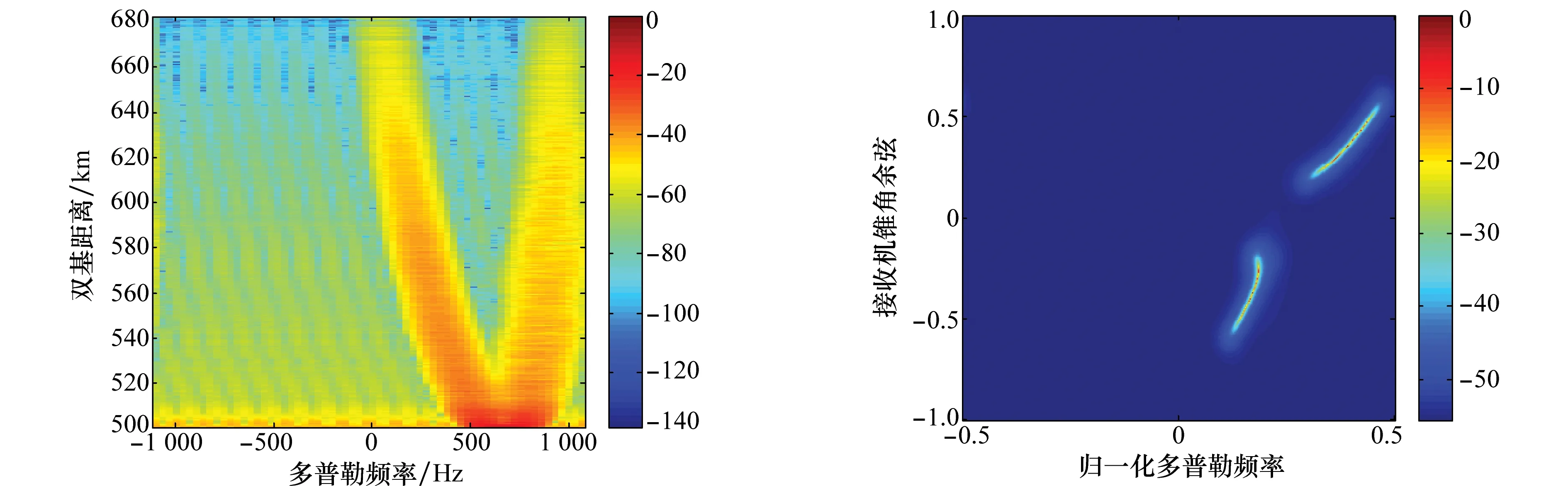
图10　垂直构型下的距离多普勒杂波谱　　　　　　　　　　　　图11　垂直构型下的空时杂波谱(536.18 km)　　　　　　　Fig.10　Range-Doppler spectrum of vertical geometry　　　Fig.11　Space-time clutter spectrum of vertical geometry (536.18 km)

相比第3.1节的仿真分析结果,不同双基构型对杂波分布的中心位置、分布范围和谱线形状有略微影响,但整体来看,杂波分布的主要特性维持不变,即杂波分布的条带式截断特性和显著的距离依赖性维持不变。

3.3发射机与接收机相交飞行

在这种双基构型下,发射机与接收机速度相对轴向偏角分别为45°和90°。同样,首先分析杂波的空时分布特性,之后仿真分析杂波的功率谱及其距离依赖性。图12(a)和图12 (b)分别为整个地面和有效散射区域杂波的空时耦合特性曲线。对比不同双基构型下整个地面杂波的空时分布情况,图12(a)所示杂波分布相比图5(a)所示杂波分布具有一定相似性,而与图7(a)所示杂波分布变化较大,因此整体来看不同双基构型会对杂波的空时分布产生较大影响。但在超长基线双基机载雷达情况下,通过对比不同双基构型下杂波的分布特性如图5(b)、图9(b)和图12(b)所示,3种情况下杂波的空时分布存在十分明显的共同特性,有效散射曲杂波具有条带式截断特性,且被截断部分保留了整个地面杂波距离依赖性最为显著的部分。

发射机与接收机相交飞行情况下,超长基线双基机载雷达杂波功率谱仿真结果如图13和图14所示。与第3.1节和第3.2节类似,图13和图14分别为杂波的距离多普勒功率谱和距离为536.18km处杂波的空时功率谱的估计结果。与上文的分析结果一致,杂波在距离多普勒域为孤立的两段谱线,且随距离变化显著,在空时频率域同样是连续杂波谱线被条带式截断的两段孤立谱线。相比第3.1节,杂波谱除过轻微形变和一定的中心偏移,整体上几乎保留了相同的分布特性。

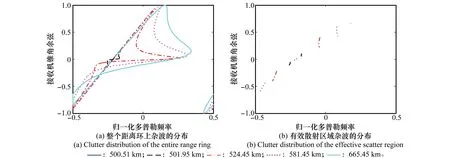
图12　交叉构型下杂波的空时分布Fig.12　Space-time clutter distribution of cross geometry

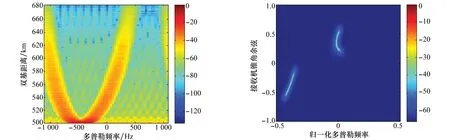
图13　交叉构型下的距离多普勒杂波谱　　　　　　　　　　　图14　交叉构型下的空时杂波谱(536.18 km)　　　　　　Fig.13　Range-Doppler spectrum of cross geometry　　　Fig.14　Space-time clutter spectrum of cross geometry (536.18 km)

3.4接收机偏航对杂波特性的影响

接收机载机在飞行过程中由于气流不稳定等因素的影响,飞行方向一般存在5°～10°的偏航,这会在接收阵列和载机航向间引入一个偏航角,这样的非正侧视结构一般会加重杂波统计特性的非平稳性。下面仿真分析接收机偏航对杂波特性的影响。考虑发射机和接收机平行飞行的双基构型,在接收阵列存在10°偏航的情况下,图15分析了不同距离杂波理论上的空时分布特性,其中图15(a)为整个地面杂波的空时分布,图15(b)为有效散射区域杂波的空时分布。相较图5(a),接收机偏航导致图15(a)所示杂波的空时分布特性发生较大变化:杂波中心发生偏移且轨迹形状发生变化。考虑有效散射区域的杂波散射,相较图5(b),图15(b)所示杂波的空时分布并未发生明显形变,但其沿空间频率方向发生一定频移,也就是说当偏航角不大时,接收机偏航会引入杂波的空间频率位移,但对有效散射区域杂波的分布形状影响较小。

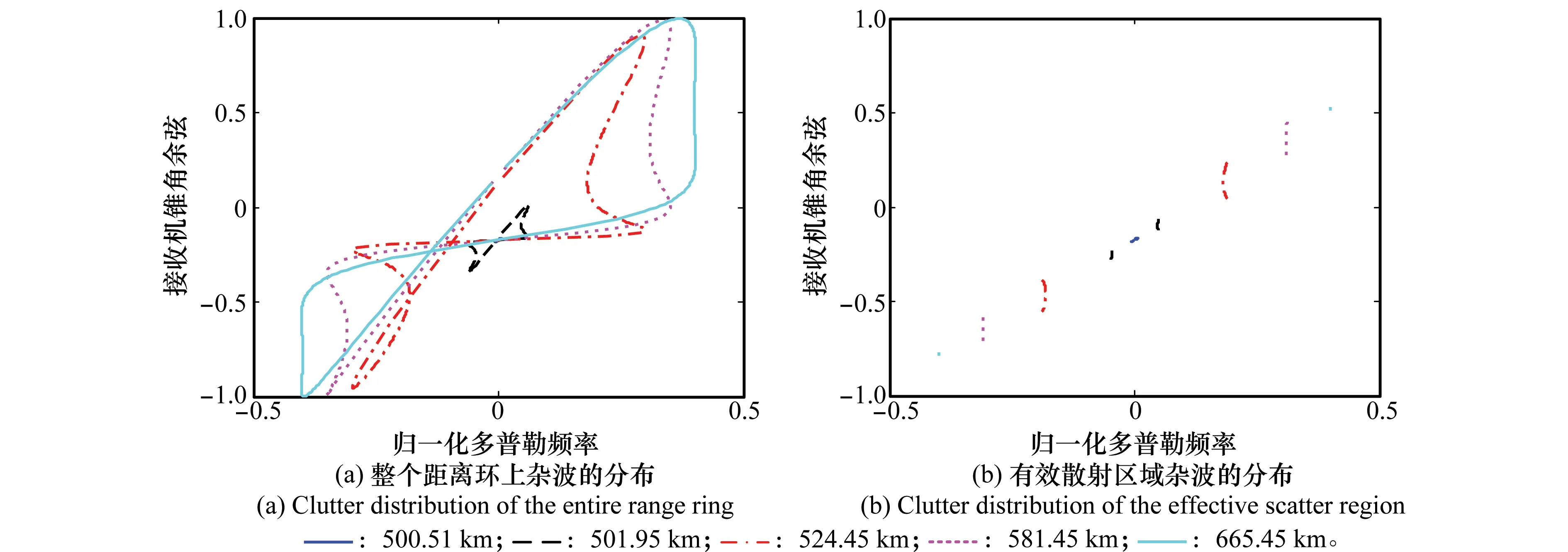
图15　接收机10°偏航下杂波的空时分布Fig.15　Space-time clutter distribution with 10° crab angle

在上述接收机偏航情况下,空时杂波谱仿真结果如图16和图17所示,其中图16为杂波的距离多普勒功率谱,图17为所有距离杂波的平均空时功率谱。图16所示距离多普勒功率谱与图6几乎完全一致,这是因为距离多普勒谱不包含空域信息,不受接收机阵列偏航影响。为了反映杂波空域分布特性,图17给出了所有距离处杂波的分布范围,对比图7可发现杂波分布条带仅发生空域平移及很轻微的弯曲,与图15(b)分析结果一致。通过计算单个距离环杂波的真实协方差矩阵,对其采用MVDR方法估计得到图18所示杂波的空时功率谱。由图18可见,其空时分布轨迹与图8所示杂波空时功率谱高度相似,但杂波谱发生空间频率生偏移。经过仿真验证,对于其他双基几何构型,接收机阵列偏航对杂波空时分布特性也具有相似的影响:虽然整个地面杂波的空时分布受偏航影响较大,但有效散射区域杂波空时分布基本保持不变,杂波条带有很轻微弯曲以及一定的空间频率偏移。

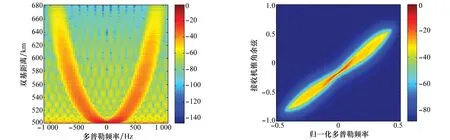
图16　接收机10°偏航下杂波的距离多普勒功率谱　　　　　　　图17　接收机10°偏航下所有距离平均的杂波功率谱　　　Fig.16　Range-Doppler clutter spectrum with 10° crab angle　　　　Fig.17　Average space-time clutter spectrum with 10° crab angle

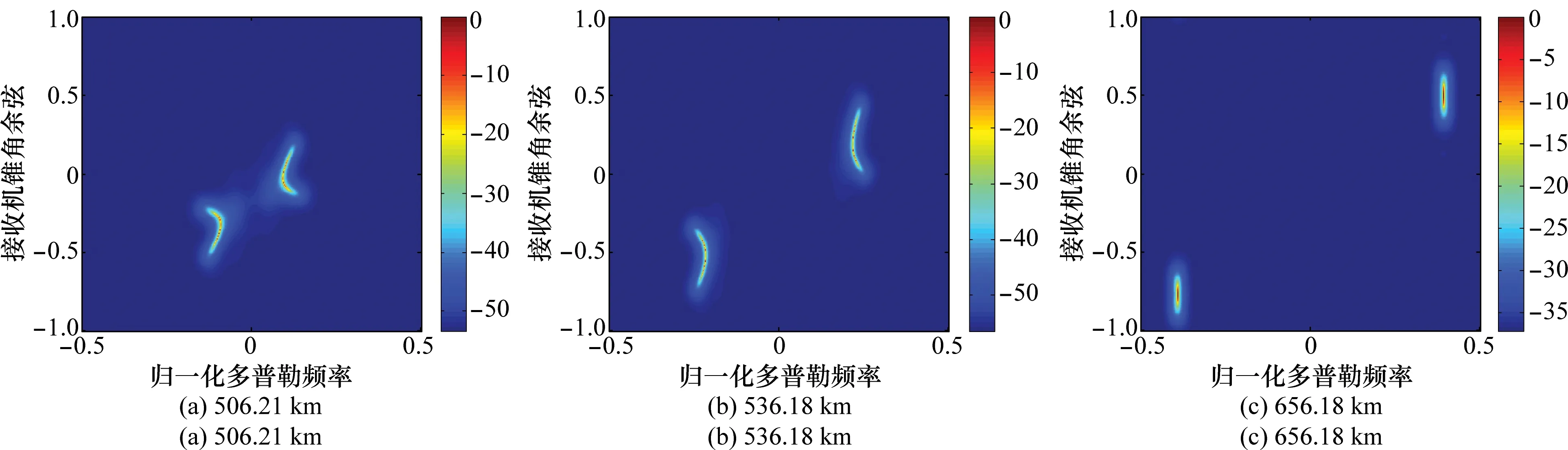
图18　接收机10°偏航下不同距离杂波功率谱Fig.18　Space-time clutter spectrum of single range with 10° crab angle

通过以上3种典型双基构型及接收机偏航影响下杂波特性的详细分析和对比,总结得出超长基线双基机载雷达杂波的一些重要特性:在不同双基构型下,有效散射区域杂波的空时分布具有条带式截断的共同特性,双基构型不会严重影响该区域杂波的整体分布特性;双基雷达构型主要影响单个距离处谱线的形状和多普勒中心的位置,而偏航主要改变单个距离处杂波空间频率的中心位置;在固定双基雷达构型下,接收机偏航角会改变有效散射区域杂波空间频率的中心位置,但对其空时分布轨迹形状影响较小。

4　结　论

本文充分考虑地球曲率对超长基线机载双基雷达构型和杂波特性的影响,建立了地心直角坐标系下的模型,推导了等距离环的解析表达式,得出双基雷达等距离环在基线-地心平面的投影是一条抛物线,并通过菲涅尔近似求得其定义域边界的近似解析解。通过分析杂波的空时耦合特性、距离多普勒功率谱和空时功率谱,研究了超长基线双基机载雷达杂波分布的条带式截断特性和距离依赖性:杂波的空时分布不再连续,而是两段孤立的谱线,被截断部分杂波的距离依赖性是整个地面最显著的部分。分析表明,超长基线双基机载雷达杂波的展宽程度较普通双基雷达小得多,但其距离依赖性依然十分显著,双基构型影响其谱线形状和多普勒中心,而接收机偏航主要影响其空间频率中心,但二者几乎不影响截断条带的形状。在后续设计STAP方法时需要充分考虑并结合杂波的条带式截断特性,减轻杂波距离依赖性对滤波器训练的影响,从而充分利用空时自由度进行有效的杂波抑制。

[1]WillisNJ,GriffithsHD. Advances in bistatic radar[M].USA:SciTechPublishingIncorporated, 2007: 432-433.

[2]ZhangYH,HimedB.Effectsofgeometryoncluttercharacteristicsofbistaticradars[C]∥Proc.of the IEEE Radar Conference, 2003: 417-424.

[3]KlemmR.ComparisonbetweenmonostaticandbistaticantennaconfigurationsforSTAP[J].IEEE Trans. on Aerospace and Electronic Systems, 2000, 36(2): 596-608.

[4]MelvinWL,DavisME.Adaptivecancellationmethodforgeometry-inducednonstationarybistaticclutterenvironments[J].IEEE Trans. on Aerospace and Electronic Systems,2007,43(2):651-672.

[5]HimedB.EffectsofbistaticclutterdispersiononSTAPsystems[C]∥Proc.of the IEEE National Radar Conference, 2002: 360-364.

[6]HimedB,ZhangYH,HajjariA.STAPwithangle-Dopplercompensationforbistaticairborneradars[C]∥Proc.of the IEEE National Radar Conference, 2002: 311-317.

[7]PearsonF,BorsariG.Simulationandanalysisofadaptiveinterferencesuppressionforbistaticsurveillanceradars[R].Lexington:AdaptiveSensorArrayProcessingWorkshopMITLincolnLab, 2001.

[8]ZatmanM.Performanceanalysisofthederivativebasedupdatingmethod[R].Lexington:AdaptiveSensorArrayProcessingWorkshop,MITLincolnLab, 2001.

[9]LapierreFD,VerlyJG.Registration-basedrangedependencecompensationforbistaticSTAPradar[J].EURASIP Journal of Applied Signal Processing, 2005(1): 85-98.

[10]HimedB,MichelsJH,ZhangYH.BistaticSTAPperformanceanalysisinradarapplications[C]∥Proc.of the IEEE Radar Conference, 2001: 198-203.

[11]WuH,WangYL.Modelingandanalysisofthegroundclutterspectrumonbistaticairborneearlywarningradar[J].Chinese Journal of Electronics,2006,34(12):2209-2213.(吴洪,王永良.双基地机载预警雷达杂波建模与分析[J].电子学报,2006,34(12):2209-2213.)

[12]MengX,WangT,WuJ,etal.Bistaticclutteranalysisandrangeambiguityresolvingforspacetimeadaptiveprocessing[J].IET Radar, Sonar and Navigation, 2009,3(5): 502-511.

[13]LiH,TangJ,PengYN.Modelingofspace-timeclutterforbistaticspacebasedradar[J].Chinese Journal of Electronics,2008,36(3):417-420.(李华,汤俊,彭应宁.星载双基地雷达空时二维杂波建模方法[J].电子学报,2008,36(3):417-420.)

Modeling and characteristics analysis of space-time clutter for ultralong baseline bistatic airborne radar

WANG Cheng-hao1,2, LIAO Gui-sheng1,2, XU Jing-wei1,2, ZENG Cao1,2

(1. National Lab of Radar Signal Processing, Xidian University, Xi’an 710071, China;2.CollaborativeInnovationCenterofInformationSensingandUnderstanding,Xi’an710071,China)

Under the effect of earth curvature on geometry of ultralong baseline bistatic airborne radar, the space-time clutter distribution severely depends on bistatic geometry and area of beam coverage. To solve this problem, analytical expression of the iso-range ring is derived in geocentric coordinates and it turns out that the projection of the iso-range ring on plumb surface in which the baseline lies is parabolic. On analysis of several typical bistatic geometries and area of beam coverage, the stripped truncation characteristics of space-time distribution of clutter for ultralong baseline bistatic airborne radar and range-dependence of clutter are researched. Simulation results verify the validity and effectiveness of the conclusion.

ultralong baseline; bistatic airborne radar; space-time clutter; clutter modeling; clutter characteristics

2015-09-28；

2016-03-02；网络优先出版日期：2016-07-03。

国家自然科学基金(61231017, 61601339)资助课题

TN 957.52

A

10.3969/j.issn.1001-506X.2016.10.06

王成浩(1991-),男,博士研究生,主要研究方向为空时自适应处理。

E-mail:wangchenghao1991@126.com

廖桂生(1963-),男,教授,博士,主要研究方向为雷达探测系统空时自适应处理、天基预警和阵列信号处理。

E-mail:gsliao@xidian.edu.cn

许京伟(1987-),男,讲师,博士,主要研究方向为空时二维信号处理、稳健波束形成。

E-mail:xujingwei1987@163.com

曾操(1979-),男,副教授,博士,主要研究方向为阵列信号处、雷达地面动目标检测。

E-mail:czeng@mail.xidian.edu.cn

网络优先出版地址：http://www.cnki.net/kcms/detail/11.2422.TN.20160703.1241.006.html