一种适用于红外制导弹药的偏置比例导引律
王广帅, 林德福, 范世鹏, 臧路尧
(1. 北京理工大学宇航学院, 北京 100081; 2. 北京航天自动控制研究所, 北京 100854)
一种适用于红外制导弹药的偏置比例导引律
王广帅1, 林德福1, 范世鹏2, 臧路尧1
(1. 北京理工大学宇航学院, 北京 100081; 2. 北京航天自动控制研究所, 北京 100854)
针对弹道成型制导律不适用于红外制导弹药的落角约束,提出了一种无需剩余飞行时间信息的偏置比例导引律。根据建立的弹目相对运动几何模型和碰撞三角形,推导出了期望落角与需用偏置积分量之间的函数关系;求出了偏置比例导引无量纲弹道闭环解与稳定域,并分析了不同因素对偏置比例导引律制导性能的影响;最后对比研究了偏置比例导引制导律与弹道成型的性能。仿真结果表明,偏置比例导引律在落角精度、制导精度与最大需用过载这些关键制导性能指标方面接近于弹道成型制导律,适用于红外制导弹药对地面运动装甲目标的落角约束问题。
弹道成型制导律; 红外制导弹药; 偏置比例导引律; 落角约束
0 引 言
红外成像制导由于其灵敏度高、具备多目标鉴别能力和抗干扰能力强等特性,成为新一代反坦克导弹的一种主要制导方式[1-2]。例如,欧洲“崔格特”和美国“标枪”反坦克导弹均采用红外凝视成像制导技术,具有“发射后不用管”能力[3]。为提高对运动装甲目标的毁伤概率,红外反坦克导弹多采用掠飞攻顶方式来打击坦克装甲最薄弱的顶部,这就要求制导律在保证目标命中的基础上,同时实现落角约束[4]。
工程中增大落角最直接的方式就是在制导律中加入过重力补偿,文献[5]采用了带过重力补偿的比例导引来增大落角。但由于重力补偿系数与落角之间不存在直接对应的函数关系,因此难以实现对落角大小的精确控制。
国内外关于落角约束制导律的理论研究较多。最有代表性的是基于落角约束的最优制导律,实现落角约束的同时使得控制能量需求最小。文献[6]以“导弹过载平方的积分”为目标函数,从最优控制理论出发推导出了最优制导律,文献[7-9]以此为基础研究了相关扩展形式的最优制导律;以Zarchan为代表的学者从数学上Schwartz不等式出发,采用相同的目标函数推导出了相同形式的最优制导律—弹道成型[10-11]。国内学者将目标函数扩展为包含有剩余飞行时间幂函数,推导出末端过载为零的扩展弹道成型制导律,并对其性能进行了全面研究[13-15]。另外,在传统比例导引基础上加时变偏置项构成偏置比例导引律也是一种实现落角约束的方法,文献[15]加了一个与剩余飞行时间成函数关系的偏置项来构成偏置比例导引律,并且推导出了它的最优形式。
上述这些最优制导律实现落角精确控制的过程中均离不开当前剩余飞行时间信息,剩余飞行时间根据当前弹目距离来计算获得。由于红外导引头不像雷达导引头那样可以直接测量弹目距离,而只能通过在弹体上额外增加惯导组件或GPS制导模块来间接计算弹目距离,因此红外制导弹药采用最优制导律时就产生了额外的硬件需求问题。
本文在文献[16-17]提出的一种无需剩余飞行时间偏置比例导引律的基础上,进一步研究了这种制导律的无量纲解析解和稳定域,并将其应用于红外制导武器对地面慢速运动目标的落角约束中,在实现落角精确控制的同时避免了红外制导弹约的硬件额外需求问题。通过仿真,将这种偏置比例导引律与弹道成型制导律的制导性能进行了对比研究。
1 弹目相对运动模型
红外制导弹药打击地面慢速运动目标时弹目相对运动可分解为俯仰和偏航两个平面上的运动,鉴于二者没有本质区别,只研究俯仰平面的相对运动,几何关系如图1所示。

图1 弹目相对运动几何关系图Fig.1 Relative motion geometry between missile and target
图1中,M和T分别表示导弹与目标位置;R表示弹目距离;vt表示目标速度矢量;vm、ε、θ分别表示导弹的速度矢量、目标视角和速度倾角;vR、εR、θR分别表示相对速度的矢量、方向角和倾角。假设逆时针方向作为角度的正方向,则弹目相对运动微分方程组可表示为
(1)
弹道终端的弹体速度矢量vm,f、目标速度矢量vt和相对速度矢量vR,f组成了弹目碰撞三角形,如图2所示。um,f、ut、uR,f分别表示上述3个速度的单位矢量;θf、θR,f、Δθ分别表示碰撞时刻弹体终端落角、弹目相对速度倾角和弹体速度矢量与相对速度矢量间的夹角。
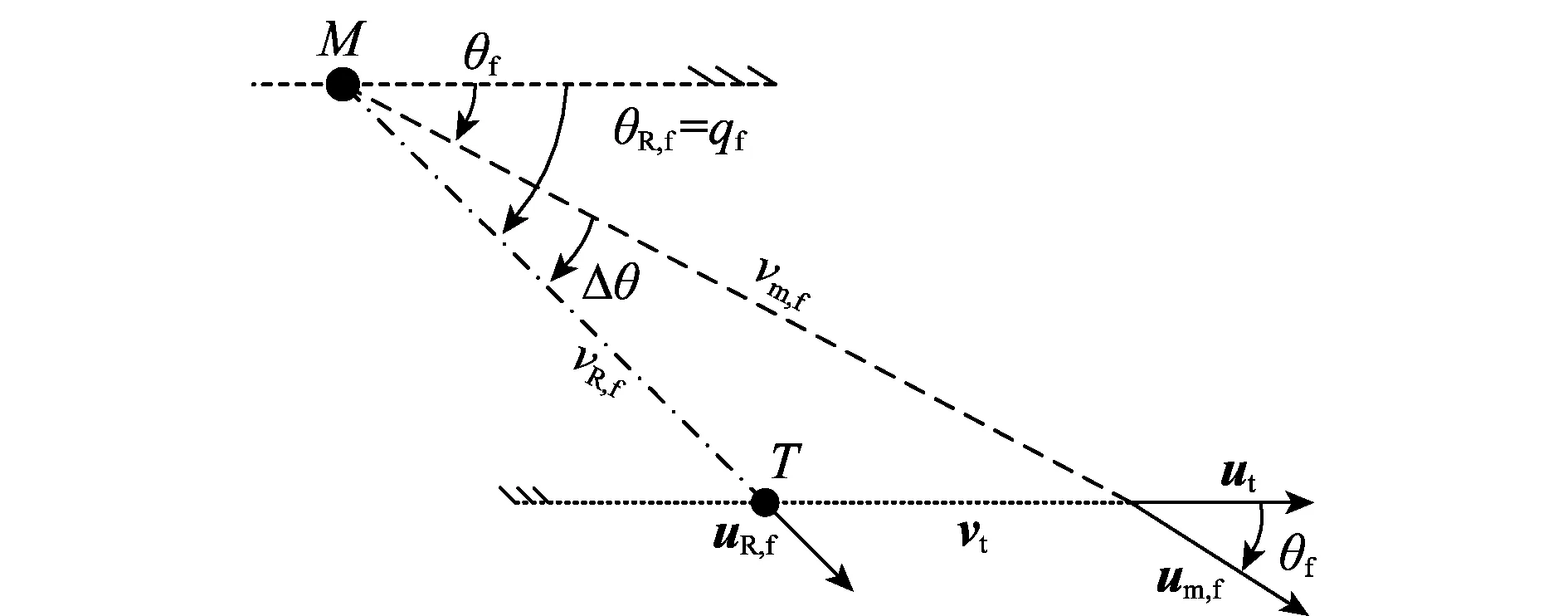
图2 弹目碰撞三角形Fig.2 Collision triangle between missile and target
分析碰撞三角形可得
(2)
根据三角形正弦定理得到速度夹角
(3)
导弹速度远大于目标速度,使得弹体速度与相对速度夹角为小量,故有
(4)
式(4)代入式(2)得到
(5)
考虑到弹体过载沿弹体速度法向,忽略重力和阻力,弹体速度vm是常值;相对速度vR是变量,采用余弦定理得到弹道终端相对速度:
(6)
式中,vt,f为弹道末端目标速度。令目标速度与导弹速度之比为
(7)
式(6)、式(7)代入式(5)得
(8)
同理,可得到初始时刻速度夹角为
(9)
由于k为小量,且其数值大小对相对速度倾角的计算影响较小,所以工程中可对k取常值,并根据目标类型提前装订;弹体初始速度倾角θi则可由载机外部传输或地面初始对准获取。
2 落角约束下的偏置比例导引律
2.1落角约束下比例导引的局限性
比例导引制导律可表示为
(10)
式(10)两边积分得
(11)
比例导引打击地面慢速移动目标时,弹道终端过载接近于零,碰撞前的某一微小时间段内终端弹体速度矢量和终端弹目相对速度矢量基本保持不变,因此弹道终端的弹目相对速度与弹目连线重合,即有
(12)
将式(1)和式(12)代入式(10)中,得
(13)
由于红外制导弹药弹体速度远大于地面目标速度,可知Δθ为小量,有
(14)
弹体的终端落角θf取决于有效导航比N、初始弹目视线角qi和初始相对速度方向角εR,i。有效导航比一般取值为3≤N≤5,因此比例导引制导律的落角范围
(15)
理论上比例导引可以实现大落角,而真实情况中制导初始时刻的弹目视线角与相对速度方向角限制了比例导引制导律落角的范围。
2.2弹道成型最优制导律
Zarchan利用Schwartz不等式推导出了弹道成型最优制导律[10],使得控制能量需求最小的同时,实现了落点与落角的双重约束,并成功应用于Apollo飞船登月等一系列重大工程项目,弹道成型制导律形式为
(16)
式中,tgo表示剩余飞行时间;qt表示当前弹目视线角;Γ表示期望落角。由于执行过程需要剩余飞行时间信息,从而产生了对额外的硬件需求问题,增加了弹体的复杂性,提高了生产成本。
2.3偏置比例导引制导律
弹道成型可以实现落角控制的根本原因是在其比例导引基础上复合了与剩余飞行时间和期望落角相关的偏置项。基于上述思想,通过在等式(8)右端加偏置项构成偏置比例导引律[13]:
(17)
式中,b表示偏置项。导引律两边积分得
(18)
由于偏置比例导引末端过载接近于零,同样弹道末端弹目相对速度与弹目连线重合,式(12)代入式(18)可得到期望落角Γ与需用偏置积分量BN之间的函数关系:
(19)
偏置比例导引律通过偏置项积分量B来实现对落角的精确控制。整个弹道飞行过程中,只要保证偏置项积分量B达到需用偏置积分量BN,终端落角为即为期望落角Γ。其中,初始弹目视线角qi可由载机或者地面装订;终端相对速度倾角Γ+Δθ与初始相对速度倾角θR,i可分别由式(7)、式(8)计算获得。
考虑到真实过载方向只能沿弹体速度法向,因此偏置比例导引律的过载指令为
(20)
由于相对速度与弹体速度夹角很小,为便于工程应用,将式(7)代入式(20)中,得到
(21)
3 弹道稳定性分析与偏置项分配
3.1弹道的闭环解
将偏置比例导引律引入到弹目相对运动数学模型中,获得偏置比例导引律的弹道非线性模型
(22)
对方程组无量纲化,令ρ=|b|R/vR,dτ=|b|dt,可得到
(23)
式中,σ表示偏置项b的符号,方程组平衡点坐标为{ρe,εe}={σ(N-1),π/2}。式(23)中的两个子式相除,得到
(24)
为使得弹体末端过载收敛,有效导航比取N>2。解微分方程得到有效导航比N>2时的无量纲弹道闭环通解:
(25)
式中,c为积分常数,其值取决于无量纲距离初值ρ0和相对速度方向角εR0。积分常数在平衡点处的值为
(26)
3.2弹道的稳定域
弹道的稳定性可通过相平面轨迹图中无量纲距离的收敛性来判断。为了满足工程中增大落角的需求,主要研究偏置项大于零的情况,此时σ=1,同时令导航比N=4,从而得到关于无量纲距离ρ和相对速度方向角εR的相平面轨迹图,如图3所示。图中每条相平面轨迹上的标识数字为其对应的积分常数c,实心圆点表示平衡点,其坐标为(ρe,εe)=(3,π/2),对应积分常数ce=-1/54。图中的轨迹簇被平衡点分为A、B、C和D共4组,每条箭头指向表示对应组曲线随时间变化的收敛方向。其中A、C两组轨迹无量纲距离收敛到零,表明其弹道稳定收敛到目标;而B、D两组曲线是发散的。

图3 相平面轨迹(N=4)Fig.3 State plane trajectories (N=4)
可见,弹道稳定性取决于积分常数c和初值ρ0,稳定域为:{c
在已知初始条件ρ0和ε0的情况下,弹道稳定的判断策略如图4所示。当c>ce,ρ0>ρe或c 图4 初始条件下弹道稳定性判定策略图Fig.4 Diagram of judgement strategy for trajectory stability under certain initial conditions 3.3偏置比例导引偏置项分配 由于不能事先准确获得整个弹道飞行时间信息,为保证偏置积分量B达到需用偏置积分量BN,应使得偏置持续时间H小于真实弹道飞行时间。同时,为保证稳定性分析有效,应使得当前偏置项大小与相对速度vR成正比。 (27) 此时,初始偏置量b0取为 (28) 当前偏置项根据初始偏置项来计算得出 (29) 尽管偏置持续时间计算不准确,但考虑真实弹道较弯 曲且导弹速度基本不变,所以仍然可以保证偏置持续时间小于弹道真实飞行时间。 整个弹道由偏置比例导引段和比例导引段组成。偏置比例导引段完成需用偏置积分量后,切换至比例导引,然后由比例导引最终实现落角与落点的精度控制。 根据前面相平面轨迹分析可知,对于比例导引制导段,在切换点处必定存在一定初始相对速度方向误差角εRM,当此段飞行时间不足以消除相对速度方向误差的影响时,将会影响到整个弹道的落角精度与制导精度。 4.1偏置比例导引律制导性能研究 为研究期望落角Γ、偏置起始时间t1、偏置持续时间H和有效导航比N对偏置比例导引律制导性能的影响,仿真条件设为6个场景,仿真所得需用偏置积分量、起始偏置、实际终端落角、脱靶量和控制能量需求如表1所示,其中偏置持续时间H的变化通过调整初始偏置项大小来间接实现。仿真所得偏置项、纵向平面弹道、指令过载、目标视角和控制能量需求曲线如图5~图9所示。 表1 偏置比例导引性能研究仿真场景设置 图5 偏置比例导引偏置项曲线Fig.5 Bias profile of biased PNG 图7 偏置比例导引指令过载曲线Fig.7 Command acceleration histories of biased PNG 对比场景1、场景2和场景3可知,增大期望落角Γ,需用偏置积分量、初始偏置增大;并且飞行过程中的最大需用过载、控制能量需求和目视视角都会增大;当存在过载与目标视角限制时,期望落角并不是越大越好。由于落角增大使得比例导引段飞行时间加长,导致初始相对速度方向误差εRM的影响减小,使得整个弹道终端落角与制导精度明显提高。 图8 偏置比例导引目标视角曲线Fig.8 Look angle variations of biased PNG 图9 偏置比例导引能量消耗曲线Fig.9 Control effort curve of biased PNG 对比场景2与场景4,偏置起始时间t1后移可有效降低弹道高度并缩短飞行时间,但增大了最大需用过载与控制能量需求。由于起始比例导引段飞行时间缩短,并且导引头进入盲区时保持过载与实际过载需求偏差增大,导致落角精度与制导精度有所降低。 对比场景2与场景5,适度减小偏置持续时间H,可明显提高落角与制导精度并有效降低最大需用过载。原因在于H的减小增大了比例导引段飞行时间,同时使得切换时刻弹目距离增大,从而减小了切换时刻弹目视线角速度。而当偏置持续时间H过小时,意味着偏置项过大,将使偏置比例导引段弹道失稳,目标视角的急剧增大,使得目标易出视场,如图8所示。 对比场景2与场景6,有效导航比N增大,需用偏置积分量BN增大,从而使得偏置项增大,最大需用过载与控制能量需求提高;同时更长比例导引飞行时间与盲区更小的过载保持大大提高了落角与制导精度。 综合对比分析,适度减小偏置持续时间可以作为提高落角与制导精度的同时又能降低最大过载的一种有效手段。 4.2与弹道成型最优制导律的对比研究 为对比偏置比例导引与弹道成型最优制导律的性能,共设定6个仿真场景,具体参数设置及相应的落角精度、制导精度与最大需用过载如表2所示。两种制导律的纵向弹道、过载、目标视角和控制能量需求曲线分别如图10~图13所示。 两种制导律均能在命中运动目标的情况下准确实现落角约束;偏置比例导引落角和制导精度低于弹道成型。减小偏置持续时间可以增大比例导引段飞行时间,有效提高偏置比例导引的落角与制导精度,使其接近于弹道成型落角与制导精度,如表2所示。 表2 两种制导律对比研究仿真场景设置 偏置比例导引的弹道高度大于弹道成型,弹道更加弯曲,使得其飞行时间大于弹道成型飞行时间,如图10所示。 图10 两种制导律的纵向弹道对比Fig.10 Spatial trajectories comparison between biased PNG and trajectory shaping guidance 对于弹道末段过载的需求,偏置比例导引逐渐减小,而弹道成型则单调增大;前者最大需用过载出现在弹道中段,后者则出现在弹道末端;尽管偏置比例导引最大需用过载大于弹道成型,鉴于实际情况末制导段速度逐渐减小,偏置比例导引并不比弹道成型更容易出现过载饱和现象。同样可通过减小偏置持续时间使其大落角下的最大需用过载接近于弹道成型最大需用过载,如图11所示。 图11 两种制导律的纵向过载对比Fig.11 Command acceleration comparison between biased PNG and trajectory shaping guidance 采用偏置比例导引制导过程中,其目标视角大于弹道成型的目标视角,且二者差距随着期望落角或偏置项的增大而增大,如图12所示。 图12 两种制导律的目标视角对比Fig.12 Look angle comparison between biased PNG and trajectory shaping guidance 偏置比例导引的控制能量需求大于弹道成型,这是由于弹道成型是基于控制能量最优推导出的最优制导律;且偏置项越小,二者越接近,如图13所示。 综合分析可得,偏置比例导引律的落角与制导精度低于弹道成型,最大需用过载大于弹道成型最大需用过载。保证目标视角满足导引头视场域约束并且满足弹道稳定性的前提下,尽量减小偏置持续时间可以使其落角与制导精度接近弹道成型的同时,保证大落角约束下的最大过载接近于弹道成型最大过载。 图13 两种制导律的能量消耗对比Fig.13 Control effort comparison between biased PNG and trajectory shaping guidance 本文采用的偏置比例导引律本质上是偏置比例导引加比例导引的组合制导律,偏置比例导引可视作为比例导引的中制导,负责将导弹导引至满足比例导引实现期望落角所需的特定初始条件,然后由比例导引最终实现落点与落角的约束,其中比例导引段飞行时间影响着落角与制导精度。 研究表明:适度减小偏置持续时间可以提高落角与制导精度的同时又能降低最大过载;通过合理设计偏置持续时间,可使得偏置比例导引律在落角精度、制导精度与最大需用过载这些关键的制导性能方面接近于弹道成型制导律。同时,其相对于弹道成型制导律的最大优势在于偏置比例导引律无需剩余飞行时间信息,更适用于打击地面运动装甲目标的红外成像制导弹药。 [1]XuLJ,ChenHX.Improvementofinfraredhorizondetectorusingtwo-dimensionalinfraredtemperaturedistributionmodel[C]∥Proc.of the AIAA Guidance, Navigation, and Control Conference, 2015: 335-347. [2]MainiAK,VermaAL,AgrawalV.Targetsimulatorforserviceabilitycheckofinfrared-guidedmissiles[J].Journal of Spacecraft and Rockets, 2011, 48(1): 175-181. [3]SonawaneHR,MahulikarSP.Effectofmissileturnrateonaircraftsusceptibilitytoinfrared-guidedmissile[J].Journal of Aircraft, 2013, 50(2): 663-667. [4]RatnooA,GhoseD.Impactangleconstrainedguidanceagainstnonstationarynonmaneuveringtargets[J].Journal of Guidance, Control, and Dynamics, 2010, 33(1):269-275. [5]LinDF,QiZK,XiaQL.Designandidentificationonparametersofproportationnavigationguidancelawwithgravityovercompensation[J].Journal of System Simulation, 2006, 18(10):2753-2756.(林德福,祁载康,夏群力. 带过重力补偿的比例导引制导律参数辨识与设计[J].系统仿真学报,2006,18(10):2753-2756.) [6]KimM,GriderKV.Terminalguidanceforimpactattitudeangleconstrainedflighttrajectories[J].IEEE Trans. on Aerospace and Electronic Systems, 1973, 9(6): 852-859. [7]ChoHQ,RyooCK,TsourdosA,etal.Optimalimpactanglecontrolguidancelawbasedonlinearizationaboutcollisiontriangle[J].Journal of Guidance, Control, and Dynamics, 2014, 37(3): 958-964. [8]LeeCH,KimTH,TahkMJ,etal.Polynomialguidancelawsconsideringterminalimpactangleandaccelerationconstraints[J].IEEE Trans.on Aerospace and Electronic Systems, 2013, 49(1): 74-92. [9]ParkBG,KimTH,TahkMJ.Optimalimpactanglecontrolguidancelawconsideringtheseeker’sfield-of-viewlimits[J].Journal of Aerospace Engineering, 2013, 227(8): 1347-1364. [10]PaulZ. Tactical and strategic missile guidance[M]. 6thed.Lexington:ProgressinAstronauticsandAeronautics, 2012: 569-601. [11]RatnooA,HayounS,GranotA,etal.Pathfollowingusingtrajectoryshapingguidance[C]∥Proc.of the AIAA Guidance, Navigation, and Control Conference, 2013: 5233-5255. [12]WangH,LinDF,WangJ,etal.Analysisandapplicationstudyontheextendedtrajectoryshapingguidancelaw[J].Acta Armamentarii, 2013, 34(7): 801-809. (王辉,林德福,王江,等. 扩展弹道成型末制导律特性分析与应用研究[J].兵工学报, 2013, 34(7): 801-809.) [13]WangH,LinDF,CuiXX.Extendedtrajectoryshapingguidancelaws[J].Transactions of Beijing Institute of Technology, 2014, 34(6): 597-602. (王辉,林德福,崔晓曦. 一类扩展弹道成型制导律[J].北京理工大学学报, 2014, 34(6): 597-602.) [14]WangH,WangJ,LinDF,etal.Analyticstudyonextendedtrajectoryshapingguidancesystemwithfirst-orderautopilotdynamics[J].Systems Engineering and Electronics, 2014, 36(3): 509-518.(王辉,王江,林德福,等.考虑一阶驾驶仪动力学的扩展弹道成型制导系统解析研究[J].系统工程与电子技术,2014,36(3): 509-518.) [15]KimBS,LeeJG,HanHS.BiasedPNGlawforimpactwithangularconstraint[J].IEEE Trans. on Aerospace and Electronic Systems, 1998, 34(1): 277-288. [16]LeeCH,KimTH,TahkMJ.BiasedPNGfortargetobservabilityenhancementagainstnonmaneuveringtargets[J].IEEE Trans. on Aerospace and Electronic Systems, 2015, 51(1): 55-72. [17]KoraySE.IndirectcontrolofimpactangleagainststationarytargetsusingbiasedPPN[C]∥Proc.of the AIAA Guidance, Navigation, and Control Conference, 2010: 8148-8154. [18]KoraySE,OsmanM.Indirectimpactanglecontrolagainststationarytargetsusingbiasedpreproportionalnavigation[J].Journal of Guidance, Control and Dynamics, 2012, 35(2): 700-703. [19]KoraySE.Controlofimpactangleusingbiasedproportionalnavigation[C]∥Proc.of the AIAA Guidance, Navigation, and Control Conference, 2013: 5113-5127. [20]TekinR,KoraySE.Switched-gainguidanceforimpactanglecontrolunderphysicalconstraints[J].Journal of Guidance, Control, and Dynamics, 2015,38(2):205-216. Biased proportional navigation applicable for infrared guidance munitions WANG Guang-shuai1, LIN De-fu1, FAN Shi-peng2, ZANG Lu-yao1 (1. School of Aerospace Engineering, Beijing Institute of Technology, Beijing 100081, China;2.BeijingAerospaceAutomaticControlInstitute,Beijing100854,China) Considering trajectory shaping guidance is unavailable for the constraint of the impact angle of infrared guidance munitions which could not supply time-to-go information, a kind of biased proportional navigation guidance, without time-to-go for its input, is proposed. Based on the established munitions-target relative motion model and collision triangle, the relationship between the desired impact angle and the demand bias integral quantity is derived. Then, the differential equation of engagement kinematics is solved and the stable region is obtained. The influence of some relevant factor on guidance performance of the proposed guidance is studied. The biased proportional guidance performance is also compared with that of the trajectory shaping guidance. Simulation results show that the biased proportional navigation is competitive with the trajectory shaping guidance in the key performance indexes, such as impact angle control precision, guidance and control precision and the maximum demand acceleration and that it could be used for the constraint of impact angle of infrared guided munitions. trajectory shaping guidance; infrared guidance munitions; biased proportional navigation; constraint of impact angle 2015-07-30; 2015-12-15;网络优先出版日期:2016-06-02。 国家自然科学基金(61172182)资助课题 TJ 765.2 A 10.3969/j.issn.1001-506X.2016.10.18 王广帅(1987-),男,博士研究生,主要研究方向为飞行器制导与控制。 E-mail:wangguangshuai88@sina.com林德福(1971-),男,教授,博士,主要研究方向为飞行器制导与控制。 E-mail:lindf@bit.edu.cn范世鹏(1986-),男,博士,主要研究方向为飞行器制导与控制。 E-mail:fspzxm@sina.com臧路尧(1987-),男,博士研究生,主要研究方向为飞行器制导与控制。 E-mail:luyao_jizi@126.com 网络优先出版地址:http://www.cnki.net/kcms/detail/11.2422.TN.20160602.1526.004.html

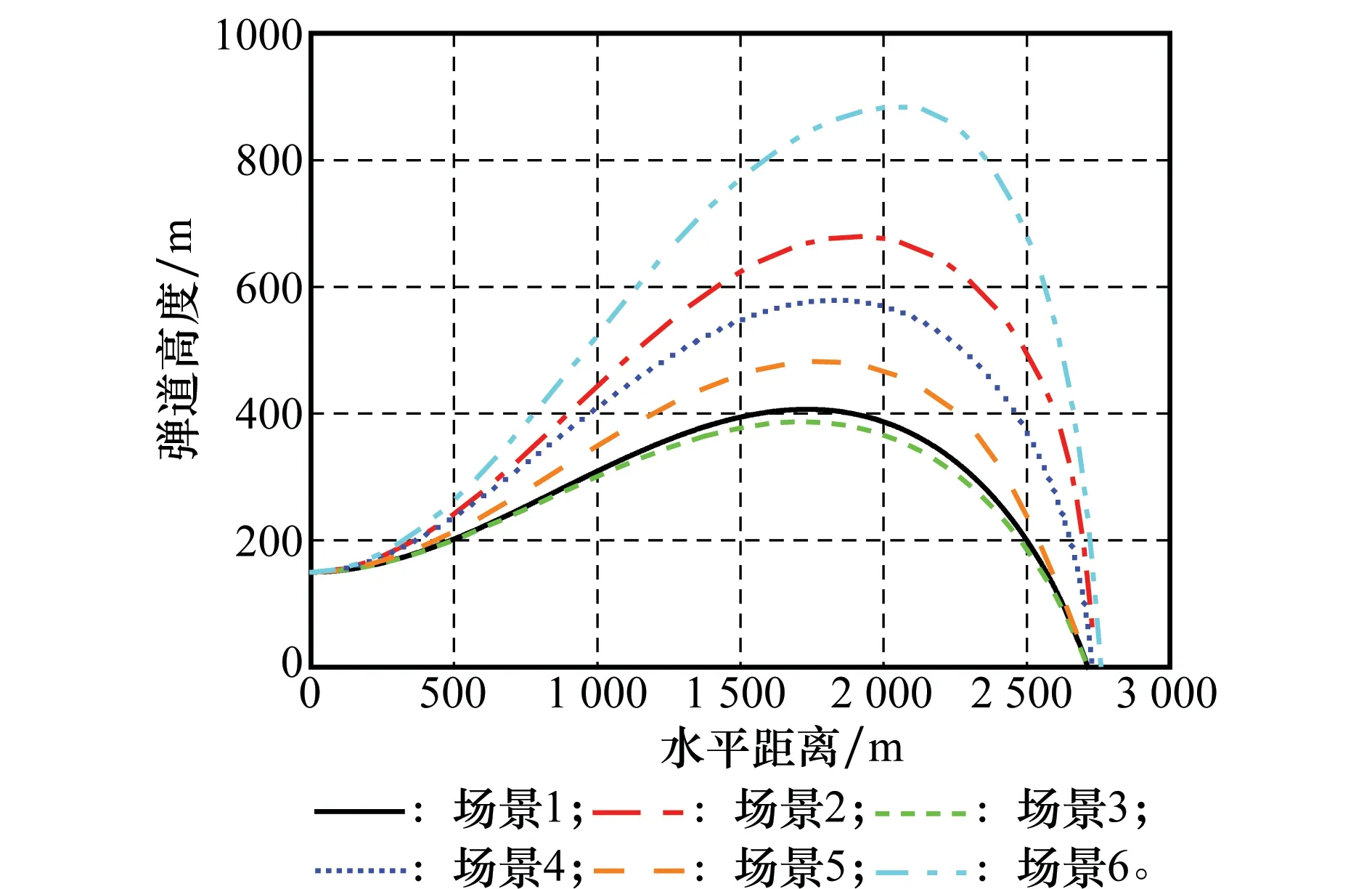
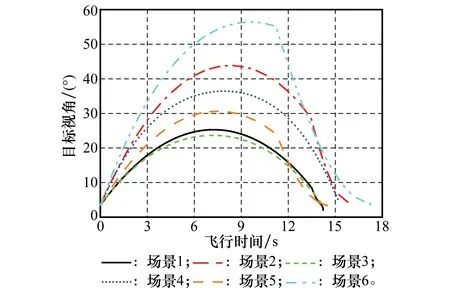
4 仿真分析









5 结 论

