基于大衍数列的规则QC-LDPC码构造方法
黄 胜,穆 攀,张 睿,袁建国
(重庆邮电大学 光通信与网络重点实验室,重庆 400065)
基于大衍数列的规则QC-LDPC码构造方法
黄胜,穆攀,张睿,袁建国
(重庆邮电大学 光通信与网络重点实验室,重庆 400065)
结合杨辉三角的结构形式,基于大衍数列提出了一种列重为3或4的规则准循环低密度奇偶校验(QC-LDPC)码的新构造方法。该方法构造的校验矩阵围长至少为6,码长可灵活变化,并且可节省存储空间。仿真结果表明: 在相同的仿真参数下,当误码率(BER)为10-6时,所构造的列重为3的QC-LDPC(1260,620)码的净编码增益(NCG)比二次函数码改善了1 dB左右;列重为4的QC-LDPC(6056, 3028)码相对于WMC-OCS、QC-OCS码分别有0.1 dB和0.2 dB的NCG提升。
规则QC-LDPC码; 杨辉三角; 大衍数列
低密度奇偶校验码(LDPC)是一类性能接近香农限、纠错能力强的线性分组码,自从它被重新发现以来,LDPC码的设计、构造、分析、编译码器的实现以及在数字通信系统中的应用都已经成为了人们研究的焦点,成为Turbo码的有力竞争者。LDPC码的构造方法根据校验矩阵的结构特点可分为两种:随机构造和代数构造。随机构造法有Gallager构造[1]、Mackay构造[2]、Hu等人为尽可能增大围长提出的经典PEG算法[3]等。这些基于计算机搜索构造出的码字参数选择灵活,性能优异。但是,随机构造所产生的校验矩阵没有固定的结构,导致编码复杂度高、存储困难、硬件难以实现。为了克服随机构造的这些缺点,代数的思想被纳入到LDPC码的构造中,人们提出了基于有限域[4]、有限几何[5]、组合数学[6]等构造法,这些方法构造的码字具有比随机码更低的编码复杂度,尤其是具有循环或准循环特性的LDPC码,已被广泛应用于通信系统中。
近些年来,人们提出了许多基于组合数学构造LDPC码的设计方案,比较典型的是BIBD构造法[7],此外,还有很多利用差集、数列等构造LDPC码的方法[8-9]。根据大衍数列固定项差对应的值单调递增的性质,朱磊基提出了一种基于大衍数列构造LDPC码的方法[10],方法简单,所构造的校验矩阵具有准循环结构,长码长的QC-LDPC码具有优异的性能,但此方法只限于构造优异的长码字。相对于长码而言,中短码的编译复杂度低,被广泛地应用于高速率无线通信及数据存储通信等领域,因此对中短码长的研究具有极好的理论和实践意义。本文结合杨辉三角的构造形式,基于大衍数列提出了一种适宜于构造中短码长的列重为3或4的规则QC-LDPC码的新方法(简称为DY-QC-LDPC码)。
1 融合大衍数列和杨辉三角的QC-LDPC码构造
行重为L、列重为J、码长N=P×L的(J,L)QC-LDPC的校验矩阵可以表示为
(1)
式中:IPj,l为循环置换矩阵;Pj,l表示P×P的单位矩阵右移移位次数;Pj,l取值范围为{0,1,…,P-1}或者∞,Pj,l=0时表示IPj,l为单位矩阵,Pj,l=∞时表示IPj,l为全零矩阵。
将校验矩阵H中的循环置换矩阵用循环移位次数Pj,l表示,得到参数移位次数Pj,l构成的基矩阵P,为
(2)
当基础矩阵确定后,QC-LDPC码的校验矩阵也就唯一确定了。校验矩阵H中长度为2k的环可以由基矩阵P中长为2k的序列(Pj1,l1,Pj1,l2,Pj2,l1,…,Pjk,lk,Pjk,l1)表示,对于由循环置换矩阵扩展而成的QC-LDPC码,Fossorier证明了长为2k的环存在的充要条件[11]为
(3)
式中:jk=j0,jb+1≠jb,lb+1≠lb,P为维数。不满足式(3)则校验矩阵中就不存在长为2k的环。
1.1杨辉三角
杨辉三角的构造简单,是大家所熟知的一种数表,如图1所示。
将杨辉三角沿着逆时针方向旋转45°,可以得到

111121133114641..................
图1杨辉三角

(4)
矩阵h具有这样的特点:除第一行与第一列元素以外,其他位置的元素值均为位于本行、上一列的元素与本列、上一行的元素之和。若将这种结构运用到校验矩阵中,只需要存储校验矩阵的第一行和第一列元素,其他元素可以通过简单的加法计算得到,这样能够节省大量的存储空间。若将h矩阵定义为校验矩阵的基矩阵,h中的每个元素都代表着循环移位的次数,由fossorier定理可得扩展后的校验矩阵中存在大量的四环,这会导致译码器不能快速收敛甚至不能收敛。所以,如何将杨辉三角这种简单的构造运用到LDPC码的中,并且使得校验矩阵中不存在四环是需要考虑的一个重要问题。
1.2DY-QC-LDPC码构造
对于一个数列f(n),若n取正偶数,f(n)=(n×n)/2,若n取正奇数,f(n)=(n×n-1)/2,满足这样条件的数列称为大衍数列。结合杨辉三角的构造形式,基于大衍数列构造列重为3或4的规则QC-LDPC码的步骤如下:
1)构造校验矩阵的基矩阵:将基矩阵的第一行置0,第一列除首元素之外依次用大衍数列中的奇数项排列,第二行除首元素之外依次用大衍数列中的偶数项排列,其余位置上的元素采用杨辉三角形式构造。
2)由Fossorier定理检测发现,基矩阵的第二行的前两个元素与第三行的前两个元素构成了四环的存在,这里将第二行的首元素0改为1,这样可以避免四环的出现。
3)基矩阵扩展成校验矩阵,具体方法是:将基矩阵中的0元素用单位矩阵替换,将非零元素用相应的移位循环矩阵替换。
由步骤1)基矩阵的构造方法可以看出:编码器只需要存储第一、二行与第一列的元素,其他位置元素可以通过简单的加法计算得到,这样有利于减少存储空间。基矩阵中的各位置上的元素值如式(5),在基矩阵上进行扩展,可以构造出性能优异的中短码长码字。
(5)
式(5)中,对Pj,l=Pj-1,l+Pj,l-1归纳总结得
(6)
P3,l=l[f(3)+f(2)]+f(5)+(l-lk+1)f(2lk),
2≤lk≤l
(7)
根据构造规则,式(6)易得。式(7)成立的证明如下:
1)当l=1时,左式=P3,l=l[f(3)+f(2)],与实际相符。

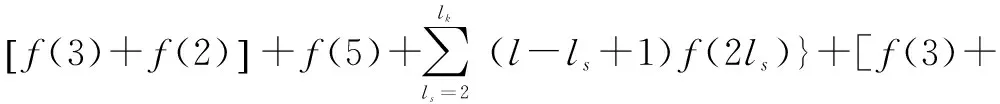
综上,式(7)得证。
2 环分析
新方法构造的基矩阵的行、列上的元素满足这样的两个特点:1)除第一行以外,每行的元素依次呈递增关系;2)每列元素从上到下依次呈递增关系。校验矩阵不含四环,满足式(8),其中j0≠j1,l0≠l1。
Pj0,l0-Pj1,l0+Pj1,l1-Pj0,l1≠0 modP
(8)

1)j0位于第0行、j1位于其他行
Pj0,l0-Pj1,l0+Pj1,l1-Pj0,l1=Pj1,l1-Pj1,l0 (9) 2)j0位于第一行、j1位于第二行 P1,l0-P2,l0+P2,l1-P1,l1=f(2l0)-[f(3)+ (10) 3)j0位于第一行、j1位于第三行 P1,l0-P3,l0+P3,l1-P1,l1=f(2l0)-f(2l1)+{l1[f(3)+ (11) 4)j0位于第二行、j1位于第三行 (12) 综上可知:本文构造的(4,L)QC-LDPC码的校验矩阵中不含四环,(3,L)QC-LDPC码中不含四环的证明与上类似。 本节给出DY-QC-LDPC码在相同参数条件下同其他QC-LDPC码的性能对比,选取1/2码率、BP译码算法、BPSK调制方式、最大迭代次数40次,在AWGN信道下进行仿真实验。首先给出列重为3的DY-QC-LDPC码的性能,以(3,6)DY-QC-LDPC码为例,该码的基矩阵为 (13) 将基矩阵中的0元素用维数为210×210的单位矩阵替换,其他位置用对应的循环置换矩阵替换。图2给出了相同的码长、码率以及仿真环境下,DY-QC-LDPC(1260,630)码与大衍数列码[10]和两类二次函数码(QF-LDPC)[12]的性能对比。由图可以明显地看出大衍数列不适合构造短码长的码字,DY-QC-LDPC码性能优于二次函数码。在误码率为10-6时,DY-QC-LDPC码比QF-LDPC的两种码字性能提高约1 dB左右,具有更好的纠错性能。 图2 列重为3的DY-QC-LDPC(1 260, 630)码和其他码的性能比较 式(10)给出了(4,8)DY-QC-LDPC码的基础矩阵,将基础矩阵中的元素用相应的757×757的循环移位矩阵替换,可以得到码长为6 056的DY-QC-LDPC码。图3给出了DY-QC-LDPC(6 056, 3 028)码和相同参数(码长、码率以及仿真环境)下的其他码字性能对比。在误码率为10-6时,DY-QC-LDPC码相对于文献[13]中所提出的WMC-OCS和QC-OCS码分别有0.1dB、0.2dB的净编码增益,且没有明显的错误平层。同时由大衍数列码的仿真曲线可以看出文献[10]中的构造方法也不适合于中码长码字的构造。 (14) 图3 列重为4的DY-QC-LDPC(6 056, 3 028)码和其他码的性能比较 结合杨辉三角结构,本文基于大衍数列构造出了一种围长至少为6、列重为3或4的规则DY-QC-LDPC码。准循环特性使得它易于硬件实现,并且由于基矩阵的构造借鉴了杨辉三角的结构形式,所以编码器只需要存储0元素以及大衍数列的项,其他元素可以根据其位置通过简单的加法计算得到,这样可节省存储空间。在相同的参数条件下,与大衍数列码、QF-LDPC、WMC-OCS和QC-OCS码相比,仿真结果表明中短长度的DY-QC-LDPC码具有优异的纠错性能。 [1]GALLAGERG.Low-densityparity-checkcodes[J].IEEEtransactionsoninformationtheory, 1962, 8(1):21-28. [2]MACKAYDJC.Gooderror-correctingcodesbasedonverysparsematrices[J].IEEEtransactionsoninformationtheory, 1999, 45(2):399-431. [3]HUXY,ELEFTHERIOUE,ARNOLDD.M.Regularandirregularprogressiveedge-growthtannergraphs[J].IEEEtransactionsoninformationtheory, 2005, 51(1):386-398. [4]HUANGS,TIANFF,JIAXT.AnovelconstructionmethodofLDPCcodesoverfinitefieldintheopticalcommunicationsystem[J].Actaphotonicasinica, 2014,43(6):1-4. [5]HUANGQ,DIAOQJ,LINS.CyclicandQuasi-CyclicLDPCcodesonconstrainedparity-checkmatricesandtheirtrappingsets[J].IEEEtransactionsoninformationtheory, 2012, 58(5):2648-2671. [6]YUANJG,LICY,HUANGS,etal.AnovelconstructionmethodofQC-LDPCcodesforopticalcommunicationsbasedontheBIBDandcirculantdecomposition[J].Journalofoptoelectronics·laser, 2013, 24(9):1698-1701. [7]LAN L, TAI Y Y, LIN S. New constructions of quasi-cyclic LDPC codes based on special classes of BIBD's for the AWGN and binary erasure channels[J]. IEEE transactions on communications, 2008, 56(1):39-48. [8]ESMAEILI M. 4-Cycle free LDPC codes based on difference sets[J]. IEEE transactions on communications, 2012, 60(12):3579-3586. [9]ZHANG L J, LI B. Constructions of QC LDPC codes based on integer sequences[J]. Science China, 2014, 57(6):1-14. [10]ZHU L J, WANG H, SHI Y S. Method for constructing QC-LDPC codes using the dayan sequence[J]. Journal of Xidian University, 2012, 39(3):144-160. [11]FOSSORIER M P C. Quasi-cyclic low-density parity-check codes from circulant permutation matrices[J]. IEEE transactions on information theory, 2004, 50(8):1788- 1793. [12]ZHANG G H, SUN R. Deterministic construction of girth-eight (3, L) QC-LDPC codes from quadratic function[J]. Electronics letters, 2013,49(9):600-602. [13]HUANG J F, HUANG C M, YANG C C. Construction of one-coincidence sequence quasi-cyclic LDPC codes of large girth[J]. IEEE transactions on information theory, 2012, 58(3):1825-1836. 黄胜(1974— ),教授,主要研究方向为信道编码和下一代网络; 穆攀(1990— ),女,硕士生,主研信道编码; 张睿(1991— ),女,硕士生,主研信道编码; 袁建国(1968— ),教授,主要研究方向为光通信技术与光电子技术。 责任编辑:薛京 Method of construction of regular QC-LDPC codes based on Dayan sequence HUANG Sheng, MU Pan, ZHANG Rui, YUAN Jianguo (KeyLaboratoryofOpticalCommunicationandNetwork,ChongqingUniversityofPostsandTelecommunications,Chongqing400065,China) According to structure of Yanghui Triangle and based on the Dayan sequence, a novel construction method of regular quasi-cyclic low-density parity-check (QC-LDPC) codes whose column weight is 3 or 4 is put forward. Girth of parity-check matrix is at least 6. Length of the code can vary flexibly. And storage spaces can be saved. Under the same parameters, at the bit error rate(BER) of 10-6, simulation results show QC-LDPC(1260, 620)code with column weight 3 has a net coding gain(NCG) nearly 1 dB more than quadratic function code and the NCG of QC-LDPC(6056, 3028) code with column weight 4 is 0.1 dB and 0.2 dB more than WMC-OCS and QC-OCS code respectively. regular QC-LDPC code; Yanghui triangle; Dayan sequence TN911 A 10.16280/j.videoe.2016.09.015 国家自然科学基金项目(61171158);重庆市自然科学基金项目(cstc2013jcyjA40052;cstc2012jjA40060);重庆市教委科学技术研究项目(KJ130515) 2016-01-08 文献引用格式:黄胜,穆攀,张睿,等. 基于大衍数列的规则QC-LDPC码构造方法[J]. 电视技术,2016,40(9):77-80. HUANG S, MU P, ZHANG R,et al. Method of construction of regular QC-LDPC codes based on Dayan sequence [J]. Video engineering,2016,40(9):77-80.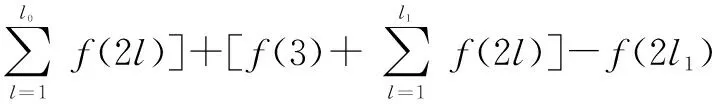


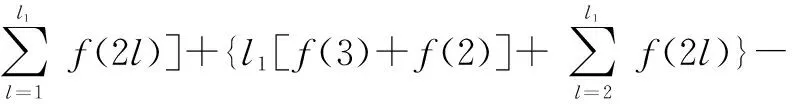
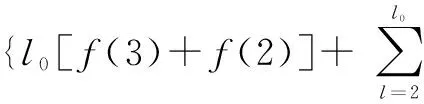
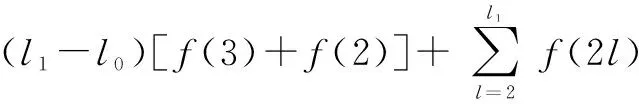
3 仿真分析




4 总结

