3×4矩阵变换器新型调制策略的研究

付光杰，刘淄航，刘文福，张雷

（1.东北石油大学，黑龙江大庆163318；2.大庆石化公司炼油厂，黑龙江大庆163711；3.天津修船技术研究所，江苏徐州300456）

3×4矩阵变换器新型调制策略的研究

付光杰1，刘淄航1，刘文福2，张雷3

（1.东北石油大学，黑龙江大庆163318；2.大庆石化公司炼油厂，黑龙江大庆163711；3.天津修船技术研究所，江苏徐州300456）

3×4矩阵变换器具有优良的带不平衡负载能力，针对该矩阵控制算法非常复杂，控制难度大的缺点，采用直接检测输入输出侧的电压与电流信号的方法，简化了常规的第N相占空比计算、虚拟逆变、虚拟整流的SVPWM调制策略，达到谐波及脉动成分小，线电压扇区判断及占空比计算准确的目的。通过仿真验证了该系统可输出较为理想的三相对中性线的对称波形，具有速度快、稳定性好、精度高等优点。

3×4矩阵变换器；三相不平衡负载；直接检测；线电压扇区判断；占空比计算

矩阵变换器MC（Matrix Converter）有无中间直流环节、能量直接传递且双向流动等优点，很有发展前景。在实际应用中，3×3矩阵带不对称负载具有很大的局限性。对于现有的3×4矩阵该矩阵调制策略过于繁琐，使控制难度加大且输出含有大量谐波。基于上述原因本文采用直接检测电压电流，优化虚拟整流、虚拟逆变环节，最后联合两个环节得到3×4矩阵的调制策略。并且应用搭建仿真验证理论的正确性。

1　3×4矩阵拓扑结构及数学模型

图1（a）为3×4矩阵拓扑结构图，图1（b）等效电路拓扑结构，负载为阻感负载，N相与中性点连接[1]。

矩阵变换器分析过程，等效成交⁃直⁃交拓扑结构进行，并分为虚拟整流、虚拟逆变、消去中间虚拟的直流环节三部分。图1（b）即为等效后的交⁃直⁃交路拓扑结构。a,b,c为输入侧；p,n为虚拟的直流环节；u,v,w,N为输出侧。图中输入侧不能短路，输出侧不能开路，即每一相只有一个开关导通。

图1　主电路拓扑结构与等效电路拓扑结构

图1中虚拟整流部分开关函数为Sik、虚拟逆变部分开关函数为Skj，则有式（1）的输入/输出关系[2]：

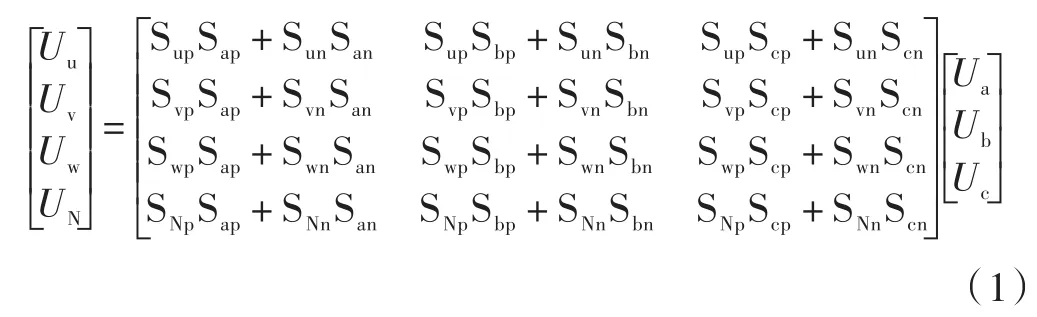
所以只需调节式（1）中的开关矩阵，就起到了调节矩阵变换器的目的。

2　新型虚拟逆变SVPWM调制策略

图2为逆变侧电压空间矢量调制图[4]。图2（a）为电压空间矢量图，其中6个非零矢量分别位于正六边形的6个顶点位置，并且将空间划分为Ⅰ⁃Ⅵ六个扇区。2个矢量，位于原点位置。图2（b）为在第一扇区内的合成，这也是计算占空比的依据。简化虚拟逆变，主要是使扇区判断与占空比计算两个环节更加简洁。

图2　虚拟逆变侧空间矢量调制

2.1扇区判断

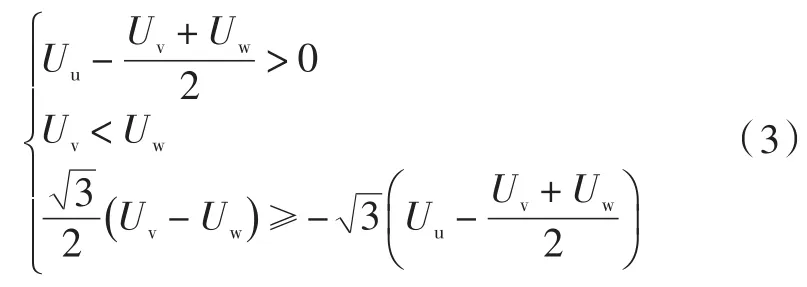
整理式（3）可知，在第一扇区内的最大电压为Uu，最小电压为Uv。则扇区的判断依据可表示为：max(|Uuv|,|Uvw|,|Uwu|)=Uuv，同理其他扇区的判断以此类推。

2.2占空比的计算

在图2（b）中根据正弦定理得出常规调制策略中所应用的占空比算式[4]如下：

2017年夏，我们在庐山认识了李汝庆先生。他的祖父李祥卿，曾参与庐山别墅群的修建，他家的“李广记营造厂”比宋子文岳父的“张兴记”还要早得多。20世纪60年代，李汝庆先生还与赫赫有名的王震将军结下不解之缘。已经88岁高龄的李汝庆先生，头脑清醒，思路清晰，记忆力也很好。他告诉我们，他已连续8年从广州来到庐山度夏。在庐山，他领我们去寻访祖父当年留下的遗迹，看合面街他家的旧址，指点“李广记营造厂”当年建造的别墅。在他租住的屋内，李老连续数日讲述了李氏家族起伏跌宕的历史和他奇特的人生际遇。

如果采用式（4）的占空比调制，需要电压矢量的幅值、复平面内的夹角以及虚拟直流侧的电压三个变量，正是由于复杂的计算导致了算法的冗余。因此为了能够使占空比的计算更加简便，分别分析式（4）中的，θ。图2（a）中的矢量电压与三相电压有如下关系式：

根据三角函数关系角θ有如下关系式：

式（5），式（6）代入到式（4）中得出本文所应用的占空比：

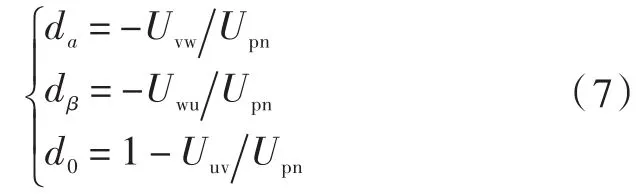
式（7）较式（4）占空比的计算量大幅减小，式（7）中的占空比只是简单的比值，且不需要计算复平面内的角度，因此无论是在计算的精度上，还是速度上都得到了相应的提高。

由于输入电压与电流同相位，则常规的第N相占空比[3]计算如下：

将本文简化后的式（7）中占空比dα，dβ相加，代入式（8），即为本文所推导出的占空比计算式：

式中的占空比计算只需要检测输出侧的最大线电压即可，较式（4）中常规的第N相占空比的计算量有所减少。

3　新型虚拟整流调制策略

3.1扇区判断

与虚拟逆变级同理，虚拟整流级的区间判断依然以第i区间为例，此处有max(ia,ib,ic)=ia其他扇区的判断依据以此类推。

3.2计算占空比

对于占空比的计算，本文以第i区间为例，其他区间同理，计算相应的占空比[3]即：

为了化简虚拟整流侧的占空比，由式（10）可得：ia=(dμ+dγ)⋅Ipn，ib=-dμIpn，ic=-dγ。整理与化简进一步得到本文的占空比计算式：

式（11）的占空比计算式达到了与虚拟逆变侧同等的简化效果。

4　消去直流环节

首先排列第N相的开关顺序，为了尽量减少开关动作次数，避免开关损耗，输入电压在Ⅰ，Ⅲ，Ⅴ区间按组合1（a，b，c，a，a）次序，而Ⅱ，Ⅳ，Ⅵ则按照组合2（b，a，c，b，b）次序进行切换[3]。

联合新型虚拟整流与虚拟逆变的调制策略，消去中间直流环节[5]。为了不失一般性，仍以第一扇区为例，其中逆变侧含有，整流侧含有，分别两两组合，形成含有零矢量的共5种状态。如表1所示。

表1　矢量组合与开关实例

5　仿真验证

本文基于Matlab/Simulink及S函数搭建仿真模型。系统参数：380 V，50 Hz三相可编程交流电源，设定输出频率为30 Hz，负载采用阻感负载，其中R=15 Ω L=30 mH。不平衡负载电阻分别为15 Ω，10 Ω，7 Ω，L=30 mH。

通过对该系统带平衡负载时的仿真，可得图3所示的输出仿真结果。由图可知输出侧电压与电流均三相对称。由于整个系统输出线电压，直接由程序线电压信号指令控制，所以谐波及脉动成分为零。平衡负载时中性点电位为零，N相桥臂中并无电流流过，所以图中iN幅值为零。系统在0.01 s左右达到稳定状态。在0.05 s处加入扰动后，间隔0.02 s再次进入稳定状态，充分验证了该系统具有很强的抗扰动性。

图3　对称负载时三相输出电压与电流

通过带对不平衡负载时的仿真，输出侧的电流波形仿真结果如图4所示。其中电压波形同图3中无扰动时的电压波形。分析图4可知，由于系统带不平衡负载，所以输出侧的电流波形已不再是三相对称的。由于中性点发生了移动，所以导致N相中电流不再为零。而对于输出侧的电压，只是相对于第N相对称。

图4　不平衡负载时输出侧电流

图5是输入级中a相的电压与电流波形仿真结果，电流波形近似于正弦波。由于系统输入侧滤波器中电容的影响，电流波形略超前电压，但是功率因数仍然接近于1，对整体影响不大。图6为a相电流在未加入滤波器时的频谱分析结果，谐波畸变率小，满足电流的要求，验证了3×4矩阵具有优良的带不平衡负载的能力。

图5　a相输入电压与电流波形

图6（a）为a相电流在未加入滤波器时的频谱分析结果，谐波畸变率为1.83%满足电流的要求；图6（b）为3×3矩阵带不平衡负载时a相的频谱图，谐波畸变率为13.52%，远远高于前者。从而验证了3×4矩阵具有优良的带不平衡负载的能力。

图6　频谱分析

6　结语

本文通过简化矩阵变换器的调制策略，缩短了系统达到稳定的时间，提高了带不对称负载的能力与系统的精度。尽管负载的不平衡，系统仍然可以输出较为理想三相对中性线的对称波形。该系统不但输出侧不含次谐波，同时满足了负载对电压的需求。输入侧的电流波形达到正弦的标准，且功率因数接近于1，凸显了他的能量直接传动传输效率高等特点。

[1]KOBRAVI K，IRAVANI R，KOJORI H A.Three⁃leg/four⁃leg matrix converter generalized modulation strategy⁃part I：a new formulation[J].IEEE Transactions on Industrial Electronics，2013，60（3）：848⁃859.

[2]粟梅李，丹云，孙尧，等.双级矩阵变换器的过调制策略[J].中国电机工程学报，2008（3）：47⁃52.

[3]王汝田.矩阵变换器的调制策略研究[D].哈尔滨：哈尔滨工业大学，2009.

[4]郭有贵，喻寿益，朱建林.提高矩阵变换器电压传输比的新型调制策略[J].控制理论与应用，2006，23（4）：542⁃546.

[5]汤宁平，王建宽，吴汉光.矩阵变换器的SPWM控制技术及其实现[J].电工技术学报，2003（4）：25⁃29.

[6]胡文丽，赵永涛，郑永强.一种新型矩阵式高频链逆变器控制方法[J].现代电子技术，2012，35（19）：188⁃190.

Research on new modulation strategy of 3×4 matrix converter

FU Guangjie1，LIU Zihang1，LIU Wenfu2，ZHANG Lei3
（1.Northeast Petroleum University，Daqing 163318，China；2.Refinery of Daqing Petrochemical Company，Daqing 163711，China；3.Tianjin Shiprepairing Technology Research Institute，Xuzhou 300456，China）

The 3×4 matrix converter has excellent unbalanced load capacity，for its control algorithm is complex and diffi⁃cult to control，the method of direct detection for the voltage and current signals on the input and output sides is adopted，which can simplify the conventional SVPWM modulation strategies of N⁃phase duty⁃cycle calculation，virtual inversion and virtual rec⁃tification，and achieve the little harmonic and pulsation component，and accurate line voltage sector judgment and duty cycle calculation.The simulation results verify that the system can output perfect three⁃phase symmetrical waveform，and has fast speed，good stability and high precision.

3×4 matrix converter；three⁃phase unbalanced load；direct detection；line voltage sector judgment；cancula⁃tion of duty⁃cycle

TN911⁃34

A

1004⁃373X（2016）02⁃0155⁃04

10.16652/j.issn.1004⁃373x.2016.02.043

付光杰（1962—），女，黑龙江大庆人，教授，博士生导师，博士，现任东北石油大学电气信息工程学院副院长、东北石油大学省级重点专业“电气工程及其自动化”学科带头人。从事电气工程与自动化领域的教学和科研工作。主要研究方向为电力系统安全运行及其自动化、电力电子技术及应用和电力传动自动化系统。

刘淄航（1987—），男，黑龙江庆安人，在读硕士研究生。研究方向为电力电子与电力传动。

2015⁃07⁃26