基于分位回归的风险保费预测

杨　亮，孟生旺

(中国人民大学 a.应用统计科学研究中心; b.统计学院, 北京100872)



【统计应用研究】

基于分位回归的风险保费预测

杨亮a,b，孟生旺a,b

(中国人民大学 a.应用统计科学研究中心; b.统计学院, 北京100872)

风险保费预测是非寿险费率厘定的重要组成部分。在传统的分位回归厘定风险保费中，通常假设分位数水平是事先给定的，缺乏一定的客观性。为此，提出了一种应用分位回归厘定风险保费的新方法。基于破产概率确定保单组合的总风险保费，建立个体保单的分位回归模型，并与总风险保费建立等式关系，通过数值方法求解出分位数水平，实现对个体保单风险保费的预测。通过一组实际数据分析表明，该方法具有良好的预测效果。

保费原理；风险保费；分位回归；Tweedie回归

一、引 言

非寿险保费由纯保费、风险附加、费用附加和利润附加构成。纯保费用于补偿保险公司的期望赔款支出。风险附加用于支付实际损失中超过纯保费的不利偏差所导致的额外赔款支出。费用附加用于支付保险公司的经营管理费用。利润附加是对保险业务占用资本金的一种合理补偿。在保险实践中，广泛使用的费率厘定方法为：首先，应用广义线性模型等方法预测纯保费；其次，应用保费原理计算风险附加；最后，根据经验数据确定费用附加和利润附加。纯保费与风险附加之和称为风险保费。

纯保费的厘定方法主要包括广义线性模型及其推广模型。广义线性模型作为非寿险费率厘定的标准方法，首次由McCullagh等人将其应用于精算领域[1]296-300，后来逐步得到广泛应用[2][3]121[4]。基于广义线性模型的费率厘定方法，通常假设因变量服从指数分布族，如索赔次数服从泊松分布或负二项分布，索赔强度服从伽马分布或逆高斯分布，纯保费服从Tweedie分布，并在此基础上建立广义线性模型对索赔频率、索赔强度或纯保费的均值进行预测。为了解决费率厘定中的一些特殊问题，如连续型协变量的非线性影响和因变量的组内相关性等，还可以将广义线性模型进一步扩展。譬如，在广义线性模型中引入连续型协变量的平滑函数，就可以将广义线性模型推广到广义可加模型，该模型解决了连续型协变量与因变量之间的非线性关系问题[5][6]136-174。如果将协变量的系数由固定未知参数扩展到服从特定分布的随机参数，就可以将广义线性模型推广到广义线性混合模型，该模型可以有效地度量因变量的组内相依结构[7][8]9-21[9]。对位置参数、尺度参数、形状参数同时建立回归的广义可加模型，是对广义线性模型、广义可加模型和广义线性混合模型的进一步推广，该模型可以从多个角度对研究对象进行刻画[10]337-345[11]。

在纯保费的基础上，应用保费原理可以求得风险附加，然后将二者相加就得到了风险保费。常用的保费原理包括期望值原理和标准差原理。譬如，应用期望值原理计算的风险保费等于纯保费加上纯保费的一个百分比，而应用标准差原理计算的风险保费等于纯保费加上标准差的若干倍。应用保费原理计算风险附加往往存在一定的理论缺陷，譬如，在期望值原理中，风险附加是纯保费的一定比例，这就意味着纯保费越大，损失的不确定性也越大，而现实情况显然并非如此。在标准差原理中，虽然应用标准差在一定程度上反映了损失的不确定性，但对于长尾损失而言，标准差对不确定性的度量也不够准确。

在预测纯保费时，无论是应用广义线性模型、广义可加模型、广义线性混合模型，还是应用对位置参数、尺度参数、形状参数同时建立回归的广义可加模型，它们都要对因变量的分布类型做出假设，且预测结果容易受到数据中异常值的影响。在应用保费原理计算风险附加时，由于仅仅考虑了损失分布的期望值或标准差，未能准确反映损失的波动性和尾部特征，所以也会导致一定的偏差。

与均值回归模型相比，分位回归具有下述优点：第一，分位回归无需分布假设，增加了模型的灵活性；第二，参数估计受异常值的影响较小，估计结果更加稳健；第三，分位回归描述了自变量对因变量不同分位点的影响，可以更为有效地解释分布的尾部特征。有鉴于此，基于分位回归计算风险保费的应用受到很多关注[12-13]。但是，目前的研究成果仅仅讨论了在个体保单层面应用分位回归的问题，譬如在99%的可靠性水平下，把保单损失的99%分位数作为风险保费，然后把每份保单的风险保费相加即得整个保单组合的风险保费。这种做法的缺陷是，对于个体保单而言，风险保费可以保证实际损失超过风险保费的概率不会超过1%，但对于整个保单组合而言，由于个体保单之间存在一定的风险分散作用，保单组合的累积损失超过总风险保费的概率就不会是1%，很可能远远小于1%，也就是说，这种方法求得的风险保费是偏高的。合理的风险保费应该确保整个保单组合的实际损失超过风险保费的概率被控制在一个可以接受的水平，如不超过1%。

本文的主要贡献有：第一，基于分位回归提出了一种自上而下计算风险保费的新方法，即在给定的可靠性水平下，首先计算保单组合的总风险保费，然后应用数值算法和分位回归将其分解到每份保单上，使得每份保单的风险保费之和等于保单组合的总风险保费。这种方法可以保证整个保单组合的实际损失之和超过总风险保费的概率被控制在一个可以接受的概率水平之内。第二，在应用标准差原理厘定风险保费时，基于已经求得总风险保费计算每个保单的风险附加，改进了传统方法对风险保费的计算结果。第三，基于中国汽车保险的实际损失数据，对风险保费的各种厘定方法进行了比较研究。

二、分位回归

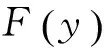
(1)

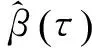
(2)

当τ=0.5时，就是中位数回归，其回归系数使得残差的绝对值之和达到最小：

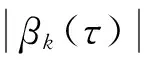
分位回归具有优良的统计性质，能全面考察因变量的分布特征，在经济、金融和保险等领域的应用受到越来越多的关注[12-14]。

三、风险保费

(3)

在应用标准差原理计算风险保费时，首先，通过回归模型预测每个风险类别的期望损失(即纯保费)及其标准差；其次，利用期望损失加上α倍的标准差得到风险保费。

在保费的构成中，之所以要包括一定的风险附加，其目的是为了应对随机损失所带来的不利偏差，从而确保保险公司收取的风险保费不足以支付实际损失的概率很小，如小于1%。这就意味着，保险公司收取的风险保费总额应该大于实际损失总额的99%分位数。上述的标准差原理显然无法满足这个总体性要求。此外，对于每份保单而言，其风险附加的大小也应该与其损失分布有关，譬如，越是右偏的损失，风险附加应该越大。标准差原理虽然可以在一定程度上反映损失分布的离散程度和右偏性，但其效果远不及分位数，因为后者可以对损失分布的右偏性进行完整刻画。由此可见，应用标准差原理计算风险附加，不能保证风险附加在总体上的充足性以及在不同保单之间分配的合理性。

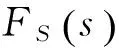
假设保单组合的总风险保费为C，则保险公司的累积赔款超过总风险保费C的概率(即保险公司破产的概率)可以表示为：

(4)

由此可以求得总风险保费应为：

(6)

(一)基于标准差原理计算个体保单的风险保费

在实际保险业务中，大多数保单不会发生索赔，只有少数保单会发生索赔，所以个体保单在一个保险期间的累积损失Y在零点会有一个较大的概率堆积，表示没有发生索赔的概率。在对个体保单的累积损失观察值建模时，通常假设Y服从零调整逆高斯分布或Tweedie分布[15]216-217。

当Y服从零调整逆高斯分布时，其密度函数可以表示为

(7)

其中μ>0,σ>0,0<ν<1。零调整逆高斯分布的均值和方差分别为：

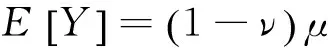
(8)

(9)

应用式(8)和式(9)，可以求得应用标准差原理计算的风险保费为：

(10)

在零调整逆高斯分布的参数μ中引入解释变量xi，可建立如下回归模型：

如果进一步要求所有保单的风险保费之和等于总风险保费C，则应有如下等式成立：

从上式可以求出风险附加的比例α，再应用式(10)，就可以求得每份保单的风险保费。

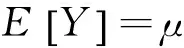
(11)

(12)

在标准差原理下，风险保费可以表示为：

(13)

对Tweedie分布的均值参数μ中引入解释变量xi，可建立如下回归模型：

如果进一步要求所有保单的风险保费之和等于总风险保费C，则应有如下等式成立：

(14)

从上式可以求解出风险附加的比例α，再应用式(13)，就可以求得每份个体保单的风险保费。

(二)基于分位回归计算个体保单的风险保费

由于许多保单在保险期间不会发生索赔，所以它们的损失观察值为零。此时，普通的分位回归将不再适用，需要采用零调整分位回归模型[13]。建立零调整分位回归模型的具体过程如下。

(15)

其中p为保单发生索赔的概率。由公式(15)可知，当y=0时，有：

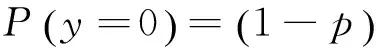
当y>0时，有：

因此，含零损失Y的τ分位数可以表示为：

(16)

上式表明，含零损失Y的τ分位数可以通过非零损失Y*的τ*分位数求得，且满足：

(17)

由式(17)容易看出，τ*<τ，且τ*关于p单调递增。

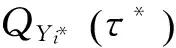
(18)

求解式(18)可以利用分位回归的单调同变性，即

四、实证分析

以下基于国内某保险公司的车损险数据进行实证分析。数据来源可参见孟生旺的《回归模型》[15]220。

(一)数据描述

在本例的数据中，因变量是每个风险类别中平均每个车每年的索赔金额，解释变量如表 1所示，包括车主年龄、车龄、续保类型、驾驶人性别和保单持有人所在地区，其中车主年龄和车龄是连续变量，续保类型和保单持有人所在地区是分类变量。本文选取车年数为1的73 500份保单进行分析，其中发生了52 853次索赔，涉及33 029份保单，总的索赔金额为104 772 648元。

表1　变量描述

索赔金额的直方图呈现出明显的尖峰厚尾特征(图1)，偏度和峰度分别为88.161和16 315.430，远远大于正态分布的偏度和峰度(分别为0和3)。

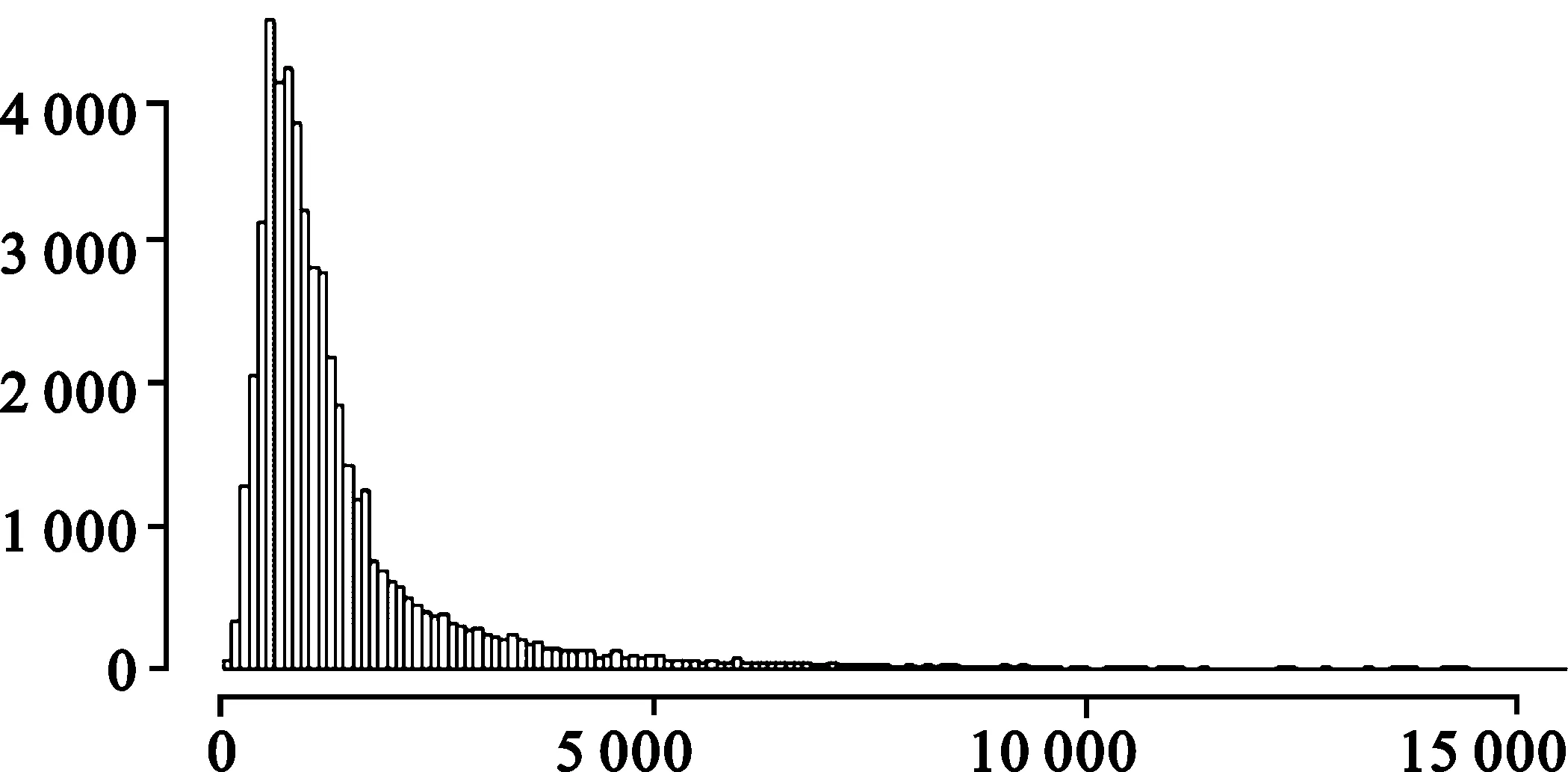
图1　索赔金额的直方图

(二)保单组合的总风险保费

为了计算保单组合的总风险保费，首先需要求得该保单组合总索赔额的分布。图 1是单次索赔额的直方图。从该图可以看出，单次索赔额呈现出明显的尖峰厚尾特征，但根据中心极限定理，当索赔次数足够大时，保单组合的总索赔额将近似服从正态分布。

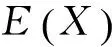
E(S)=E(N)E(Xi)=104 772 648

=1 404 6442

根据正态分布的性质，累积损失99%分位数为108 040 339。换言之，如果将该保单组合的总风险保费确定为C = 108 040 339，则保险公司收取的风险保费不足以支付索赔的概率不会超过1%。

(三)个体保单的风险保费

在求得保单组合的总风险保费以后，需要将其分摊到每份保单上。由于每份保单的累积赔款在零点存在概率堆积，所以在均值回归中需要采用零调整逆高斯回归或Tweedie回归，并在分位回归中采用零调整分位回归。在零调整分位回归中，用数值方法求得的分位数水平为τ*=50.15%。模型的参数估计结果如表 2所示。从表 2可以看出，分位回归与均值回归选取的解释变量基本一致，大多数回归系数的符号也完全相同。

表2　模型的参数估计值

从理论上讲，风险保费应该是赔款的某个分位数，所以应用分位回归求得的风险保费在理论上更加合理。图 2揭示了应用均值回归模型和标准差原理计算的风险保费可能带来的偏差。从总体上看，应用均值回归计算的风险保费在某些风险类别上偏低，而在另外一些风险类别上偏高。这是因为基于零调整逆高斯回归和Tweedie回归计算的风险保费，都是按照标准差的一个百分比作为风险附加，容易受到观察数据中异常值的影响。应用分位回归求得的风险保费与各个风险类别的50.15%分位数比较接近，不易受观察数据中异常值的影响，所以没有过于偏高或偏低的费率厘定值。

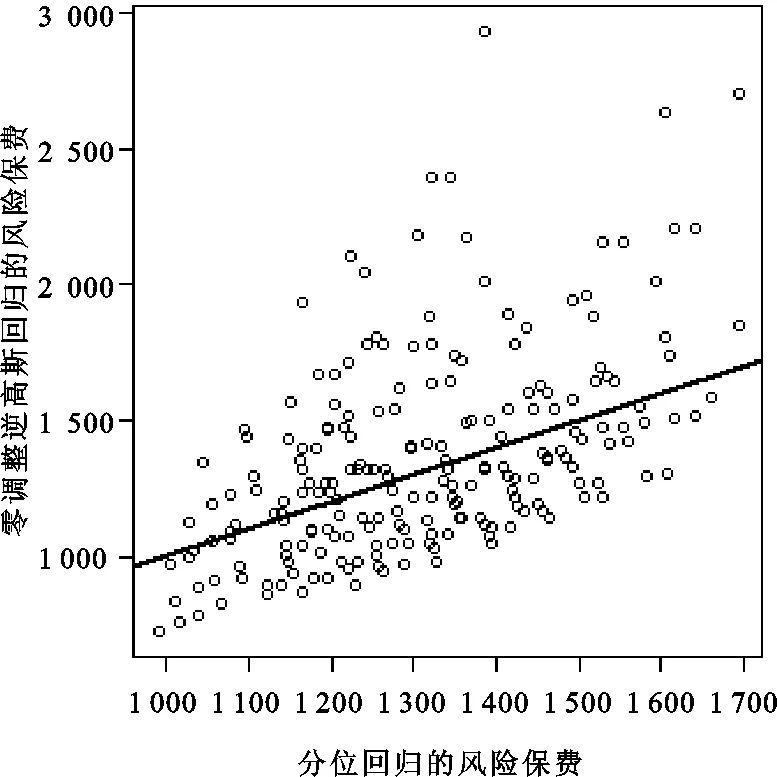
图2　均值回归与分位回归的风险保费

五、小 结

在传统的费率厘定中，通常应用均值回归模型求得纯保费，然后在纯保费的基础上按照标准差的一定百分比计算风险附加。纯保费与风险附加之和就是所谓的风险保费。风险保费从本质上讲应该是损失的一个分位数，从而使得实际损失超过风险保费的概率被控制在一个可以接受的水平，如1%。因此，应用分位回归模型直接对风险保费进行预测具有理论上的优势。

在应用分位回归厘定风险保费的现有文献中，都没有解决如何确定分位数水平的问题。本文在给定保单组合破产概率的条件下，求得保单组合的总风险保费，然后用数值方法求得分位数水平，最后基于分位回归厘定了每份保单的风险保费。应用这种方法求得的风险保费具有两个特点：一方面可以保证公司的破产概率被控制在一个可以接受的水平，如不超过1%，另一方面可以保证每份保单的风险保费之和等于保单组合的总风险保费。

基于一组数据的实证研究结果表明，应用分位回归计算的风险保费不易受数据中异常值的影响，而均值回归容易受到数据中异常值的影响，从而有可能使得一些保单的风险保费偏大，而另一些保单的风险保费偏小。

[1]McCullagh P N J A. Generalized Linear Models[M]. London: Chapman & Hall, 1989.

[2]孟生旺. 广义线性模型在汽车保险定价的应用[J]. 数理统计与管理, 2007, 26(1).

[3]Piet de Jong，Gillian Z Heller. Generalized Linear Models for Insurance Data [M].Cambridge: Cambridge University Press，2008.

[4]刘兆君.伴随置信度的线性回归模型[J]. 统计与信息论坛, 2015(7).

[5]Hastie T, Tibshirani R.Generalized Additive Models (with Discussion) [J]. Statistical Science, 1986(42).

[6]Hastie T J T R. Generalized Additive Models [M]. London: Chapman & Hall, 1990.

[7]Breslow N E, Clayton D G. Approximate Inference in Generalized Linear Mixed Models [J]. Journal of the American Statistical Association, 1993, 88(421).

[8]Stroup W W.Generalized Linear Mixed Models: Modern Concepts, Methods and Applications[M]. Florida: CRC Press,2012.

[9]孟生旺, 李政宵. 基于随机效应零调整回归模型的保险损失预测[J]. 统计与信息论坛, 2015(12).

[10]Rigby R A, Stasinopoulos D M. The GAMLSS Project: A Flexible Approach to Statistical Modelling[C]//New Trends In Statistical Modelling: Proceedings of the 16th International Workshop on Statistical Modelling, 2001.

[11]Rigby R A, Stasinopoulos D M. Generalized Additive Models for Location, Scale and Shape (with Discussion) [J]. Journal of the Royal Statistical Society: Series C (Applied Statistics), 2005, 54(3).

[12]Pitselis G.Quantile Regression in a Credibility Framework[C]∥11th International Congress Insurance:Mathematics and Economics,2007.

[13]Kudryavtsev A A. Using Quantile Regression for Rate-making[J]. Insurance: Mathematics and Economics, 2009(2).

[14]Koenker R, Bassett G. Regression Quantiles [J]. Econometrica, 1978, 46(1).

[15]孟生旺. 回归模型[M]. 北京：中国人民大学出版社, 2015.

(责任编辑：李勤)

Prediction of Risk Premium Based on Quantile Regression

YANG Lianga,b, MENG Sheng-wanga,b

(a. Center for Applied Statistics;b. School of Statistics, Renmin University of China, Beijing 100872, China)

Prediction of risk premiums is an important part in the non-life insurance premium ratemaking. During the determining the risk premium in the traditional quantile regression, quantile level is generally given in advance, which is lack of objectivity. Therefore, we propose a new method for determining the risk premium by applying of quantile regression. Firstly, determining the total risk premiums based on the probability of bankruptcy; secondly, to establish quantile regression model in individual policies, and establish relationships with total risk premium; finally, to solve for quantile level by numerical methods, obtain the individual risk premiums. Basing on a set of actual data, the results demonstrates that the method has high forecasting accuracy.

premium principle; risk premium; quantile regression; Tweedie regression

2016-05-18

国家自然科学基金项目《考虑风险相依的非寿险精算模型研究》(71171193); 教育部重点研究基地重大项目《随机效应模型及其在非寿险风险管理中的应用》(12JJD790025)

杨亮，男，安徽阜阳人，博士生，研究方向：非寿险精算与统计模型；

F840∶O212

A

1007-3116(2016)09-0083-06

孟生旺, 男, 甘肃秦安人，经济学博士，教授, 博士生导师，研究方向：应用统计，风险管理与精算。