基于偏好变量的指数跟踪方法
王 娜,钱争鸣
(厦门大学 经济学院,福建 厦门 361005)
【统计理论与方法】
基于偏好变量的指数跟踪方法
王娜,钱争鸣
(厦门大学 经济学院,福建 厦门 361005)
考虑到在进行指数跟踪时影响强度大并且流动性好的成份股往往是被偏好的,结合股票市场的网络结构和指数的编制规则,提出基于偏好变量的指数跟踪方法;对沪深300指数进行实证分析,从跟踪偏离度、平均超额收益和年跟踪误差三方面对新方法进行评估,并与非负LASSO模型进行对比分析。实证结果显示,新方法不仅优于非负LASSO模型,而且优于市场上大多数指数基金。
无标度网络;影响强度;流动性;指数跟踪
一、引 言
指数化投资发展迅速,好的指数跟踪技术能使投资者较精准地复制标的指数的市场表现,从而获得更高的收益。
指数跟踪方法分为完全复制法和非完全复制法。完全复制法,就是完全复制标的指数中的所有成份股,并把标的指数编制中的权重作为跟踪股票组合中每只股票的相应权重;非完全复制法,即用一定的策略选取部分成份股构成股票组合并计算股票组合中每只成份股的权重,以达到复制标的指数的目的。
跟踪股票组合的目标是取得与标的指数基本一致的收益,所以跟踪股票组合收益和标的指数收益之间的偏离程度就成为评价跟踪股票组合优劣的一个重要指标。偏离程度可以用跟踪偏离度、平均超额收益率和跟踪误差来衡量。
完全复制法虽然在理论上应获得样本内较小甚至为零的偏离程度,但是当标的指数包含的成份股较多或者含有流动性不足的成份股时,非完全复制法会更好。非完全复制指数跟踪方法其实也很多,但传统的分层抽样法受主观因素影响较大,神经网络等机器学习算法又非常复杂,所以指数跟踪问题一直困扰着学术界和实务界。之后,有学者提出用高维变量选择方法挑选股票,并取得了良好的效果。
高维变量选择方法是近几年兴起的一类变量选择方法,不仅在生物医学中有广泛的应用,而且也逐渐被引入到指数跟踪研究领域。子集选择法是比较经典的高维变量选择方法,但此法不仅不稳定,而且受数据的影响很大。岭回归方法虽然较子集选择法更稳定,但岭回归只压缩系数,不剔除变量,达不到挑选变量的效果。所以Tibshirani提出了LASSO(Least Absolute Shrinkage and Selection Operator)方法[1]。LASSO方法不仅克服了子集选择法和岭回归方法的缺点,而且可以同时进行变量选择和参数估计,成为高维变量选择的流行方法,在指数跟踪领域也是优先被使用的高维变量选择方法;梁斌和Lan Wu等考虑到中国A股市场虽然有融券做空机制,但是发展一直都很缓慢,对LASSO模型进行了改进,提出非负LASSO模型,并用此算法完成了成份股的选取,实证结果表明非负LASSO模型表现较好[2-3];马景义等人将市场景气因素应用到非负LASSO模型中,得到了含景气参数的非负LASSO指数跟踪算法[4];不过,LASSO估计出来的参数是有偏的,所以后来有很多学者对LASSO进行了不同的改进,Zou提出的Adaptive LASSO(自适应LASSO)对惩罚项系数进行了自适应加权,并证明在一定条件下,Adaptive LASSO可以满足Oracle性质(即模型选择一致性和参数估计渐进正态性)[5];刘睿智等人使用Adaptive LASSO变量选择方法构造投资组合,证实其对指数的复制效果良好[6]。
但是,目前依旧面临着两个问题,即成份股的选择仍然不稳定,并且一些影响较大或者流动性较好的偏好成份股不能被选上。所以,需要使用专业领域的知识去改进回归模型,得到适用于指数跟踪问题的高维变量选择模型。
影响强度的量化可以从股票价格的网络关系入手。单只股票价格的变化会受到其他股票价格变化的影响,Kim等人对S&P500指数中500只成份股的收益率数据进行修正后计算其交叉相关系数,以500个公司作为500个节点,以交叉相关系数作为边,构建了一个有权复杂网络,定义单个节点上所有边之和为此节点的影响强度[7]。可见,某节点影响强度的绝对值越大,对网络中其他节点股票价格变化的影响越大,在指数跟踪中应该优先选入影响强度绝对值大的股票。同时,节点影响强度绝对值的分布具有幂律特征,即此网络具有无标度的特点(此网络又被称为无标度网络),说明此网络中具有较大影响强度的节点并不是很多[8]。也就是说,优先选入少数几个影响强度绝对值大的股票很可能得到比较理想的跟踪效果,其实已经有不少文献对股票市场具有无标度拓扑特征这个事实进行了验证。Benjamin等人实证了巴西金融证券市场具有无标度网络结构[9];黄玮强等人利用网络知识分析了中国的股市,建立了中国股市中1 080只股票的无标度网络[10]。
把变量的网络特征融入LASSO等高维变量选择模型中进行高维分析,是基因工程领域的一种前沿方法[11-12],但在指数跟踪问题上尚未有人从网络层面考虑过这个问题。基于成份股影响强度的绝对值越大对网络中其他节点股票价格变化的影响越大的事实,有理由认为在使用非负LASSO进行股票挑选时使影响强度绝对值大的股票优先被选入是合理的。
流动性的量化可以从指数的编制规则入手。流动性差的股票会带来冲击成本,在进行指数复制时应优先选入流动性较好的股票。对于沪深300指数而言,因沪深300指数采用派许加权综合价格指数公式进行计算,计算公式如下:
1000调整市值
=∑(股价×A股总股本×加权比例)
其中加权比例是根据自由流通量和分级靠档计算的,代表着股票的流动性。也就是说,成份股分级靠档的加权比例越大,流动性越好,此股票带来的冲击成本越小,在进行指数跟踪时应该优先被选入。其他指数的编制规则与沪深300指数相类似,在进行指数跟踪的过程中应该找出代表流动性的指标,在挑选股票时优先选入流动性较好的股票。
综上所述,在进行指数跟踪时,应该同时考虑标的指数成份股之间的网络结构和各成份股的流动性。本文结合非负LASSO模型,以沪深300指数为标的指数进行实证分析,利用沪深300指数300只成份股的复杂网络和各成份股分级靠档的加权比例构建偏好权重,提出适用于沪深300指数跟踪的基于偏好变量的非负加权LASSO模型指数跟踪方法,此时的偏好变量是复杂网络中影响强度大的成份股和流动性强的成份股。Adaptive LASSO也是一种加权模型,但Adaptive LASSO的权重是通过OLS或是岭回归得到的,而本文提出新模型的权重是由股票关联网络和流动性决定的。实证结果表明,无论在样本内还是样本外,基于偏好变量的指数跟踪方法均优于基于非负LASSO的指数跟踪方法。
二、基于偏好变量的指数跟踪方法理论介绍
(一)偏好变量指标
考虑到偏好变量指标是由影响强度和“流动性”共同决定的,下文将分别介绍影响强度指标和流动性指标的选取和计算,再介绍偏好变量指标的构建。

因为影响强度的量化是通过构建成份股复杂网络实现的,下面以成份股公司为节点,给出构建复杂网络的基本步骤和无标度网络的判断[13-14]:
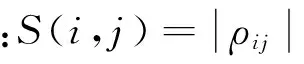

3) 记影响强度k的分布为p(k)。若k与p(k)之间的关系可以用一个幂函数近似地表示,即P(k)≈ck-γ,其中γ是幂律指数,c为常数,则称此网络具有无标度拓扑特性。选择一个合适的软阈值b,使在此软阈值下计算出来的影响强度分布的幂律特征尽量明显,此影响强度值就是最终的影响强度指标k=(k1,k2,…,kp)T。
影响强度表示节点公司的股票对其他公司股票价格影响的强度。在无标度网络中,影响强度大的节点数量不是很多,即通过选取少数几个影响强度大的成份股就可以达到较好的跟踪效果。在指数跟踪过程中,影响强度大的股票是被偏好的。


(二)基于偏好变量的指数跟踪方法
1.挑选股票。考虑到LASSO高维变量选择方法的稳定性和准确性[1],本文将对LASSO模型进行改进,使用改进的LASSO模型进行股票挑选,构建股票组合。
改进过程如下:首先,虽然从2006年8月证监会启动两融试点开始,A股市场开始引入了融券做空机制,尤其是2010年开通IF股指期货以来,中国股票市场正式存在做空机制,但是由于融券市场一直发展缓慢,尤其是2015年股灾以来,监管机构严禁裸空、严禁恶意做空,使做空受到极大限制,故在此背景之下,令回归参数非负是合理的[2-3],把参数非负的约束条件加入Tibshirani提出的基于线性回归的LASSO模型可得到非负LASSO模型,再把偏好变量作为权重加入非负LASSO模型可得到基于偏好变量的非负加权LASSO模型,此模型定义如下:
s.t.βj≥0;j=1,2,…,p
(1)
目标函数的第一项为残差平方和,使用的是最小二乘法。第二部分为加权LASSO惩罚项,其中λ为非负调和参数,λ越小惩罚越小,被剔除掉的变量就越少;λ越大,被剔除的变量则越多。通过控制λ的大小决定被保留变量的个数。

本文结合LARS算法完成变量选择和参数估计[15],最终得出“基于偏好变量的非负加权LASSO模型LARS算法”,具体步骤如下:
1) 计算“偏好向量”指标:

3) 用适用于非负LASSO的LARS算法[2-3],求解以下非负LASSO模型:
s.t.βj≥0;j=1,2,…,p

虽然用此算法在挑选股票的同时也进行了参数估计,但估计出的参数之和一般是不等于1的,为了减少跟踪误差和方便实际操作,还需要对构建好的股票组合中每只股票的权重重新计算。在计算权重之前,先介绍跟踪效果的评价指标。
2.跟踪效果评价指标。跟踪偏离度(Tracking Difference)、平均超额收益率(Average Excess Return)和跟踪误差(Tracking Error)是衡量跟踪效果的三个重要指标。
1)跟踪偏离度。跟踪偏离度为跟踪投资组合净值收益率与标的指数收益率之差,计算方法如下:
(2)

2)平均超额收益率。跟踪偏离度的均值又称为平均超额收益率,定义如下:
(3)
3)跟踪误差。跟踪误差为跟踪投资组合净值收益率和其标的指数收益率之差的标准差,即跟踪偏离度的标准差,日跟踪误差计算方法如下:
(4)
其中mean(TD)为TDt,t=1,2,…,n的均值。年跟踪误差(AnnualTrackingError)的计算公式为:
(5)
3.确定股票组合中每只股票的权重。假设标的指数含有p只成份股,我们已经从p只成份股中挑选出了M只股票形成了一个股票组合,为了使跟踪的偏离程度最小,通常最小化其跟踪误差,接下来要做的是以日跟踪误差最小为目标确定每只成份股在股票组合中的权重,采用如下优化模型:
s.t.0≤ϖm≤1
(6)


到此为止,通过基于偏好变量的非负加权LASSO模型,从标的指数的p只成份股中挑选出了M只影响强度大且流动性好的股票,构成了一个股票组合;再通过优化算法确定了股票组合中每只股票的权重ϖ=(ϖ1,ϖ2,…,ϖM),这M只成份股及其权重ϖ就构成了追踪标的指数的最优投资组合,这个构建最优投资组合的过程称为基于偏好变量的指数跟踪方法(Prefered-variable-based Index Tracking,PIT )。为了进行对比分析,实证部分还将同时使用非负LASSO模型进行指数跟踪(Nonnegative Lasso,NL)。
三、实证分析
(一)数据来源
沪深300指数是由沪深A股中规模大、流动性好的具有代表性的300只股票组成,于2005年4月8日正式发布。本文数据采用2005年4月8日至2015年10月30日的沪深300指数及其成份股每日的日向前复权收盘价。数据集内沪深300指数的走势图如图1。图1中横轴为时间,纵轴为沪深300指数,波动较大的地方就是2007年至2009年的金融危机时期和2015年的股灾时期。
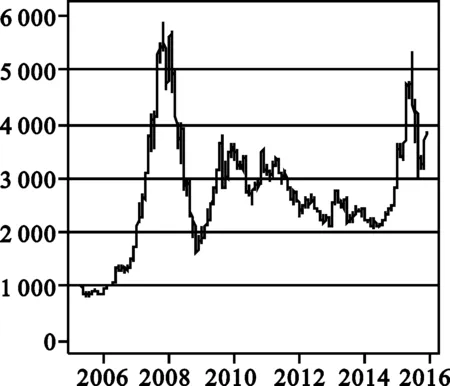
图1 沪深300指数走势图
按照时间顺序对数据集进行分割:6个月的数据作为样本内数据进行建模,1个月的数据作为样本外数据进行预测,这7个月的数据作为一个滚动数据集,原数据集生成了121个滚动数据集。本文所有数据均取自天软,所有结果均由R软件呈现。
(二)计算偏好变量指标
以第121号滚动数据集为例进行分析。
1.计算影响强度指标。先构建网络,再利用构建出的网络计算影响强度指标,具体步骤如下:
1)以沪深300指数的300个公司为节点,计算出样本内中300只股票对应的收益率xtj=rtj,t=1,2,…,n;j=1,2,…,300,计算xi与xj的相似性Sij=|ρij|,得到相似矩阵S。
2)为了构造出具有明显无标度拓扑特性的网络,分别计算软阈值b取1~20之间的整数时 影响强度k和k的分布p(k) ,用以比较不同软阈值下成份股网络的无标度特征。
3)若k与p(k)之间的关系为:
p(k)≈ck-γ
(7)
则称此网络具有无标度拓扑特性。为了判断是否具有无标度网络特性,对式(7)两边取对数,以log10p(k)为因变量,以log10k为自变量进行线性回归,线性回归的拟合优度R2可以用来量化无标度拓扑特征。很显然,R2越高,无标度拓扑特征越明显。图2绘出了软阈值与R2的关系。
从图2中可见,当软阈值大于12时,R2大部分达到了0.8以上,此时复杂网络的无标度拓扑特性较为明显。

图2 软阈值与R2的关系图
为了让每个节点的差异性更明显,本文在保证R2大于0.8的前提下选择使log10k系数估计值绝对值最大的软阈值17,这样构建的无标度网络会使影响强度大的节点更明显,以提高选取较大影响强度节点的效率。图3是软阈值取17时,影响强度k的直方图与无标度拓扑模型的拟合情况。

图3 k的直方图及无标度拓扑模型拟合情况图
图3左边是影响强度的直方图,可以看出幂律特性明显;右边是log10p(k)与log10k之间的关系,用来刻画幂律特征,即无标度特征,R2=0.88,斜率值为-1.55,说明P(k)≈ck-γ,γ=1.55,可以判定此复杂网络是无标度网络。用此网络计算出的影响强度k=(k1,k2,…,k300)T,将用来构建基于偏好变量的指数跟踪方法的权重。按同样的方法,对其他滚动数据集做同样的处理,求出121个滚动数据集的k。

3. 计算121个“偏好向量”指标:
(三)标的指数跟踪投资组合的构建
利用已经计算出来的偏好变量指标,使用基于偏好变量的指数跟踪方法,即PIT方法,在每个滚动数据集中的样本内数据中通过控制非负调和参数λ控制挑选出的股票数量,分别构建含有30、50、80只成份股的最优投资组合,再利用得到的投资组合在样本内和样本外中进行跟踪效果的检验,并与NL方法进行对比分析。
(四)指数跟踪效果对比
1.跟踪偏离度(TD)的对比分析。先来观察NL和PIT两种方法在第121个数据集中的跟踪偏离度的情况,图4为使用两种方法得到的跟踪偏离度的核密度图,从左往右分别是成份股数量为30、50、80的投资组合股票的跟踪偏离度的核密度图。

图4 跟踪偏离度的核密度图
从图4中可以看出:
1)两种方法在成份股数量变化时,出现跟踪偏离度为0次数较多,说明二者跟踪效果均良好。
2)在三张图中,对比NL方法,PIT方法的核密度图均呈现出尖峰但不厚尾的特征,且均值几乎为0,说明PIT方法得到的跟踪偏离度为0的概率比NL方法的要大很多,跟踪偏离度为0意味着没有误差,跟踪偏离度为0的概率越大越好,即PIT优于NL。
3)从左往右,投资组合的股票数量越来越多,跟踪偏离度为0的概率越来越大,说明在一定的条件下投资组合的股票数量越多,跟踪效果越好。
2.平均超额收益率(AER)的对比分析。为了更好地看出在整个数据集上两种方法在AER上的表现,图5绘出了所有滚动数据集的每一个跟踪投资组合的AER,横轴为滚动数据集的序号,纵轴为AER。

图5 平均超额收益率对比分析图
图5上面三幅图为121个滚动数据集样本内的AER对比分析,从左往右分别为含有30、50、80只成份股的跟踪投资组合在样本内中的AER表现。从这三幅图中可以看出,三种投资组合在样本内中PIT方法得到的AER在0附近的集中程度更高,NL偏离0的点更多,由于指数跟踪的目的是要紧贴标的指数,所以AER越接近于0越好,即PIT优于NL;下面三幅图为样本外的AER对比分析。总体上样本外的AER表现要比样本内的差一些,但两种方法的AER也基本上是在0附近,跟踪效果均还不错,并且与样本内中的结论一致的是PIT方法得出的AER仍然较NL方法得出的AER更优。在AER的表现上,NL和PIT方法均表现良好,且PIT优于NL。
3.年跟踪误差(ATE)对比分析。图6是两种方法在121个滚动数据集上进行指数跟踪时产生的跟踪误差的汇总,横轴为滚动数据集的序号,纵轴为ATE。

图6 年跟踪误差对比分析图
图6上部分三幅图为样本内的ATE对比分析,当选30只成份股时(左图),PIT方法产生的年跟踪误差控制在5.7%~1.6%之间,而NL方法产生的年跟踪误差多处超过了6%,此时PIT方法更优;当选50只成份股时(中图),PIT方法把跟踪误差控制在了3.6%~0.9%之间, NL方法产生的跟踪误差曲线总是高于PIT方法,且最大跟踪误差达到了5.3%,此时NL方法也的确不如PIT方法;提高成份股数量时,两种方法产生的跟踪误差都明显减小,成份股数量为80只时(右图),PIT的ATE取值范围为0.3%~1.9%,已经远远低于市场上的指数基金给出的年跟踪误差。市场上的指数基金的年跟踪误差一般在2%~3%之间,华夏沪深300ETF给出的年跟踪误差不超过2%,嘉实沪深300ETF约定日均跟踪误差不超过0.2%(换算成年跟踪误差为3%),当然此时NL方法跟踪误差也很小,其取值范围为0.4%~3%,但仍然不如 PIT。从样本内中的表现来看,PIT方法比NL和市场上的指数基金都要更优。
图6下部分三幅图为样本外。两种方法在样本外中的表现比样本内要差一些,尤其在滚动数据集的序号为19的附近样本外的跟踪误差更加不理想,其原因是序号为19的滚动数据集的样本外数据时间段为2007年4月2日至2007年4月30日,由美国次贷危机引起的全球金融危机影响了整个股市的正常运行,不管哪种方法在金融危机期间的追踪效果都不是很好;还有一个跟踪效果不理想的时间段就是2015年,影响原因是2015年的股灾。如若剔除金融危机时期和股灾时期,当选择30只成份股时,PIT方法的跟踪误差明显低于NL方法, PIT方法在多个时间段里产生了低于3%的ATE;选择50只股票时,PIT方法的ATE均控制在了6%以内,甚至在市场良好时ATE最小达到了2%以内,而NL方法却有很多高于了6%;当股票数量达到80只时,PIT方法的ATE已经控制在2%~3%之间了,虽然没有样本内中的ATE表现好,但大部分ATE也已经小于2%了,而NL方法基本上没有小于2%的时间段。从样本外的表现来看, PIT方法明显优于NL方法,且只要金融市场稳定,其ATE在成份股取到80只左右就可以达到市场上的指数基金的要求。
为了更细致地观察两种方法在金融市场稳定时的表现,将用表格的形式展示两种方法ATE的情况。因篇幅有限,此处仅展示11个滚动数据集的跟踪结果。表1为在第63个滚动数据集样本内(即2010年6月1日至2010年11月30日)至第73个滚动数据集样本内(即2011年4月1日至2011年9月30日)中两种方法的表现;表2为在第63个滚动数据集样本外(即2010年12月1日至2010年12月31日)至第73个滚动数据集样本外(即2011年10月10日至2011年10月31日)中两种方法的表现。选取这11个数据集的原因有两个:一是这个时间段的金融市场较为稳定;二是此时间段与Iam Wu展示NL方法跟踪效果选取的时间段相同,方便比较。
从表1和表2显示的结果来看,此时间段NL方法选择30只成份股的年跟踪误差控制在了2.84%~6.88%之间,这个结果与Iam Wu的研究结论是基本一致的,而PIT方法的年跟踪误差控制在了1.97%~5.94%之间,比NL的年跟踪误差小了很多。当选择50只成份股时,NL方法把年跟踪误差大部分控制在了5%以内,PIT把年跟踪误差大部分控制在了4%以内;当成份股数量达到80只时,两种方法都将跟踪误差控制在了3%以内,但PIT在样本内中将所有的跟踪误差都控制在了0.71%以内,而NL方法出现了超过1%的跟踪误差,样本外中PIT方法的ATE在1.33%~3.32%之间,而NL方法在1.99%~3.42%之间, PIT方法仍然优于NL。
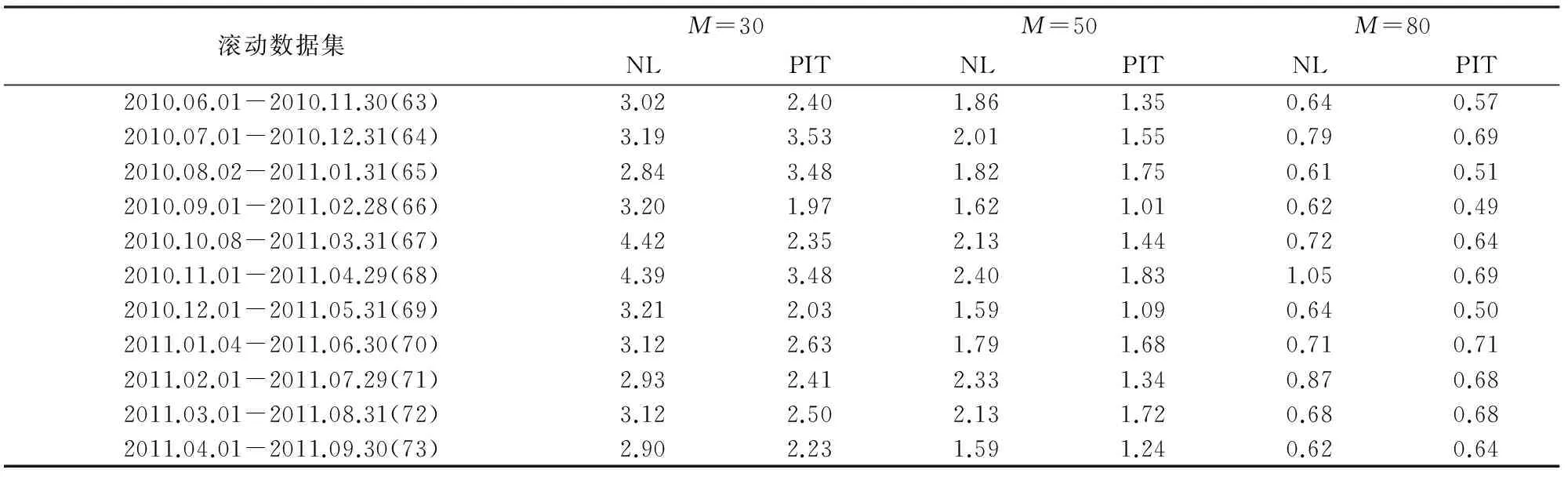
表1 样本内滚动跟踪结果对比表 单位:%

表2 样本外滚动跟踪结果对比表 单位:%
注:滚动数据集是用时间段来表示的,括号里面是滚动数据集的序号。
值得一提的是,当金融市场较为稳定时,不管是样本内还是样本外,PIT选择80只左右的成份股就能将跟踪误差控制在3%以内,这个数量比市场上大部分指数基金选择的成份股数量都要少很多,选择的成份股越少管理费用和交易费用就越少,冲击成本就越小,获得的投资收益就越多。
综上所述,无论是跟踪偏离度、平均超额收益率还是年跟踪误差,基于偏好变量的指数跟踪方法均优于基于非负LASSO的指数跟踪方法,并且两种方法在股票组合数量增加时,跟踪误差跟着减小。市场稳定时,当成份股数量达到80只以上,PIT方法的年跟踪误差可以控制在3%以内,NL方法需要100只以上才能达到这个标准。
四、结 论
考虑到指数跟踪不仅是指数化投资的技术关键,也是股指期货期现套利的关键,其重要性随着中国金融市场的逐渐完善日益增加。LASSO是大数据技术中用来处理高维变量问题的关键模型,使用非负LASSO进行指数跟踪是已有文献在考虑了中国市场上存在着卖空限制之后提出的一种新的指数跟踪模型,相关文献已经证实了非负LASSO指数跟踪方法优于传统的分层抽样方法。Adaptive LASSO是一种自适应加权模型,同样也有学者用此模型进行指数跟踪,也取得了良好的效果。
虽然直接使用非负LASSO或是Adaptive LASSO模型进行指数跟踪为指数跟踪技术提供了新的有效的方法,但是过于生硬,未考虑到金融市场的特殊性。本文考虑到在使用LASSO类方法进行指数跟踪时,应结合股票市场的结构和指数的编制方法这些专业领域的知识,对于一些有重要影响作用和流动性较好的变量优先选取,所以提出了基于偏好变量的指数跟踪方法,并使用了三个评估指数跟踪效果最常用的指标,即跟踪偏离度、平均超额收益和(年)跟踪误差对新方法进行了评估。实证结果显示,无论是样本内还是样本外,无论投资组合的成份股数量是30、50还是80只,新方法都稳稳地优于非负LASSO,并且当金融市场相对稳定时,只要成份股数量达到80只以上,新方法就可以达到市场上指数基金的跟踪误差标准,况且这个成份股数量远远小于市场上的大多数指数基金。
[1]Tibshirani R.Regression Shrinkage and Selection Via the LASSO[J].Journal of the Royal Statistical Society,Series B,1996,58(1).
[2]梁斌,陈敏,缪柏其,黄意球,陈钊.基于LARS-LASSO的指数跟踪及其在股指期货套利策略中的应用[J].数理统计与管理,2011(6).
[3]Lan Wu,Yuehan Yang,Hanzhong Liu.Nonnegative-LASSO and Application in Index Tracking[J].Computational Statistics and Data Analysis,2014,70(2).
[4]马景义,肖佳宁.含景气参数的非负lasso改进算法及其在指数跟踪中的应用[J].统计与信息论坛,2015(7).
[5] Zou H.The Adaptive Lasso and Its Oracle Properties[J].Journal of the American Statistical Association,2006(476).
[6]刘睿智,周勇.指数跟踪投资组合与多信息下指数可预测性[J].系统工程,2015,33(4).
[7]Kim H J,Kim I M. Scale-free Network in Stock Markets[J].Journal of Korean Physical Society, 2002(6).
[8] Barabási A-L,Albert R.Emergence of Scaling in Random Network[J].Science,1999(5439).
[9]Benjamin M T,Thiago R S,Daniel O C.Topological Properties of Stock Market Networks:The Case of Brazil[J].Physical A,2010,389(16).
[10]黄玮强,庄新田,姚爽.中国股票关联网络拓扑性质与聚类结构分析[J].管理科学,2008(3).
[11]Liu J, Huang J, Ma S. Incorporating Network Structure in Integrative Analysis of Cancer Prognosis Data[J]. Genet Epidemiol,2013(2).
[12]Zhang B, Horvath S.A General Framework for Weighted Gene co-Expression Network Analysis[J]. Statistical Applications in Genetics and Molecular Biology, 2005(1).
[13]Ovidiu D Iancu,Alexandre Colville,Denesa Oberbeck,et al.Cosplicing Network Analysis of Mammalian Brain RNA-Seq Data Utilizing WGCNA and Mantel Correlations[J].Frontiers in Genetics,2015(6).
[14]阎春宁,山石,史定华. 无标度网络的不同定义和包含关系[J].复杂系统与复杂性科学, 2014(2).
[15]Efron B,Hastie T,Johnstone I,Tibshirani R. Least Angle Regression[J].Annals of Statistics,2004,32(2).
(责任编辑:郭诗梦)
Prefered-variable-based Index Tracking
WANG Na, QIAN Zheng-ming
(School of Economics, Xiamen University, Xiamen 361005, China)
This paper proposes the prefered-variable-based index tracking after considering the network structure of stock market and index methodology which tell us the stock with great infulence-strength and good liquidity should be prefered. Then we applied this method in tracking CSI 300 stock index and evaluated new method from tracking difference, average excess return and annual tracking error,and compared it with nonnegative-LASSO.The empirical results show that this method performs better than nonnegative-LASSO and most of index funds in the market.
scale-free network; influence-strength;liquidity; index tracking
2016-02-29;修复日期:2016-06-04
教育部重点研究基地重大项目《开放经济条件下资源环境约束强化、技术进步与中国经济增长效率》(12JJD790027)
王娜,女,江西吉安人,博士生,研究方向:统计学;
O212∶F830
A
1007-3116(2016)09-0009-08
钱争鸣,男,江苏泰兴人,经济学博士,教授,博士生导师,研究方向:统计学,数量经济学。

