铝合金板式节点网壳阻尼特性试验研究
郭小农, 王 丽, 相 阳, 熊 哲, 赵卫华, 严 勇
(1.同济大学 土木工程学院,上海 200092; 2.上海宝冶工程技术有限公司,上海 200941)
铝合金板式节点网壳阻尼特性试验研究
郭小农1, 王丽1, 相阳1, 熊哲1, 赵卫华2, 严勇2
(1.同济大学 土木工程学院,上海200092; 2.上海宝冶工程技术有限公司,上海200941)
为研究铝合金板式节点网壳结构阻尼特性,填补现行设计规范对铝合金结构阻尼比取值的空白,对一铝合金板式节点网壳的阻尼比进行了实测。采用锤击法对结构施加动力激励,由拾振器记录结构各点的加速度响应。通过FFT变换得出节点加速度响应频谱,采用半功率带宽法估算结构阻尼比。通过改变锤击力度、拾振器位置、敲击点位置,设计了57种工况,并测出一系列阻尼值;对所得数据进行统计分析,得出铝合金板式节点网壳阻尼比平均值,并建议此类结构阻尼比取为3.3%。运用该阻尼参数建立有限元模型,分析结构动力响应,结果表明:节点加速度响应实测曲线与有限元模型计算得到的响应曲线的峰值、周期和振动衰减规律均吻合较好,证明所测得阻尼值可为铝合金板式节点网壳的动力分析与工程设计提供依据。
铝合金网壳;板式节点;阻尼特性;半功率带宽法
铝合金板式节点网壳是最为常见的铝合金结构型式之一,此类结构在国外应用较早,已建成数千座。铝合金结构在我国的应用起步较晚,但近年来发展迅速,已建成上海科技馆[1]、上海辰山植物园[2]等工程。
对铝合金板式节点网壳的承载性能,国内外学者展开了研究并取得诸多成果。郭小农等[3]对14个铝合金板式节点试件进行静力加载试验,归纳出板式节点的破坏模式;对铝合金板式节点承载力进行理论分析,推导出在弯矩和轴力共同作用下节点板的块状拉剪承载力公式和中心区域局部屈曲公式[4];基于铝合金板式节点的弯矩-转角试验曲线,分析得到节点初始刚度计算公式[5],进而提出了考虑弯矩和轴力共同作用的弯曲刚度四折线模型[6]。曾银枝等[7]研究了铝合金穹顶网壳的力学性能,研究表明铝合金穹顶网壳力学模型与钢网壳类似,可用非线性空间梁单元建立结构的有限元计算模型。
当铝合金板式节点网壳结构承受地震作用、脉动风荷载以及各类冲击荷载时,需分析其动力响应。由于此类结构的材料性能[8]、节点刚度特性[9]、开口薄壁杆件受力变形特性等均明显区别于钢网壳结构,故对其实施动力响应分析时(尤其是结构承受强震、强风作用时[10~11]),存在一系列特殊问题亟待研究。其中,铝合金板式节点网壳结构的阻尼取值,应首先予以关注。我国的《铝合金结构设计规范》和《建筑抗震设计规范》对铝合金结构的阻尼比并没有规定,导致此类结构的动力分析和其工程抗震、抗风设计存在很大不便。由于结构阻尼是对结构振动过程中能量耗散速率的综合反映,故只能采用试验实测方法予以测量。
鉴于此,针对铝合金板式节点网壳的阻尼比进行实测。采用锤击法对结构施加动力激励,用拾振器记录结构各点的加速度响应。通过快速傅里叶变换(Fast Fourier Transforn,FFT)得出频谱,并采用半功率带宽法估算结构阻尼比。通过改变锤击力度、拾振器位置、敲击点位置,设计了57种工况,并测出一系列阻尼值。对所得数据进行统计分析,得出了铝合金板式节点网壳的阻尼比均值。运用该阻尼参数建立有限元模型,分析结构的动力响应,结果表明:节点加速度响应实测值与理论值均吻合较好。故本文得到的铝合金板式节点网壳阻尼值可为此类结构的动力响应分析与工程设计提供依据。
1 试验概况
1.1网壳结构
试验用铝合金板式节点网壳为Kiewitt-6型,径向5环,跨度8 m,矢高0.5 m。网壳共有杆件210根,采用挤压H铝型材制作,杆件截面为H100 mm×50 mm×4 mm×5 mm。网壳共有非支座节点61个,所有非支座节点均为板式节点,节点圆盘盖板的半径为100~114 mm不等,厚度均为5 mm。支座节点为固定铰支座。网壳所有构件和节点板材质均为6061-T6。
采用悬挂质量块的方式模拟铝合金板式节点网壳的节点质量。质量块布置在跨中节点及内部三环节点上(共37个),各质量块均为17 kg。
网壳模型见图1,板式节点形式见图2,网壳照片见图3。

图1 网壳模型Fig.1 Latticed shell modal
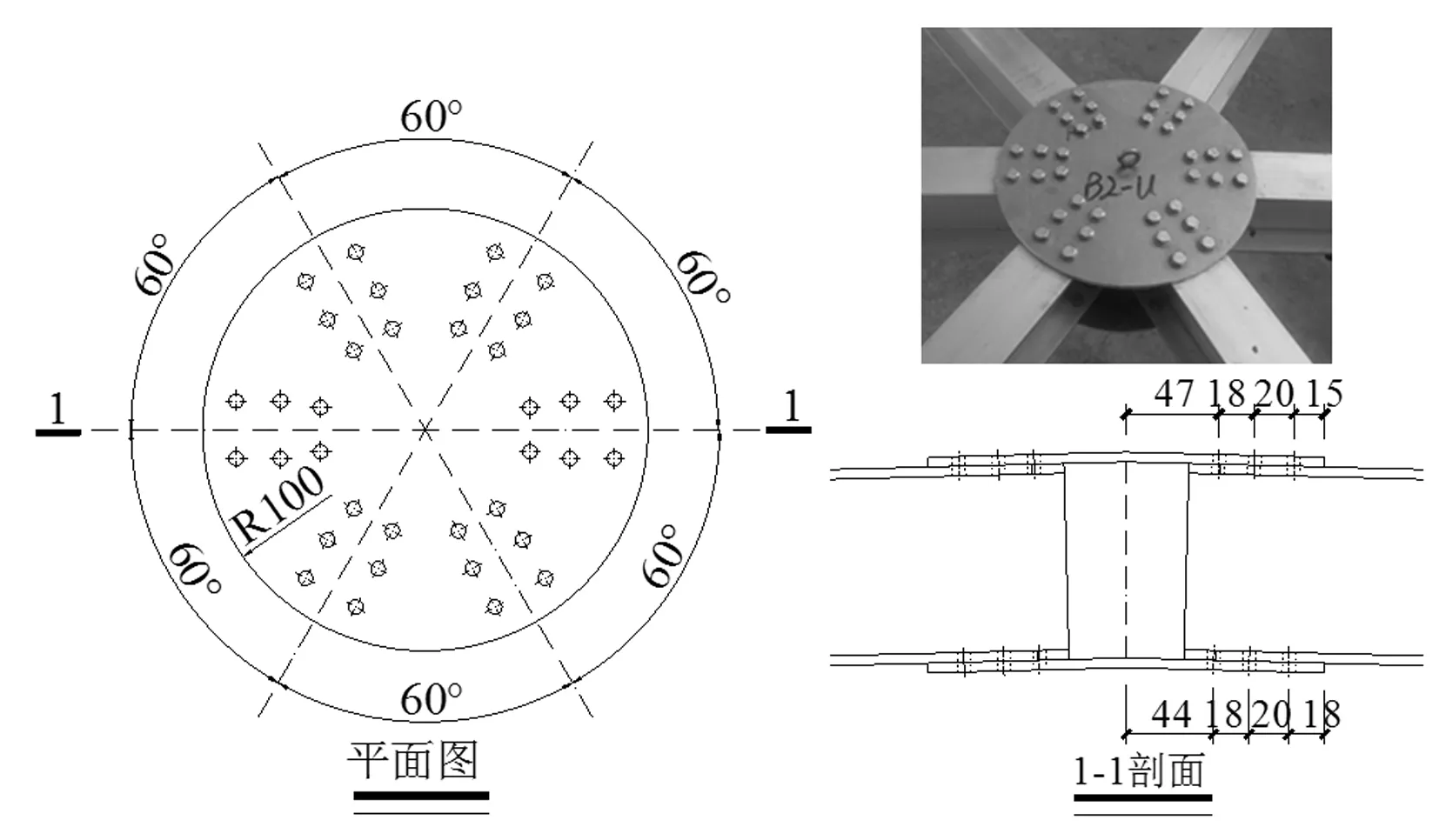
图2 铝合金板式节点Fig.2 Aluminum alloy gusset joints

图3 测试用铝合金网壳Fig.3 The aluminum alloy latticed shell used for the test
1.2测试方案
试验采用“锤击激励+拾振器采集”方式,对结构实施单点锤击、多点测量:锤击结构某节点,由多个竖向拾振器(该铝合金板式节点网壳矢跨比较小,故竖向振动为主)测量网壳各节点的振动衰减反应。采用INV3020 CPCI高性能采集仪进行数据采集,并由北京东方振动和噪声技术研究所生产的DASP V10软件进行信号处理及参数识别。
试验设计的4种锤击位置见图4,21种拾振器布置见图5,测试工况共计57种。每种工况采用如下规则编号:“K”表示敲击点布置,“S”代表拾振器布置:例如编号“K1-S04”代表敲击点在位置1,拾振器布置在位置04。同时,为研究敲击力度(动力激励幅值)对实测阻尼值的影响,还进行了“K1-S03*”试验,与“K1-S03”试验进行对比,“*”表示重度敲击。

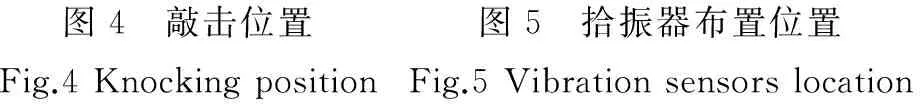
图4 敲击位置图5 拾振器布置位置Fig.4KnockingpositionFig.5Vibrationsensorslocation
2 试验数据及分析处理
2.1实测频率及阻尼比
根据结构加速度响应频谱图,可识别出对结构动力响应贡献较大的振型频率,采用半功率带宽法[12-13],计算得到各阶振型频率对应的结构阻尼比。各工况下,识别、计算得到的结构阻尼比(包括对应频率值)列于表1。
需注意的是,表1中f1、f2、f3表示测试识别到的频率序号,并不一定表示结构的前三阶自振频率。试验所用DASP V10信号处理软件只能跳跃识别部分频率,而且在频率密集的频段,所识别出的频率存在相互耦合,故表1中实测值可能是多个固有频率的耦合值。与有限元分析结果对比,第1阶振型频率实测值f1与第1阶振型频率理论值基本相符,而第2阶、第3阶频率实测值并不是网壳的第2阶、第3阶频率,而是更高阶振型频率。
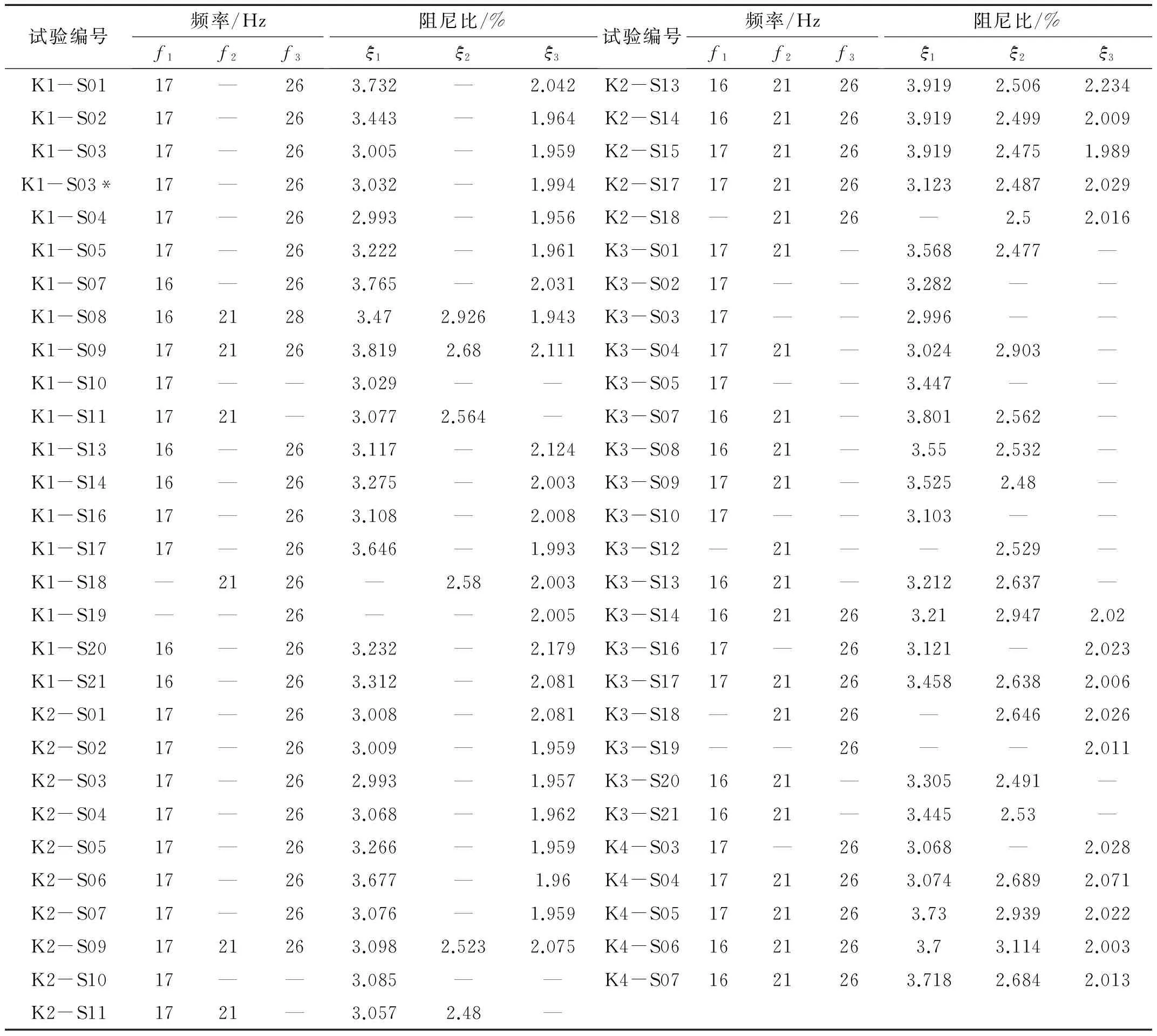
表1 各工况实测频率及其阻尼比
注:*表示重度敲击。
2.2数据分析及处理
2.2.1激励位置、拾振器布置对峰值响应频率的影响
图6给出了部分工况的加速度响应频谱图。由图6可知:加速度峰值所对应的频率值,较明显地受到敲击位置和拾振器位置的影响。建立有限元模型,计算结构自振频率和振型(详见本文第3节),并将结果与表2列出的各工况频谱图峰值对应频率进行对比,可知:
1) 当敲击网壳顶点时,K1-S10和K1-S13工况下的峰值频率均为17 Hz,此值与结构的第1阶自振频率值非常接近,这是因为拾振器位置较为接近第1阶振型的最大位移节点。
2) 对于K1-S01工况,其加速度响应峰值对应频率为26 Hz,此值与结构的第6阶自振频率非常接近,这是因为对第6阶模态,网壳跨中节点位移最大,而拾振器恰恰布置在这一位置。
3) K1-S10和K1-S13测得的频谱图几乎一致,其峰值频率均为17 Hz,体现了由于结构对称性而引起的重频特性。
4) K2-S07工况峰值加速度所对应的频率为所识别出的第2阶振型频率,其频率值与有限元模型分析得到的结构第8阶振型频率接近,这说明此工况下,7号拾振器对应节点动力响应主要由该阶振型控制;而在K2-S04工况中,节点动力响应则主要由基本振型控制。
5) 当敲击3号点时,K3-S10、K3-S16工况的频谱图中出现了3个峰值频率:其中第1个为16 Hz,接近结构第1阶频率,第3个峰值频率为36 Hz,接近结构第13阶频率,这表明对于位于网壳中部的第10号拾振器和位于网壳外圈的第16号拾振器,高阶振型对响应存在一定贡献。
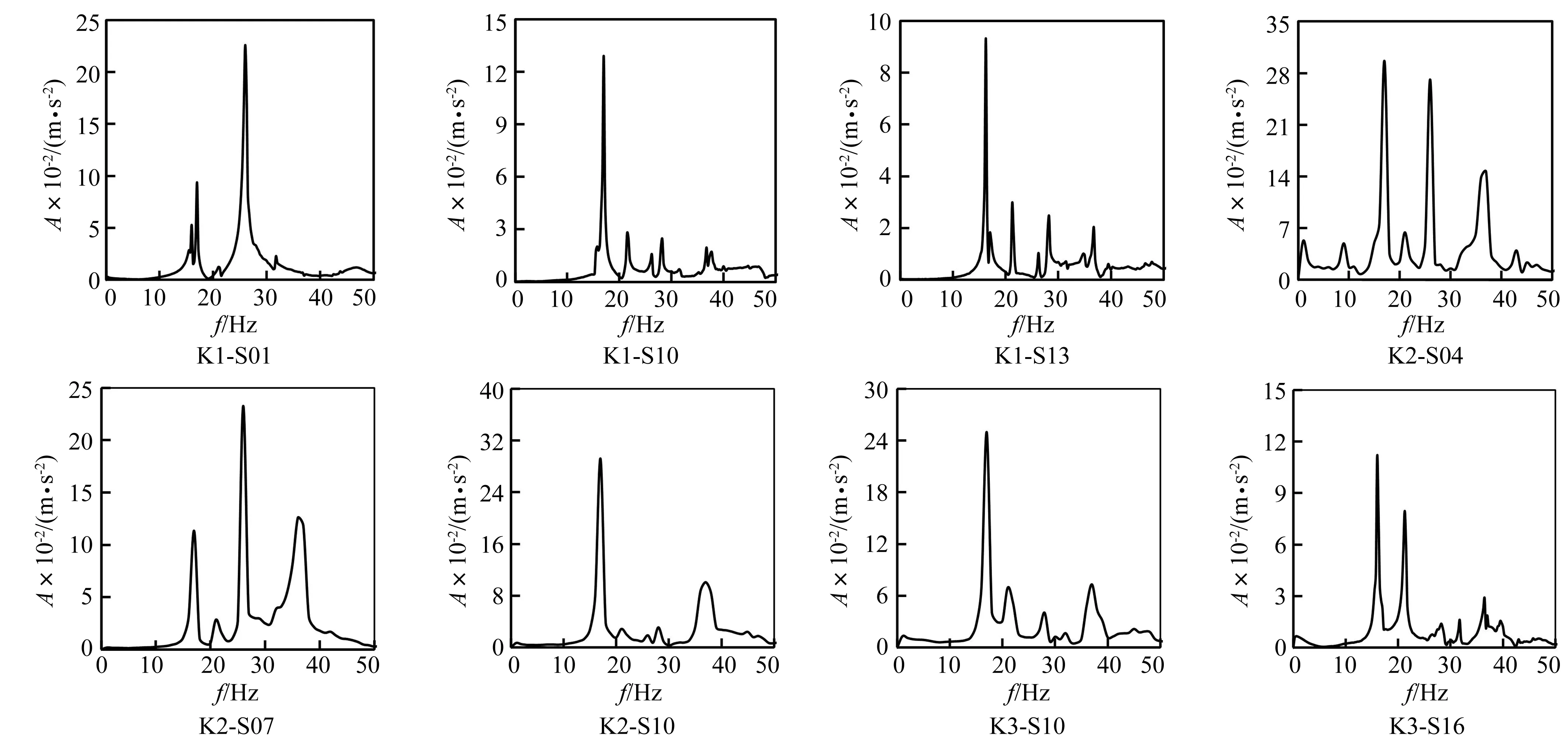
图6 部分工况节点加速度响应频谱图Fig.6 Frequency spectra of the nodal acceleration responses under some load cases
2.2.2激励幅值、激励位置对阻尼比的影响
工况K1-S03和K1-S03*比较了锤击力度对实测结果的影响,依表1的数值可得:轻击时结构的第1阶阻尼比为3.005%,而重击时为3.032%,二者误差仅为0.9%,这表明敲击力度对阻尼比实测结果影响甚微。
从表1还可知:敲击位置对于结构的实测阻尼比影响也较小。虽然敲击位置不同,激振出的频率略有不同(如K3-S09未测出26 Hz频率,而K2-S09有测出),但相同振型(实测频率相同或接近)所对应的阻尼比几乎无差异。
2.2.3阻尼值取值建议
阻尼比数值由半功率带宽法求得。结构第1阶振型实测阻尼比取值分布直方图如图7所示,其横轴为第1阶振型实测阻尼比取值范围,纵轴为实测阻尼比值落在相应范围内的试验工况数量。从图7可知,实测的结构低阶模态所对应的阻尼比大致在2.9%~3.9%之间。阻尼比是结构的固有特性,确定其标准值与设计准则无关,因而本文阻尼比数值取平均值3.33%,考虑到工程应用,铝合金板式节点网壳阻尼比值取整为ξ=3.3%。

图7 第一阶振型阻尼比实测值分布直方图Fig.7 Histogram of tested damping ratio value of vibration mode 1
相对于建筑钢结构(规范规定阻尼比ξ=0.02),铝合金板式节点网壳结构阻尼略大。原因在于钢结构多采用焊接连接(或栓焊组合连接),而铝合金板式节点网壳结构采用螺栓连接,这种连接的干摩擦耗能增加了结构阻尼。
将结构第1阶、第2阶、第3阶振型实测阻尼比平均值列于表2。由表2可见:结构振型阶数越高,所对应的阻尼比越小。现有研究认为:结构部件之间的干摩擦是阻尼的主要来源之一[14]。对于铝合金板式节点网壳结构,其低阶振型位移响应较大,结构内部部件之间摩擦滑移亦较大,故对应的能量耗散增加,宏观上则表现出较高的阻尼值。

表2 阻尼比平均值
3 有限元分析检验
3.1结构自振特性
首先采用有限元程序ANSYS计算得到结构的自振频率和振型。结构前10阶自振频率列于表3,前10阶振型见图8。从表3和图8可知,网壳模型第1阶和第2阶、第4阶和第5阶、第9阶和第10阶振型为重频振型,其振型形态两两相同。

表3 结构前10阶自振频率(有限元模型)

图8 结构前10阶振型Fig.8 The former 10 natural vibration mode of the structure
3.2加速度响应对比
有限元数值模型采用Rayleigh阻尼考虑结构的阻尼特性,Rayleigh阻尼系数可根据实测阻尼比反算得到:

(1)
式中:ωi、ωj为任意给定的两阶固有频率;ξi、ξj为对应的两阶阻尼比。
选取1种典型工况(K3-S04),将实测节点加速度响应与有限元数值分析结果进行对比,以验证本文建议阻尼比取值的合理性。有限元数值模型中,结构的阻尼比采用下列两种方式确定:
1) 根据K3-S04的频谱图,得到结构前2个加速度响应频谱峰值对应的阻尼比(ξ1=3.005%和ξ2=1.959%),依据式(1)得α1= 0.664 819,β1=0.001 257。将α1、β1值输入有限元模型,算得节点加速度响应时程,命名为Analysis-01。
2) 结构各阶振型阻尼比均取建议值,即3.3%,依据式(1)得α2= 0.620 053,β2= 0.001 737。将α2、β2值输入有限元模型,算得节点加速度响应时程,命名为Analysis-02。
将实测节点加速度时程响应曲线、采用上述“1)”、“2)”阻尼方案算得的节点加速度时程响应曲线绘于图9。图中曲线为与拾振器04位置相同的节点加速度响应时程曲线。由图9可知,在0~0.3 s内,加速度响应实测曲线和有限元分析所得响应曲线的峰值、周期和振动衰减规律均符合较好。
工程应用中,一般用一个固定阻尼比,替代各阶振型阻尼比。图9分析结果表明:依据“1)”、“2)”两种阻尼方案,计算得到的节点加速度响应曲线接近重合,说明使用固定阻尼值(ξ=3.3%),即可求得满足工程要求的结构响应。因此,本文给出的铝合金板式节点网壳结构阻尼比建议值是适用的。

图9 节点加速度响应曲线Fig.9 The acceleration response curves
4 结 论
本文以铝合金板式节点网壳结构为研究对象,采用锤击法对结构施加动力激励,用拾振器记录结构各点的加速度响应,通过快速傅里叶变换得出节点加速度相应频谱,最后并采用半功率带宽法估算得出结构的阻尼比。研究所得主要结论如下:
(1) 加速度响应频谱峰值所对应的频率值,受到激励位置和拾振器位置的影响,但激励位置、激励幅值和拾振器位置对阻尼比实测结果影响均较小。
(2) 结构振型阶数越高,所对应的阻尼比越小。结合本文试验结果,偏于安全地,建议取铝合金板式节点网壳结构阻尼比ξ=3.3%。运用该阻尼比建立的有限元模型,节点动力响应计算值与实测值吻合较好。
本文给出的铝合金板式节点网壳阻尼值可为此类结构的动力响应分析与工程设计提供依据。由于铝合金结构普遍采用螺栓连接,故本文针对板式节点网壳结构的研究结论亦可为其他类型铝合金结构阻尼比取值提供参考。
[1] 沈祖炎, 郭小农, 李元齐. 铝合金结构研究现状简述[J]. 建筑结构学报, 2008, 28(6): 100-109.
SHEN Zuyan, GUO Xiaonong, LI Yuanqi. State-of-the-arts of research on aluminum alloy structures [J]. Journal of Building Structures, 2008, 28(6): 100-109.
[2] 郭小农. 铝合金结构构件理论和试验研究[D].上海:同济大学,2006.
[3] 郭小农, 熊哲, 罗永峰, 等. 铝合金板式节点承载性能试验研究[J]. 同济大学学报(自然科学版), 2014, 42(7): 1024-1030.
GUO Xiaonong, XIONG Zhe, LUO Yongfeng, et al. Experimental research on the load-bearing behavior of aluminum alloy ausset joint[J]. Journal of Tongji University:(Natural Science), 2014, 42(7): 1024-1030.
[4] 郭小农, 熊哲, 罗永峰, 等. 铝合金板式节点承载力设计方法及构造要求[J]. 同济大学学报(自然科学版), 2015, 43(1): 47-53.
GUO Xiaonong, XIONG Zhe, LUO Yongfeng, et al. The design method and detaied requirements of bearing capacity of aluminum alloy gusset joint[J]. Journal of Tongji University(Natural Science), 2015, 43(1): 47-53.
[5] 郭小农, 熊哲, 罗永峰, 等. 铝合金板式节点初始刚度[J]. 同济大学学报(自然科学版), 2014, 42(8): 1161-1166.
GUO Xiaonong, XIONG Zhe, LUO Yongfeng, et al. Initial bending stiffness of aluminum alloy gusset joint[J]. Journal of Tongji University(Natural Science),2014,42(8): 1161-1166.
[6] 郭小农, 熊哲, 罗永峰, 等. 铝合金板式节点弯曲刚度理论分析[J]. 建筑结构学报, 2014, 35(10): 144-150.
GUO Xiaonong, XIONG Zhe, LUO Yongfeng, et al. Theoretical study on bending stiffness of aluminum alloy gusset joint[J]. Journal of Building Engineering,2014,35(10): 144-150.
[7] 曾银枝, 钱若军, 王人鹏, 等. 铝合金穹顶的试验研究[J]. 空间结构, 2005, 6(4): 47-52.
ZENG Yinzhi, QIAN Ruojun, WANG Renpeng, et al. Test research on the aluminous-alloy dome[J]. Spatial Structures,2005, 6(4): 47-52.
[8] 郭小农, 沈祖炎, 李元齐, 等. 国产结构用铝合金材料本构关系及物理力学性能研究[J]. 建筑结构学报, 2008, 28(6): 110-117.
GUO Xiaonong, SHEN Zuyan, LI Yuanqi, et al. Stress-strain relationship and physical-mechanical properties of domestic structural aluminum alloy [J]. Journal of Building Structures, 2008, 28(6): 110-117.
[9] 郭小农, 熊哲, 罗永峰, 等. 铝合金板式节点面外初始弯曲刚度的杆件间交互影响[J]. 湖南大学学报(自然科学版), 2015, 42(3): 36-42.
GUO Xiaonong, XIONG Zhe, LUO Yongfeng, et al. The out-of-plane initial bending stiffness interaction of members on the aluminum alloy gusset joint[J]. Journal of Hunan University(Natural Sciences), 2015, 42(3): 36-42.
[10] ZHI X, FAN F, SHEN S. Elasto-plastic instability of single-layer reticulated shells under dynamic actions[J]. Thin-Walled Structures, 2010, 48(10): 837-845.
[11] 范峰, 支旭东, 沈世钊. 网壳结构强震失效机理[M]. 北京: 科学出版社, 2014.
[12] 陈奎孚, 张森文. 半功率点法估计阻尼的一种改进[J]. 振动工程学报, 2002, 15(2): 151-155.
CHEN Kuifu, ZHANG Senwen. Improvement on the damping estimation by haly powerpoint method[J]. Journal of Vibration Engineering, 2002, 15(2): 151-155.
[13] 应怀樵, 刘进明, 沈松. 半功率带宽法与 INV 阻尼计法求阻尼比的研究[J]. 噪声与振动控制, 2006,26(2):4-6.
YING Huaiqiao, LIU Jinming, SHEN Song. Half-power bandwidth method and INV damping ration solver study[J]. Noise and vibration control, 2006, 26(2): 4-6.
[14] 董军, 邓洪洲. 结构动力分析阻尼模型研究[J]. 世界地震工程, 2000, 16(4): 63-69.
DONG Jun, DENG Hongzhou. Studies on the damping modeling for structural dynamic time history analysis[J]. World Information on Earthquake Engineering,2000,16(4): 63-69.
Experimental study on the damping property of aluminum alloy latticed shells with gusset joints
GUO Xiaonong1, WANG Li1, XIANG Yang1, XIONG Zhe1, ZHAO Weihua2, YAN Yong2
(1. College of Civil Engineering, Tongji University, Shanghai 200092, China;2. Shanghai Baoye Engineering Technology Corp., Ltd., Shanghai 200941, China)
In order to investigate the damping property of aluminum alloy latticed shells with gusset joints, as well as to fill a blank in the existing design codes which do not give clear damping ratio value of this kind of structures, experimental tests were carried out on an aluminum alloy latticed shell with gusset joints. The structural dynamic responses were aroused by hammer impact, and were recorded by vibration sensors. The acceleration response frequency spectra at nodes were obtained through FFT method, and the structural damping ratio was calculated by half-power bandwidth method. In the experiments, the different strength of hummer impact, different locations of vibration sensors and different excitation places were considered, a total number of 57 test load cases were designed and executed, and a series of damping ratios were gotten from the experiments. A statistic study was carried out on the data given by the tests, then an average damping ratio was suggested for this kind of structures, that is,ξ=3.3%. A finite element model of the tested structure was established using the suggested damping ratio, and the nodal dynamic responses given by numerical analysis show good consistency with those given by the tests. It is demonstrated that the damping ratio given in the paper could serve the purpose of the dynamic response analysis and engineer design of aluminum alloy latticed shells with gusset joints.
aluminum alloy latticed shell; gusset joints; damping property; half-power bandwidth method
国家自然科学基金项目(51478335)
2015-08-19修改稿收到日期:2015-10-12
郭小农 男,博士,副教授,1977年生
相阳 男,博士生,1988年生
E-mail:001_xiangyang@tongji.edu.cn
TU395
A DOI:10.13465/j.cnki.jvs.2016.14.006

