微细立铣刀动力学分析的Chebyshev谱方法

黄意新， 尹青峰， 赵　阳

(1.哈尔滨工业大学 航天学院，哈尔滨　150001； 2. 中国工程物理研究院 机械制造工艺研究所，四川 绵阳　621900)



微细立铣刀动力学分析的Chebyshev谱方法

黄意新1， 尹青峰2， 赵阳1

(1.哈尔滨工业大学 航天学院，哈尔滨150001； 2. 中国工程物理研究院 机械制造工艺研究所，四川 绵阳621900)

采用 Chebyshev 谱方法对微细立铣刀动力学特性进行研究。考虑刀具剪切变形与转动惯量效应，建立刀具各段均匀或变截面 Timoshenko 梁动力学模型，利用 Chebyshev谱方法对动力学方程进行离散，通过动态子结构法综合得到刀具整体动力学模型，编制了刀具动力学特性分析软件;仿真得到了微细立铣刀固有频率及模态振型并与分段阶梯梁方法及有限元方法进行了比较，验证了方法的可行性;研究了刀柄长度、刀颈半锥角及刀头长径比等刀具结构参数对刀具固有频率的影响。算例的数值计算结果表明：当 Chebyshev 多项式阶数>16时，前四阶计算结果偏差收敛至 0.04% 内，计算精度较高;该方法可用于微细立铣刀参数优化设计。

微细立铣刀；切比雪夫谱方法；动力学特性；动态子结构法

微铣削是加工微小零件和高精密零件的一种新型加工技术[1]，是微细加工研究领域中，由电加工跨入非电加工、硅微工艺跨入非硅工艺、二维加工跨入三维加工的一项重要的先进制造技术[2]，在制造航空航天等领域所用的三维复杂微结构零件方面具有明显优势[3]。由于加工尺度的缩小，微细铣削刀具尺寸小、刚性弱，加工质量与稳定性对刀具性能敏感[4-5]，刀具结构参数将影响刀具动力学特性进而影响加工过程中的刀具动态响应[6]。

目前用于铣刀动力学分析的模型主要有：整体悬臂梁模型、分段阶梯梁模型及有限元模型等[7]。张俊等[8]基于等质量、等截面积以及等刚度的原则将刀齿等效为均匀直径梁，主要用于快速获取铣刀频响特性。方泽平等[9-11]应用分段思想建立微细铣刀悬伸部分的动力学模型，将刀具分为三部分，刀柄、刀头部分为等截面圆柱梁，刀径部分则简化为等梯度变化的阶梯梁，分析了刀具结构参数对刀具动力学特性的影响。YANG等[12-13]将铣刀分为：装夹段、悬伸段及刀刃段三部分，采用 Euler-Bernoulli 梁和 Timoshenko梁理论建立了铣刀动力学模型用于刀尖频响函数分析。MUSTAPHA等[14]应用广义Hamilton变分原理推导了微细铣刀动力学模型，采用谱元法计算了刀具固有频率随刀具结构参数的变化规律。谱方法是继差分法和有限元法之后又一种重要的数值方法，它用在整个区间都非零的连续函数的线性组合来逼近精确解，其精度可直接由级数展开式的项数来决定，具有指数收敛特性，常被视为具有“无穷阶”收敛性，当真解足够光滑时，采用谱方法可以得到很好的效果。谱方法可应用于微分方程数值求解[15]，梁动力学问题分析等[16]。从函数近似的角度看，谱方法可以分为Fourier方法，Chebyshev或Legendre方法。前者适用于周期性问题，后者适用于非周期性问题[17-18]。

为获得微细立铣刀的精确动力学特性，基于Timoshenko梁理论，采用Chebyshev谱方法及动态子结构法建立微细铣刀的变截面Timoshenko梁动力学模型，分析刀具结构参数对刀具动力学特性的影响，为微细铣刀结构优化设计提供参考。

1　微细立铣刀结构动力学模型

微细立铣刀见图1(a) ，包括刀柄、刀颈、刀头三部分，并可简化为图1(b)的变截面悬臂梁模型。刀柄为直径d1，长L1的均匀圆柱梁；刀颈为半锥角φ的锥形梁，其长为L2；刀头为直径d3，长L3的均匀圆柱梁。由于截面非均匀，应用动态子结构法，将刀具分为(1)、(2)、(3) 三个子结构，①、④为边界，②、③为子结构交界面。首先获得子结构运动方程，再根据边界条件、子结构交界面的位移和力的协调条件，将离散的子结构运动方程组装成整体结构运动方程并计算其动力学特性。

图1　微细立铣刀及其几何模型Fig.1　Micro-endmill and its geometric model

对于子结构 (2)，变截面Timoshenko梁运动方程为：

(1)

式中：κ为剪切系数;G为材料剪切模量;E为材料杨氏模量;横截面积A=A(x)、惯性矩I=I(x)沿轴向发生变化。令：χ=ρ/κG，σ=E/κG，F=-f/κG，Ψ=-ψ/κG，式 (1) 可表示为：

(2)

对于子结构(1)、(3)，横截面积A、惯性矩I为常数，运动方程式(2)可表示为：

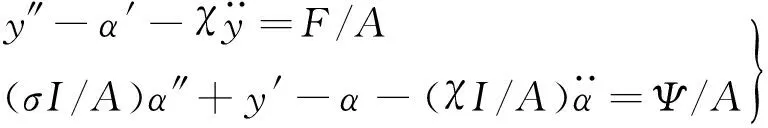
(3)

2　Chebyshev 谱方法

2.1Chebyshev多项式理论

文献 [19] 给出了Chebyshev谱方法理论的详细论述。此处给出Chebyshev多项式逼近函数及其导数以及函数内积的方法，作为推导Timoshenko梁离散运动方程的基础。第一类Chebyshev多项式是一类递归正交多项式，其第k项可表示为：

Tk(x)=cos(karccosx)

(4)

式中：k为非负整数，多项式满足递推关系：

Tk(x)=2xTk-1(x)-Tk-2(x)

(5)

式中：x∈[-1,1]。Chebyshev也可以定义在其它区间范围，如l∈[0,L]，需对l进行变换x(l)=(2l-L)/L。函数y(x)的N-1阶Chebyshev多项式逼近为：

(6)

式中:ak为多项式系数，组成N维系数向量a，采用Gauss-Lobattoe采样点xk=cos((k-1)π/(N-1))，k=1,2,…,N，插值点函数值yN(xk)组成N维函数值向量y，则有：

y=ΓBa

(7)

式中：ΓB为函数值向量与多项式系数向量间的变换矩阵，在已知N个采样点及其函数值时可求得系数向量a，进而可以获得函数y(x)在任意点的函数值，由式(7)可得：

(8)

Chebyshev多项式导数：

T0′(x)=0,T1′(x)=T0(x),

T2′(x)=4T1(x)

(9)

(10)

(11)

上述各式中k为大于1的正整数，由式(6)、式(9)、式(10)、式(11)可得函数y(x)导数的N阶Chebyshev多项式逼近：

(12)

多项式系数bk构成N维系数向量b:

b=Da

(13)

式中：D可由式(10)、式(11)、式(13)获得:

(14)

综合式 (8)、式(12)可得函数y(x)的N阶导数值向量：

(15)

由式 (6)、式(7)、式 (15)可知，在已知函数y(x)N个采样点上函数值的情况下，可以采用Chebyshev多项式逼近y(x)的各阶导数值。

Chebyshev多项式积分：

(16)

式中：n为正整数，由式(6)、式(16)可得：

(17)

式中：v为含N维列向量，称作Chebyshev积分向量，其元素可由式 (16) 得到。

函数内积采用Chebyshev多项式逼近可表示为：

(18)

V、Vh为N×NChebyshev内积矩阵。

由Chebyshev多项式理论可知，在已知函数N个采样点函数值时，可以采用Chebyshev多项式逼近函数及其各阶导数或积分值，计算其与其它函数的内积。

2.2Timoshenko梁离散运动方程

对于子结构 (2)，采用N阶Chebyshev多项式逼近其运动方程式(2) 的解：y=y(x,t)，α=α(x,t):

(19)

由于有限项Chebyshev多项式逼近函数时存在截断误差，不能精确满足微分方程式(2)，将产生残差：

(20)

则方程式(2)的等效积分形式为：

(21)

式中：θ1(x)、θ1(x)为权函数，采用Galerkin加权余量法，θ1(x)、θ1(x)亦为Chebyshev多项式，设x为Gauss-Lobattoe节点向量，y、α分别为函数y=y(x,t)、α=α(x,t)某时刻在节点处的函数值向量，A、I分别为A(x)、I(x)的在节点处的函数值向量，由式(15)、式(18)可知：

y′=Q1y, α′=Q1α

(22)

(23)

(24)

则式(21)的离散形式为：

θ1T[(VAQ2+VA′Q1)y-

(25)

θ2T[σ(VIQ2+VI′Q1)α+

(26)

令：

(27)

式(25)、式(26)可写成：

(28)

(29)

(30)

(31)

式中：0为N×N矩阵块。

对于子结构(1)、结构(3)，横截面积A、惯性矩I为常数，上述四式可简化为：

(32)

(33)

(34)

(35)

(36)

式中:I为N阶单位矩阵。

2.3边界条件及系统综合方程

根据式(28)～式(31)、式(32)～式(36)可分别得到3个子结构的未施加约束条件的离散运动方程，现综合各方程得到系统运动方程，令：

qG=[y(1)α(1)y(2)α(2)y(3)α(3)]T

(37)

式中下标(i)代表子结构i，由式(28)、式(32)可得：

(38)

(39)

(40)

(41)

各子结构交界面位移与力的协调条件为：

y(1)(1)=y(2)(N)，y(2)(1)=y(3)(N)

(42)

α(1)(1)=α(2)(N)，α(2)(1)=α(3)(N)

(43)

α′(1)(1)=α′(2)(N)，α′(2)(1)=α′(3)(N)

(44)

y′(1)(1)-α(1)(1)=y′(2)(N)-α(2)(1)

(45)

y′(2)(1)-α(2)(1)=y′(3)(N)-α(3)(1)

(46)

边界条件：y(0,t)=0，α(0,t)=0,α′(L，t)=0,y′(L,t)-α(L，t)=0,离散形式为：

y(1)(N)=0, α(1)(N)=0

(47)

(48)

式 (32)～式 (48) 等12个线性齐次边界条件可表示为：

(49)

其离散形式可表示为：

βq=b

(50)

式中:β为12×6N边界条件矩阵，其每行代表一个边界条件，b为12维零向量，对于式 (42)～式(48) 中的边界条件有：

(51)

式中:e1、eN为N维行向量，其第1个、第N个分量分别为1，其余均为0；对于任意满足式 (50) 的解q可表示为：

(52)

(53)

(54)

(55)

3　算例

3.1固有频率及模态

选取刀具结构参数见表1，材料密度ρ=14.45×103kg/m3，杨氏模量E=580 GPa，剪切模量G=242 GPa，截面剪切系数κ=0.9。得到刀具前四阶固有频率收敛性见图2，当N等于20时，前四阶固有频率分别为：5 089.714 Hz、29 024.152 Hz、71 461.987 Hz、108 043.023 Hz，与文献 [9] 中吻合，结果对比如表2所示。当N继续增大，计算结果相对偏差收敛至<0.000 1%、0.001%、0.002%、0.04%。若只计算一、二阶固有频率，当N=10时，相对偏差便可收敛至<0.05%，映证了Chebyshev谱方法具有的快速收敛性与高精度特性，相较于分段阶梯梁方法具有一定优势。

表1　刀具结构参数

表2　刀具各阶固有频率比较

得到刀具前四阶振型见图3，图3(a)为振动位移y前四阶模态，图3(b)为弯曲角α前四阶模态，各图中竖直线代表刀具各段交界面②、③。从图中可知,刀具变形以刀头部分最大，高阶振型更为显著，三阶、四阶位移模态中，从交界面③处相对位移迅速增大，二阶、三阶、四阶弯曲模态中，从交界面③处相对弯曲角亦迅速增加，说明影响刀具变形量的主要因素是刀头部分参数。

图2　模型收敛性Fig.2　The convergence of the first four natural frequencies of the micro end-mill

图3　刀具前四阶模态振型，N = 20Fig.3　The first four mode shapes and natural frequencies of the micro end-mill when N =20

3.2结构参数影响分析

为合理设计微细立钎刀使之满足高精度的动力学特性要求，需要分析各刀具参数对其固有频率、模态振型的影响，基于所建立的刀具动力学模型，分析了刀柄长度、刀具半锥角、刀头长径比等参数对刀具动力学特性的影响。

图 4为刀柄长度对固有频率的影响，可知其它参数不变时，前四阶固有频率均随刀柄悬长的增加而减小，以一阶固有频率为例，当刀柄长度L1=15 mm时，其值为8 259.901 Hz，而当刀柄长度增加至25 mm时，其值减小至3 440.102 Hz，减幅达58.352%。而在高速微细铣削中，由于刀径减小，为获得较大的切削速度就需要很高的主轴转速，可达150 000 r/min，对于双刃微径铣刀，其切削力频率可达5 000 Hz，因此当刀具一阶固有频率低于切削力频率时极可能造成刀具共振，导致刀具、加工件损坏。因此在满足装卡条件的前提下，应尽可能缩短刀柄悬伸段长度。

图4　刀柄长度对固有频率的影响Fig.4　Change of natural frequencies with length of shank for micro-endmill

图5为刀颈段半锥角对刀具固有频率的影响，可知其它参数不变时，刀具前四阶固有频率均随半锥角的增大而增大，增幅逐渐减小。以一阶固有频率为例，当半锥角从6°到10°时，其值由4 086.832 Hz增大到4 944.045 Hz，增加857.213 Hz，从10°到14°时，增加428.826 Hz至5 372.871 Hz。因此，适当增加刀颈半锥角有利于提高刀具固有频率。

图5　刀具半锥角对固有频率的影响Fig.5　Change of natural frequencies with taper angle for a micro-endmill

图6为刀头长径比对刀具固有频率的影响，可知刀头长径比影响非常小。只有第四阶固有频率随刀头长径比增加而减小，其它各阶频率基本保持不变。这说明在微细铣刀设计时，刀头长径比应更多关注如何增加刀头静、动刚度，不必过于关注其对刀具固有频率的影响。

图6　刀头长径比对固有频率的影响Fig.6　Change of natural frequencies with ratio of length to diameter of tool for a micro-endmill

4　结　论

(1) 对于微细立铣刀动力学特性分析，Chebyshev谱方法具有良好收敛性和较高的计算精度，在选取较小Chebyshev多项式阶数时，仍然获得低阶固有频率、模态振型较高精度的解。相关结果与分段阶梯梁方法及有限元方法吻和，证明了方法的可行性。

(2) 分析刀具前四阶模态振型可知，刀柄、刀颈及刀头中刀头变形量最大，刀具振动位移、弯曲角度在各段交界面处迅速增大，振型阶数越高越显著。

(3) 刀具各结构参数中刀柄长度对固有频率影响最大，前四阶固有频率随刀柄长度增加而迅速减小；随前刀颈半锥角的增大，前四阶固有频率逐渐增大，但增大幅度逐渐减小；刀头长径比对刀具固有频率的影响很小。

[1] 肖才伟. 振动微铣削动力学建模及其分析[D]. 哈尔滨：哈尔滨工业大学, 2008.

[2] 李迎. 微铣削加工技术研究现状及发展趋势[J]. 电子机械工程, 2008, 24(6):26-32.

LI Ying. Recent adavances in micro milling and its future development trend[J]. Electro-Mechanical Engineering, 2008, 24(6): 26-32.

[3] 陈明君, 陈妮, 何宁, 等. 微铣削加工机理研究新进展[J]. 机械工程学报, 2014, 50(5):161-172.

CHEN Mingjun, CHEN Ni, HE Ning, et al. The research progress of micromilling in machining mechanism[J]. Journal of Mechanical Engineering, 2014, 50(5): 161-172.

[4] MIAO J C, CHEN G L, LAI X M, et al. Review of dynamic issues in micro-end-milling[J]. International Journal of Advanced Manufacturing Technology,2007,31(9):897-904.

[5] SHUNMUGAM M S. Machining challenges: macro to micro cutting[J]. Journal of the Institution of Engineers(India): Series C, 2015, 2(22):1-19.

[6] SHI Y, MAHR F, WAGNER U V, et al. Chatter frequencies of micromilling processes: influencing factors and online detection via piezoactuators[J]. International Journal of Machine Tools & Manufacture, 2012, 56(2):10-16.

[7] 万敏, 张卫红. 铣削过程中误差预测与补偿技术研究进展[J]. 航空学报, 2008, 29(5):1340-1349.

WAN Min, ZHANG Weihong. Overviews of technique research progress of form error prediction and error compensation in milling process[J]. Acta Aeronautica et Astronautica Sinica, 2008, 29(5): 1340-1349.

[8] 张俊, 黄保华, 赵万华,等. 面向动态特性快速求解的铣刀等效建模方法[J]. 振动工程学报, 2013, 26(3):351-356.ZHANG Jun, HUANG Baohua, ZHAO Wanhua, et al. Equivalent modeling of endmills for rapid dynamics prediction[J]. Journal of Vibration Engineering, 2013, 26(3): 351-356.

[9] 方泽平, 王西彬, 刘志兵, 等. 基于Timoshenko梁理论的微细铣刀动力学建模[J]. 振动与冲击, 2014, 33(23): 111-115.

FANG Zeping, WANG Xibin, LIU Zhibing, et al. Dynamic modeling of a micro-endmill based on Timoshenko beam theory[J]. Journal of Vibration and Shock, 2014, 33(23): 111-115.

[10] 方泽平. 微细立铣刀的设计基础理论与刃磨技术研究[D]. 北京：北京理工大学, 2014.

[11] RAHNAMA R, SAJJADI M, PARK S S. Chatter suppression in micro end milling with process damping[J]. Journal of Materials Processing Technology,2009,209(17):5766-5776.

[12] YANG Y, WAN M, MA Y C, et al. An improved method for tool point dynamics analysis using a bi-distributed joint interface model[J]. International Journal of Mechanical Sciences, 2015, 105(2016): 239-252.

[13] YANG Y, ZHANG W H, MA Y C, et al. Generalized method for the analysis of bending, torsional and axial receptances oftool-holder-spindle assembly[J]. International Journal of Machine Tools and Manufacture,2015,99(2015): 48-67.

[14] MUSTAPHA K B, ZHONG Z W. A new modeling approach for the dynamics of a micro end mill in high-speed micro-cutting[J]. Journal of Vibration & Control, 2013, 19(6):901-923.

[15] 李雪慧. 截断Chebyshev多项式的谱方法求解数值微分问题[D]. 兰州：兰州大学, 2010.

[16] YAGCI B, FILIZ S, ROMERO L L, et al. A spectral-Tchebychev technique for solving linear and nonlinear beam equations[J]. Journal of Sound & Vibration,2009,321(1):375-404.

[17] TREFETHEN L N. Spectral methods in MATLAB[M]. Philadelphia, Pennsylvania: Society for Industrial & Applied Mathematics , 2001.

[18] 王健平. 谱方法的基本问题与有限谱法[J]. 空气动力学学报, 2001, 19(2):161-171.

WANG Jianping. Fundamental problems in spectral methods and finite spectral method[J]. Acta Aerodynamica Sinca, 2001, 19(2): 161-171.

[19] BOYO J P. Chebyshev and fourier spectral methods[M]. 2nd ed. New York: Dover Publications, 2000.

Dynamic analysis of micro-endmill by Chebyshev spectral method

HUANG Yixin1, YIN Qingfeng2, ZHAO Yang2

(1. School of Astronautics, Harbin Institute of Technology, Harbin 150001, China；2. Institute of Machinery Manufacturing Technology, China Academy of Engineering Physics, Mianyang 621900, China)

A Chebyshev spectral method for studying the dynamic characteristics of micro-endmill was presented. Considering the shear deformation and rotary inertia of micro-endmill, the uniform and tapered Timoshenko beam models were used in the dynamic analysis of the segments of endmill. The discrete forms of the dynamic models were gained by Chebyshev spectral method and synthesized by dynamic substructure technique to get the equation of motion of the whole system. A software package for solving the natural frequencies and modal shapes was developed. To validate the method, the impacts of structural parameters on dynamic characteristics were analysed. The simulation results were compared with those obtained by the stepped beam method and finite element method. It is shown that the calculated result converges into a range of 0.04% when the order of polynomials is larger than 16. The method is of good precision and can be applied to optimize structural parameters of micro-endmill.

micro-endmill; Chebyshev spectral method; dynamic characteristics; dynamic substructure technique

国家“973”计划(2013CB733004)

2015-11-20修改稿收到日期：2016-02-04

黄意新 男，博士生，1987年生

赵阳 男，教授，博士生导师，1968年生

TH122；TG714

A DOI:10.13465/j.cnki.jvs.2016.14.005