柔性空间机器人基于关节柔性补偿控制器与虚拟力概念的模糊全局滑模控制及振动主动抑制

梁　捷， 陈　力 ， 梁　频

(1.福州大学 机械工程及自动化学院，福州　350108；2. 中国空气动力研究与发展中心，四川 绵阳　621000； 3. 电子科技大学 航空航天学院，成都　611731)



柔性空间机器人基于关节柔性补偿控制器与虚拟力概念的模糊全局滑模控制及振动主动抑制

梁捷1,2,3， 陈力1， 梁频2

(1.福州大学 机械工程及自动化学院，福州350108；2. 中国空气动力研究与发展中心，四川 绵阳621000； 3. 电子科技大学 航空航天学院，成都611731)

空间机器人系统的柔性主要体现在空间机器人的臂杆和连接各臂杆之间的铰关节；由于空间机器人系统结构的复杂性，以往研究人员对同时具有柔性关节和柔性臂的系统关注不够；为此讨论了参数不确定情况下柔性关节、柔性臂空间机器人系统的动力学模拟、运动控制方案设计和以及臂、关节双重柔性振动的分阶主动抑制问题。依据线动量、角动量守恒关系并基于拉格朗日方程、线性扭转弹簧及假设模态法推导了系统动力学模型；以此为基础;针对空间机器人实际应用中各关节铰具有较强柔性的情况，引入了关节柔性补偿控制器并结合奇异摄动技术将整个系统分解成独立时间尺度的电机力矩动力子系统和柔性臂子系统；针对电机力矩动力子系统，设计了力矩微分反馈控制器来抑制关节柔性引起的系统弹性振动；针对柔性臂子系统，提出了一种基于虚拟力概念的自适应模糊全局滑模控制方案，由于运用了虚拟力的概念，从而通过仅设计一个控制输入就可达到既跟踪期望轨迹又抑制柔性臂柔性振动的控制目标。计算机数值仿真对比实验证实了该方法的可靠性和有效性。

柔性关节柔性臂空间机器人；关节柔性补偿控制器；虚拟控制力 ；全局滑模控制；双柔性振动分阶主动抑制

在空间机器人动力学分析及控制算法设计中通常将空间机器人系统模化为由刚性杆和刚性关节铰组成的多刚体系统[1-5]，然而，随着航天科技及空间机器人技术的不断发展、成熟，对空间机器人从事任务的要求越来越高精度化、高智能自主化。在这种情况下，原本粗放操作任务中被忽略的柔性效应对空间机器人特性的影响受到各国学者的高度重视[6-9]。但上述研究都忽略了关节柔性，早期的空间机器人柔性研究多集中在杆件柔性上。由于制造技术上的原因，空间机器人驱动关节的柔性不可忽略。如：其中齿轮的弹性、传动轴的扭动以及谐波减速器等装置，都会导致关节柔性的产生并使其容易产生振动。文献[10]研究了弹性关节机器人的建模与控制；文献[11]运用局部状态反馈线性化技术和积分反推控制设计方法，研究了柔性关节机器人全局输出反馈跟踪控制的问题。文献[12]提出一种针对系统参数的不确定性的柔性关节机器人的自适应控制方法。文献[13]讨论了在不确定系统惯性参数下，具有一般柔性关节空间机械臂的动力学建模与非奇异模糊Terminal滑模控制问题。文献[14]对柔性杆柔性关节的机器人进行运动学、动力学分析，并运用Kane法和假设模态法推导出系统动力学方程。文献[15]利用Lagrange方程及假设模态法推导出柔性关节、柔性臂机器人的动力学模型，并将系统分解为表示柔性关节的子系统和表示柔性臂的子系统。但值得注意的是，目前对柔性关节特别是同时考虑了柔性关节和柔性臂系统的研究主要集中于地面固定基机器人，而对于空间机器人的研究还极为少见。空间机器人由于所处太空微重力环境的特殊性，使其具有与地面机器人显著不同的动力学与控制特点。例如，空间机器人系统在很多情况下存在：动量与动量矩两者均守恒的动力学约束形式。且由于动量矩守恒的不可积性，使得系统表现出非完整动力学特性。因此漂浮基柔性关节、柔性臂空间机器人系统的动力学模拟及智能控制系统设计面临着：非完整动力学约束、关节柔性、机械臂柔性三者共存的突出难点，而空间机器人操作期间关节铰的柔性振动与机械臂杆件柔性振动间的相互干扰与动力学耦合效应，使问题变得更加复杂；这将使目前地面固定基机器人的控制方法很难直接推广、应用于空间机器人系统。

基于以上讨论，研究了柔性铰及机械臂杆件柔性同时存在的情况下，本体姿态和位置均不受控的漂浮基空间机器人系统的动力学模拟、运动控制方案设计及双重柔性振动的分阶主动抑制问题。

1　柔性关节、柔性臂空间机器人系统数学模型

柔性关节、柔性臂空间机器人系统结构见图1。图1中:B0为本体，B1为刚性臂，B2为柔性臂。B1与B0、B2与B1的铰接为柔性旋转关节O1和O2。建立惯性坐标系(OXY)及各分体Bj(j=0,1,2)的主轴坐标系(Oj-xjyj)，并设各分体在(OXY)平面内作平面运动。各符号定义为：

本体Bi(i=0,1)的质心OCi相对于惯性坐标系原点O的矢径为ri，r2为B2上坐标x2(0≤x2≤l2)点处的矢径，系统总质心C相对于O的矢径为rc。本体B0的姿态转角为θ0，刚性臂B1及柔性臂B2的运动转角分别为θ1和θ2；关节O1和O2处驱动电机转子的自转角度分别为θa1和θa2。各分体Bj(j=0,1,2)的转动角速度为vj，电机转子的自转角速度为vaj。

图1　柔性关节、柔性臂空间机器人系统Fig.1　Free-floating space robot with flexible links and joints

1.1柔性关节简化模型

根据文献[10]的假设，柔性关节可简化为刚度系数为k的无惯量线性扭簧(见图2)，电机转子与机械臂之间的联接为柔性，当关节Oi(i=1,2)处的电机转子转过角度θai时，受其驱动的机械臂Bi由于扭簧弹性力的作用，其转动角度为：θi=θai-ai，其中ai为柔性关节引起的转动误差。因此，电机转子与机械臂之间弹性力为ki(θai-θi)。

图2　柔性关节的简化模型Fig.2　Simple model of flexible-joint

1.2柔性臂简化模型

(1)

(2)

考虑柔性杆B2为悬臂梁，所以其模态函数为：

(3)

1.3拉格朗日函数法建模

根据系统位置几何关系及系统总质心定义，可将各分体矢径rj(j=0,1,2)表示为：

rj=rc+Rj0e0+Rj1e1+Rj2e2+(Rj3δ1+Rj4δ2)e3

(4)

式中：Rj0,Rj1Rj2,Rj3,Rj4为惯性参数组合函数。

对rj求一阶导，则：

(5)

忽略微弱的重力并假设系统为无外力作用的无根多体系统，系统相对于惯性坐标系(OXY)满足线动量、角动量守恒关系。不失一般性，假设系统的初始线动量、角动量为零，则线动量守恒关系为：

(6)

角动量守恒关系为：

(7)

整理并移项，式(7)可写为:

(8)

Fi(i=1,…,7)与系统参数、广义坐标有关。

分析可知系统总动能T为空间机器人的动能和电机转子动能之和， 表示为:

(9)

忽略重力势能，系统的总势能为柔性臂的弯曲应变能和柔性关节引起的弹性势能之和，即

由拉格朗日第二类方程及上面的系统动能和势能表达式，可以导出载体位置、姿态均不受控的漂浮基柔性关节、柔性臂空间机器人系统完全驱动形式的动力学方程：

(11)

(12)

τ=Ka(θa-θ)

(13)

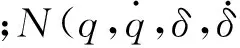
2　智能控制系统设计

针对柔性关节、柔性臂空间机器人实际应用中各关节铰具有较强柔性的实际情况，引入了关节柔性补偿控制器τf并结合奇异摄动技术将整个系统分解成独立时间尺度的电机力矩动力子系统和柔性臂子系统。针对电机力矩动力子系统式(19)，设计了力矩微分反馈控制器来抑制关节柔性引起的系统弹性振动。针对柔性臂子系统式(30)，提出了一种基于虚拟力概念的自适应模糊全局滑模控制方案，实现了对系统柔性臂刚性部分的关节轨迹跟踪和柔性臂振动抑制。因此系统总的控制律为三部分组成:① 柔性关节补偿律τf，② 电机力矩动力子系统控制律τJ，③ 柔性臂子系统控制律τL。将三个控制律加以叠加得到的联合控制律τm=Kn(τJ+τL)+τf，就可同时实现对柔性关节、柔性臂空间机器人系统期望运动轨迹的跟踪和柔性关节、柔性臂双重柔性振动的主动抑制，所设计的控制方案原理见图3。

图3　柔性关节、柔性臂空间机器人控制原理图Fig.3　Schematic diagram of space-based robot system with with flexible links and joints

2.1柔性关节补偿后奇异摄动分解

带有柔性关节的空间机器人最大控制难点是机械臂各关节铰的电机输出转角与其实际转角存在不同步性，这相当于在关节驱动器和被驱动连杆间设置了一个力矩滤波器。关节刚度越小，滤波器的带宽也越窄。为削弱柔性关节带来的影响，引入一种关节柔性补偿器以提高关节等效刚度。

由式(12)和式(13)可得电机力矩动力子系统:

(14)

引入柔性关节补偿器，设计关节驱动电机控制律

τm=Knτn+τf

(15)

τf=-Kfτ

(16)

式中:Kn∈R2×2为常值矩阵;τn为待设计的控制量;τf为关节柔性补偿器;Kf∈R2×2为对角正定系数矩阵。令Kn=I+Kf，I∈R2×2为单位阵，将式(15)和式(16)代入式(14)可得:

(17)

比较式(17)和式(14)可知,通过适当的选取Kf可以提高关节等效刚度。

柔性关节补偿后，再基于奇异摄动法将系统分解成关于电机力矩τ的动力子系统和柔性臂子系统。由奇异摄动理论，控制量τn可设计为:

τn=τJ+τL

(18)

式中：τJ为电机力矩动力子系统的控制律，目的是使该子系统式(17)稳定；τL为柔性臂子系统的控制律，目的是使机械臂关节角θ跟踪给定的期望轨迹θd同时主动抑制柔性杆的振动。

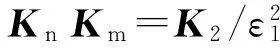
(19)

设计电机力矩动力子系统的微分增益反馈控制律

(20)

以实现如下电机力矩动力子系统的稳定性。

(21)

(22)

即

(23)

(24)

从式(22)可知,该动力学方程与柔性臂动力学方程形式相同，因此将该系统称为柔性臂子系统。

由式(24)可解出柔性振动的加速度:

(25)

将式(25)代入式(23)，可得:

(26)

(27)

由于本身结构的复杂性，柔性关节、柔性臂空间机器人系统的某些惯性参数(如燃料消耗会导致系统质量变化、机械臂的长度、负载的质量等)是难以精确确定或未知的，因此式(27)中Meq、Neq可表示为:

Meq=Mn+ΔMeq

(28)

Neq=Nn+ΔNeq

(29)

式中：Mn、Nn分别为Meq、Neq在标称系统动力学参数下的估计;ΔMeq和ΔNeq为系统参数不精确估计所引起的建模误差。因此，基于以上讨论，建立适用于工程实际应用的柔性臂子系统的数学模型为:

(30)

式中：Δf=ΔMeq+ΔNeq,为模型不确定项。

2.2柔性臂子系统基于虚拟力概念的自适应模糊全局滑模控制方案设计

上述的柔性关节补偿律τf、电机力矩动力子系统控制律τJ主要用于解决柔性关节对控制系统的影响。本节将针对柔性臂子系统设计基于虚拟期望轨迹的自适应模糊全局滑模控制控制。

2.2.1跟踪虚拟期望轨迹的自适应模糊全局滑模控制

运用虚拟控制力的生成能同时反映柔性模态和刚性运动的虚拟期望轨迹，使针对刚性子系统设计的控制器追踪该虚拟期望轨迹，以实现系统载体姿态及关节角的轨迹跟踪同时主动抑制柔性杆的振动。

设θd=[θ1d,θ2d]T为空间机器人关节铰的期望轨迹，跟踪误差e=θd-θ。虚拟期望轨迹定义为θh=[θ1h,θ2h]T，与实际轨迹的误差定义为er=θh-θ，与期望轨迹的误差定义为eh=θd-θh。eh由式(31)二阶指令生成:

(31)

式中：a,b分别为对角正定常值矩阵；F为虚拟控制力，起到稳定柔性振动和保持刚性运动的作用(虚拟控制力F将在“2.2.2”节中进行设计)。

定义全局滑模面

(32)

条件①可使系统初始状态在滑模面上，条件②保证闭环控制系统的稳定，条件③确保滑模面对时间一阶导数的存在。因此函数p(t)定义为:

(33)

式(32)对时间求导可得:

(34)

为有效克服传统滑模控制的不连续控制方法引起的系统高频抖振，设计改进的指数趋近律以消除或减弱抖振，提高系统的控制品质，设计的趋近律如下:

(35)

由滑模控制理论，可设计如下滑模控制律:

KsS)+Nn+Δf

(36)

为了克服柔性关节、柔性臂空间机器人系统中模型不确定项Δf对滑模控制律τL的影响，利用模糊系统[16]设计了一种自适应算法来逼近系统模型不确定项Δf。模糊逻辑系统主要由四部分组成，即：模糊化、规则基、模糊推理机制及反模糊化。采用高斯函数对各输入变量进行模糊化，模糊推理采用乘积法，去模糊化采用加权平均法。由模糊系统的万能逼近理论，定义模糊逻辑系统来逼近柔性关节、柔性臂空间机器人系统的不确定部分

f=W*Tφ(x)+α

(37)

式中：W*∈RN×2为理想权值矩阵;N为模糊规则数；φ(x)∈RN×1为模糊基函数;x为模糊系统输入;α为模糊逻辑系统的函数逼近误差向量。

(38)

因此系统控制律可修正为:

(39)

跟踪实际期望轨迹的系统控制律为:

(40)

该控制律形式上与式(39)一样，只是跟踪的对象不一样，控制律式(40)不需要虚拟控制力的设计可实现关节角轨迹跟踪控制，但不能主动抑制柔性杆振动。

(41)

(42)

可保证闭环系统渐近稳定。

式中:KW，Kα为对称、正定方阵。

证明：选择Lyapunov函数来证明闭环系统的稳定性:

(43)

(44)

因此闭环系统渐近稳定。在所设计的控制律可使系统的关节角渐近跟踪虚拟期望轨迹。

2.2.2虚拟控制力的设计

所设计的虚拟控制力通过式(31)生成eh产生能同时保证柔性振动抑制和机械臂关节铰跟踪鲁棒性的虚拟期望轨迹。将控制方案(39)代入柔性关节、柔性臂空间机器人控制系统数学模型式(30)，得到闭环系统误差方程

(45)

综合式(45)和式(30)，可得柔性关节、柔性臂空间机器人系统的实际跟踪误差方程：

(46)

式中：

(47)

由式(24)可得标称模型柔性振动系统为:

(48)

式中:矩阵带有上标“—”表示中相应的标称模型。

将式(47)代入式(48)可得振动模态方程:

(49)

由式(46)和式(49)得到包含柔性臂振动模态和实际跟踪误差的状态方程:

(50)

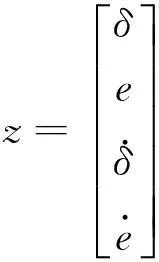
式中:ΦG，ΦV为线性时变矩阵;E为非线性时变矩阵。将矩阵E视为干扰，使用线性二次型最优控制，并以减少状态向量z和控制能量F为优化目标:

(51)

式中：Q∈R8×8和r∈R2×2为正定、半正定常值矩阵;则状态反馈最优控制为:

(52)

式中:G为对称、正定常值矩阵。且是黎卡提方程的唯一解:

(53)

因此，闭环系统式(50)为:

(54)

当E=0该状态反馈最优控制可保证闭环系统稳定。

3　仿真试验结果与分析

以做平面运动的柔性关节、柔性臂空间机器人系统为例(见图1)。Oc0与O1之间的长度为l0;B1和B2的长度分别为l1和l2;Oc1与O1之间的长度为d1。关节O1和O2处电机转子的自转惯量分别为Ia1和Ia2；B0的质量和转动惯量为：m0、I0；B1的质量和转动惯量为：m1、I1；B2的线密度为ρ，抗弯刚度为EI；系统的总质量为：M=m0+m1+ρl2。

仿真时，假设系统真实参数如下：

载体的参数：m0=40 kg，l0=1.5 m，I0=35 kg·m2；刚性杆的参数：m1=4 kg，l1=2 m，a1=1 m，I1=2 kg·m2；柔性杆的参数：l2=2 m，ρ=1 kg/m，EI=200 N·m2；关节电机的转动惯量矩阵：Ia1=Ia2=0.08 kg·m2；柔性关节扭转刚度矩阵Ka=diag(15,15)。

仿真时，设系统的估计模型Mn=0.85Meq，Nn=0.5 Neq。同时，控制系统相关参数选取如下：

Kp=diag(3,3)；ε=diag(0.1,0.1)；Ks=diag(12,12)；λ=10；Kf=diag(6,6)；a=diag[36,36]T；b=diag[12,12]T；r=diag(10,10)；

Q=diag(30,30,30,30,30,30,30,30)

设柔性关节、柔性臂空间机器人的转角期望运动规律为(单位：rad)

系统运动初始构型：θ(0)=θa(0)=[0.05,0.75]T(单位：rad)。仿真时间10 s。

为验证文中设计的关节柔性补偿器式(16)、微分增益反馈控制方法式(20)和基于虚拟力概念的自适应模糊全局滑模控制方案式(39)组成的联合控制律式(15)的有效性，进行了三组仿真对照实验。

第一组:直接采用上述联合控制方案对系统进行数值仿真试验。仿真结果见图4～图7。图4为柔性关节、柔性臂空间机器人机械臂两个关节铰θ1和θ2的轨迹跟踪图，实线表示为期望轨迹，虚线表示为虚拟期望轨迹，点划线表示为实际轨迹；图5为空间机器人机械臂两关节铰电机转子转角θa1和θa2运动的实际轨迹和机械臂两个关节铰θ1和θ2期望运动轨迹的对比图；图6为机械臂关节铰的运动轨迹跟踪误差图；图7为电机转子的转角与机械臂关节铰的期望转角之间的差值eθ的变化曲线图；图8和图9为柔性臂模态坐标变量δ1、δ2的变化曲线图。从仿真结果可知，文中所设计的联合控制方案能够弥补系统惯性参数不确定及柔性关节引起的转动误差，在不是特定的初值情况下，前1/5仿真时段内，实际轨迹即已准确地跟踪虚拟期望轨迹了，体现了设计的联合控制方案具有的良好的实时、在线应用性；同时能够有效抑制柔性关节和柔性臂引起的系统柔性振动，保证系统控制精度和稳定性。

第二组:为关闭联合控制律式(15)中的关节柔性补偿器τf进行的仿真试验。仿真结果见图10～图12所示。图10为关闭关节柔性补偿器τf后机械臂两个关节铰θ1和θ2的轨迹跟踪图；图11和图12分别为机械臂两关节铰电机转子转角θa1和θa2运动的实际轨迹与机械臂两个关节铰θ1、θ2期望运动轨迹的对比图。从仿真结果可知，倘若在仿真过程中未对系统施加关节柔性补偿控制，则系统无法精确完成关节空间的轨迹跟踪任务(见图10)，且电机转子的转角无法跟踪上空间机器人转角的期望运动轨迹(见图11和图12)，这意味着该控制方案不能补偿柔性关节引起的系统角度误差。

图4 空间机器人转角运动轨迹Fig.4Themotiontrajectoriesofspacerobot图5 电机转子转角运动轨迹Fig.5Thetrajectoryofmotorrobots图6 机械臂关节铰的运动轨迹跟踪误差eFig.6Thetrajectorytrackingerrorse

图7 电机转子的转角与机械臂关节铰的期望转角之间的差值eθFig.7Thedifferenceeθ图8 模态坐标变量δ1的变化曲线图(基于虚拟力概念的控制方案)Fig.8Curveofthemodalcoordinatevariableδ1(basedonvirtualcontrolforceconception)图9 模态坐标变量δ2的变化曲线图(基于虚拟力概念的控制方案)Fig.9Curveofthemodalcoordinatevariableδ2(basedonvirtualcontrolforceconception)

图10 空间机器人转角轨迹(关闭柔性补偿器τf)Fig.10Themotiontrajectoriesofspacerobotwhenτfisclosed图11 电机转子转角1运动轨迹(关闭柔性补偿器τf)Fig.11Thetrajectoryofmotorrobotswhenτfisclosed图12 电机转子转角2运动轨迹(关闭柔性补偿器τf)Fig.12Thetrajectoryofmotorrobotswhenτfisclosed

第三组：为利用本文设计的关节柔性补偿器式(16)、微分增益反馈控制方法式(20)和跟踪实际期望轨迹的系统控制律式(40)组成的联合控制律式(15)对系统进行控制时，柔性臂模态坐标变量δ1、δ2的变化曲线图(见图13和图14)。从图8、图9与图13、图14对比可知,基于虚拟力的控制方案能够有效地抑制空间机器人柔性臂的振动，在5 s后，基本消除了柔性臂的振动。

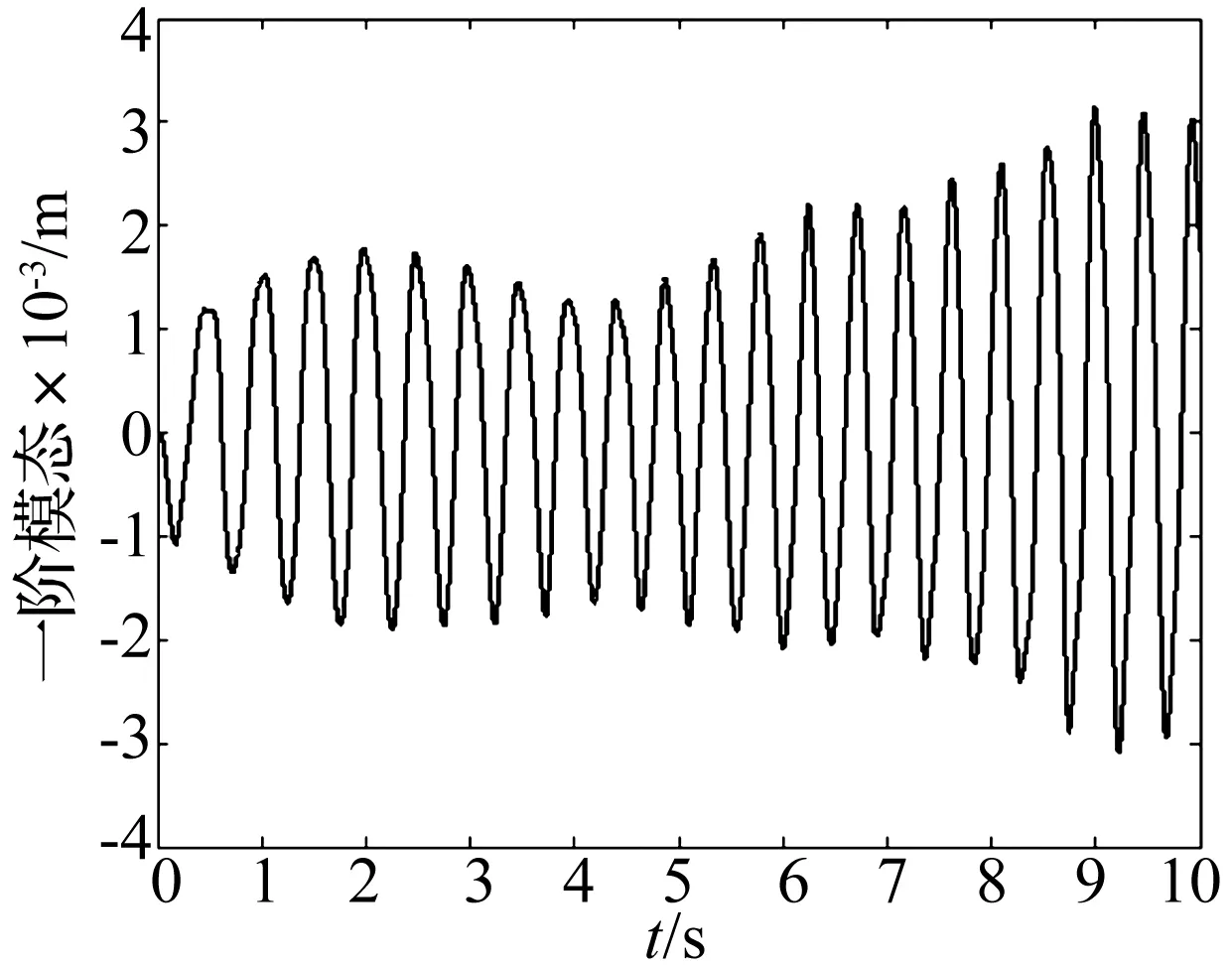
图13　模态坐标变量δ1的变化曲线图(自适应模糊全局滑模控制)Fig.13　Curve of the modal coordinate variable δ1(adaptive fuzzy global sliding mode control scheme)

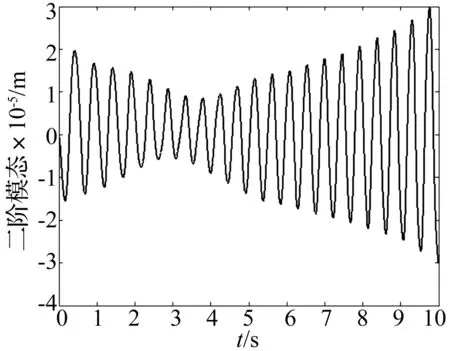
图14　模态坐标变量δ2的变化曲线图(自适应模糊全局滑模控制)Fig.14　Curve of the modal coordinate variable δ2(adaptive fuzzy global sliding mode control scheme)

4　结　论

讨论了综合考虑关节和臂杆柔性的空间机器人动力学模拟、运动控制算法设计和以及臂、关节双重柔性振动的分阶主动抑制问题，主要结论如下：

(1) 文中对柔性关节、柔性臂空间机器人系统进行了动力学模拟。由于在系统动力学模型的推导过程中结合系统动量守恒关系消去了本体位置项，这使得文中设计的联合控制方案具有不需要测量反馈载体位置、速度和加速度的显著优点。

(2) 利用关节柔性补偿器，解除了传统奇异摄动法受关节柔性的约束，导出了空间机器人经关节柔性补偿后的电机力矩动力子系统和柔性臂子系统。

(3) 针对柔性臂子系统，文中设计的基于虚拟力概念的控制方案，使用指令产生器构造了可同时反映关节角及柔性振动模态的虚拟期望轨迹，因此，仅通过设计一个控制输入跟踪虚拟期望轨迹便可同时保证刚性轨迹跟踪并对柔性振动进行主动抑制，与传统基于奇异摄动法将刚性运动控制量与柔性抑制振动控制量进行叠加的组合控制方案[10,13]相比，具有控制器结构简单，调节方便，计算量小，有利于在线实施等特点，从而更适合于在空间机器人控制系统的实际应用。

(4) 通过三组仿真对照试验可知，文中所设计的联合控制方案能够弥补系统惯性参数不确定及柔性关节引起的转动误差，保证柔性关节、柔性臂空间机器人完成期望运动轨迹的渐近跟踪；并能够有效抑制柔性关节和柔性臂引起的系统柔性振动，保证系统控制精度和稳定性。

[1] PISCULLI A, FELICETTI L, GASBARR P, et al. A reaction-null/Jacobian transpose control strategy with gravity gradient compensation for on-orbit space manipulators[J]. Aerospace Science and Technology, 2014, 38: 30-40.

[2] MICHAEL W W. Adaptive control of space-based robot manipulators[J]. IEEE Transactions on Robotics and Automation, 1992, 7(6):828-835.

[3] ABIKO S, HIRZINGER G. An adaptive control for free-floating space robot by using inverted chain approach [C]// Proceedings of the 2007 IEEE/RSJ International Conference on Intelligent Robots and Systems.San Diego, CA: IEEE, 2007: 2236-2241.

[4] 戈新生，陈立群，吕杰. 空间机械臂非完整运动规划的遗传算法研究[J]. 宇航学报, 2005, 26(3): 262-266.

GE Xinsheng, CHEN Liqun, LÜ Jie. Nonholonomic motion planning of a space manipulator system using genetic algorithm[J]. Journal of Asronautics, 2005, 26(3):262-266.

[5] 梁捷，陈力. 时间延迟下双臂空间机器人工作空间轨迹跟踪的改进控制方法[J]. 工程力学,2012,29(10):366-371.

LIANG Jie, CHEN Li. Improved control for dual-arm space robot with time delay to track desired trajectory in inertia space [J]. Engineering Mechanics,2012,29(10):366-371.

[6] KUMAR A, PATHAK P M, SUKAVANAM N. Reduced model based control of two link flexible space robot[J]. Intelligent Control and Automation, 2011, 2:112-120.

[7] 王从庆, 柯昌俊. 自由浮动柔性空间双臂机器人的混合抑振控制[J]. 振动工程学报, 2009, 22(1): 31-35.

WANG Congqing, KE Changjun. Hybrid vibration suppression for a free-floating flexible dual-arm space robot [J]. Journal of Vibration Engineering, 2009,22(1):31-35.

[8] 杜欣，蔡国平. 带有末端集中质量的双连杆柔性机械臂主动控制[J].应用力学学报, 2009, 26(4): 672-678.

DU Xin, CAI Guoping. Active control for two-link flexible manipulator with tip mass[J]. Chinese Journal of Applied Mechanics, 2009, 26(4): 672-678.

[9] 梁捷，陈力. 柔性空间机械臂末端运动及柔性振动的模糊自适应补偿控制[J]. 兵工学报, 2011 , 32(1): 45-57.

LIANG Jie，CHEN Li. Fuzzy logic adaptive compensation control of end-effect montion and flexible vibration for space-based flexible manipulator[J]. Acta Armamentarii，2011,32(1): 45-57.

[10] SPONG M W. Modeling and control of elastic joint robots[J]. Journal of Dynamics Systems，Measurement, and Control, 1987，109(4): 310 -319.

[11] KHODER M, WILSON W. Global output tracking control of flexible joint robots via factorization of the manipulator mass matrix[J]. IEEE Transactions on Robotics, 2009, 25(2): 428-437.

[12] PIOTR S, KRZYSZTOF K. A new control algorithm for robot with joint flexibility[C]//16th IEEE International Conference on Control Applications, Part of IEEE Multi-Conference on Systems and Control. Singapore, 2007: 238-243.

[13] 梁捷, 陈力. 关节柔性的漂浮基空间机器人基于奇异摄动法的轨迹跟踪非奇异模糊Terminal滑模控制及柔性振动抑制[J]. 振动与冲击, 2013, 32(23): 6-12.

LIANG Jie, CHEN Li. Nonsingular fuzzy Terminal sliding mode control based on singular suppression and elastic vibration suppressing of free-floating space robot with flexible joints[J]. Journal of Vibration and Shock,2013,32(23):6-12.

[14] 章定国，周胜丰. 柔性杆柔性铰机器人动力学分析[J]. 应用数学和力学, 2006, 27(5): 615-623.

ZHANG Dingguo, ZHOU Shengfeng. Dynamic analysis of flexible-link and flexible-joint robots[J]. Applied Mathematics and Mechanics, 2006, 27(5): 615-623.

[15] VAKIL M, FOTOUHI R, NIKIFORUK P N. A new method for dynamic modeling of flexible-link flexible-joint manipulators[J].Journal of Vibration and Acoustics, 2012,134(1):14503-14513.

[16] WANG L X, MENDEL J M. Fuzzy basis functions, universal approximation, and orthogonal least square learning [J]. IEEE Transaction on Neural Networks,1992,3(5):807-814.

[17] PATEL R V, TODA M, SRIDHAR B. Robustness of linear quadratic state feedback designs in the presence of system uncertainty [J]. IEEE Trans Automat Control, 1978, 21: 945-949.

Adaptive fuzzy global sliding mode control and active hierarchical vibration suppression of space robot with flexible-link and flexible-joint

LIANG Jie1,2,3, CHEN Li1, LIANG Pin2

(1. Department of Mechanical Engineering and Automation, Fuzhou University, Fuzhou 350108, China；2. China Aerodynamics Research and Development Center, Mianyang 621000 , China；3. School of Astronautics&Aeronautic , University of Electronic Science and Technology of China, Chendu 611731 , China)

The flexibility of space robot system mainly embodies in its arm bars and hinge joints connecting the arm bars. The dynamics simulation of an space robot system with flexible joints and flexible arms were carried out, the motion control algorithm was designed and the active hierarchical vibration inhibition of flexible arms and joints was investigated under the situation of all the parameters uncertain. According to the principle of conservation of momentum and moment of momentum, and based on Lagrange equations, the dynamic model of the system was deduced under the supposition of linear torsion spring and by using the hypothesis modal method. On this basis, considering the actual situation that each hinge joint has strong flexibility in space robot, a flexible joint compensation controller was introduced and making use of the singular perturbation technology, the whole system was decomposed into a motor moment power subsystem and a flexible arm subsystem with independent time scale. For the motor moment power subsystem, a moment differential feedback controller was designed to inhibit the elastic vibration caused by joint flexibility. For the flexible arm subsystem, an adaptive fuzzy global sliding mode control scheme was proposed based on the concept of virtual force. By using the concept of virtual force, the control target of not only tracking the expected trajectory, but also inhibiting the vibration of flexible arm was achieved by only designing a control input. The results of numerical simulations testify the reliability and availability of the scheme proposed.

space robot with flexible-link and flexible-joint; joint flexible compensation controller; virtual force; global sliding mode control; double flexible vibration active hierarchical suppression

国家自然科学基金(11372073;11072061);四川省科技厅应

用基础项目(2016JY0210)

2014-12-11修改稿收到日期：2015-09-17

梁捷 男，博士后，1971年生

TP241

A DOI:10.13465/j.cnki.jvs.2016.14.011