机翼颤振的时滞反馈控制研究

罗梦翔， 高明周， 蔡国平

(上海交通大学 船舶海洋与建筑工程学院，上海　200240)



机翼颤振的时滞反馈控制研究

罗梦翔， 高明周， 蔡国平

(上海交通大学 船舶海洋与建筑工程学院，上海200240)

采用瞬时最优方法对二元机翼颤振的时滞反馈控制进行研究。首先采用Lagrange方法建立机翼系统的颤振动力学模型，其中考虑了机翼俯仰刚度的立方非线性，然后采用瞬时最优控制方法进行了非线性时滞反馈控制律的设计，最后通过数值仿真对控制方法的有效性进行了验证。仿真结果显示，时滞控制律能够有效地抑制机翼的颤振。

机翼；颤振；瞬时最优控制；时滞

飞行器颤振是在其本身运动引起的气动力的激励下发生的一种自激振动。当飞行器的飞行速度超过临界颤振速度时，机翼会不断地从气流中吸取能量，导致振动无法衰减下来，从而给飞行器带来灾难性的破坏。目前机翼颤振问题已经得到越来越多学者的大量关注，并有许多研究成果问世。例如，于明礼等[1-2]考虑机翼外部扰动和建模误差的不确定性，分别设计了H∞鲁棒控制律和μ控制器，并进行了风洞实验验证；WANG等[3]针对含未建模非线性以及外接扰动的二元非线性气动弹性系统，采用高增益状态观测器设计多输入多输出(Multiple-Input Multiple-Output,MIMO)自适应输出反馈控制器，进而抑制结构气动弹性响应和极限环震荡；钱文敏等[4]针对气动弹性系统中由于来流速度扰动引起的不确定性，发展了一种新的不确定性建模方法，该方法从气动弹性建模的根源出发，运用信号变换法则使系统的不确定维数得以降低，进而设计出更为有效的颤振鲁棒控制系统。

然而在主动控制系统中不可避免地存在着时滞现象，控制回路中包含有作动器、传感器和控制器等电子元器件，这些电子元件的动态特性会导致最终作用于结构的控制力产生时滞。已有研究结果显示，即使是小时滞量，也会导致在系统不需要能量时作动器向系统输入能量，从而有可能引起控制效率的下降或控制系统失稳。对于机翼颤振主动控制，目前已有一些学者开始关注控制系统中的时滞问题，例如，ZHAO[5]研究了在不可压流场中时滞对主动控制机翼颤振稳定性的影响，发现在控制回路中，时滞对整个伺服气弹系统有着重要的影响，同时证明了时滞对系统稳定的影响主要与系统的参数和反馈信号的类型有关；LIBRESCU等[6]运用Pontryagin方法结合Stepan定理研究了非线性时滞对气弹系统的影响，发现通过适当的设计，时滞控制比传统的控制方法能够更有效的抑制颤振；YUAN等[7]针对二维高超音速升力面设计了Pyragas型的时滞反馈控制器，分析了受控系统的非线性气动弹性行为；HUANG等[8]通过离散化状态方程，将含输入时滞的状态方程转化为无时滞的状态方程，并在此基础上运用LQG(Linear Quadratic Gaussian)控制方法和卡尔曼观测器进行计入时滞的机翼颤振控制。在此值得说明的是，对于机翼颤振问题，目前绝大多数的研究工作是集中在主动抑制方法上，而关于其中时滞问题的研究非常少。飞行器的飞行速度一般很高，在非常短的时间间隔里系统的状态也会出现很大不同，因此非常小的时滞量也会对控制性能造成大的影响。可以说，关于机翼颤振主动控制中的时滞问题还有许多问题有待研究。

本文对机翼颤振的时滞反馈控制方法进行研究，其中考虑了机翼刚度的立方非线性，控制律的设计采用瞬时最优控制方法进行设计，最后通过数值仿真对所给方法的有效性进行了验证。

1　颤振模型建立

二元机翼的模型见图1，机翼展长为s，弦长为c。机翼根部有两个转动弹簧分别提供沉浮h(向下为正)和俯仰θ(机翼前缘抬头为正)两个自由度运动，它们的弹簧刚度分别为Kh和Kθ，这两个自由度之间无刚度耦合。Q和P分别为气动中心和弹性轴，xf为机翼前缘到弹性轴的距离，气动中心和弹性轴的距离为ec，e为偏心率。操纵面还有一个偏转自由度β(向下为正)，当操纵面的铰接刚度足够大时，可以忽略操纵面惯性的影响，二元机翼退化成两个自由度，操纵面仅作为一个激励装置，与机翼基本气动升力无关，且可以偏转到任意期望的角度[9]。

图1　带操作面的二元机翼模型Fig.1　Two-dimensional airfoil model with control surface

机翼上任意一点在垂直方向的位移(向下为正)为：

z=h+(x-xf)θ

(1)

系统动能、势能以及耗散能分别为：

(2)

(3)

(4)

式中：m为机翼单位面积质量，Ch和Cθ分别为沉浮和俯仰两个自由度弹簧的阻尼。

采用片条理论得到机翼每个片条元上简化的气动升力和绕弹性轴气动力矩分别为[9-10]：

(5)

(6)

作用在翼面的气动力和气动力矩做的虚功为：

δW=∫[-dLδh+dMfaδθ]

(7)

因此，广义力可表示为：

(8)

(9)

将系统动能、势能、耗散能及广义力代入拉格朗日方程，可得二元机翼气弹运动方程为：

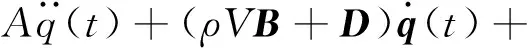
(ρV2C+E)q(t)=0

(10)

式中：q(t)=[h(t),θ(t)]T为浮沉和俯仰自由度的广义坐标向量；A、B、C、D和E分别为机翼系统的惯性、气动阻尼、气动刚度、结构阻尼和结构刚度矩阵，表达如下：

操纵面偏转角β改变会产生气动升力Lc和气动力矩Mc，操纵面的控制力为：

(11)

弹性机翼的大变形会导致结构立方非线性，也就是说此时刚度非线性与立方硬弹簧特性具有类似的动力学特性。考虑俯仰刚度的立方非线性特征，即：

M(θ)=Kθθ+enlKθθ3

(12)

式中：enl为非线性刚度系数。将系统的动能、势能、耗散能、考虑了俯仰刚度立方非线性以及操纵面的控制力代入拉格朗日方程中，可以得到：

f(t)=bβ

(13)

式(13)可化为：

(14)

式中：

2　瞬时最优时滞反馈控制

式(14)是一个标准的非线性状态方程，这里我们采用由YANG等[11]提出的瞬时最优控制方法设计非线性控制律。对于时滞反馈控制律的设计方法，文献[12]中有详细地介绍。

在式(14)中考虑控制项的时滞，则系统的时滞状态方程为：

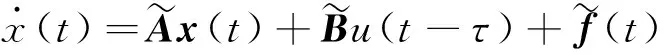
(15)

式中：τ为时滞量。以下针对状态方程式(15)设计时滞反馈控制律。

对式(15)进行如下的积分变化[13]：

(16)

从而可以将式(15)转化为如下不显含时滞的非线性状态方程形式：

(17)

瞬时最优控制是一种基于四阶Runge-Kutta算法的控制设计方法，它可以处理非线性系统的控制设计。对式(17)采用四阶Runge-Kutta法，其解可以写成如下形式：

(18)

(19)

式中：A0、A1、A2及A3表达如下：

(20)

取如下性能指标：

J(t)=HT(t)QH(t)+uT(t)Ru(t)

(21)

式中：Q为非负定对称矩阵，R>0为任意正数。瞬时最优控制设计是在式(18)的约束下设计控制律，使得每一步的性能指标J取极小值。为此，定义如下Hamilton函数：

YH=HT(t)QH(t)+uT(t)Ru(t)+

(22)

式中：λ为Lagrange乘子列阵。通过：

(23)

可以得到瞬时最优控制律为：

(24)

由式(24)可知，控制律u(t)是H(t)的函数，而由式(16)可知,H(t)包含有积分项，该积分项的详细迭代计算格式可参考文献[13]。

3　数值仿真

本文在此进行数值仿真，验证所给方法的有效性。二元机翼结构参数见表1。首先采用V-g法[14]确定机翼的临界颤振速度。图2为风速V和人工阻尼g之间的关系。V-g法中人工阻尼g的物理意义为：假如机翼的真实结构阻尼正好等于这个g值，则在所设定的风速V和空气密度ρ的状态下机翼做简谐振动。由图2可知，当速度达到V=509.08 m/s时，俯仰角对应的g值穿过零点，由负值变为正值，故此颤振临界速度为V=509.08 m/s，机翼速度大于该值将发生颤振。

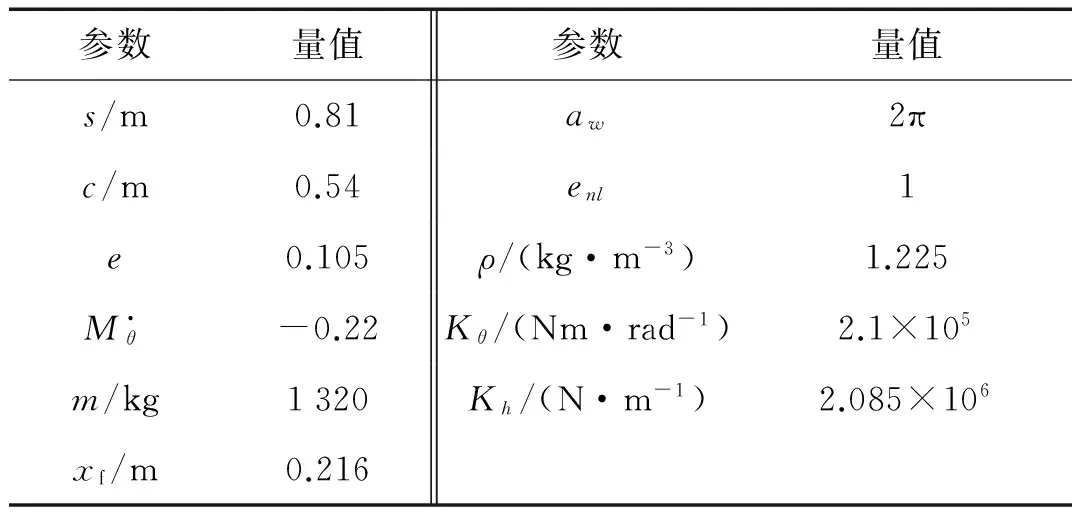
表1　二元机翼结构参数

数值仿真中取风速为600 m/s，该值大于临界颤振速度。假定机翼有一个初始的沉浮位移h=0.5 m和初始俯仰角度θ=0.05°。为了显示本文所给时滞处理方法的有效性，本文在此考虑大时滞量问题，控制系统中的时滞量取值为τ=0.1 s。控制设计时，取式(21)中控制增益为Q=I4×4和R=10。由于控制信号是操纵面的偏转角度，本文中要求最大偏转角为±5°。图3为施加时滞反馈控制后机翼的沉浮位移、 俯仰角和操纵面偏转角时程，不施加控制的结果也在图中予以显示。从图3可知，当对机翼不施加任何控制措施时，沉浮位移在气动阻尼的影响下会逐渐衰减；由于系统中存在立方非线性，当风速超过临界颤振速度时，俯仰角响应在原点附近出现稳定的周期解，产生极限环颤振，这种情况容易使机翼产生疲劳断裂。施加时滞反馈控制后，机翼的响应能够在很短的时间内得到抑制。在此需要说明：当时滞量取小于0.1 s的任意值时，本文中的时滞处理方法都能够有效地抑制机翼系统的颤振。

图2　风速与人工阻尼关系Fig.2　Relation of wind speed and artificial damping

图3　控制仿真结果Fig. 3 Control simulation results

4　结　论

本文对二元机翼颤振的时滞反馈控制进行了研究，给出了机翼颤振系统的动力学模型，采用瞬时最优控制方法进行了时滞反馈控制律的设计，数值仿真中采用V-g法获得了机翼的临界颤振速度。仿真结果显示出，本文所给出的时滞问题处理方法能够有效地处理控制系统中的时滞，时滞反馈控制律能够有效地抑制机翼的颤振。

[1] 于明礼, 文浩, 胡海岩. 二维翼段颤振的H∞控制[J]. 振动工程学报, 2006, 19(3): 326-330.

YU Mingli, WEN Hao, HU Haiyan. Active flutter suppression of a two-dimentional airfoil using H∞synthesis [J]. Journal of Vibration Engineering, 2006, 19(3): 326-330.

[2] 于明礼, 文浩, 胡海岩, 等. 二维翼段颤振的μ控制[J]. 航空学报, 2007, 28(2): 340-343.

YU Mingli, WEN Hao, HU Haiyan, et al. Active flutter suppression of a two dimensional airfoil section usingμsynthesis [J]. Acta Aeronautica et Astronautica Sinica, 2007, 28(2): 340-343.

[3] WANG Z, BEHAL A, MARZOCCA P. Model-free control design for multi-input multi-output aerolastic system subject to external disturbance [J]. Journal of Guidance, Control, and Dynamics, 2011, 34(2): 446-458.

[4] 钱文敏, 赵永辉, 胡海岩. 二元机翼/外挂系统的颤振鲁棒抑制[J]. 中国科学: 物理学, 力学, 天文学,2013,43(4):334-344.

QIAN Wenmin, ZHAO Yonghui, HU Haiyan. Robust flutter suppression for a 2-dimensional wing-store system [J]. Scientia Sinica Physica, Mechanica & Astronomica, 2013, 43(4): 334-344.

[5] ZHAO Y H. Stability of a time-delayed aeroelastic system with a control surface [J]. Aerospace Science and Technology, 2011, 15(1): 72-77.

[6] LIBRESCU L, MARZOCCA P. Aeroelasticity of 2D lifting surfaces with time-delayed feedback control [J]. Journal of Fluids and Structures, 2005, 20: 197-215.

[7] YUAN Y, YU P, LIBRESCU L, et al. Aeroelasticity of time-delayed feedback control of two-dimensional supersonic lifting surfaces [J]. Journal of Guidance, Control, and Dynamics, 2004, 27(5): 795-803.

[8] HUANG R, HU H, ZHAO Y. Designing active flutter suppression for high-dimensional aeroelastic systems involving a control delay [J]. Journal of Fluids and Structures, 2012, 34: 33-50.

[9] 王囡囡. 二元机翼颤振及其主动控制的研究[D]. 徐州：中国矿业大学, 2013.

[10] BISPLINGHOFF R L, ASHLEY H. Principles of aeroelasticity [M]. New York: Courier Dover Publications, 1962.

[11] YANG J N, LI Z, DANIELIANS A, et al. Aseismic hybrid control of nonlinear and hysteretic structures II [J]. Journal of Engineering Mechanics, 1992, 118(7): 1441-1456.

[12] 蔡国平, 陈龙祥. 时滞反馈控制的若干进展[J]. 力学进展, 2013, 43(1): 21-27.

CAI Guoping, CHEN Longxiang. Some problem of delayed feedback control [J]. Advances in Mechanics, 2013,43(1):21-27.

[13] CAI G P, HUANG J Z. Instantaneous optimal method for vibration control of linear sampled-data systems with time delay in control [J]. Journal of Sound and Vibration, 2003, 262(5): 1057-1071.

[14] 赵永辉. 气动弹性力学与控制[M]. 北京：科学出版社, 2007.

Delayed feedback control for airfoil flutter

LUO Mengxiang, GAO Mingzhou, CAI Guoping

(School of Naval Architecture and Ocean Civil Engineering, Shanghai Jiao Tong University, Shanghai 200240, China)

The delayed feedback control for a two-dimensional airfoil flutter was investigated. The dynamic equation for airfoil flutter was established using the Lagrange equation, in which the cubic nonlinearity describing the wing pitching stiffness was taken in account. Then the instantaneous optimal control method was used to design a nonlinear delayed feedback controller. Finally, numerical simulations were carried out to demonstrate the effectiveness of the proposed controller. The simulation results indicate that the delayed feedback controller proposed can effectively suppress the airfoil flutter.

airfoil; flutter; instantaneous optimal control; time delay

国家自然科学基金(11132001;11272202;11472171);上海市教委科研重点项目(14ZZ021);上海市自然科学基金(14ZR1421000)

2015-04-17修改稿收到日期：2015-08-31

罗梦翔 女，硕士生，1992年生

蔡国平 男，博士，教授，1956年生

V214.3

A DOI:10.13465/j.cnki.jvs.2016.14.010