卫星链路CSSDS标准删除卷积码的识别方法
胡以华,许建华,王 磊,向长波
(1.电子工程学院脉冲功率激光技术国家重点实验室,安徽 合肥 230037;2.电子制约技术安徽省重点实验室,安徽 合肥 230037;3.中国电子科技集团公司第41研究所,山东 青岛 266555)
卫星链路CSSDS标准删除卷积码的识别方法
胡以华1,2,许建华3,王磊1,2,向长波3
(1.电子工程学院脉冲功率激光技术国家重点实验室,安徽 合肥 230037;2.电子制约技术安徽省重点实验室,安徽 合肥 230037;3.中国电子科技集团公司第41研究所,山东 青岛 266555)
介绍了删除卷积码的定义,根据删除卷积码与源卷积码之间的关系,构建了删除卷积码识别的数学模型。考虑误码情况,针对Walsh-Hadamard变换在删除卷积码校验矩阵的识别中存在运算量和数据量过大的问题,对校验矩阵方程组进行了变形,提出了改进Walsh-Hadamard算法,能够有效地识别出校验矩阵。在此基础上识别源码的生成矩阵和删除模式,并通过真实卫星链路构建实验平台进行删除卷积码识别实验。
删除卷积码;校验矩阵;生成矩阵;识别;实验平台
0 引言
卫星链路中的卷积码广泛采用了CCSDS的编码标准,如美国的天基红外系统SBDRS、法国的卫星星座ESSAIM和英国的战术光学卫星。目前的卷积码盲识别方法主要是针对1/2码率的卷积码,如高斯直接求解法、快速双合冲算法和欧几里德算法等[1-3];文献[4]首次将Walsh-Hadamard变换用于卷积码识别,但也是针对1/2码率的卷积码;文献[5]在识别出删除卷积码校验矩阵的基础上求解源卷积码编码参数,没有考虑误码对校验矩阵识别的影响;文献[6]采用试凑法和错误位置穷举法识别删除卷积码,要求误比特率小于0.005。以上方法均缺少实际卫星链路的验证和对真实卫星通信信号的编码识别。本文研究了较低信噪比和较高误比特率情况下的卫星链路删除卷积码识别方法,并构建了卫星链路编码实验平台进行编码识别实验,该平台也可用于对实际卫星通信信号进行编码识别。
1 删除卷积码的特性
卷积码是将发送的信息元通过一个线性的、有限状态的移位寄存器而产生的码,与分组码不同,卷积码的校验元不仅与当前时刻的信息元有关,还与此前各时刻输入至编码器的信息元有关。设G(D)为生成多项式矩阵,把信息序列和相应的码序列也写成多项式的形式即M(D)和C(D),则[7]:

(1)
通过删除(2,1,m)源卷积码C特定位置的码元即可得到删除卷积码, 将信息元k位分为一组,k为分组长度,分组后输入(2,1,m)卷积码编码器,并把其输出的码字看成是(2k,k,m)卷积码C′的码字,设G(D)是C的生成多项式矩阵,G′(D)是C′的生成多项式矩阵,P是删除模式,将G′(D)与P中“0”值所对应的列向量删除,得到Cp的生成多项式矩阵Gp(D),删除卷积码也可以用其生成多项式矩阵Gp(D)描述。
2 改进Walsh-Hadamard变换的删除卷积码识别方法
2.1数学模型
删除卷积码的识别可以分为两步:1)根据接收的含错码序列Rp(D),识别Cp的最简校验多项式矩阵;2)根据最简校验多项式矩阵,计算源卷积码的生成多项式矩阵和删除模式P。
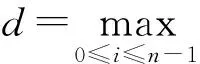


(3)
对于含有误码的码元序列,则R(D)=C(D)+E(D),其中E(D)为误码多项式,R(D)为接收到的数据多项式,由于误码导致实际的校验多项式矩阵不能满足式(3)的每一个方程,则卷积码的识别问题转化为计算满足式(3)中方程个数最多的一组解向量。
通过式(3)求解删除卷积码的最简校验多项式矩阵,必须构造恰当的系数矩阵,即选取正确的参数d和n。假设删除卷积码的实际码率为(n′-1)/n′,最简校验多项式矩阵最大次数为d′,由方程组可知:
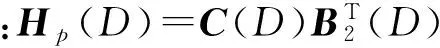
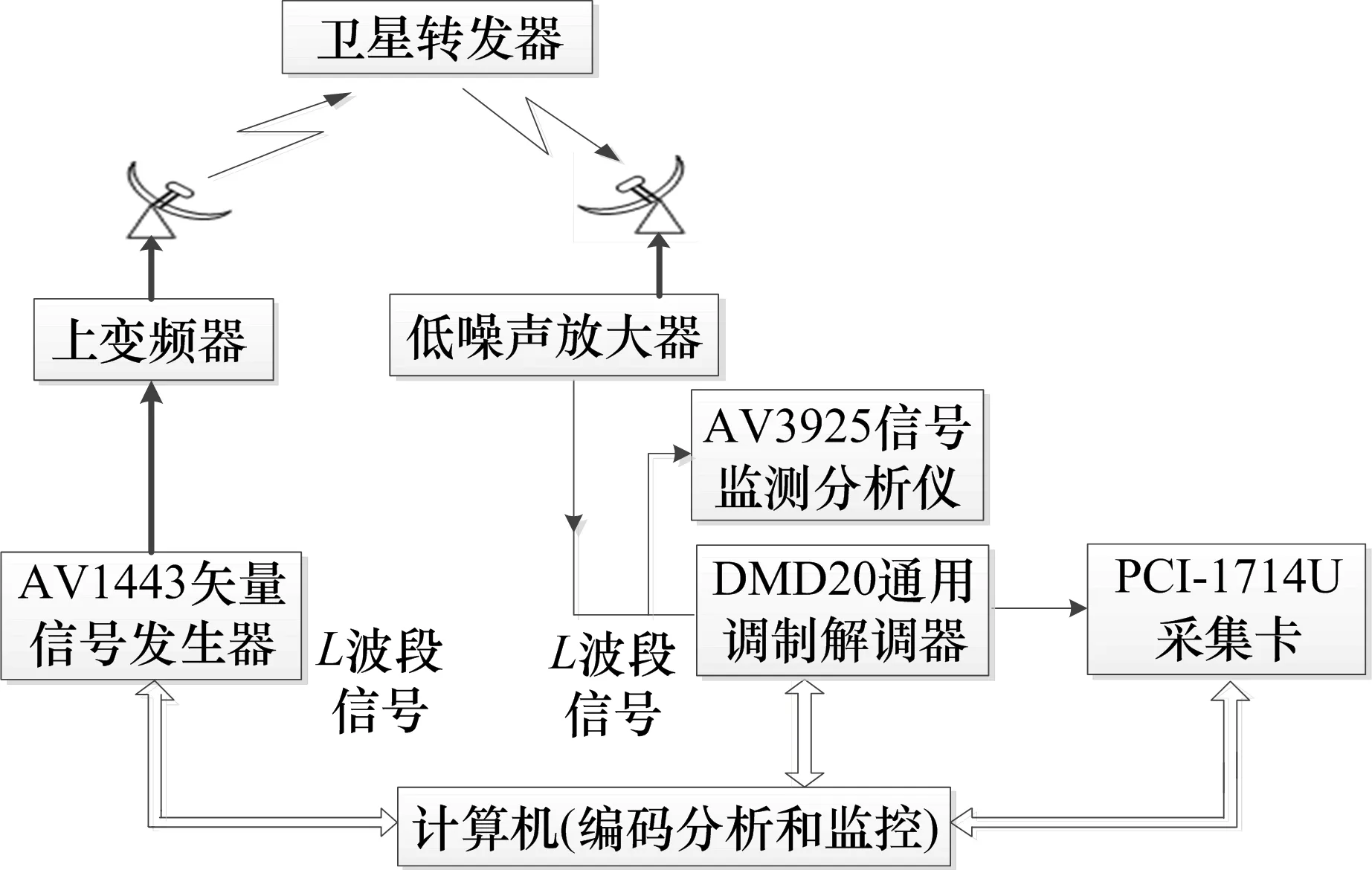
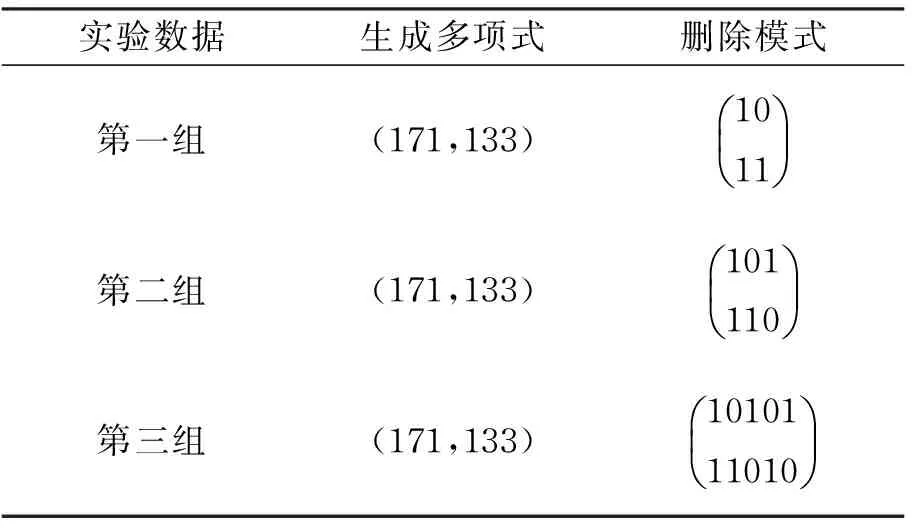
2)当d≥d′,n 因此,在构造系数矩阵时,应当选取较大的d值,对于CCSDS标准的卷积码,取d=6[7],从小到大遍历所有n值(实际中n≤8)。当取到n=n′时,即可求解方程组,将其中任一解化简即可得到最简校验多项式矩阵。 定理1[6]:设H(D)=(h0(D),h1(D),…,hn-1(D))是一个码率为(n-1)/n的卷积码的校验矩阵,则存在码率为1/2的卷积码和删除模式P,使得由它生成的删除卷积码的校验矩阵为H(D),生成矩阵G(D)=(g1(D),g2(D))可按如下方式确定: (4) (5) 删除模式为: (6) 可知,任何(n-1)/n删除卷积码均能够由码率为1/2的源卷积码通过删除生成,并且生成矩阵和删除模式可以通过删除卷积码的校验矩阵求得。 2.2校验矩阵估计 文献[4]采用Walsh-Hadamard变换的方法计算式(3)符合率最高的解,Walsh-Hadamard采用蝶形运算实现[8],算法的时间复杂度由蝶形运算决定,对于高码率的删除卷积码,(d+1)×n较大,运算量较大,并且需要的内存空间太大,超出了计算机内存的承受范围,因此对算法作如下改进: 首先,对式(3)的方程组进行变形,生成多项式矩阵中的g1(D)都含有常数项1,原因是卷积编码器的输出与此时输入到编码器的信息元相关。由式(4)可知,hn-1(D)也含有常数项,即h0(n-1)=1,将式(3)中的常数项部分移至方程的右边,如下: (7) 其次,将系数矩阵分成两部分,一部分进行Walsh-Hadamard变换,一部分进行遍历,具体如下: 1)将系数矩阵分解成前后两部分:R=[R1R2],R1是(N+1)×r1维矩阵,R2是(N+1)×r2维矩阵,则r1+r2=(d+1)×n-1。R2为参加Walsh-Hadamard的部分,一般r2的取值在16~24之间比较合适。 2)设置循环I=0,1,…,2r1。将每个固定的I转化为r1维二进制向量,将该二进制向量与矩阵R1的每个行向量进行模二加,模二加后的值为“0”或“1”,再将该值取相反数后与式(7)等号右边向量对应行的值相加。 3)作状态统计,R2的行向量维数为1×r2,r2个任意的“0”和“1”组合作为状态,共2r2-1个状态,R2的每个行向量都是其中一个状态,式(7)等号右边向量对应行的值作为该状态的输出,相同状态的输出值进行累加,不存在的状态输出值为0,得到一个(2r2-1)×1维向量。 4)对上述结果进行Walsh-Hadamard变换,得到的结果中,大于设定阈值的数所对应的坐标向量与此时的I的二进制向量的组合即为校验矩阵的系数向量。 2.3生成矩阵估计 上述的识别方法中,还需讨论G(D)和P的遍历范围。在实际应用中,使用的都是性质优越的删除卷积码,则其必然满足如下条件[7]: 1)为了保证删除卷积码Cp能够唯一译码,源卷积码的生成多项式矩阵G(D)必须为基本编码矩阵,即G(0)是满秩。 2)为了克服Ι类无限误差传播,G(D)应当满足有一个前馈逆的条件: 4)删除模式P不能将源码C的任意t时刻输出的整个码字全删除,即P满足(P(i),P(i+1),P(i+2))≠(0,0,0),i=1,…,2n-4。 3.1接入实际卫星链路的实验平台构成 实验平台由AV1443矢量信号发生器、AV3925电磁信号监测分析仪、DMD20通用调制解调器、PCI-1714U采集卡和计算机构成。其中,AV1443矢量信号发生器用来产生自定义的卫星通信信号,PCI-1714U采集卡用来采集解调后的数据,AV3925电磁信号监测分析仪用来检测并分析信号,计算机用于编码分析和对各仪器的监控。实验平台的总体构成如图1所示。 图1 卫星通信编码识别实验平台构成 3.2实验方法与步骤 1)数据产生 按照卫星通信通常采用的CCSDS标准编写删除卷积码基带数据,编码参数如表1所示[9]。 2)数据载入 将传输数据转换成十六进制并加载至AV1443矢量信号发生器。 3)信号发射 设置发射信号的参数,包括载波频率、信号电平、码元速率和调制方式。将此信号通过上变频器变换成射频信号,接入实际链路,使其直接发射到卫星转发器。 表1 CCSDS标准删除卷积码编码参数 4)信号接收 ①通过低噪声放大器直接接收实际卫星转发器的下行信号;②利用AV3925电磁信号监测分析仪进行信号参数估计和调制识别; ③按照识别的参数对DMD20解调器进行设置;④调节发送信号的电平以改变信噪比;⑤通过PCI1714采集解调后的数据。 5)删除卷积码识别 对采集后的码元数据按照文中所述方法进行删除卷积码识别。 3.3实验结果与结论 设置信号样式和信号参数:调制方式为QPSK,码元速率为768Kbps,载波频率为1238.645MHz,将信噪比调节到5dB,此时误比特率约为0.0127。 下面分别从两个方面进行实验,说明文中方法的优势。 在不同信噪比条件下,分别对以上三组删除卷积码进行识别实验,得到能成功识别所需的误比特率分别为0.0228、0.0127、0.008,文献[6]中的试凑法和错误位置穷举法等删除卷积码识别方法均要求误比特率小于0.005,与现有方法相比,本文方法具有更好的误比特率适应性,能够在较高误比特率条件下识别删除卷积码。 Walsh-Hadamard变换法在计算机中需要的最小内存为2r,实验平台中计算机的硬件配置为Intel(R) Core(TM)2 Quad CPU、3G内存,操作系统为32位WINDOWS XP,实验中发现r能达到的最大值为24,对于CCSDS标准的删除卷积码,d=6,因此要求n必须不大于3。改进Walsh-Hadamard变换法将一部分系数矩阵用来遍历,如果不考虑实时性要求,理论上对r值没有限制,能够识别更高码率的删除卷积码。 在误码情况下,本文根据校验矩阵的特点,对校验矩阵方程组进行变形,提出了改进Walsh-Hadamard变换的删除卷积码方法,该方法可以在较高误比特率情况下识别CCSDS标准的删除卷积码,并且能够适应高码率的删除卷积码。最后通过真实卫星链路构建了卫星链路编码识别实验平台,验证了本文方法的有效性。■ [1]邹艳,陆佩忠.关键方程的新推广[J].计算机学报,2006,29(5):712-718. [2]刘杰,张立民,兰天.卷积码盲识别技术研究[J].航天电子对抗,2014,30(4):26-29. [3]Wang Fenghua, Huang Zhitao, Zhou Yiyu. A method for blind recognition of convolution code based Euclidean algorithm[C]∥International Conference on Wireless Communications. Shanghai: IEEE Press,2007: 1414-1417. [4]刘健,王晓君,周希元.基于Walsh-Hadamard变换的卷积码识别[J].电子与信息学报,2010,32(4) :884-888. [5]Lu Peizhong, Shen Li, Luo Xiangyang. Blind recognition of punctured convolutional codes[C]∥International Symposium on Information Theory. Shanghai: IEEE Press, 2004:457. [6]陆佩忠,沈利,邹艳,等.删除卷积码的盲识别[J].中国科学E辑(信息科学),2005,35(2):173-185. [7]Proakis JG. 数字通信[M].北京:电子工业出版社,2006. [8]游凌,朱中梁.Walsh函数在解二元域方程组上的应用[J].信号处理,2000,16(12):27-30. [9]CCSDS 131.0-B-1—2003 TM synchronization and channel coding[S]. Washington, DC, USA,2003. The recognition method for CCSDS punctured convolution code Hu Yihua1,2, Xu Jianhua3, Wang Lei1,2, Xiang Changbo3 (1.State Key Laboratory of Pulsed Power Laser Technology, Electronic Engineering Institute,Hefei 230037,Anhui,China;2.Anhui Province Key Laboratory of Electronic Restriction,Hefei 230037, Anhui, China;3.The 41stInstitute of China Electronics Technology Group Corporation, Qingdao 266555, Shandong,China) The definition of punctured convolution code is introduced. The math model of punctured convolution code recognition is established according to relationship between punctured convolution code and source convolution code. The improvement Walsh-Hadamard method is presented to overcome the increasing operation and data quantity problem of Walsh-Hadamard transform in punctured convolution code recognition. The generator matrix and check matrix of punctured convolution code can be recognized effectively by this method. The experiment platform for punctured convolution code recognition is built by real satellite link. punctured convolution code;generator matrix;check matrix;recognition;experiment platform 2016-05-16;2016-07-04修回。 胡以华(1962-),男,教授,博士生导师,研究方向为信息获取与控制技术。 TN975;TN927+.2 A
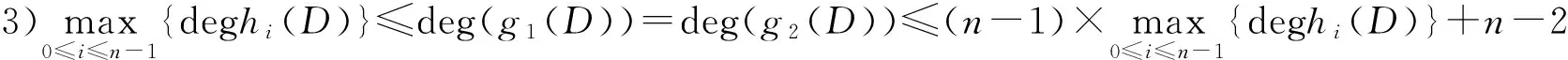
3 星地实际链路识别实验

4 结束语

