复杂电磁环境下组网雷达对隐身目标的跟踪研究*

李修和，冉金和

(电子工程学院，安徽 合肥 230037)



复杂电磁环境下组网雷达对隐身目标的跟踪研究*

李修和，冉金和

(电子工程学院，安徽 合肥 230037)

在复杂电磁环境背景下，研究了组网雷达基于粒子滤波算法对隐身目标的跟踪滤波问题，建立了雷达观测方程和隐身目标的多基地雷达截面积模型，分析了基于UPF的组网雷达目标跟踪滤波算法。利用计算机仿真验证了复杂电磁环境下组网雷达利用粒子滤波技术跟踪隐身目标的有效性，并对几种跟踪算法的效率进行了比较。

组网雷达；目标跟踪；粒子滤波；仿真

0　引言

信息技术的迅猛发展和其在军事领域的广泛运用，加之对抗双方围绕电磁频谱控制权的争夺使得战场电磁环境日趋复杂。战场空间己方电子设备的密集部署等因素引起的电磁影响和己方电子干扰等形成的电磁威胁，是战场复杂电磁环境的主要构成因素。组网雷达通过将多部不同体制、不同频段、不同程式(工作模式)、不同极化方式的雷达或者无源侦察装备适当布站，借助通信手段链接成一个有机整体。作为一种四抗能力(抗电子干扰、抗反辐射摧毁、抗隐身和抗低空突防)较强的新体制雷达，组网雷达对抗隐身目标具有单基或单部雷达无法比拟的优势。

本文就复杂电磁环境下组网雷达对隐身目标的跟踪问题进行研究，主要考虑目前存在的两个现实局限情况：一是目前多目标跟踪技术大多侧重于常规杂波环境，没有考虑实际的战场环境对观测信息的影响；二是复杂电磁环境引起的非线性和非高斯问题异常严重，常用的扩展卡尔曼滤波(EKF)、去偏转换卡尔曼滤波(DCMKF)、无味卡尔曼滤波(UKF)等算法在实际应用中都存在较大缺陷。近年来，随着计算能力以及统计理论的发展，粒子滤波(PF)算法得到了迅速的发展，在处理非线性非高斯问题中显示了强大的生命力。粒子滤波算法虽然比较简单，但在采样过程中有时会出现比较严重的退化现象。UPF是粒子滤波器的一种改进算法，它能够很好地解决粒子滤波器的退化现象。本文拟采用UKF和粒子滤波结合的UPF算法，研究复杂电磁环境下组网雷达如何综合利用多个雷达站的观测信息对隐身目标进行目标跟踪。

1　复杂电磁环境下对隐身目标观测方程建模

1.1不同复杂度下雷达观测方程建模

为了建立复杂电磁环境下雷达的具体观测方程，将战场电磁环境的复杂程度等级具体划分为四级：Ⅰ级电磁环境、Ⅱ级电磁环境、Ⅲ级电磁环境和Ⅳ级电磁环境。

1)Ⅰ级电磁环境

Ⅰ级电磁环境即简单电磁环境，雷达站在捕获目标时，基本没有受到电磁威胁。此时利用雷达站全部的测量数据对目标进行定位跟踪，对于三坐标雷达，包括测得的目标斜距ri、方位角φi和俯仰角εi；对于二坐标雷达，包括目标斜距ri、方位角φi，它们的表达式如下：

(1)

写成矩阵形式为：

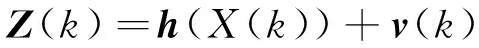
(2)

此时的测量子集是：Z(k)=(ri,φi,εi)T

2)Ⅱ级电磁环境

Ⅱ级电磁环境即轻度电磁环境，雷达站在捕获目标时，受到一定的电磁威胁，但电磁威胁的强度比较弱，此时雷达站仍能观测到全部数据，但由于电磁威胁的影响，测量值偏差比无干扰时明显增大。

根据相关文献，认为Ⅱ级电磁环境的判断条件是雷达接收机端内的信干比满足：

10lgSj>-3dB

(3)

3)Ⅲ级电磁环境

Ⅲ级电磁环境即中度复杂电磁环境，雷达站受到的电磁威胁增大到一定程度后，将无法给出目标的斜距测量数据，三坐标雷达仍能够给出目标的方位角φi和俯仰角εi，二坐标雷达仍能给出目标的方位角φi。同样根据相关文献，Ⅲ级电磁环境的判断条件是：

-40dB<10lgSj≤-3dB

(4)

此时，对雷达站而言，测量的子集为Z(k)=(φi,εi)T或Z(k)=(φi)T，并且有如下的表达式：

(5)

写成矩阵形式，则表达为：

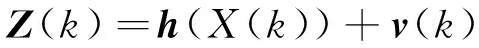
(6)

此时的测量子集是：Z(k)=(φi,εi)T。

4)Ⅳ级电磁环境

Ⅳ级电磁环境即重度复杂电磁环境，雷达站斜距测量数据、方位和俯仰测量数据丢失，该雷达站不提供任何观测信息参与定位。

综上可见，在雷达网中雷达由于受不同干扰强度的干扰，各单站可能参与定位的观测向量有：1)Z(k)=(ri,φi,εi)T；2)Z(k)=(φi,εi)T；3)Z(k)=(φi)T。

1.2隐身目标的多基地雷达截面积(RCS)

组网的雷达采用空间分集的形式，以多发多收的形式存在，当发射机与接收机远离时，使目标在该多站之间运动，并使两个站之间夹角(简称双基地角)β≥130°，这样还可获得目标前向散射信号，这是实现反隐身的关键所在，原因是多基地RCS的增大是由前向散射获得。例如一个球体的投影面积为A、半径为r，被波长为λ的电磁波照射时，其前向散射面积为：

(7)

而该球的单基地雷达后向散射面积为：

(8)

(9)

若r/λ=10，则σf/σb=4000(36dB)。故前向散射面积明显增大。

在基于组网雷达的多基地散射结构中，发射站、目标和接收站构成了一个双基地角，双基地角平分线则往往定义为等效波矢量，当双基地角较小时，等效波矢量可用于更换单基地截面积中的波矢量，以便得出双基地雷达RCS的较佳近似值。但是当双基地角较大时(180°≥β≥130°)，就不能用这种近似方法了。其理由如下：1)由于入射方向波矢量决定了散射体的照射与投影区域，故电流积分区域(使用物理理论的情况下)，如用等效波矢量，则可能是极为错误的。2)使用高频渐进技术必须极其谨慎，这是由于等效波矢量的大小随双站角度的增大而减小。波数的依次减小意味着目前来自散射体的响应要比局部集中散射更加扩展。3)现有的投影法与发射机和接收机有关。对发射机和接收机，因为往往不是所需要的，所以不能简单地应用同一投影过程。

对于形状复杂的物体，通过分析得出了双基地雷达截面积σb与单基地雷达截面积σm的经验公式：

(10)

式中，n为经验参数，一般取n为7～10；β为双基地角，单位是弧度。

从式(10)可以看出，双基地雷达的RCS总是大于单基地雷达的RCS。当目标位于低空时，双基地角可以满足180°≥β≥130°的条件，从而获得较大的RCS。

而对于隐身目标，在计算其单基地雷达的RCS时，考虑机翼是主要的镜面散射体，它的RCS值最大,但其大后掠角却使雷达设计者最关心的飞机迎头方向的RCS显著减小。当雷达以小仰角观测迎面飞来的飞机时，机翼的前沿可被近似看作一段圆柱体，法线方向照射时，单侧机翼RCS的方向图为：

(11)

式中，λ为雷达波长,D为直径(对应翼厚),L为柱体长(对应翼长),θ为偏离机翼法线的角度。机翼后掠角为φ，飞机的方位角为α。

2　复杂电磁环境下基于UPF的组网雷达目标跟踪滤波算法研究

复杂电磁环境下，如组网雷达中网内大部分雷达受到压制性干扰，单站雷达的距离信息就会丧失，无法在单站对目标进行定位滤波而形成航迹，此时就不能够应用分布式航迹融合方式，组网雷达将被迫采取传送单站观测信息到融合中心进行处理的方式，结合多个雷达的信息来对目标进行滤波跟踪。近年来有很多文献对组网雷达目标跟踪进行了研究，但大都假定了所有传感器同步采样，或者没有通信延迟。实际上，传感器常常是异步工作，而且采样速率不等，通信延迟不同。因此，在非线性非高斯环境，组网雷达系统中部分传感器受到干扰而测量信息不全，且组网雷达异步工作时，如何充分利用“残留”的信息对目标进行融合跟踪，是非常必要且十分重要的问题。

2.1量测数据的串行合成

组网雷达系统中各传感器异步扫描，每次扫描周期结束时，将此次扫描的观测量附带时间送到中心进行处理。

以两部雷达为例，设雷达1和雷达2的扫描周期都为T，但两者不同步，测量集合D1={Z1(k)|k=1,2,…}和D2={Z2(k)|k=1′,2′,…}，采样时间之间的关系如图1所示。

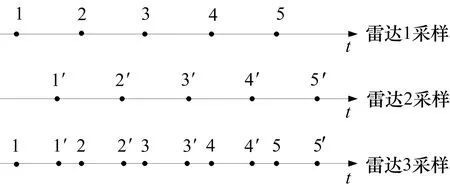
图1　集中式雷达数据流合成图

对合成序列{Z(l)|l=1,1′,2,2′,…}，实际上存在2个采样周期T1、T2，且有T=T1+T2。推广到多雷达情形，为不失一般性，设组网雷达由m部采样周期相同的异步工作的雷达组成，对同一目标的测量集合分别为Di={Zi(k)|k=1,2,…;i=0,1,2,m-1}，则对合成的观测序列有：

(12)

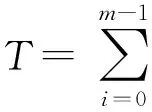
2.2UKF和粒子滤波结合的UPF算法

对经过量测合成之后的测量数据，本文采用UPF算法对其进行滤波处理。粒子滤波不受非线性、非高斯滤波问题的限制，因而得到了广泛的应用。粒子滤波中的一个关键是提议分布。目前，有许多不同的提议分布，最常见的方法是直接采用先验概率密度函数作为重要密度函数。这种做法直观而且易于实现，缺点是没有考虑使用新的观测值，因而具有一定盲目性，导致最终滤波效果一般。

有的学者提出用扩展的卡尔曼滤波来产生重要性概率密度函数。尽管基于EKF的粒子滤波方法在估计性能上有所改善，但由于EKF在模型线性化和高斯假设中引入了过多的误差，其改进效果不是很明显。因此本文采用一种新的粒子滤波器即UPF，该方法使用UKF产生重要性密度，其算法主要步骤如下：

1) 初始化(k=0)。根据初始均值和协方差均匀抽取N个粒子。

2) 在每个采样时刻，对所有的粒子，UKF更新每个粒子的每个Sigma点。在UKF算法中，由于具有噪声项，需要对状态进行扩维处理。

①对每一个粒子进行Sigma点采样，本文使用比例对称采样方法。

(13)

式中，γ=(n+λ)1/2，λ=α2(n+k)-n。

(14)

(15)

②预测方程：

(17)

(18)

(19)

(20)

(21)

(22)

③更新方程：

(23)

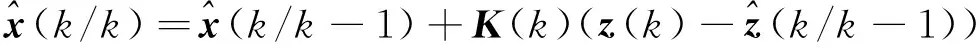
(24)

(25)

④使用UKF估计的均值和方差作为PF计算权值的提议分布。

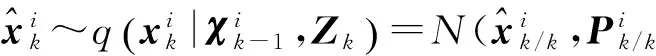
(26)

复杂电磁环境下，观测噪声为非正态分布，要代入相应的概率密度函数(即测量噪声的概率密度函数)进行计算。

对所有粒子计算其权值，并进行归一化。

⑤输出k时刻的状态估计。

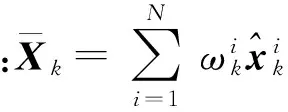
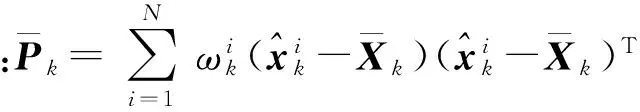
3) 重采样。

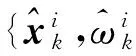
(27)

4)递归。

返回步骤2)，并令k=k+1。

3　计算机仿真

3.1仿真场景和条件设置

在仿真中设置如下场景：组网雷达由3个三坐标跟踪雷达组成，以融合中心为坐标原点建立坐标系，如图2所示。其中雷达2(30km,0,0)为厘米波雷达，雷达1(-15km,30km,0)和雷达3(-15km,-30km,0)为分米波雷达，干扰为远距离支援干扰且干扰机的工作频段为10GHz左右，这里我们考虑较强干扰情况，雷达2距离信息丢失，但可以观测到方位信息。各雷达每次扫描周期结束时，将此次扫描观测量附带时间送到中心进行处理。三传感器异步采样，取样时间间隔相差3s，采样周期取为9s，观测点数为100。假设目标的初始位置为(80km,0,20km)，初始速度为(-0.1km/s,0,0)。本文对EKF、PF、UPF进行仿真，PF中粒子数目为3000，进行500次蒙特卡罗仿真实验。

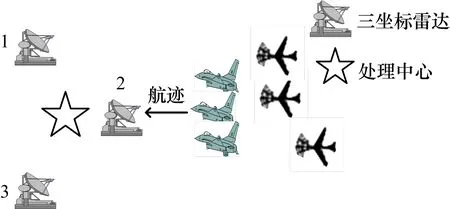
图2　组网雷达目标跟踪态势图

3.2仿真结果与分析

图3～5给出了EKF、PF和UPF在观测噪声为闪烁噪声(ε=0.2)情况下目标运动的跟踪轨迹。图6～7给出了三种方法估计下的x方向和z方向的均方根误差。

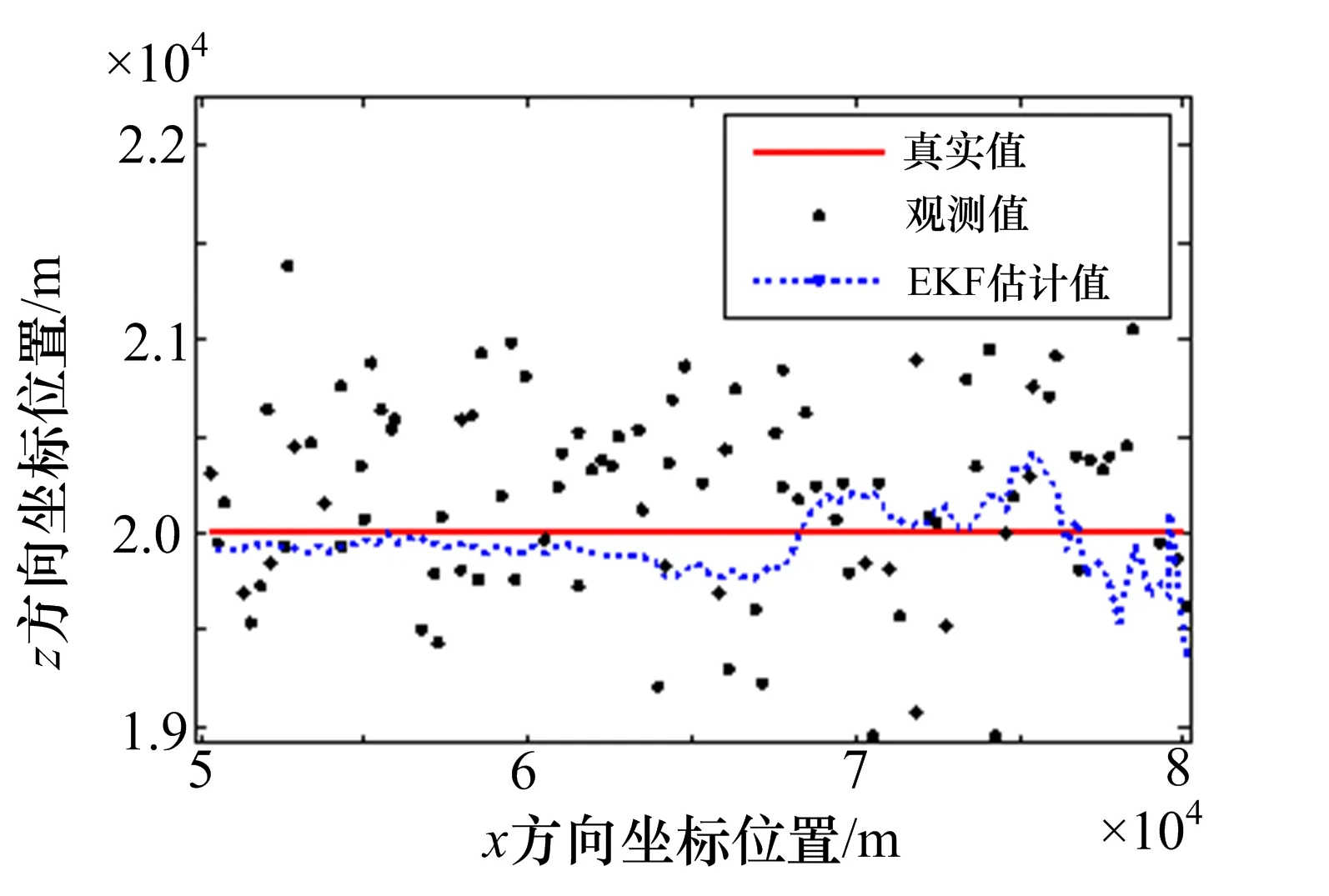
图3　EKF跟踪轨迹(ε=0.2)

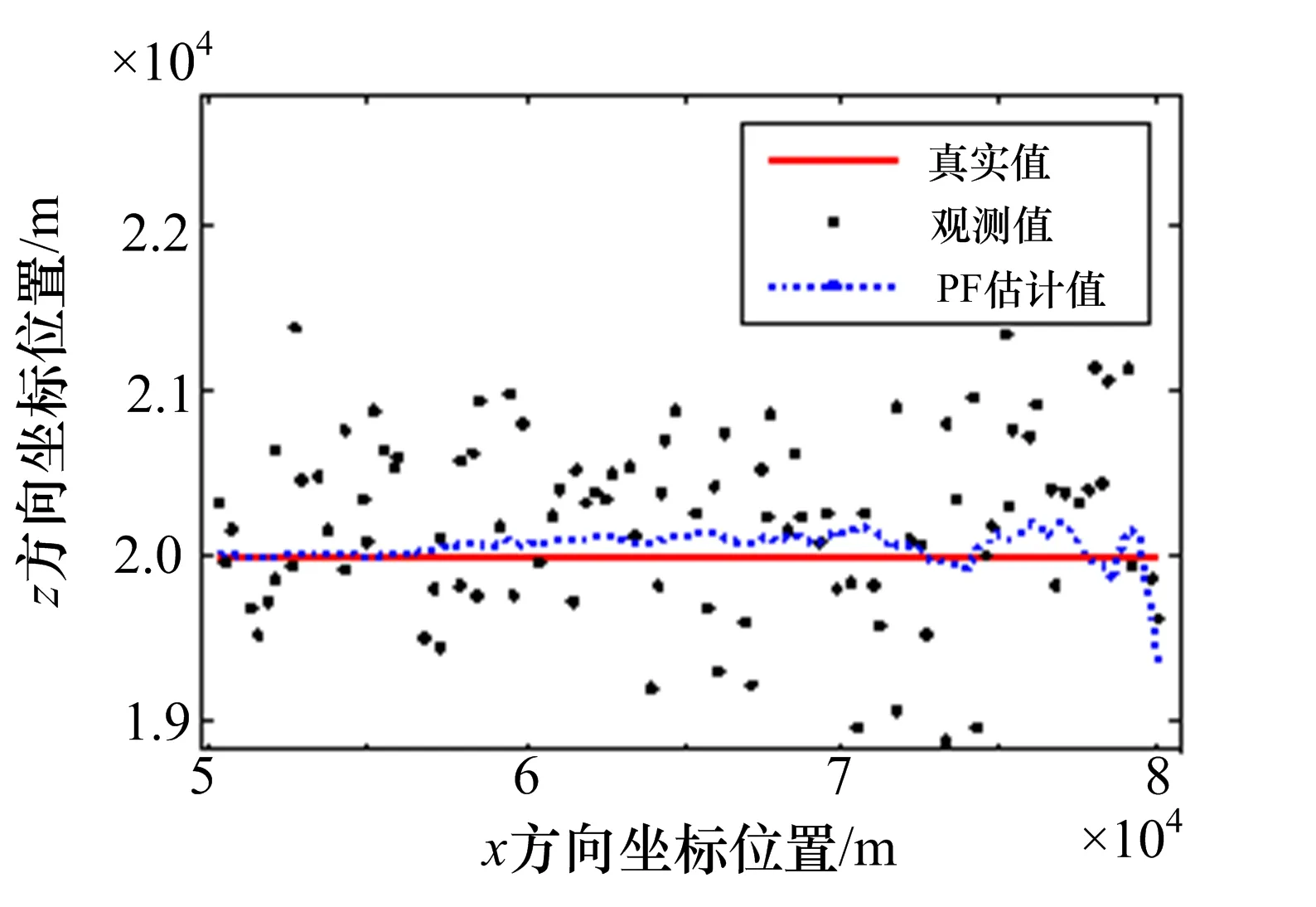
图4　PF跟踪轨迹(ε=0.2)

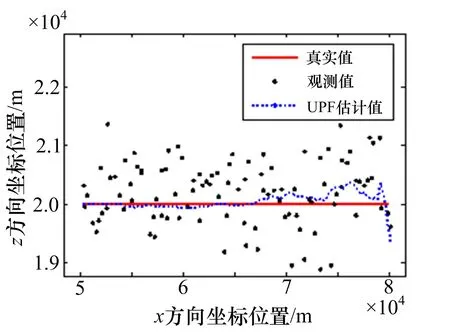
图5　UPF跟踪轨迹(ε=0.2)

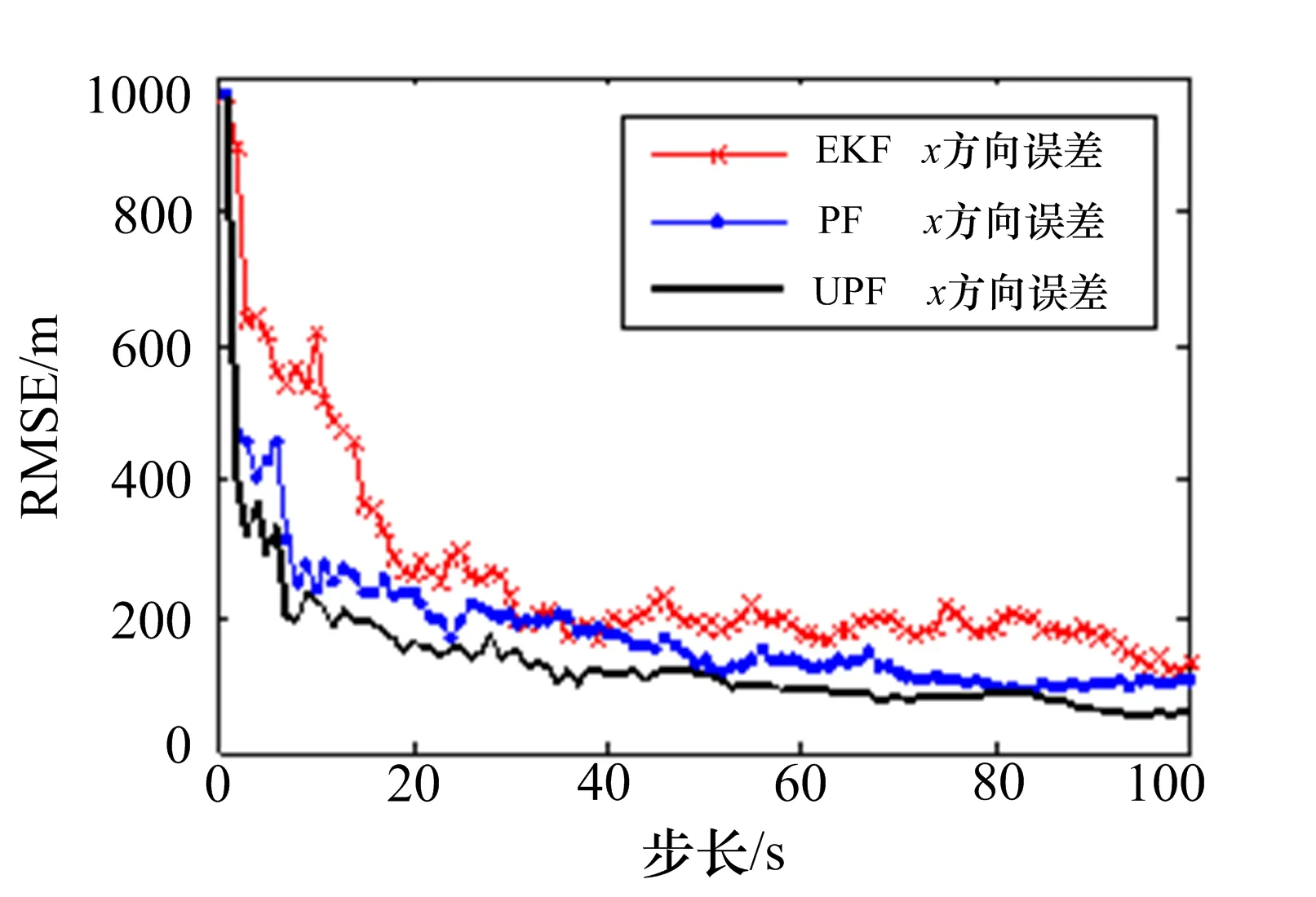
图6　x方向位置均方根误差(ε=0.2)

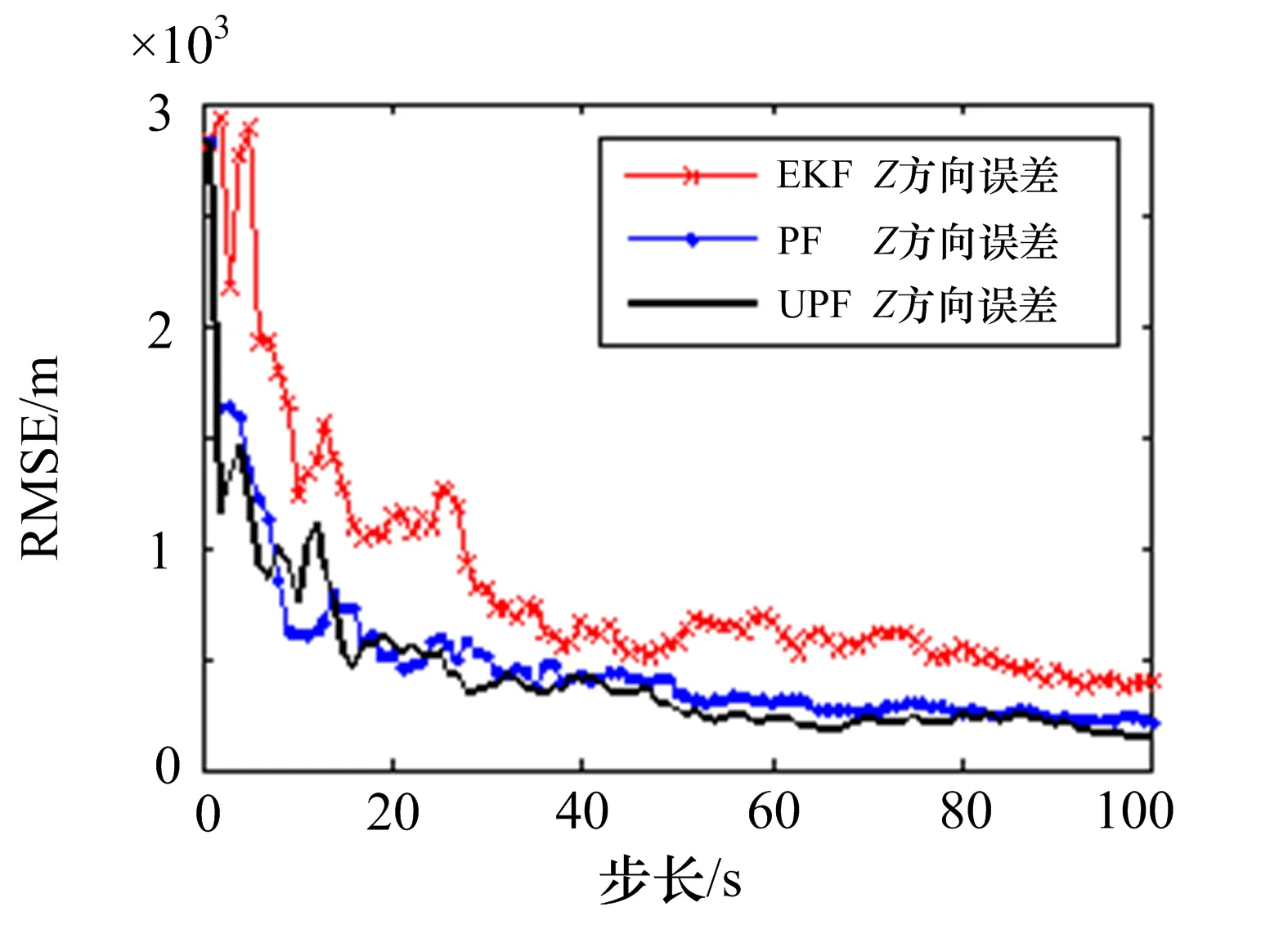
图7　z方向位置均方根误差(ε=0.2)

通过分析仿真结果，可以得到如下结论：

1)在复杂电磁环境下，即使是部分雷达受到严重干扰，组网雷达由于空间的分集，也可利用目标的前向散射和量测合成方法， 各站将每次扫描观测量附带时间送到中心进行处理，组网雷达可以对抗隐身目标。

2)在闪烁噪声闪烁强度弱的情况下，组网雷达利用EKF、PF和UPF三种方法均能有效对目标进行跟踪，随着闪烁强度的增大，闪烁噪声概率密度函数同高斯函数差别变大，因此，采用矩匹配的EKF算法误差明显变大。PF和UPF算法随闪烁强度的增大而误差变化不大。

3)在复杂电磁环境下，系统表现为非线性非高斯，UPF粒子滤波器由于在产生预测粒子时利用了最新的观测数据，因此对状态的估计精度要高于标准的粒子滤波器的精度。同时，UPF可以极大地减少PF所用的粒子数，大大缩短了运算时间，与普通的粒子滤波相比，滤波精度和实时性也有很大的提高。

4　结束语

随着新军事变革的推进，防空系统中的目标反隐身问题已经成为一道亟待解决的难题。组网雷达在反隐身问题上由于体制上的优越性，受到各国的高度重视。本文利用UKF和粒子滤波结合的UPF算法，研究组网雷达综合利用多个雷达站的观测信息对隐身目标进行目标跟踪的问题，希望能引起相关学术界同行的共鸣，有许多战场复杂电磁环境下多传感器数据融合技术的应用和实践问题值得深入开展研究。■

[1]陈永光, 李修和. 组网雷达作战能力分析与评估[M].北京：国防工业出版社, 2006.

[2]孙仲康, 周一宇, 何黎星. 单站无源跟踪技术[M].北京：国防工业出版社, 2008.

[3]李修和. 战场电磁环境建模与仿真[M].北京：国防工业出版社, 2014.

[4]胡来招. 无源定位[M].北京：国防工业出版社, 2004.

[5]韩崇昭, 朱洪艳. 多源信息融合[M].北京：清华大学出版社, 2006.

[6]Chrzanowski EJ. Radar active countermeasures[M].Artech House, Inc., 1990.

[7]杨振起, 张永顺, 骆永军. 双(多)基地雷达系统[M].北京：国防工业出版社, 1998.

Research on tracking stealth targets of netted radar in complex electromagnetic environment

Li Xiuhe, Ran Jinhe

(Electronic Engineering Institute, Hefei 230037, Anhui, China)

The problem of netted radar tracking stealth targets based on particle filtering in complex electromagnetic environment is studied. The radar observation equations and the radar cross section of stealth targets in complex electromagnetic environment are established. The tracking algorithm based on unscented Kalman filter of netted radar is analyzed. Simulation results validate the particle filtering technology of netted radar can track stealth targets in complex electromagnetic environment, and some conclusions on the efficiency of tracking algorithms are drawn.

netted radar;target tracking;particle filtering;simulation

武器装备预研重点基金项目 (9140A33020112JB39085)

2016-06-10；2016-07-11修回。

李修和(1975-)，男，教授，博士，研究方向为战场电磁环境基础与应用、信息作战模拟与仿真及多源信息融合技术等。

TN971;TN974

A