非线性微分方程三阶三点边值问题两个正解的存在性

郭丽君

(兰州交通大学博文学院，甘肃 兰州　730101)



非线性微分方程三阶三点边值问题两个正解的存在性

郭丽君

(兰州交通大学博文学院，甘肃 兰州730101)

考虑以下三阶三点边值问题：u‴(t)+a(t)f(u(t))=0，t∈(0，1)；u(0)=u″(0)=0，u′(1)-αu(η)=λ，其中0<η<1，0<α<1/η，λ∈(0，),通过建立相关线性边值问题的格林函数得到解的形式，运用不动点指数理论建立了上述边值问题至少两个正解的存在性准则.

三阶三点边值问题；正解；存在性；锥；格林函数；不动点指数理论

【引用格式】郭丽君.非线性微分方程三阶三点边值问题两个正解的存在性[J].北华大学学报(自然科学版)，2016，17(5)：566-571.

1　引　　言

近年来，微分方程三阶三点边值问题受到了广泛的关注[1-13]，所用的方法有各类不动点定理：文献[1-2]运用了Leggett-Williams不动点定理，文献[3-5]运用了Guo-Krasnoselskii不动点定理，文献[6-8]运用了Leray-Schauder不动点定理，文献[9]运用了Avery-Henderson不动点定理，文献[10]运用了Avery-Peterson不动点定理.本文运用不动点指数理论研究了下列边值问题至少有两个正解的存在性准则：

其中0<η<1，0<α<1/η，λ∈(0，).

文献[1]讨论了当边值问题(1)-(2)中参数λ=0时的特殊情况，但在文献[1]及文献[2-7，9-10]中相关的格林函数形式较复杂，没有得到更好的性质.本文的目的是进一步研究当参数λ>0时的边值问题(1)-(2)，构造了新的格林函数，且形式上较简单，得到了新的性质，通过运用不动点指数定理，在非线性项f满足一定条件的情况下得到了边值问题(1)-(2)至少两个正解的存在性准则.

假设以下条件始终成立：

(C1)f∈C([0，+)，[0，+))；

(C2)a∈C([0，1]，[0，+))且在[τ，1]上a(t)不恒为零，其中τ为(0，1)上任意常数.

2　预备引理

引理1设0<α<1/η，则对任意给定的y∈C[0，1]，边值问题

(5)

称为Green函数.

证明：事实上，如果u(t)是边值问题(3)-(4)的解，则可令

由u(0)=u″(0)=0，可得A=C=0.再由u′(1)-αu(η)=λ，可得

因此，边值问题(3)-(4)有唯一解

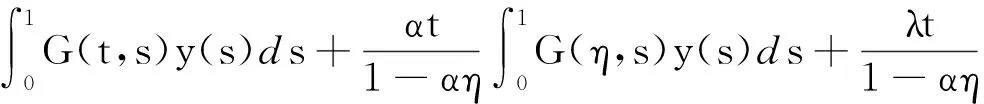
证毕.

对本文格林函数(5)，有如下两个引理.

引理2对任意(t，s)∈[0，1]×[0，1]，有0≤G(t，s)≤1-s.

证明：首先考虑0≤s≤t的情况.此时

如果t≤s≤1，则有

0≤G(t，s)=t(1-s)≤1-s.

因此

0≤G(t，s)≤1-s，(t，s)∈[0，1]×[0，1].

证毕.

证明：如果0≤s≤t，则有

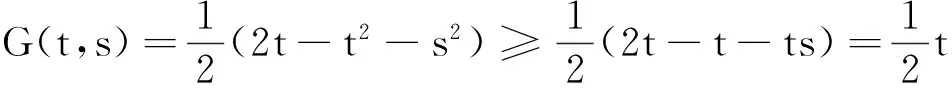
如果t≤s≤1，则有

因此，对任意(t，s)∈[0，1]×[0，1]，均有

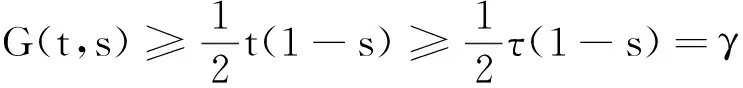
证毕.

3　主要结果

以下假定0<α<1/η，参数λ>0且条件(C1)和(C2)满足.记

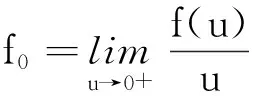
定理2假设下述条件成立：

(a) f0=f=0；

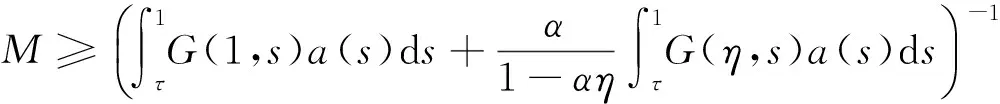
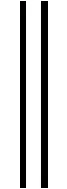
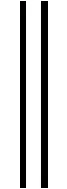
显然K⊂E是锥.对u∈K，t∈[0，1]定义

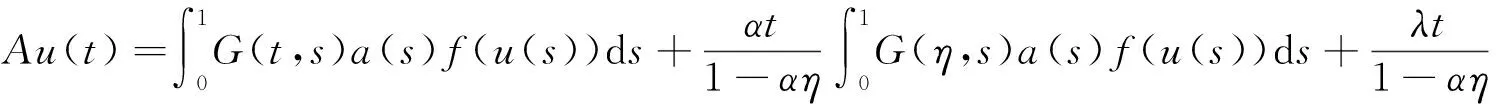
由引理2可知，对任意t∈[0，1]，都有

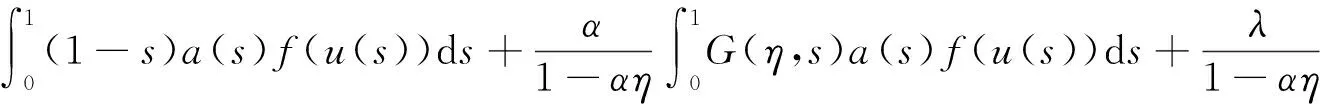
故

(6)

由引理3和式(6)可得，当t∈[τ，1]时有

首先，由于f0=0，故存在00且满足

(7)

从而

故由定理1的(ⅰ)可知

i(A，ΩH1，K)=1.

(8)

其次，由于f=0，故存在，使得当时， f(u)≤μu,其中μ>0满足

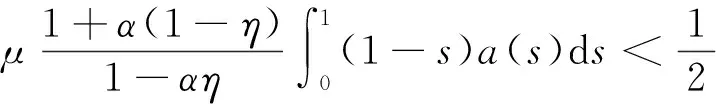
(9)

下面分两种情形考虑：

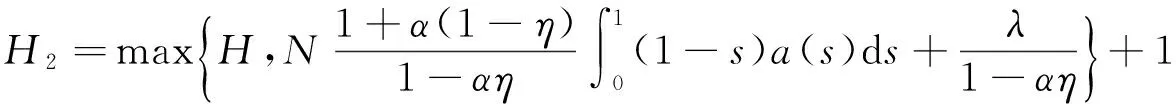
f(u)≤f(H2)，0≤u≤H2.

(10)

i(A，ΩH2，K)=1.

(11)

从而

故由定理1的(ⅱ)可知

i(A，ΩH，K)=0.

(12)

由式(8)，(11)，(12)以及不动点指数的可加性可得

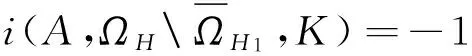
证毕.

[1] SUN J P，GUO L J，PENG J G.Multiple nondecreasing positive solutions for a singular third order three point bvp[J].Communications in Applied Analysis，2008，12： 91-100.

[2] 吴红萍.一类非线性三阶三点边值问题的多个正解[J].贵州大学学报(自然科学版)，2014，31(2)：4-6.

[3] 孙建平，张小丽.非线性三阶三点边值问题正解的存在性[J].西北师范大学学报(自然科学版)，2012，48(3)： 29-31.

[4] GUO L J，SUN J P，ZHAO Y H.Existence of positive solution for nonlinear third-order three-point boundary value problem[J].Nonlinear Analysis，2008，68： 3151-3158.

[5] 孙建平，曹珂.一类非线性三阶三点边值问题正解的存在性[J].兰州理工大学学报(自然科学版)，2010，36(2)： 123-124.

[6] 吕学哲，裴明鹤.一类三阶三点边值问题正解的存在性[J].北华大学学报(自然科学版)，2014，15(5)： 577-580.

[7] 白婧，李永祥.含一阶导数项的三阶周期边值问题解的存在唯一性[J].四川师范大学学报(自然科学版)，2015，38(6)： 834-837.

[8] 姚志健.非线性三点边值问题正解的新的存在性定理[J].数学杂志，2014，34(1)： 173-178.

[9] 张立新，孙博，张洪.三阶三点边值问题的两个正解的存在性[J].西南师范大学学报(自然科学版)，2013，38(10)： 30-33.

[10] 张立新.三阶边值问题的3个正解的存在性[J].四川师范大学学报(自然科学版)，2011，34(4)： 466-470.

[11] 裴明鹤.三阶非线性常微分方程两点与三点边值问题解的存在性与惟一性[J].北华大学学报(自然科学版)，2003,4(1):5-11.

[12] 沈建和，余赞平，周哲彦.非线性三阶常微分方程的非线性三点边值问题解的存在性[J].纯粹数学与应用数学，2007,23(3):355-360,365.

[13] 高永馨，汪凤琴.三阶非线性微分方程三点边值问题解的存在性[J].黑龙江大学自然科学学报，2015,32(4)：421-427.

[14] GUO D，Lakshmikantham V.Nonlinear problems in abstract cones[M].New York： Academic Press，1988.

【责任编辑：伍林】

Existence of Two Positive Solutions for Third-Order Three-PointBoundaryValueProblemsofNonlinearDifferentialEquations

Guo Lijun

(Bowen College of Lanzhou Jiaotong University,Lanzhou 730101，China)

Weconcernedwiththefollowingthird-orderthree-pointboundaryvalueproblem

third-orderthree-pointboundaryvalueproblem；positivesolution；existence；cone；Greenfunction；fixedpointindextheorem

1009-4822(2016)05-0566-06

10.11713/j.issn.1009-4822.2016.05.002

2016-05-30

甘肃省高等学校科研项目教育厅立项(项目编号：2015B-214).

郭丽君(1980-)，女，讲师，主要从事非线性分析研究，E-mail：5148806@qq.com.

O175.8

A

where0<η<1，0<α<1/η，λ∈(0，)isaparameter.ByestablishingGreenfunctionfortheassociatedlinearboundaryvalueproblem，thesolutionfortheaboveboundaryvalueproblemisobtained.Thentheexistencecriterionofatleasttwopositivesolutionsfortheaboveboundaryvalueproblemisobtainedbyusingfixedpointindextheorem.